Prove that if the figure S is bounded by a simple convex contour and is situated between the ordinates y1andy2, then the volume of the solid generated by revolving this figure about the x-axis can be expressed by the formula
V=2π∫y2y1yhdy,
where h=x2(y)−x1(y),x=x1(y) being the equation of the left portion of the contour and x=x2(y) that of the right portion.
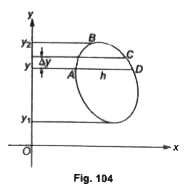
The correct Answer is:V=2π∫y2y1yhdy
Topper's Solved these Questions
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Pressure, Work and Other Physical Quantities by the Definite Integrals7videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity15videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Area of Surface of Revolution10videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS9videos
APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONS
- BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS5videos
BASIC CLASSES OF INTEGRABLE FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The volume of solid generated by revolving about the y-axis the figure bounded by the parabola y=x2andx=y2 is
A215πB245πC215πD524π
Compute the volume of the solid generated by revolving about the x-axis the figure bounded by the parabola y=0.25x2+2 and the straight line 5x−8y+14=0
View SolutionFind the volume of the solid generated by revolving, about the x-axis, the infinite branch of the curve y=2(1x−1x2)forx≥1.
View SolutionFind the area of the surface generated by revolving about the x-axis a closed contour OABCO formed by the curves y=x2andx=y2
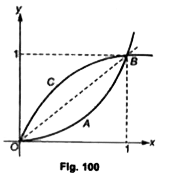 View Solution
View SolutionFind the volume of the solid generated by revolving about the line y=−2a the figure bounded by the parabola y2=4ax and the straight line x=a
 View Solution
View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
View SolutionThe figure bounded by an arc of the sinusoid y= sin x, the axis of ordinates and the straight line y=1 resolves about the y-axis
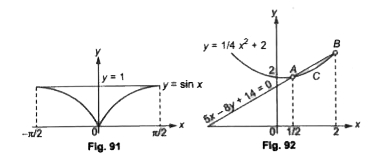
Compute the volume V of the solid of revolution thus generated.View SolutionThe planer region bounded by the parabola y=2x2+3, the x-axis and the verticals x=0 and x=1 revolves about the y-axis. Compute the volume of the solid of revolution thus generated.
View Solution

