Prove the following statement. "The bisector of an angle of a triangle divides the sides opposite to the angle in the ratio of the remaining sides"
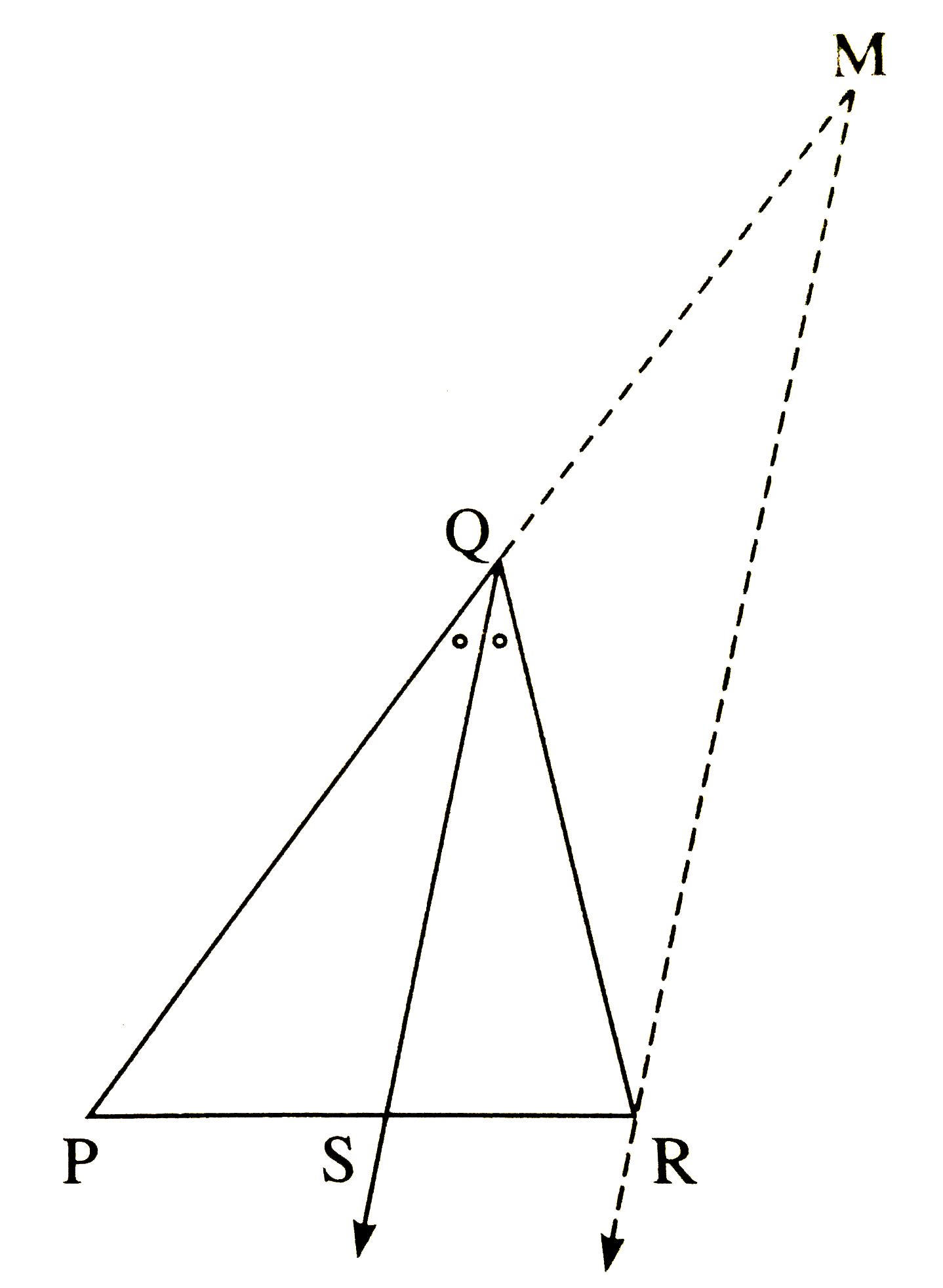
Statement : The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
Given In ΔPQR, bisector of ∠PQR intersects side PR in point S such that P-S-R
To prove : PQQR=PSSR
(12 mark of figure 12 mark for given, to prove and construction)
Construction : Draw a line parallel to ray QS through point R. Extend seg PQ to intersect the line at point M such that P-Q-M.
Proof : In ΔPMR
seg, QS||side MR .....[Construction]
∴ by basic proportionality theorem,
PQQM=PSSR....(1)
Ray QS||side MR and line PM is the transversal
∴∠PQS≅∠QMR...... [Corresponding angles]
Ray QS||side MR and line QR is the transversal.
∴∠SQR≅∠QRM ....[Alternate angles]
∠PQS≅∠SQR
...[Ray QS is the bisector of ∠PQR ...(4)
In ΔQRM
∠QMR≅∠QRM..... [From (2),(3) and (4)]
∴ seg QR ≅ seg QM ,
...[Converse of isosceles triangle theorem]
∴PQQR=PSSR .....[Form (1) and (5)]
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE ANY TWO THE FOLLOWIN SUBQUESTIONS:3videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE THE FOLLOWING SUBQUESTIONS: (ANY ONE)2videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - COMPLETE ANY ONE OUT OF TWO ACTIVITES:2videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - Assignment 8.58videos
MENSURATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTION BASEDEXERCISE - STATISTICS13videos
PRACTICE QUESTION BASED
Similar Questions
In order to prove, 'The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
(i) Draw a neat labelled figure.
(ii) Write 'Given' and 'To prove'.View SolutionThe external angle bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
View Solution
Knowledge Check
- Question 1 - Select One
Read the statemenst carefully and state 'T' for true and 'F' for false .
1. If a line divides any two sides of a triangle in the same ratio , then the line is parallel to the third side of the triangle .
2 . The internal bisector of an angle of a triangle divides the opposite side inernally in the ratio of the sides containing the angle .
3 . If a line through one vertex of a triangle divides the opposite in the ratio of other two sides , then the line bisects the angle at the vertex .
4.Any line parallel to the parallel sides dividesproportionally .
5. Two times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle .A12345TTTTTB12345TTTTFC12345FTFTFD12345TTFTF - Question 2 - Select One
The internal /external bisector of an angled of a triangle divides the opposite side internally / externally in the ratio of the sides containing the angle .
In the given figure ,Ae is the bisector of the exterior ∠CAD meeting BC produced in E . If AB=15 cm , AC = 8 cm and BC =14 cm , find CE .
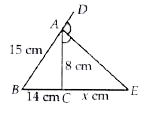 A12 cmB16 cmC20 cmD18 cm
A12 cmB16 cmC20 cmD18 cm - Question 3 - Select One
The side opposite to an obtuse angle of a triangle is :
AsmallestBgreatestChalf of the perimeterDnone of these
The internal angle bisector of an angle of a triangle divide the opposite side internally in the ratio of the sides containgthe angle
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf two angles of a triangle are equal;then sides opposite to them are also equal.
View SolutionIf the angles of a triangle are in the ratio 2:3:7, then the sides opposite to the angles are in the ratio
View SolutionProve that the internal bisector of the angle A of a triangle ABC divides BC in the ratio AB:AC
View Solution

