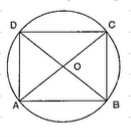
Show that if two chords of a circle bisect one another they must be diameters.
Video Solution
Text Solution
Proof: In △AOC and △BOD
∠AOC=∠BOD
OA=OB
OC=OD
△AOC≅△BOD (By SAS)
Now, AC=BD ____1
In △AOD and △BOC
∠AOD=∠BOC
OA=OB
OC=OD
△AOD≅△BOC (BY SAS)
AD=BC____2
Adding 1 and 2
AC+AD=BC+BD
CAD=CBD
Hence, CD and AB are the diameter of the circle.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogram - Question 2 - Select One
If two chords having lengths a2−1 and 3(a+1), where a is a constant of a circle bisect each other, then the radius of the circle is
A6B15/2C8D19/2
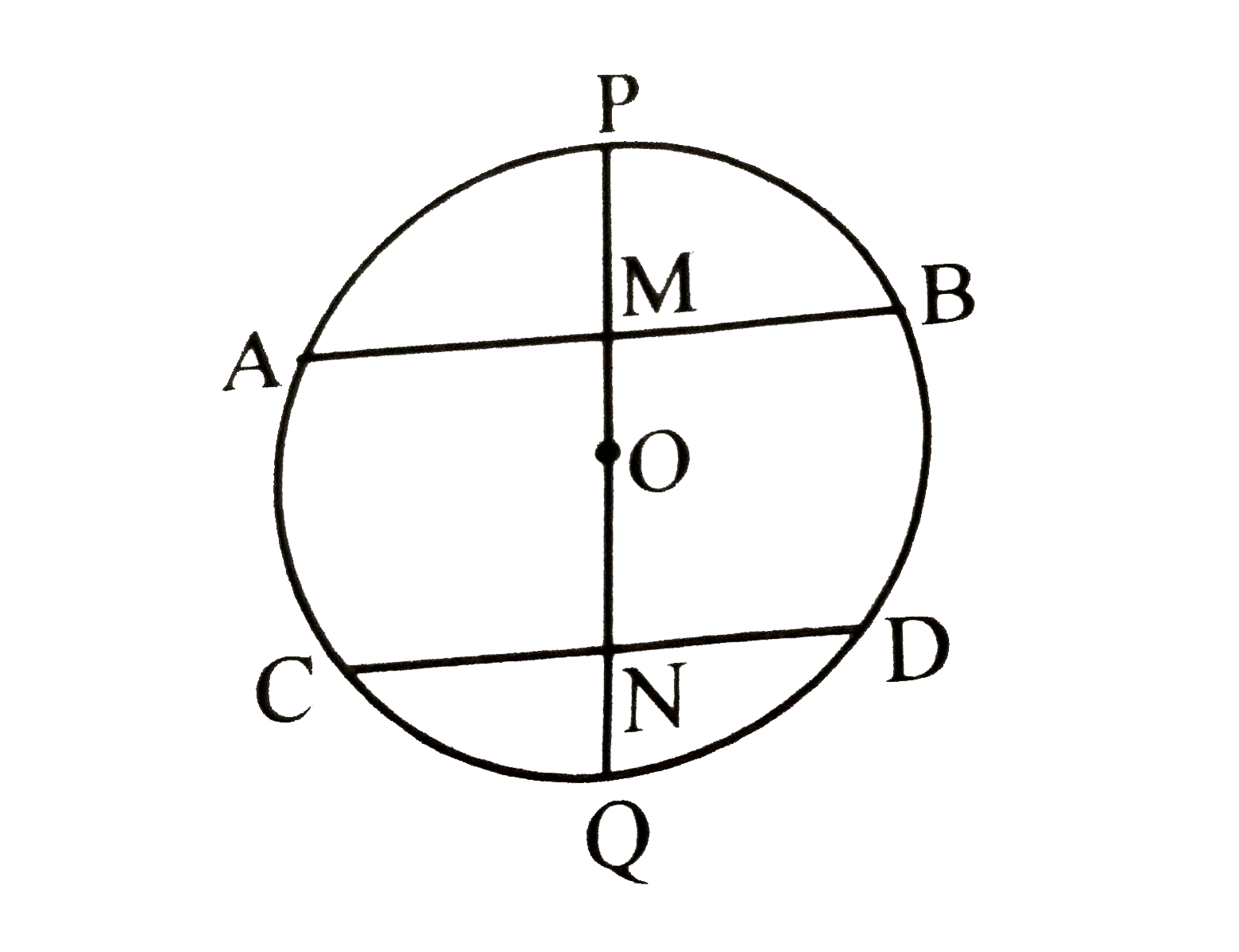
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionProve that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
 View Solution
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters (ii) ABCD is a rectangle
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
View SolutionACandBD are chords of a circle which bisect each other. Prove that (i) ACandBD are diameters (ii) ABCD is a rectangle.
View Solution