Question

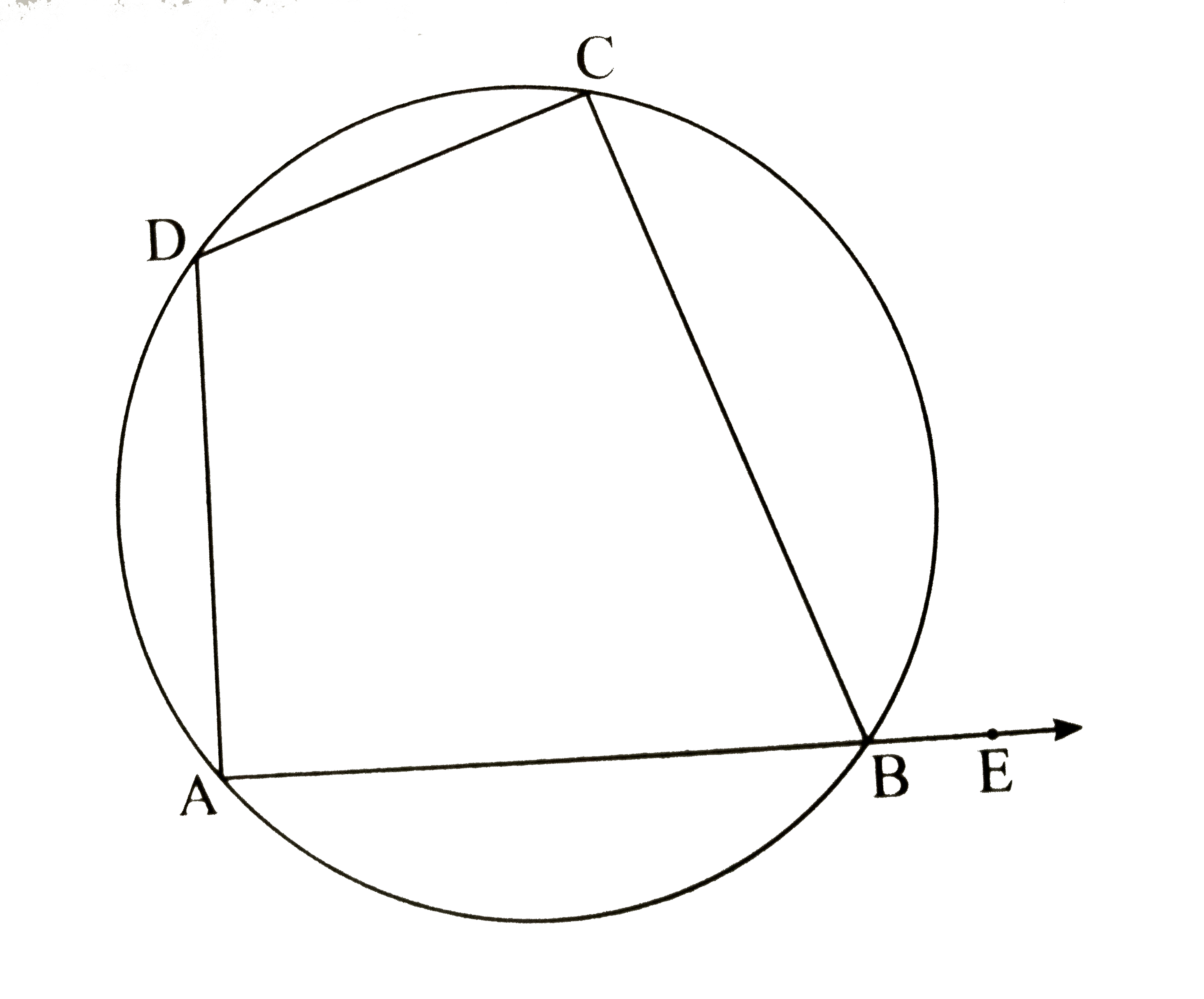
square ABCD is a cyclic quadrilateral in which AB = AD .$\angle BCD={70}^{\circ }$ . Find (i) m (arc BCD) (ii) m (arc BAD) (III) $\angle ADB$

Explanation

To solve the problem step by step, we will find the measures of the arcs BCD and BAD, and the angle ADB in the cyclic quadrilateral ABCD.

Step 1: Understand the Given Information
We have a cyclic quadrilateral ABCD where:
- \( AB = AD \)
- \( \angle BCD = 70^\circ \)

Step 2: Find the Measure of Arc BCD
Using the Inscribed Angle Theorem, we know that the measure of the arc subtended by an inscribed angle is twice the measure of the angle.

1. Since \( \angle BCD = 70^\circ \), the measure of arc BCD can be calculated as:
\( m(\text{arc BCD}) = 2 \times \angle BCD = 2 \times 70^\circ = 140^\circ \)

Step 3: Find the Measure of Arc BAD
To find the measure of arc BAD, we can use the fact that the total measure of the arcs in a circle is \( 360^\circ \).

1. Since the arcs BCD and BAD together make the complete circle, we have:
\( m(\text{arc BAD}) = 360^\circ - m(\text{arc BCD}) = 360^\circ - 140^\circ = 220^\circ \)

Step 4: Find the Measure of Angle ADB
To find angle ADB, we can use the properties of isosceles triangles and the fact that angles in a triangle sum up to \( 180^\circ \).

1. In triangle ABD, since \( AB = AD \), angles ADB and ABD are equal. Let \( \angle ADB = y \).
2. We know that:
\( \angle A + \angle B + \angle D = 180^\circ \)
where \( \angle A = 110^\circ \) (since \( \angle BAD = 110^\circ \)), and \( \angle B = \angle D = y \).
3. Thus, we can write:
\( 110^\circ + y + y = 180^\circ \)
\( 110^\circ + 2y = 180^\circ \)
\( 2y = 180^\circ - 110^\circ = 70^\circ \)
\( y = \frac{70^\circ}{2} = 35^\circ \)
Therefore, \( \angle ADB = 35^\circ \).

Final Answers
- \( m(\text{arc BCD}) = 140^\circ \)
- \( m(\text{arc BAD}) = 220^\circ \)
- \( \angle ADB = 35^\circ \)