The base BC of triangle ABC is divided at D so that BD = 12 DC.
Prove that area of ΔABD=13 of the area of ΔABC.
To prove that the area of triangle ΔABD is 13 of the area of triangle ΔABC, let's follow these steps:
Step 1: Understand the triangle and the point D
We have triangle ABC with base BC. Point D divides BC such that BD=12DC. This means that if we let DC=x, then BD=12x and thus BC=BD+DC=12x+x=32x.
Hint: Identify the relationships between the segments created by point D on base BC.
Step 2: Express the lengths in terms of a single variable
Let DC=x. Then, BD=12x and BC=32x.
Hint: Use a variable to simplify calculations and make relationships clearer.
Step 3: Draw the median AM
Draw the median AM from vertex A to the midpoint M of segment DC. Since M is the midpoint, we have DM=12DC=12x and CM=12DC=12x.
Hint: The median divides the triangle into two smaller triangles of equal area.
Step 4: Establish equal areas
Since AM is a median, it divides triangle ADC into two triangles ΔADM and ΔACM of equal area. Therefore, we can say:
Area of ΔADM=Area of ΔACM
Let’s denote the area of triangle ABC as S. Then, the area of triangle ADC is 23S because ΔABD and ΔADC together make up triangle ABC.
Hint: Use the property of medians to relate the areas of the triangles.
Step 5: Relate areas of triangles
Since BD=DM, triangle ABD is similar to triangle ADM. Therefore, the area of triangle ABD is equal to the area of triangle ADM:
Area of ΔABD=Area of ΔADM
Step 6: Calculate the area of triangle ABD
From the previous steps, we know:
Area of ΔABD=Area of ΔADM=12Area of ΔADC
Since the area of triangle ADC is 23S, we have:
Area of ΔABD=12⋅23S=13S
Conclusion
Thus, we have shown that the area of triangle ΔABD is 13 of the area of triangle ΔABC:
Area of ΔABD=13Area of ΔABC
Hint: Summarize the relationships and calculations to reinforce the conclusion.
We have triangle ABC with base BC. Point D divides BC such that BD=12DC. This means that if we let DC=x, then BD=12x and thus BC=BD+DC=12x+x=32x.
Let DC=x. Then, BD=12x and BC=32x.
Draw the median AM from vertex A to the midpoint M of segment DC. Since M is the midpoint, we have DM=12DC=12x and CM=12DC=12x.
Since AM is a median, it divides triangle ADC into two triangles ΔADM and ΔACM of equal area. Therefore, we can say:
Area of ΔADM=Area of ΔACM
Since BD=DM, triangle ABD is similar to triangle ADM. Therefore, the area of triangle ABD is equal to the area of triangle ADM:
Area of ΔABD=Area of ΔADM
From the previous steps, we know:
Area of ΔABD=Area of ΔADM=12Area of ΔADC
Area of ΔABD=12⋅23S=13S
Thus, we have shown that the area of triangle ΔABD is 13 of the area of triangle ΔABC:
Area of ΔABD=13Area of ΔABC
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)
36 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
In triangle ABC, D is a point in side BC such that 2BD=3DC. Prove that the area of triangle ABD = 35×Area ofΔABC
View SolutionAny point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
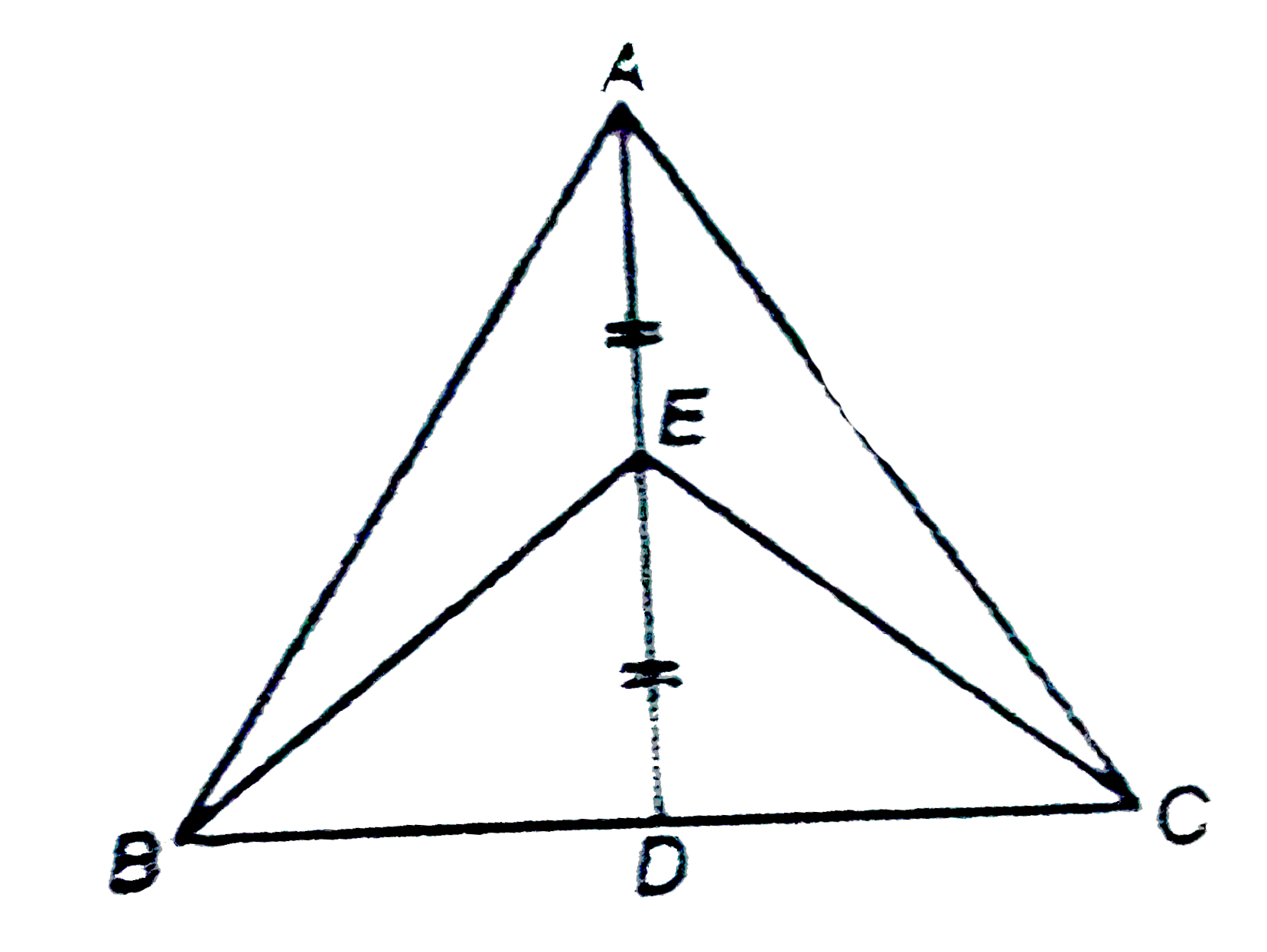
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View SolutionThe side BC of triangles ABC is produced to D so that CD = AC . If the angle BAD =109∘and the ACB =72∘ prove that BD is greater than AD.
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
View SolutionIn the following figure G, is centroid of the triangles ABC.
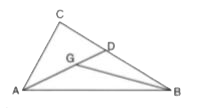
Prove that
Area (Δ AGB )=13× Area (ΔABC)
View Solution
