The cross-section of a canal is a trapezium in shape. If the canal is 10m wide at the top 6m wide at the bottom and the area of cross-section is determine its depth.
To determine the depth of the canal, we will use the formula for the area of a trapezium. The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where:
- a is the length of the top base,
- b is the length of the bottom base,
- h is the height (or depth in this case).
1. Identify the dimensions given in the problem:
- Top width a=10m
- Bottom width b=6m
- Area A=72m2
- Depth h=d (unknown)
2. Substitute the known values into the area formula:
72=12×(10+6)×d
3. Calculate the sum of the parallel sides:
10+6=16
So, the equation becomes:
72=12×16×d
4. Simplify the equation:
72=8d
5. Solve for d:
d=728=9
6. Conclusion:
The depth of the canal is 9m.
- a is the length of the top base,
- b is the length of the bottom base,
- h is the height (or depth in this case).
- Top width a=10m
- Bottom width b=6m
- Area A=72m2
- Depth h=d (unknown)
72=12×(10+6)×d
10+6=16
So, the equation becomes:
72=12×16×d
72=8d
d=728=9
The depth of the canal is 9m.
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBook:RD SHARMA ENGLISHChapter:LINEAR EQUATION IN ONE VARIABLEExercise:All Questions
Explore 110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)Book:RD SHARMA ENGLISHChapter:MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)Exercise:All Questions
Explore 134 Videos
Similar Questions
When the length and area of cross-section both are doubled, then its resistance
View SolutionThe following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.

If the width DC, of the swimming pool is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of cross-section.
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View SolutionThe adjoining figure shows a solid of uniform cross-section whch is a trapezium in shape. If the length of the solid is 1m, find its volume
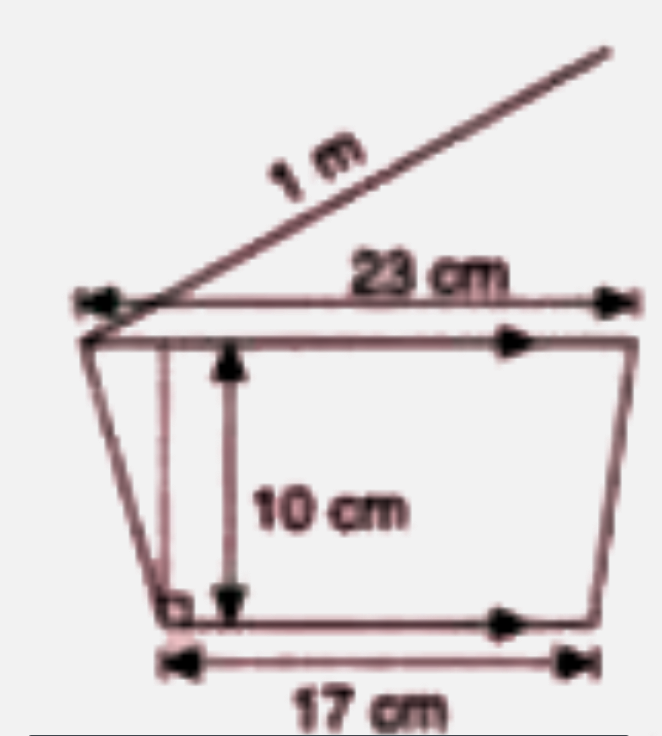
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View SolutionWater from a tap emerges vertically downwards with an initial spped of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15 m below the tap is
View SolutionResistance of the conductor of length 5m and area of cross -section 4mm2 s 0.02Ω. Its resistivity is
View SolutionA Steel wire is 1mlong and 1mm2 in area of cross-section. If it takes 200N to streach this wire by 1mm, the forces that will be required to stretch the wrie of the same material and cross-sectional area form a length of 10m to 1002cm
View SolutionWater from a tap emerges vertically downward with an initial speed of 3.0 m/s. The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is constant throughout the stream of water and that the flow is steady. The cross-sectional area of the stream 2 m below the tap is:
View Solution