The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long Calculate : the surface area of the tunnel (excluding the floor) .
The correct Answer is:2,000m2
To calculate the surface area of the tunnel (excluding the floor), we will follow these steps:
Step 1: Understand the shape of the tunnel
The cross-section of the tunnel consists of a square of side 7 meters, surmounted by a semicircle. The tunnel has a length of 80 meters.
Step 2: Calculate the area of the semicircle
1. Find the radius of the semicircle:
- The diameter of the semicircle is equal to the side of the square, which is 7 meters.
- Therefore, the radius r is:
r=72=3.5 meters
2. Calculate the area of the semicircle:
- The area A of a semicircle is given by the formula:
A=12πr2
- Substituting the radius:
A=12×227×(3.5)2
- Calculate (3.5)2=12.25:
A=12×227×12.25=22×12.2514=269.514≈19.9643 m2
Step 3: Calculate the area of the two side walls
1. Calculate the area of one side wall:
- The area of one wall is given by the formula:
Area of one wall=height×length=7×80=560 m2
2. Calculate the area of both side walls:
- Since there are two walls:
Total area of both walls=2×560=1120 m2
Step 4: Calculate the total surface area of the tunnel (excluding the floor)
1. Add the area of the semicircle and the area of the two walls:
- The total surface area S is given by:
S=Area of semicircle+Area of both walls
- Substituting the values:
S=19.9643+1120=1139.9643 m2
Step 5: Round off the answer
- The total surface area of the tunnel (excluding the floor) is approximately:
S≈1140 m2
Final Answer
The surface area of the tunnel (excluding the floor) is approximately 1140 m².
---
The cross-section of the tunnel consists of a square of side 7 meters, surmounted by a semicircle. The tunnel has a length of 80 meters.
1. Find the radius of the semicircle:
- The diameter of the semicircle is equal to the side of the square, which is 7 meters.
- Therefore, the radius r is:
r=72=3.5 meters
- The area A of a semicircle is given by the formula:
A=12πr2
- Substituting the radius:
A=12×227×(3.5)2
- Calculate (3.5)2=12.25:
A=12×227×12.25=22×12.2514=269.514≈19.9643 m2
1. Calculate the area of one side wall:
- The area of one wall is given by the formula:
Area of one wall=height×length=7×80=560 m2
2. Calculate the area of both side walls:
- Since there are two walls:
Total area of both walls=2×560=1120 m2
1. Add the area of the semicircle and the area of the two walls:
- The total surface area S is given by:
S=Area of semicircle+Area of both walls
- Substituting the values:
S=19.9643+1120=1139.9643 m2
- The total surface area of the tunnel (excluding the floor) is approximately:
S≈1140 m2
The surface area of the tunnel (excluding the floor) is approximately 1140 m².
Topper's Solved these Questions
Similar Questions
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long ,Calculate : its volume
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. Calculate: its floor area. The tunnel is 80 m long.
View SolutionThe cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle . The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 2.25 per m2
View SolutionFind the area of a square of side 8 m.
View SolutionThe cross-section of a railway tunnel is a square surmounted by a semi-circle as shown in the figure.
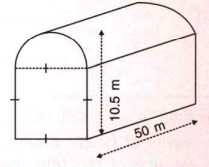
The tunnel is 50 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 10 per m2.
View SolutionFind the area of a square of side 14m.
View SolutionFind the area of a square plot of side 8 m.
View SolutionThe cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure, also given that: AM= BN, AB= 7m, CD= 5m. The height of the tunnel is 2.4m. The tunnel is 40m long. Calculate :
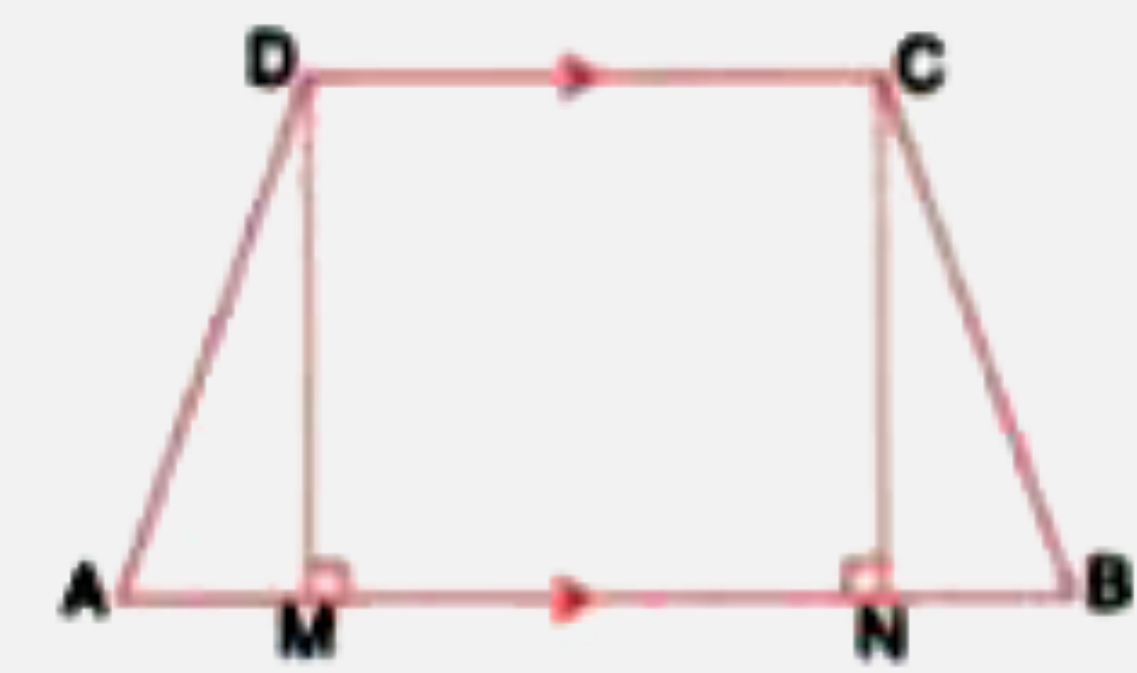
the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs 5 per m2 (sq. metre).
View SolutionA room is 4.5 m long 3.8 m broad . Calculate the area of the floor of the room.
View SolutionA cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
View Solution
