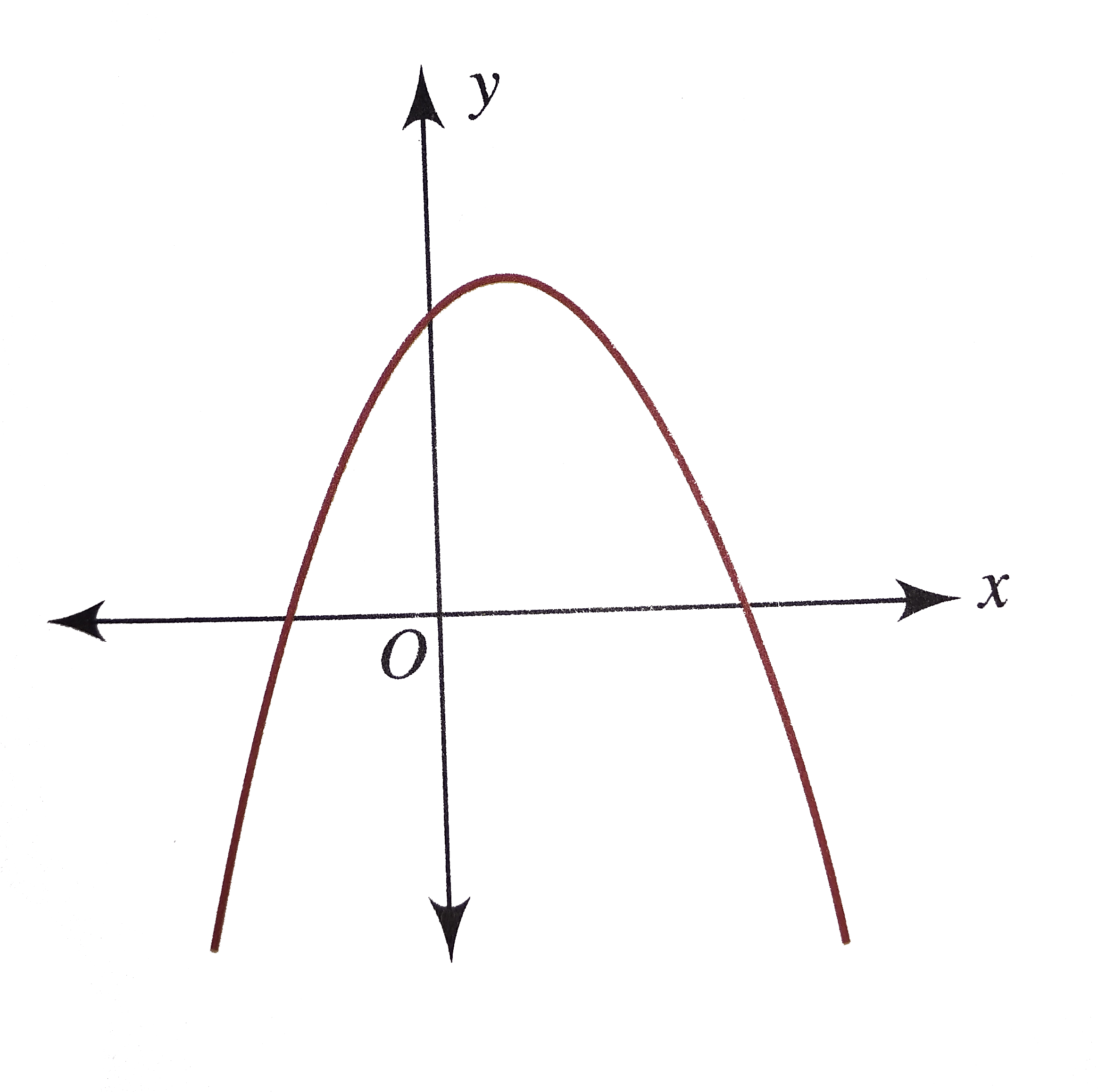
The following figure shows the graph of $f (x) = a x^{2} + b x + c$ , then find the sign of values of $a, b and c$ .

Video Solution

Text Solution

Verified by Experts

From the graph, $f (0) = c < 0$ (as the graph intersects the y-axis on the negative side)
Also the graph is concave upward $\Rightarrow a > 0$
Further the vertex lies on the left-hand side of the y-axis.
So the abscissa or the vertex $- \frac{b}{2 a} < 0$
$\Rightarrow b > 0$ (as $a > 0$ )

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $f (x) = a x^{2} + b x + c$ find $f^{1} (1)$ .
A $a + 2 b$
B $2 a - b$
C $a - 2 b$
D $2 a + b$

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile