The following table gives the number of finished articles turned out per day be different number of workers in a factors. Find the standard deviation of the daily output of finished articles. Find the variance and standard deviation of the following frequency distribution: Number of article:, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 No. of workers:, 3, 7, 11, 14, 18, 17, 13, 8, 5, 4
To find the variance and standard deviation of the given frequency distribution, we will follow these steps:
Step 1: Prepare the Data Table
We have the following data:
| Number of Articles (Xᵢ) | Number of Workers (fᵢ) |
|-------------------------|------------------------|
| 18 | 3 |
| 19 | 7 |
| 20 | 11 |
| 21 | 14 |
| 22 | 18 |
| 23 | 17 |
| 24 | 13 |
| 25 | 8 |
| 26 | 5 |
| 27 | 4 |
Step 2: Calculate the Assumed Mean (A)
Let's assume the mean (A) to be 22.
Step 3: Calculate Deviations (Dᵢ) and Squared Deviations (Dᵢ²)
Now, we will calculate the deviations (Dᵢ = Xᵢ - A) and their squares (Dᵢ²):
| Xᵢ | fᵢ | Dᵢ (Xᵢ - A) | Dᵢ² |
|----|----|-------------|-----|
| 18 | 3 | -4 | 16 |
| 19 | 7 | -3 | 9 |
| 20 | 11 | -2 | 4 |
| 21 | 14 | -1 | 1 |
| 22 | 18 | 0 | 0 |
| 23 | 17 | 1 | 1 |
| 24 | 13 | 2 | 4 |
| 25 | 8 | 3 | 9 |
| 26 | 5 | 4 | 16 |
| 27 | 4 | 5 | 25 |
Step 4: Calculate fᵢDᵢ and fᵢDᵢ²
Next, we will calculate the products of fᵢ and Dᵢ, and fᵢ and Dᵢ²:
| Xᵢ | fᵢ | Dᵢ | Dᵢ² | fᵢDᵢ | fᵢDᵢ² |
|----|----|----|-----|-------|--------|
| 18 | 3 | -4 | 16 | -12 | 48 |
| 19 | 7 | -3 | 9 | -21 | 63 |
| 20 | 11 | -2 | 4 | -22 | 44 |
| 21 | 14 | -1 | 1 | -14 | 14 |
| 22 | 18 | 0 | 0 | 0 | 0 |
| 23 | 17 | 1 | 1 | 17 | 17 |
| 24 | 13 | 2 | 4 | 26 | 52 |
| 25 | 8 | 3 | 9 | 24 | 72 |
| 26 | 5 | 4 | 16 | 20 | 80 |
| 27 | 4 | 5 | 25 | 20 | 100 |
Step 5: Calculate the Sums
Now, we will calculate the sums of fᵢ, fᵢDᵢ, and fᵢDᵢ²:
- Σfᵢ = 3 + 7 + 11 + 14 + 18 + 17 + 13 + 8 + 5 + 4 = 100
- ΣfᵢDᵢ = -12 - 21 - 22 - 14 + 0 + 17 + 26 + 24 + 20 + 20 = 38
- ΣfᵢDᵢ² = 48 + 63 + 44 + 14 + 0 + 17 + 52 + 72 + 80 + 100 = 490
Step 6: Calculate Variance (σ²)
Using the formula for variance:
\sigma^2 = \frac{\Sigma fᵢDᵢ²}{\Sigma fᵢ} - \left(\frac{\Sigma fᵢDᵢ}{\Sigma fᵢ}\right)^2
Substituting the values:
σ2=490100−(38100)2
Calculating:
σ2=4.9−(0.38)2
σ2=4.9−0.1444=4.7556≈4.76
Step 7: Calculate Standard Deviation (σ)
The standard deviation is the square root of the variance:
σ=√4.76≈2.18
Final Answers
- Variance (σ²) ≈ 4.76
- Standard Deviation (σ) ≈ 2.18
---
We have the following data:
|-------------------------|------------------------|
| 18 | 3 |
| 19 | 7 |
| 20 | 11 |
| 21 | 14 |
| 22 | 18 |
| 23 | 17 |
| 24 | 13 |
| 25 | 8 |
| 26 | 5 |
| 27 | 4 |
Let's assume the mean (A) to be 22.
Now, we will calculate the deviations (Dᵢ = Xᵢ - A) and their squares (Dᵢ²):
|----|----|-------------|-----|
| 18 | 3 | -4 | 16 |
| 19 | 7 | -3 | 9 |
| 20 | 11 | -2 | 4 |
| 21 | 14 | -1 | 1 |
| 22 | 18 | 0 | 0 |
| 23 | 17 | 1 | 1 |
| 24 | 13 | 2 | 4 |
| 25 | 8 | 3 | 9 |
| 26 | 5 | 4 | 16 |
| 27 | 4 | 5 | 25 |
Next, we will calculate the products of fᵢ and Dᵢ, and fᵢ and Dᵢ²:
|----|----|----|-----|-------|--------|
| 18 | 3 | -4 | 16 | -12 | 48 |
| 19 | 7 | -3 | 9 | -21 | 63 |
| 20 | 11 | -2 | 4 | -22 | 44 |
| 21 | 14 | -1 | 1 | -14 | 14 |
| 22 | 18 | 0 | 0 | 0 | 0 |
| 23 | 17 | 1 | 1 | 17 | 17 |
| 24 | 13 | 2 | 4 | 26 | 52 |
| 25 | 8 | 3 | 9 | 24 | 72 |
| 26 | 5 | 4 | 16 | 20 | 80 |
| 27 | 4 | 5 | 25 | 20 | 100 |
Now, we will calculate the sums of fᵢ, fᵢDᵢ, and fᵢDᵢ²:
- ΣfᵢDᵢ = -12 - 21 - 22 - 14 + 0 + 17 + 26 + 24 + 20 + 20 = 38
- ΣfᵢDᵢ² = 48 + 63 + 44 + 14 + 0 + 17 + 52 + 72 + 80 + 100 = 490
Using the formula for variance:
\sigma^2 = \frac{\Sigma fᵢDᵢ²}{\Sigma fᵢ} - \left(\frac{\Sigma fᵢDᵢ}{\Sigma fᵢ}\right)^2
σ2=4.9−0.1444=4.7556≈4.76
The standard deviation is the square root of the variance:
- Variance (σ²) ≈ 4.76
- Standard Deviation (σ) ≈ 2.18
Topper's Solved these Questions
Similar Questions
Find the variance and standard deviation of the following data:
 View Solution
View SolutionFind the mean and standard deviation of the following frequency distribution :
 View Solution
View SolutionFind the variance and standard deviation from the following data:
 View Solution
View SolutionFind the variance and standard deviation of the following distribution
 View Solution
View SolutionEstimate standard deviation for the following frequency distribution.
 View Solution
View SolutionFind the variance and standard deviation for the following distribution.
 View Solution
View SolutionCalculate variance and standard deviation for the following distribution.
 View Solution
View SolutionFind the standard deviation of the following distribution :
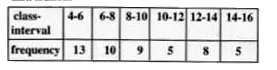 View Solution
View SolutionFind the variance and standard deviation of the following data 5,12,3,18,6,8,2,10
View SolutionFind out the standard deviation from the following distribution table:
 View Solution
View Solution

