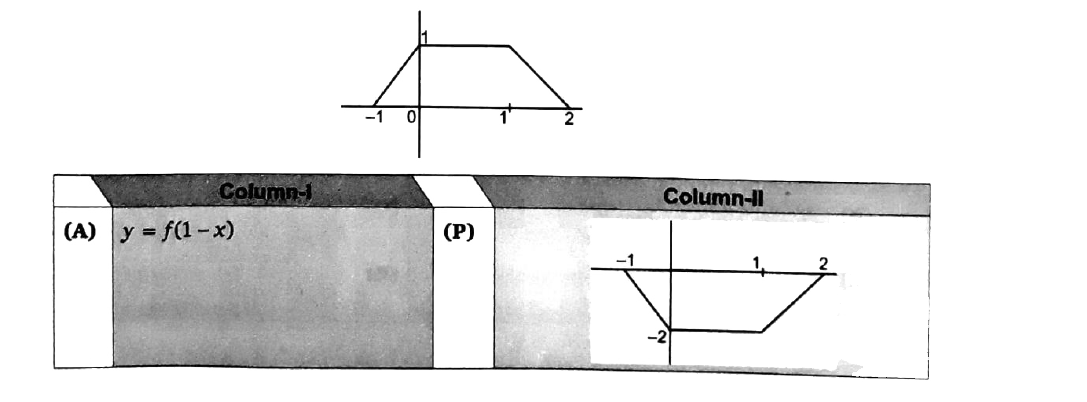
The graph of y=f(x) is given above. For what value of x is y=f(x-4) undefined?
The correct Answer is:D
Difficult:Easy
Category: Passport to Advanced Math/ Functions
Strategic Advice: Algebraically, a function is undefined when value (or values ) in its domain cannot be evaluted (for example, taking the square root of a negative number or dividing by 0). Graphically, this produces a "hole" (or an asymptote) in the graph.
Getting to the Answer: The graph of f(x), which is show, is undefined at x=1 because there is a hole in the graph, meaning that the function asks where the transformed (shifted) function is undefined. The notation represents a horizontal shifts of f(x) to the right 4 units (remember, horizontal shifts are always the opposite of how they appear), so imagine moving the hole shown in the graph to the right 4units. The result is (5,2), so the shifted function is undefined at x=5, which is (D).
Topper's Solved these Questions
Similar Questions
Knowledge Check
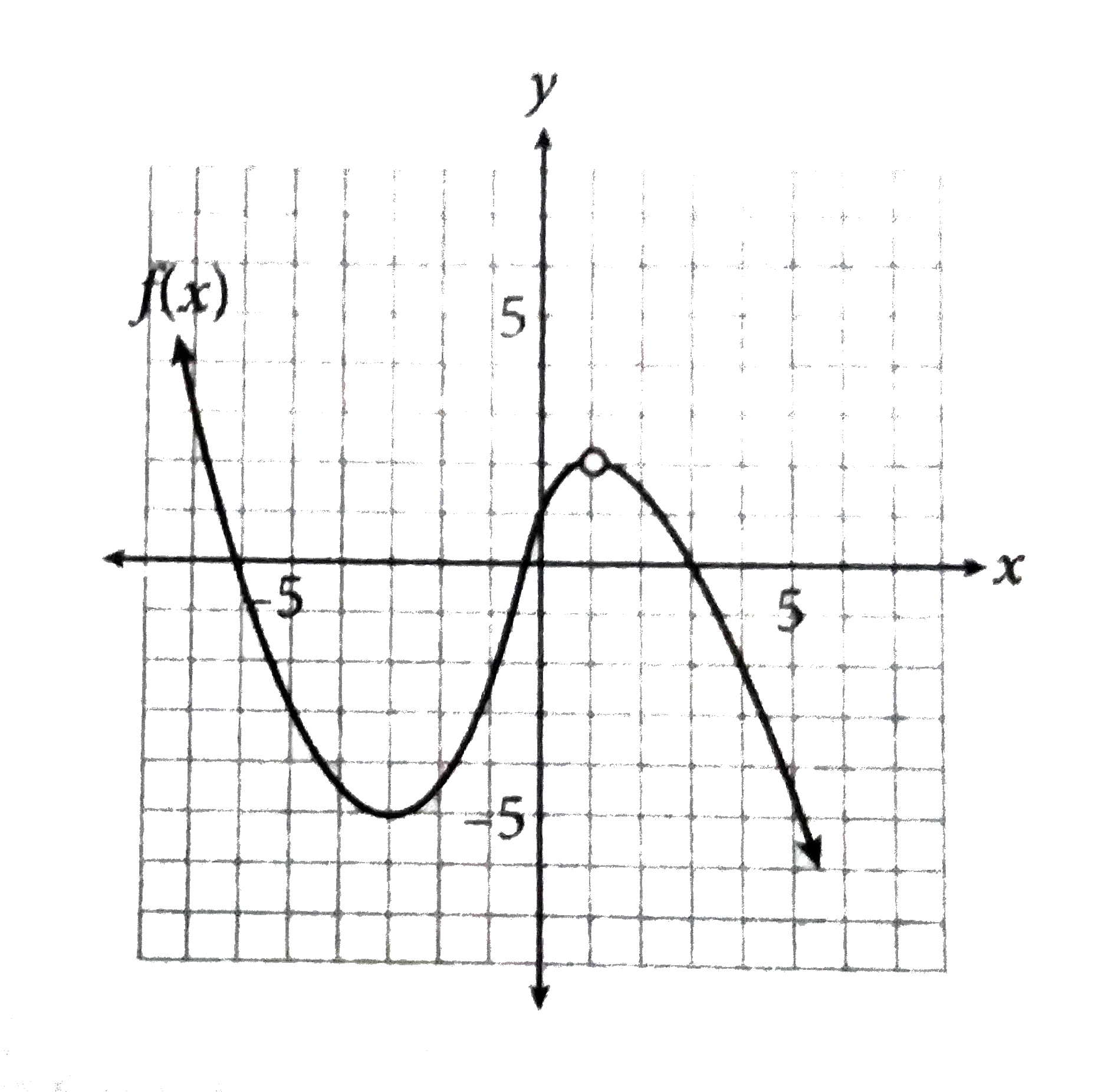
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?A−5B−3C−2D3
The graph of y=f(x) is given below
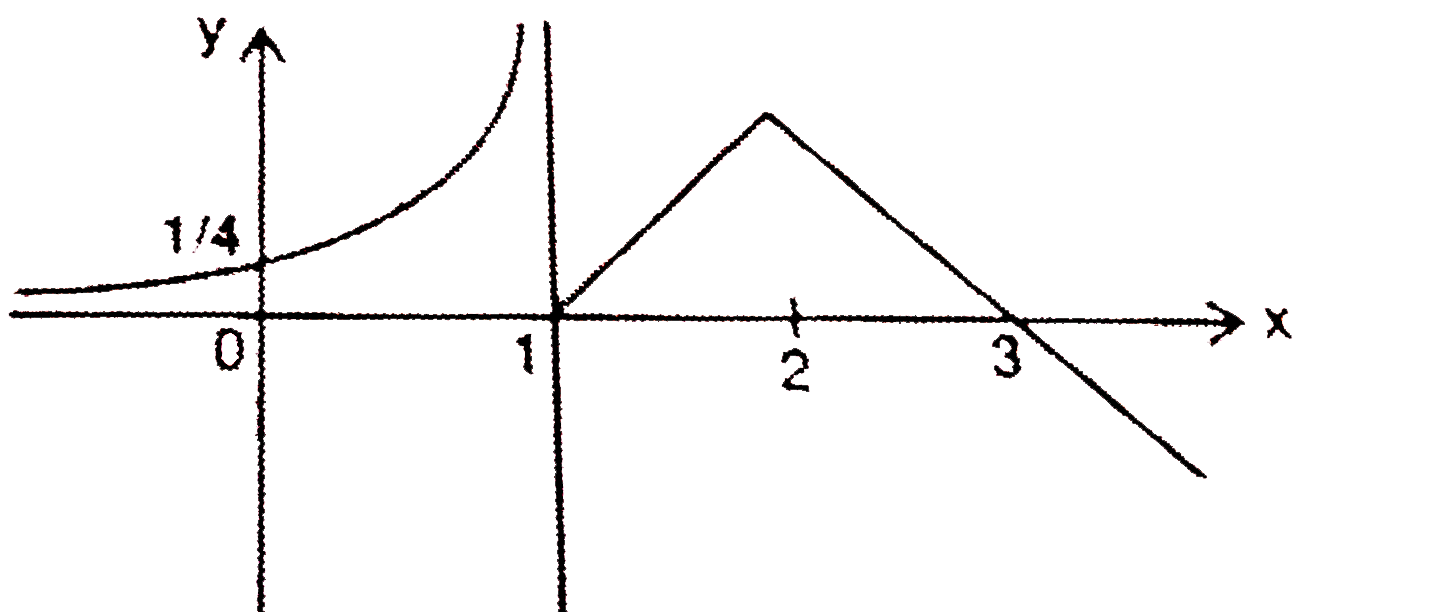
then the graph y=|f(|x|)| is :
View Solution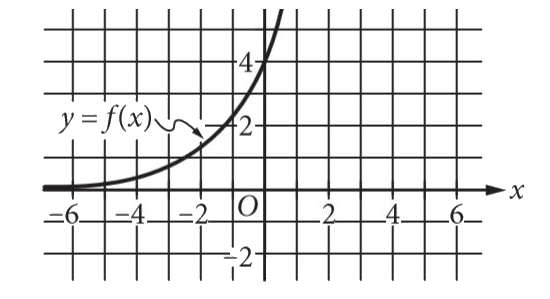
The graph of y = f (x) is shown in the xy -plane. What is the value of f (0) ?
View Solution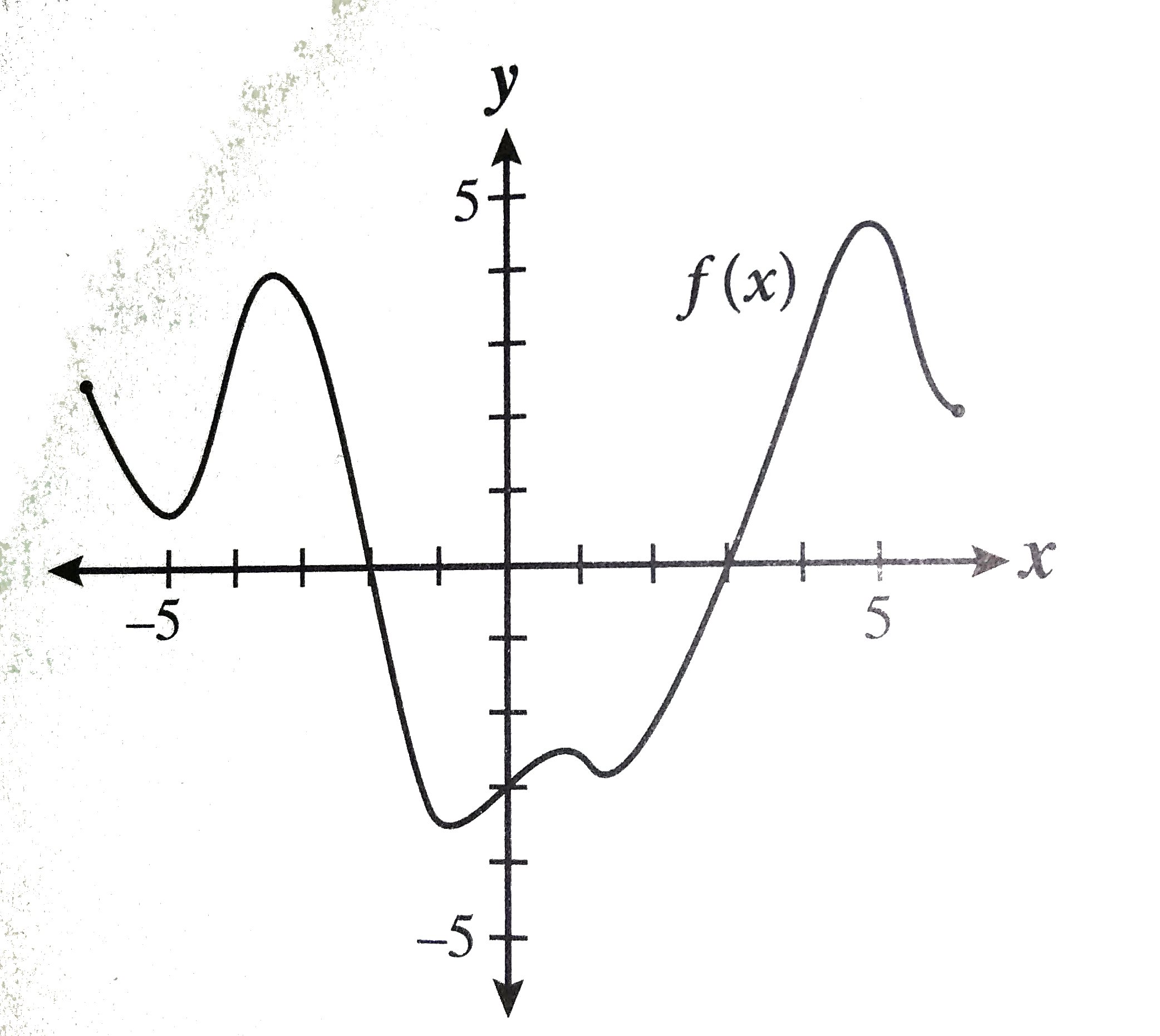
The figure above shows the graph of f(x). For which value(s) of x does f(x) equal 0?
View SolutionThe graph y = f (x) is as shown:
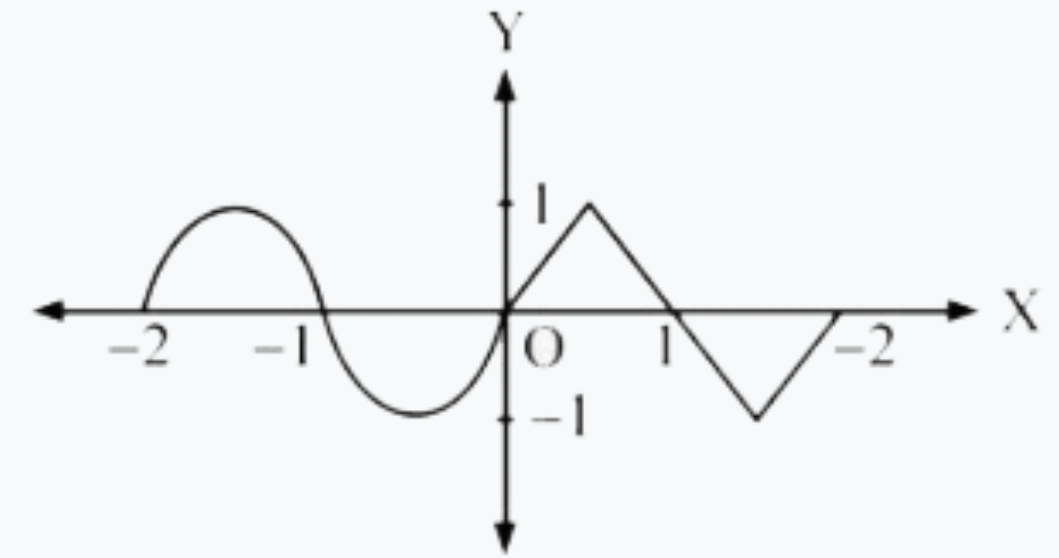
The graph of y = f (–|x|) is:
View SolutionConsider that the graph of y=f(x) is symmetrie about the lines x=2andx=4 then the period of f(x) is
View SolutionIf the graph of y=|f(x)| is as shown in figure
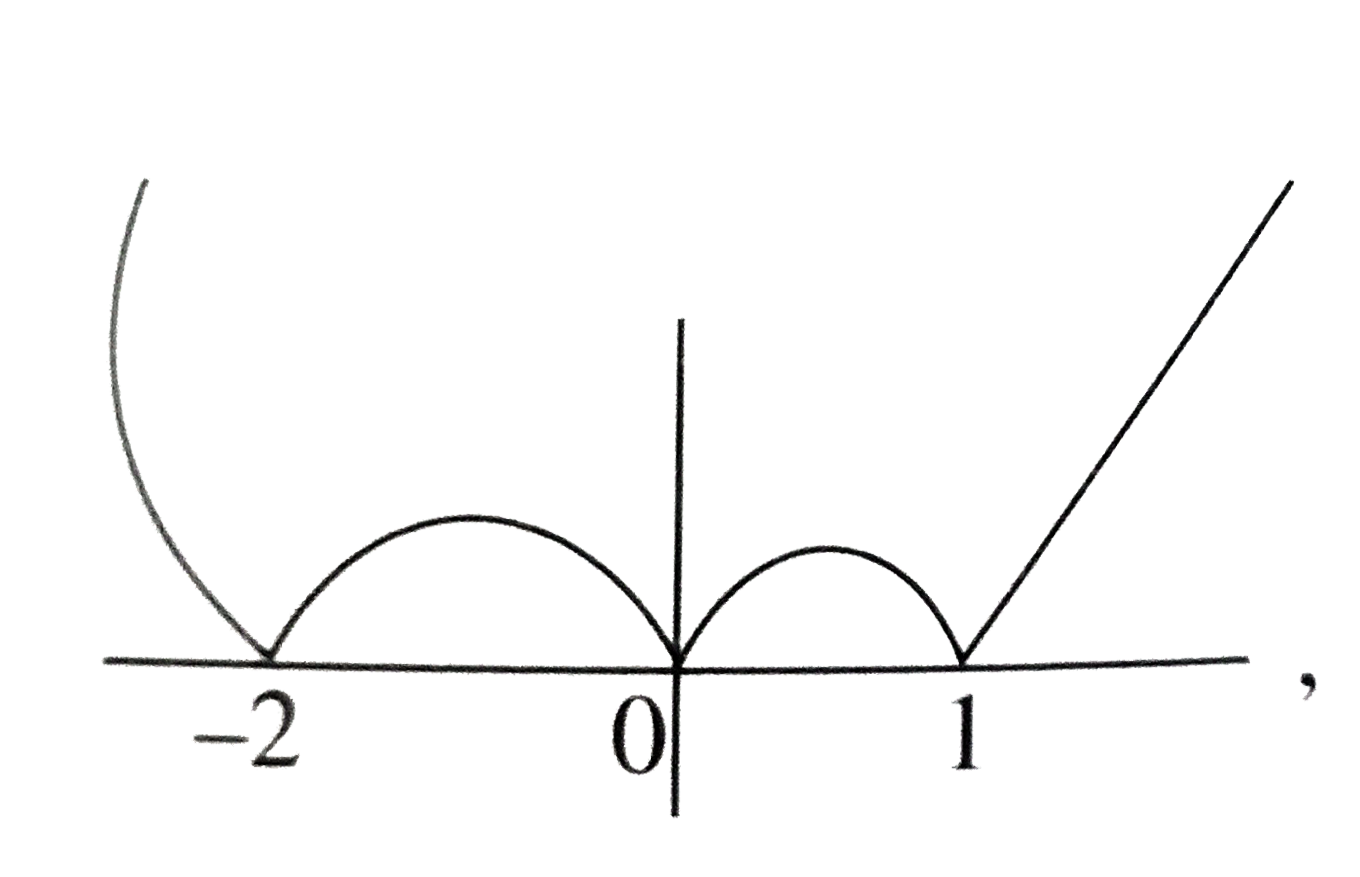 then the graph of y=f(x) may be
then the graph of y=f(x) may be
View SolutionFollowing is the graph of y = f'(x) and f(0) = 0 .
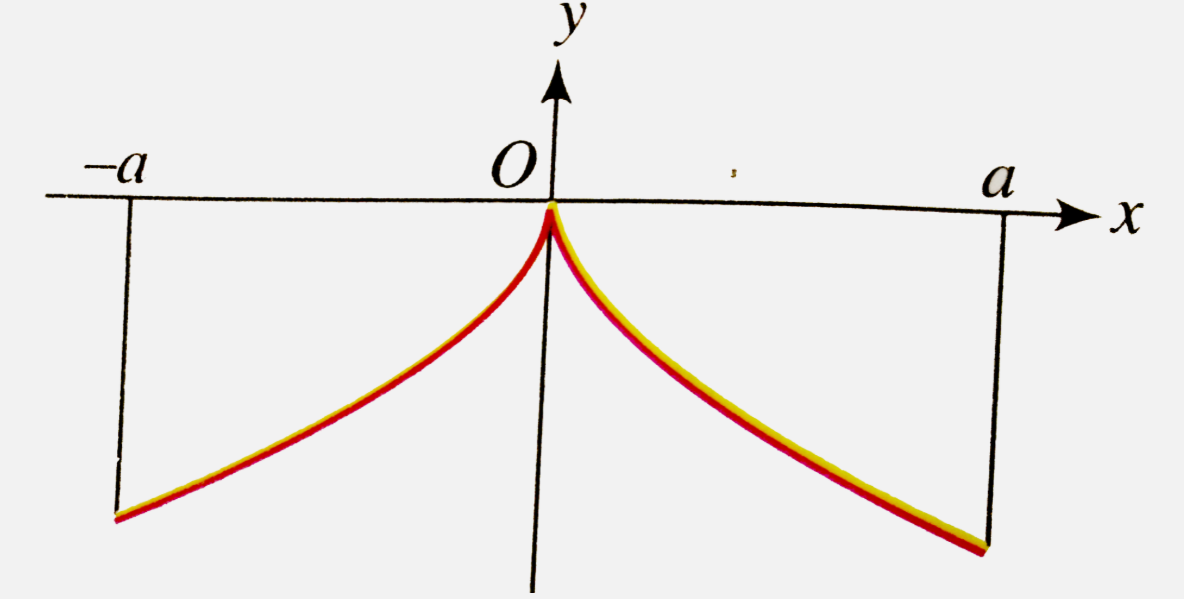
(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?
View Solution