The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. What is the radius of the circle.
The correct Answer is:7 cm
To find the radius of the circle given the length of the tangent and the distance from the point to the center, we can follow these steps:
1. Identify the Given Information:
- Length of the tangent (AP) = 24 cm
- Distance from point P to the center O (OP) = 25 cm
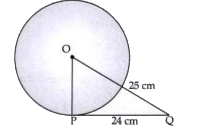
2. Draw the Diagram:
- Draw a circle with center O.
- Mark point P outside the circle such that OP = 25 cm.
- Draw the tangent line from point P to the circle, touching the circle at point A. The length of the tangent PA = 24 cm.
3. Apply the Right Triangle Concept:
- The radius OA is perpendicular to the tangent PA at point A. Therefore, triangle OAP is a right triangle with:
- OP as the hypotenuse,
- OA as one leg (the radius we need to find),
- AP as the other leg (the length of the tangent).
4. Use the Pythagorean Theorem:
- According to the Pythagorean theorem:
OP2=OA2+AP2
- Substitute the known values:
252=OA2+242
5. Calculate the Squares:
- Calculate 252 and 242:
625=OA2+576
6. Rearrange the Equation:
- To find OA2:
OA2=625−576
OA2=49
7. Find the Radius:
- Take the square root of both sides to find OA (the radius):
OA=√49=7 cm
Final Answer:
The radius of the circle is 7 cm.
---
- Length of the tangent (AP) = 24 cm
- Distance from point P to the center O (OP) = 25 cm
- Draw a circle with center O.
- Mark point P outside the circle such that OP = 25 cm.
- Draw the tangent line from point P to the circle, touching the circle at point A. The length of the tangent PA = 24 cm.
- The radius OA is perpendicular to the tangent PA at point A. Therefore, triangle OAP is a right triangle with:
- OP as the hypotenuse,
- OA as one leg (the radius we need to find),
- AP as the other leg (the length of the tangent).
- According to the Pythagorean theorem:
OP2=OA2+AP2
- Substitute the known values:
252=OA2+242
- Calculate 252 and 242:
625=OA2+576
- To find OA2:
OA2=625−576
OA2=49
- Take the square root of both sides to find OA (the radius):
OA=√49=7 cm
The radius of the circle is 7 cm.
Topper's Solved these Questions
- CIRCLESBook:CBSE COMPLEMENTARY MATERIALChapter:CIRCLESExercise:SHORT ANSWER TYPE - I QUESTIONS
Explore 10 Videos
- CIRCLESBook:CBSE COMPLEMENTARY MATERIALChapter:CIRCLESExercise:SHORT ANSWER TYPE - II QUESTIONS
Explore 4 Videos
- ARITHMETIC PROGRESSION Book:CBSE COMPLEMENTARY MATERIALChapter:ARITHMETIC PROGRESSION Exercise:PRACTICE TEST (SECTION D)
Explore 1 Video
- Co-ordinate GeometryBook:CBSE COMPLEMENTARY MATERIALChapter:Co-ordinate GeometryExercise:PRACTICE-TEST (Coordinate Geometry) SECTION-D
Explore 1 Video
Similar Questions
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
View SolutionFrom a point Q, the length of the tangent to a circle is 12 cm and distance of d from the centre is 13 cm. Find the radius of the circle.
View Solution
Knowledge Check
From a point A, the length of the tangent to ta circle is 24 cm . And the distance of a from the centre is 25 cm . The radius of the circle is
A7 cmB12 cmC15 cmD24.5 cmFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm, the radius of the circle is
A7 cmB12 cmC15 cmD24.5 cmThe length of tangent drawn to a circle with radius 7 cm from a point 25 cm away the centre , is
A24 cmB27 cmC26 cmD25 cm
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
View SolutionThe length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
View SolutionThe length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle ?
View SolutionFind the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
View SolutionFrom an external point Q, the length of the tangents to a circle is 5 cm and the distance of Q from the centre is 8 cm. The radius of the circle is:
View Solution