The number of such points (a+1,√3a), where a is any integer, lying inside the region bounded by the circles x2+y2−2x−3=0 and x2+y2−2x−15=0, is
Video Solution
Text Solution
We have circles (x−1)2+y2=4 (1)
and (x−1)2+y2=16 (2)
Circles are concentric having centre at C(1,0) and radii 2 and 4.
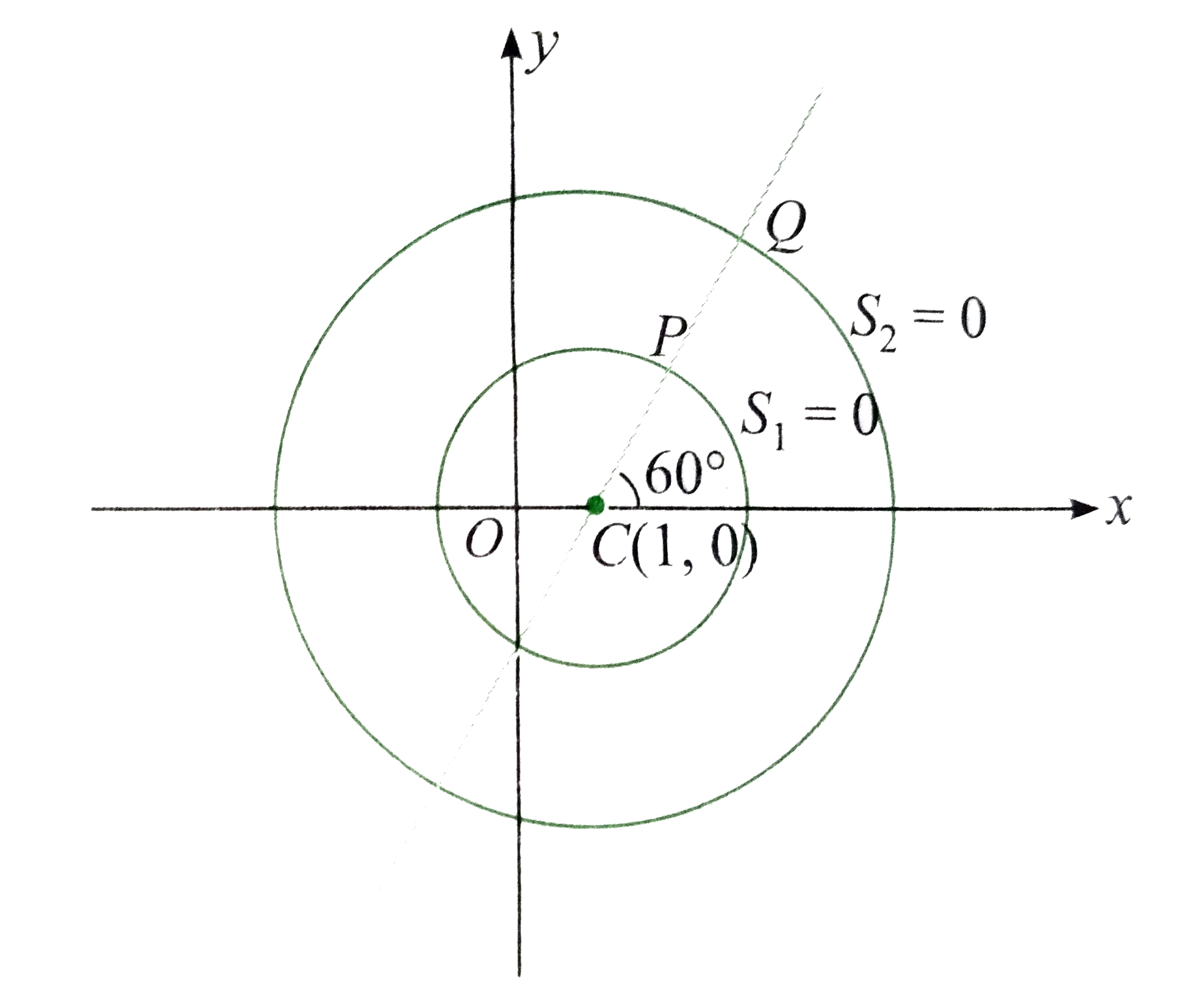
Variable point (a+1,√3a) lies on the line y=√3(x−1) , which passes through centre of the circles having inclination 60∘.
Line meets circles at P(1+2cos60∘,2sin60∘)and Q(1+4cos60∘,4sin60∘).
Thus, P≡(2,√3) and Q≡(3,2√3)
∴a∈(2,3)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The point ([P + 1], [P]) (where, [x] is the greatest integer function) lying inside the region bounded by the circle x2+y2−2x−15=0 and x2+y2−2x−7=0 , then
AP∈[−1,2)−{0,1}BP∈[−1,0)∪(0,1)∪(1,2]CP∈(−1,2)Dnone of theseThe area of region bounded by circles x2+y2=1 and (x−1)2+y2=1 is :
A2π3 sq. unitsB√32 sq. unitsC(2π3−√32) sq. unitsDNone of theseThe area of the region bounded by x2+y2−2x−3=0andy=|x|+1 is
Aπ2−1 sq. unitsB2π sq. unitsC4π sq. unitsDπ/2 sq. units
Find the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0 and x=3.
View SolutionFind the area of the region bounded by the curves y=x2+2y=x,x=0,andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2;y=x;x=0 and x=3
View SolutionThe point (P+1P) (where [.] denotes the greatest integer function), lyinginside the region bounded by the circle x2+y2−2x−15=0andx2+y2−2x−7=0, then :
View Solution