The P lies on side AB of an equilateral triangle ABC. Arrange AC, AP and CP in descending order.
To solve the problem of arranging the lengths AC, AP, and CP in descending order, we can follow these steps:
1. Understanding the Triangle:
- We have an equilateral triangle ABC, which means all sides are equal: AC=AB=BC.
2. Position of Point P:
- Point P lies on side AB. Therefore, the length AP is less than the length AB (since P is a point on AB).
- This implies that AP<AB.
3. Comparing AP and AC:
- Since AB=AC (because ABC is an equilateral triangle), we can conclude that:
AP<AB=AC
- Thus, we have:
AP<AC
4. Using Angles to Compare CP and AP:
- In triangle ABC, angle A, angle B, and angle C are all equal (each being 60∘).
- The line segment CP divides angle C into two parts, say α and β, where α+β=∠C.
- Since α<∠C, we can conclude that:
α<60∘
5. Applying the Angle-Side Relationship:
- According to the property of triangles, the side opposite the smaller angle is shorter. Therefore, since AP is opposite angle A and CP is opposite angle C:
AP<CP
- This means:
AP<CP
6. Final Comparison:
- Now we have two inequalities:
1. AP<AC
2. AP<CP
- To arrange them in descending order, we can compare:
- Since AC=AB and AP<AC and AP<CP, we can conclude that:
AC>CP>AP
Conclusion:
Thus, the final arrangement in descending order is:
AC>CP>AP
- We have an equilateral triangle ABC, which means all sides are equal: AC=AB=BC.
- Point P lies on side AB. Therefore, the length AP is less than the length AB (since P is a point on AB).
- This implies that AP<AB.
- Since AB=AC (because ABC is an equilateral triangle), we can conclude that:
AP<AB=AC
- Thus, we have:
AP<AC
- In triangle ABC, angle A, angle B, and angle C are all equal (each being 60∘).
- The line segment CP divides angle C into two parts, say α and β, where α+β=∠C.
- Since α<∠C, we can conclude that:
α<60∘
- According to the property of triangles, the side opposite the smaller angle is shorter. Therefore, since AP is opposite angle A and CP is opposite angle C:
AP<CP
- This means:
AP<CP
- Now we have two inequalities:
1. AP<AC
2. AP<CP
- To arrange them in descending order, we can compare:
- Since AC=AB and AP<AC and AP<CP, we can conclude that:
AC>CP>AP
Thus, the final arrangement in descending order is:
AC>CP>AP
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - MID- POINT THEOREM
9 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - PYTHAGORAS THEOREM
5 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.
View SolutionLet a point P lies inside an equilateral △ABC such that its perpendicular distances from sides are P1,P2,P3.If side length of △ABC is 2 unit then
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
∠CAD=∠BAE
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD=∠BAE
(ii) CD = BE
View SolutionLet the point P lies in the interior of an equilateral triangle with side lengths 2 units, each. Find the sum of the shortest distances from P to the sides of the triangle.
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
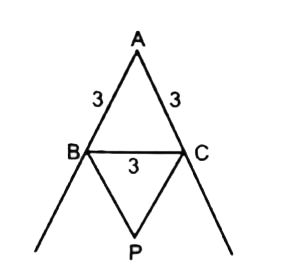
View SolutionSides AB and AC in an equilateral triangle ABC with side length 3 is extended to form two rays from point A as shown in the figure. Point P is chosen outside the triangle ABC and between the two rays such that ∠ABP+∠BCP=180∘. If the maximum length of CP is M, then M2/2 is equal to :
View SolutionThe side of a triangle are in A.P. Its area is 35 the of an equilateral triangle of the same perimeter. Show that the sides are in the proportion 3:5:7.
View SolutionConstruct an equilateral ΔABC such that AB=4.2cm.
View SolutionThe sides of a triangle are in A.P. and its area is 35th of the an equilateral triangle of the same perimeter, prove that its sides are in the ratio 3:5:7, and find the greatest angle of the triangle.
View Solution
