The probability distribution function of a random variable X is given by xi:012 pi:3c34c−10c25c−1 Where c>0 Find : (i) c (ii) P(X<2) (ii) P(1<X≤2)
To solve the problem step by step, we will follow the instructions given in the video transcript.
Step 1: Find the value of c
We are given the probability distribution function of a random variable X as follows:
xi:0,1,2
pi:3c3,4c−10c2,5c−1
Since the sum of all probabilities must equal 1, we can write the equation:
3c3+(4c−10c2)+(5c−1)=1
Combining the terms, we have:
3c3−10c2+9c−2=0
Step 2: Solve the polynomial equation
To find the roots of the polynomial 3c3−10c2+9c−2=0, we can use synthetic division or polynomial long division. We will check if c=1 is a root:
Substituting c=1:
3(1)3−10(1)2+9(1)−2=3−10+9−2=0
Since c=1 is a root, we can factor the polynomial as:
3c3−10c2+9c−2=(c−1)(3c2−7c+2)
Step 3: Factor the quadratic
Now we need to solve the quadratic equation 3c2−7c+2=0. We can use the quadratic formula:
c=−b±√b2−4ac2a
Here, a=3,b=−7,c=2:
c=7±√(−7)2−4⋅3⋅22⋅3
=7±√49−246
=7±√256
=7±56
This gives us:
c=126=2andc=26=13
Step 4: Determine valid values for c
We have three potential values for c: 1,2,13. However, we need to ensure that the probabilities are valid (i.e., they must be between 0 and 1).
- For c=2:
- p(0)=3(23)=24 (not valid)
- For c=1:
- p(0)=3(13)=3 (not valid)
- For c=13:
- p(0)=3(13)3=19
- p(1)=4(13)−10(13)2=43−109=129−109=29
- p(2)=5(13)−1=53−1=23
All probabilities sum to 1:
19+29+69=1
Thus, the valid value for c is:
c=13
Step 5: Calculate P(X<2)
To find P(X<2), we need to calculate P(X=0)+P(X=1):
P(X<2)=P(X=0)+P(X=1)=19+29=39=13
Step 6: Calculate P(1<X≤2)
To find P(1<X≤2), we need to calculate P(X=2):
P(X=2)=23
Final Answers
(i) The value of c is 13.
(ii) P(X<2)=13.
(iii) P(1<X≤2)=23.
pi:3c3,4c−10c2,5c−1
=7±√49−246
=7±√256
=7±56
- p(0)=3(23)=24 (not valid)
- For c=1:
- p(0)=3(13)=3 (not valid)
- p(0)=3(13)3=19
- p(1)=4(13)−10(13)2=43−109=129−109=29
- p(2)=5(13)−1=53−1=23
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, isA1.76B2.45C3.2D4.8
If the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View SolutionThe following is a probability distribution function of a random variable :

(i) Find k (ii) Find P(X>3) (iii) Find P(−3<X<4)
(iv) Find P(X<−3).View SolutionConsider the probability distribution of a random variable X

Calculate
(i) V(X2) (ii) Variance of X.View SolutionThe probability distribution of a random variable X is given below
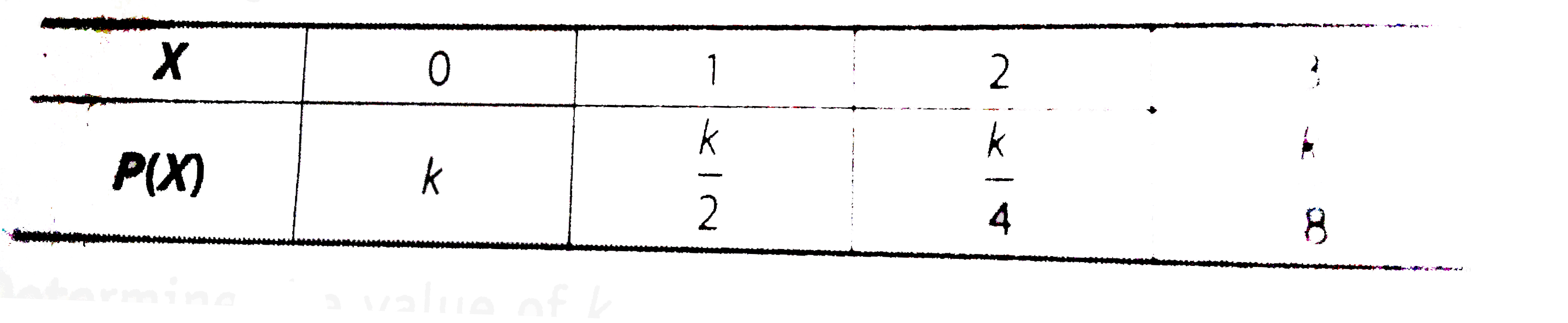
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).View SolutionA probability distribution of a variable X is given below: X:01234 P(X):0.10.250.30.20.15 Find (i) Var(X) (ii) Var(X2)
View Solution
The probability distribution of a random variable 'X', taking values 1, 2, 3, 4, 5 is given :
(a) Find the value of p.
(b) Find the mean of X.
( c ) Find the variance of X.View SolutionThe probability distribution for a random variable X is as follows:
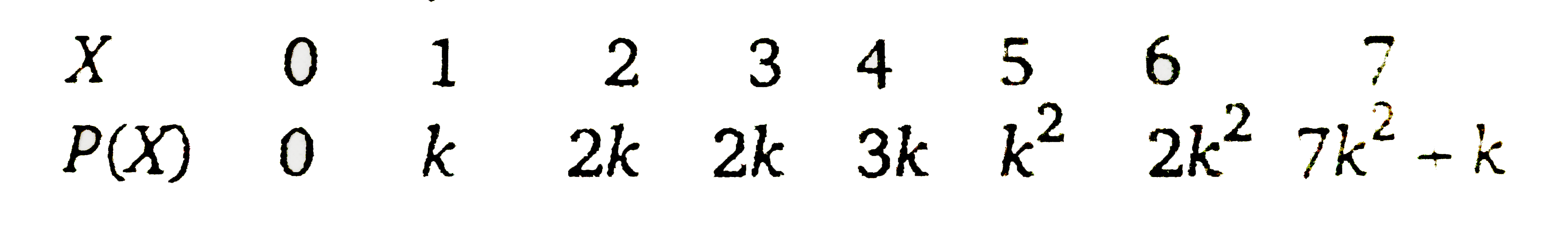
Find:
(i) k (ii) P(X≥3)
(iii) P(X≥6) (iv) P(0<X<3)View Solution


