The probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
To solve the problem, we need to follow these steps:
Step 1: Define the Probability Distribution
We are given the probability distribution of a random variable X:
P(X=x)=⎧⎨⎩kx2for x=1,2,32kxfor x=4,5,60otherwise
Step 2: Create a Probability Table
We will create a table to list the values of P(X=x):
| x | P(X=x) |
|---------|--------------|
| 1 | k⋅12=k |
| 2 | k⋅22=4k |
| 3 | k⋅32=9k |
| 4 | 2k⋅4=8k |
| 5 | 2k⋅5=10k |
| 6 | 2k⋅6=12k |
Step 3: Sum of Probabilities
The sum of all probabilities must equal 1:
k+4k+9k+8k+10k+12k=1
Calculating the left side:
44k=1⟹k=144
Step 4: Calculate P(X≥4)
Now we can find P(X≥4):
P(X≥4)=P(X=4)+P(X=5)+P(X=6)
Substituting the values:
P(X=4)=8k,P(X=5)=10k,P(X=6)=12k
Calculating:
P(X≥4)=8k+10k+12k=30k=30⋅144=3044=1522
Step 5: Calculate E(X)
The expected value E(X) is calculated as follows:
E(X)=6∑i=1xiP(X=xi)
Calculating each term:
E(X)=1⋅k+2⋅4k+3⋅9k+4⋅8k+5⋅10k+6⋅12k
Calculating:
E(X)=k+8k+27k+32k+50k+72k=190k=190⋅144=19044=9522
Step 6: Calculate E(3X2)
Now we calculate E(3X2):
E(3X2)=36∑i=1x2iP(X=xi)
Calculating each term:
E(3X2)=3(12⋅k+22⋅4k+32⋅9k+42⋅8k+52⋅10k+62⋅12k)
Calculating:
E(3X2)=3(k+16k+81k+128k+250k+432k)=3⋅908k=2724k=2724⋅144=272444=68111
Final Answers
1. P(X≥4)=1522
2. E(X)=9522
3. E(3X2)=68111
---
We are given the probability distribution of a random variable X:
We will create a table to list the values of P(X=x):
|---------|--------------|
| 1 | k⋅12=k |
| 2 | k⋅22=4k |
| 3 | k⋅32=9k |
| 4 | 2k⋅4=8k |
| 5 | 2k⋅5=10k |
| 6 | 2k⋅6=12k |
The sum of all probabilities must equal 1:
Now we can find P(X≥4):
The expected value E(X) is calculated as follows:
Now we calculate E(3X2):
1. P(X≥4)=1522
2. E(X)=9522
3. E(3X2)=68111
Topper's Solved these Questions
Similar Questions
The probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View SolutionLet X be a discrete random variable whose probability distribution is defined as follows: P(X=x)={k(x+1)forx=1,2,3,42kxforx=5,6,70otherwise , where k is a constant. Find (i) k (ii) E(X) (iii) standard deviation of X.
View SolutionThe probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, is
View SolutionThe probability distribution for a random variable X is as follows:
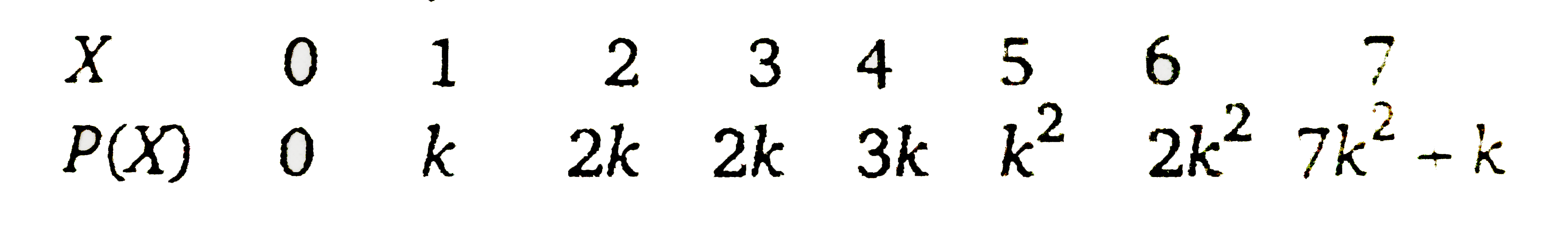
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View SolutionThe probability distribution of a discrete random variable x is given as under

Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionThe probability distribution of a random variable is given below:
X=x01234567P(X=x)0k2k2k3kk22k27k2+k
Then P(0<X<5)=
View SolutionIf the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View Solution
