The shaded region for the inequality x+5y≤6 is
A
to the non-origin side of x + 5y =6
B
to the either side of x+5y=6
C
to the origin side of x+5y=6
D
to the neither side of x+5y=6
Video Solution
Text Solution
The correct Answer is:C
Given inequality is
x+5y≤6
On putting x =0 and y=0 we get
0+5.0=0≤6 (true)
So given inequality represents region for given constraints is the line segement EG.
|
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
The shaded region for the inequality x+5y≤6 is
Aat the non-origin side of x+5y=6Bto the origin side of x+5y=6Cto the either side of x+5y=6Dto the either side of x−5y=6The graph of the inequality 4x+6y≤24 is :
Ahalf plane that contains the origin, including the points on the line 4x+6y=24.Bhalf plane that does not contain the origin.Centire XOY plane.Dhalf plane that contains the origin.The Corner points of feasible region for the inequations , x+y≤5,x+2y≤6,x≥0,y≥0 are
A(0,3),(5,0),(0,5),(6,0)B(0,3),(5,0),(4,1),(0,0)C(0,0),(1,4),(5,0),(0,3)D(3,0),(0,5)(0,0),(4,1)
The region represented by the inequality 2<|z+i|≤3 is . . . .
View SolutionWhich of the following shaded regions shows the graph of the inequality y≤|x+2| ?
View SolutionThe shaded region is represented by the inequality:
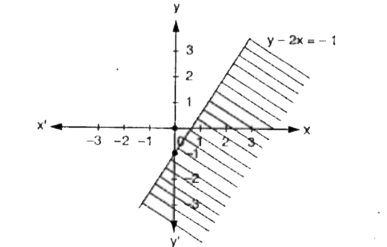
View SolutionThe graph of inequality 3x+y≤3 is:
View SolutionSolution set for inequality |x−1|≤5is.
View Solution
