Question

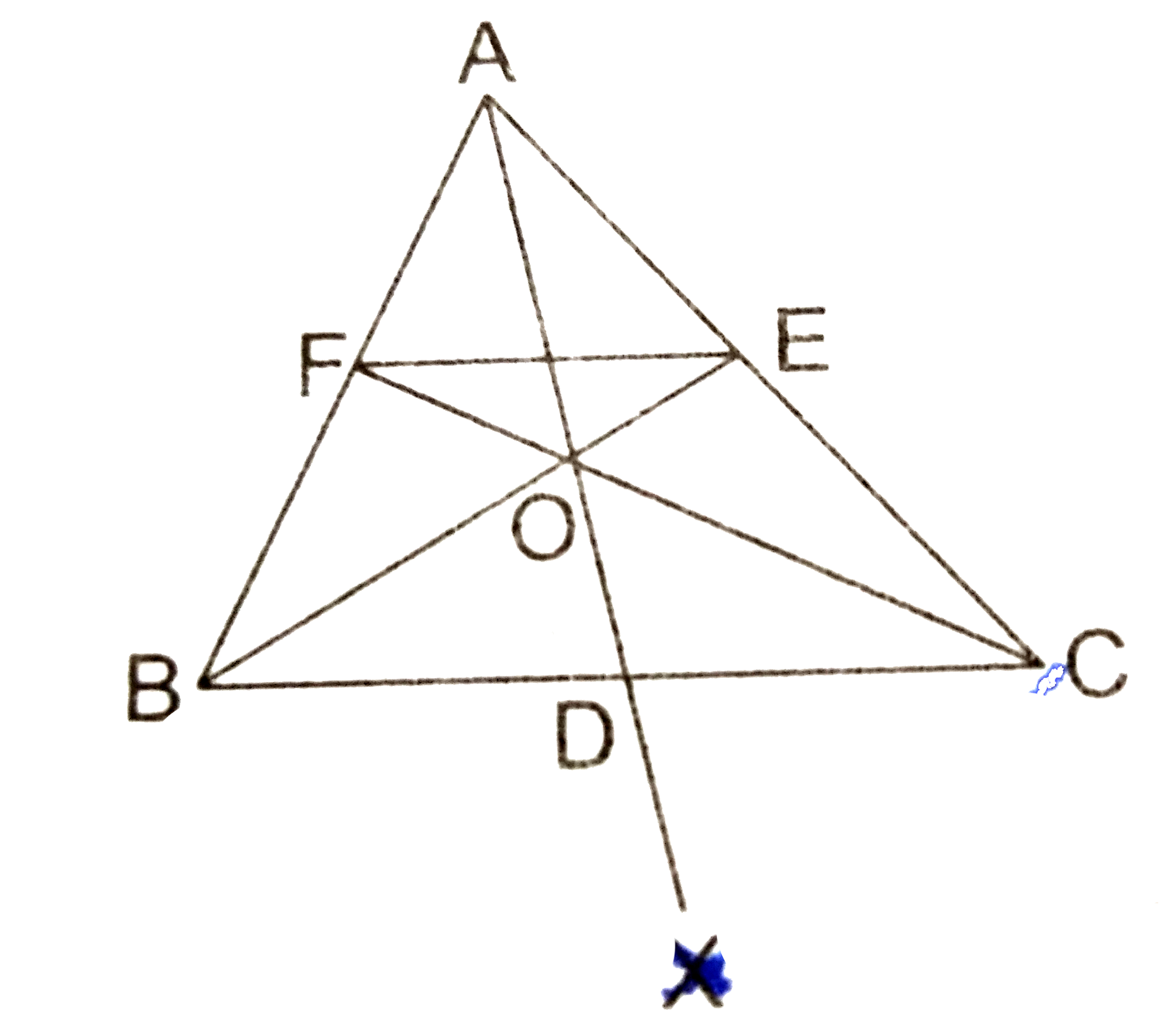
The side $BC$
of a triangle $ABC$
is bisected at $D;o$
is any point in $AD,BOandCO$
produced meet $ACandAB$
in $EandF$
respectively and $AD$
is produced to $X$
so that $D$
is the mid-point of $OX\stackrel{.}{}$
Prove that $AO:AX=AF:AB$
and show that $FEBC\stackrel{.}{}$

Explanation

Join BX and CX.
Since D is the mid -point of BC ( given )
BD= DC …(1)
Also D is the mid-point of OX (given )
OD= DX … (2)
From (1) and (2) we, have
`squareOBXC` is a parallelogram ( diagonals bisect each other)
OC||BX ( opposite sides of a parallelogram)
`Rightarrow FC||BX Rightarrow FO ||BX`
`In DeltaABX, (AO)/(OX)= (AF)/(FB)` ( by B.P theorem) ...(3)
Also , BO||XC ( opposite sides of a parallelogram)
` Rightarrow BE||XCRightarrow OE||XC`
` (AO)/(OX)= (AE)/(EC)` (by B.P theorem) ...(4)
From (3) and (4) , we have
`1 ( AF)/(FB) = (AE) (EC)`
In ` DeltaABC, FE||BC.` (converse of B.P theorem) Hence Proved.