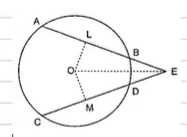
Two chords AB and CD of a circle are perpendicular to each other. If perpendicular drawn to AD from the point of intesection of those two chords AB and CD is produced to meet BC at the point E prove that the point E is the mid- point of BC.Solution in Bengali
Now,
Again, opposite angles] .........(3)
Now, ltbgt
from (3) and (4) we get
Similary it can be proved that
Then from (5) and (6) we get BE=CE
Hence E is the mid-point of BC.

Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionIn the figure,two equal chords AB and CD of a circle with centre O ,intersect each other at E , Prove that AD=CB
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure, Prove that BE=DE and AE=CE.
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View Solutionवृत्त का व्यास PQ दो जीवाओं AB तथा CD को क्रमशः M तथा N बिन्दुओं पर समद्विभाजक करता है। सिद्ध करने की AB∣∣CD
View SolutionO The two chords AB and CD of a central circle intersect at the point P. Prove that angleAOD+angleBOC=2angleBPC . If angleAOD Oh angleBOC If they complement each other, then we prove that the two chords are perpendicular to each other.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View Solutionएक वृत्त जिसका केन्द्र O है, के दो लम्ब AB तथा CD एक-दूसरे के लम्बवत हैं । जीवा BC की लम्बाई है
View Solutionएक वृत्त जिसका केन्द्र O है, के दो लम्ब AB तथा CD एक-दूसरे के लम्बवत हैं । जीवा BC की लम्बाई है
View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ=150∘ find angleAPQ
View Solution
