Two circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
Given: Two circles with centres A and B intersect at C and D. To Prove : ∠ACB=∠ADB
Construction: Join AC, AD, BC, BD and AB.
Proof : In ΔACB and ΔADB,
AC=AD [Radii of the same circle]
BC=BD [Radii of the same circle]
AB=AB [Common]
∴ΔACB≅ΔADB [By SSS]
∴∠ACB=∠ADB [By CPCT]
Hence Proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D. then.
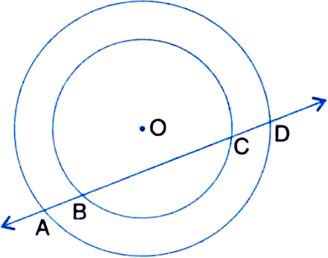 AAB=BDBCD=ACCAB=CDDNone
AAB=BDBCD=ACCAB=CDDNone
If a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
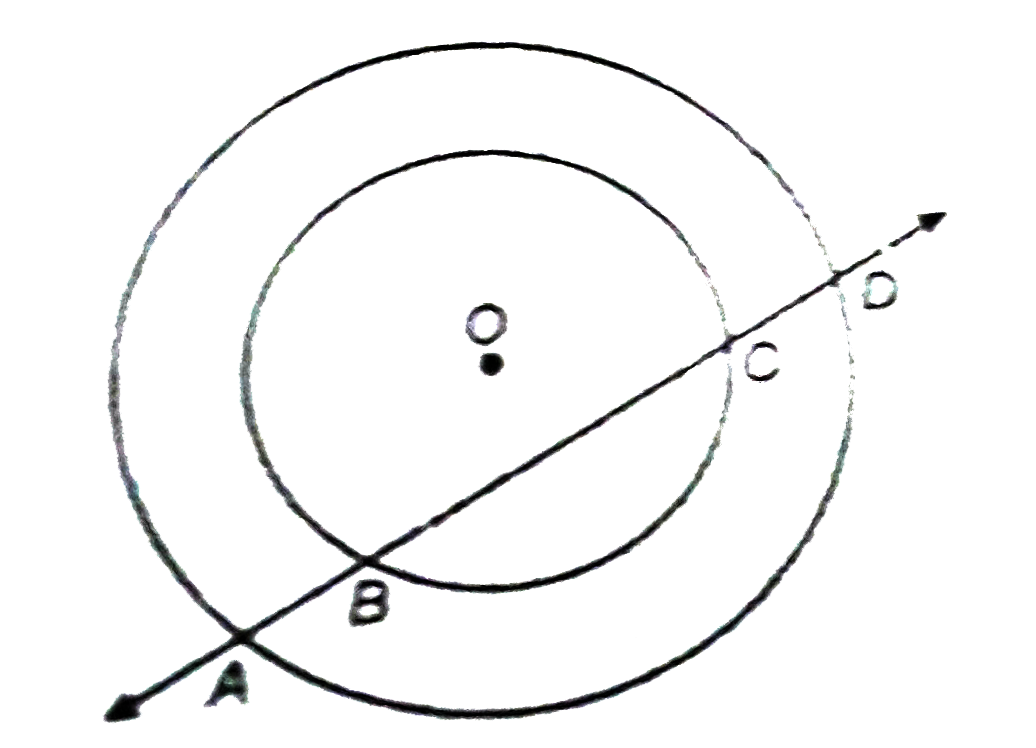 View Solution
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
View SolutionIn Figure, ∠E>∠A and ∠C>∠D . Prove that AD>EC
 View Solution
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionIf the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O such that ∠C+∠D=k∠AOB, then find the value of k
View Solution

