The angle in a semi-circle is a right angle.
To prove that the angle in a semicircle is a right angle, we can follow these steps:
1. Identify the Circle and Points:
Let’s consider a circle with center O. We will take points P and Q on the circumference of the circle such that the line segment PQ is a diameter of the circle. Let R be any point on the circumference of the circle.
2. Understand the Angles:
We need to prove that the angle PRQ (the angle subtended by the arc PQ at point R) is equal to 90 degrees.
3. Use the Angle at the Center:
According to the property of circles, the angle subtended by an arc at the center of the circle (angle POQ) is twice the angle subtended by the same arc at any point on the circumference (angle PRQ).
Mathematically, this can be expressed as:
∠POQ=2×∠PRQ
4. Determine the Angle at the Center:
Since P and Q are endpoints of the diameter, the angle POQ is a straight line. Therefore, we know:
∠POQ=180∘
5. Set Up the Equation:
Now, substituting the known value of angle POQ into the equation from step 3:
180∘=2×∠PRQ
6. Solve for Angle PRQ:
To find angle PRQ, divide both sides of the equation by 2:
∠PRQ=180∘2=90∘
7. Conclusion:
Therefore, we have proven that the angle PRQ, which is the angle in the semicircle, is indeed a right angle:
∠PRQ=90∘
Let’s consider a circle with center O. We will take points P and Q on the circumference of the circle such that the line segment PQ is a diameter of the circle. Let R be any point on the circumference of the circle.
We need to prove that the angle PRQ (the angle subtended by the arc PQ at point R) is equal to 90 degrees.
According to the property of circles, the angle subtended by an arc at the center of the circle (angle POQ) is twice the angle subtended by the same arc at any point on the circumference (angle PRQ).
∠POQ=2×∠PRQ
Since P and Q are endpoints of the diameter, the angle POQ is a straight line. Therefore, we know:
∠POQ=180∘
Now, substituting the known value of angle POQ into the equation from step 3:
180∘=2×∠PRQ
To find angle PRQ, divide both sides of the equation by 2:
∠PRQ=180∘2=90∘
Therefore, we have proven that the angle PRQ, which is the angle in the semicircle, is indeed a right angle:
∠PRQ=90∘
Topper's Solved these Questions
Similar Questions
Using vector method, prove that the angel in a semi circle is a right angle.
View SolutionTheorem:-5 (i) The degree measure of an arc or angle subtended by an arc at the centre is double the angle subtended by it at any point of alternate segment. (ii) Angle in the same segment of a circle are equal (iii) The angle in the semi circle is right angle.
View SolutionShow that any angle in a semi-circle is a right angle.
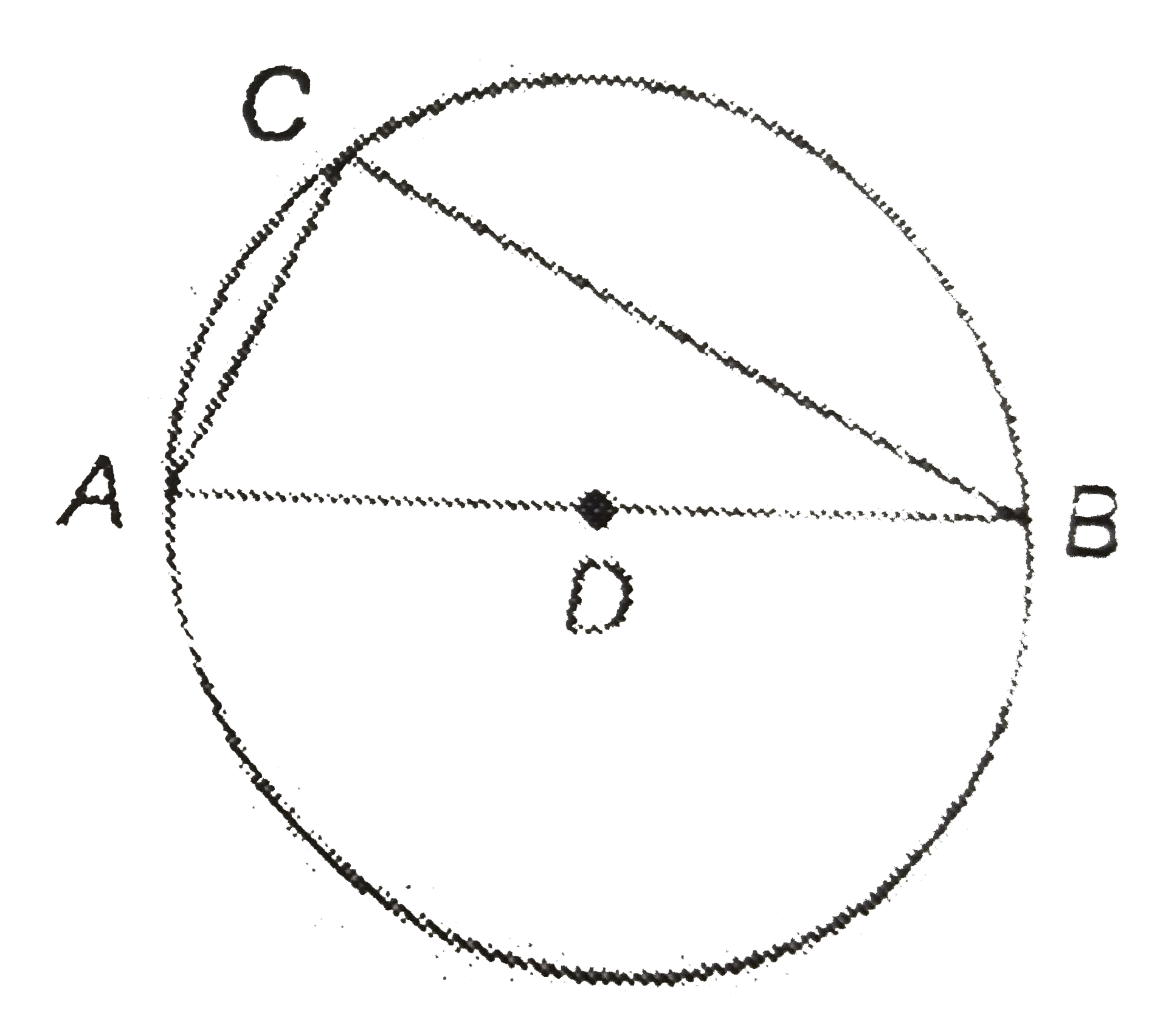
The following arc the steps involved in showing the above result. Arrange them in sequential order.
A) ∴∠ACB=180∘2=90∘
B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle.
c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC.
D) ∴∠AD=2×∠ACB
180∘=2∠ACB(∴∠ADB=180∘)
 View Solution
View SolutionProve that an angle inscribed in a semi-circle is a right angle using vector method.
View SolutionEach angle of a rectangle is a right angle.
View SolutionProve that the angle in a segment greater than a semi-circle is less than a right angle.
View SolutionShow that each angle of a rectangle is a right angle.
View SolutionProperty 1 each angle of a rectangle is a right angle.
View SolutionShow that each angle of a rectangle is a right angle
View SolutionEach of the four angles of a rectangle is a right angle.
View Solution

