Two circles touch externally at a point P. From a external point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ=TR.
To prove that TQ=TR where TQ and TR are tangents drawn from an external point T to two circles that touch externally at point P, we can follow these steps:
Step 1: Identify the Circles and Tangents
Let the two circles be C1 and C2 that touch each other externally at point P. From the external point T, draw tangents TQ to circle C1 and TR to circle C2 with points of contact at Q and R respectively.
Step 2: Use the Tangent Properties
According to the properties of tangents, the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can state:
- TQ is the tangent from point T to circle C1.
- TR is the tangent from point T to circle C2.
Step 3: Establish Equal Lengths
Since TQ and TR are tangents drawn from the same external point T:
- The length of the tangent from point T to circle C1 (which is TQ) is equal to the length of the tangent from point T to circle C2 (which is TR).
- Therefore, we can write:
TQ = TP_1 \quad \text{(where TP_1 isthetangenttocircle C_1 )}
TR = TP_2 \quad \text{(where TP_2 isthetangenttocircle C_2 )}
Step 4: Conclude the Proof
Since both tangents from point T to each circle are equal:
TQ=TR
Thus, we have proved that TQ=TR.
Let the two circles be C1 and C2 that touch each other externally at point P. From the external point T, draw tangents TQ to circle C1 and TR to circle C2 with points of contact at Q and R respectively.
According to the properties of tangents, the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can state:
- TQ is the tangent from point T to circle C1.
- TR is the tangent from point T to circle C2.
Since TQ and TR are tangents drawn from the same external point T:
- The length of the tangent from point T to circle C1 (which is TQ) is equal to the length of the tangent from point T to circle C2 (which is TR).
- Therefore, we can write:
TQ = TP_1 \quad \text{(where TP_1 isthetangenttocircle C_1 )}
TR = TP_2 \quad \text{(where TP_2 isthetangenttocircle C_2 )}
Since both tangents from point T to each circle are equal:
TQ=TR
Thus, we have proved that TQ=TR.
Topper's Solved these Questions
Similar Questions
Two tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
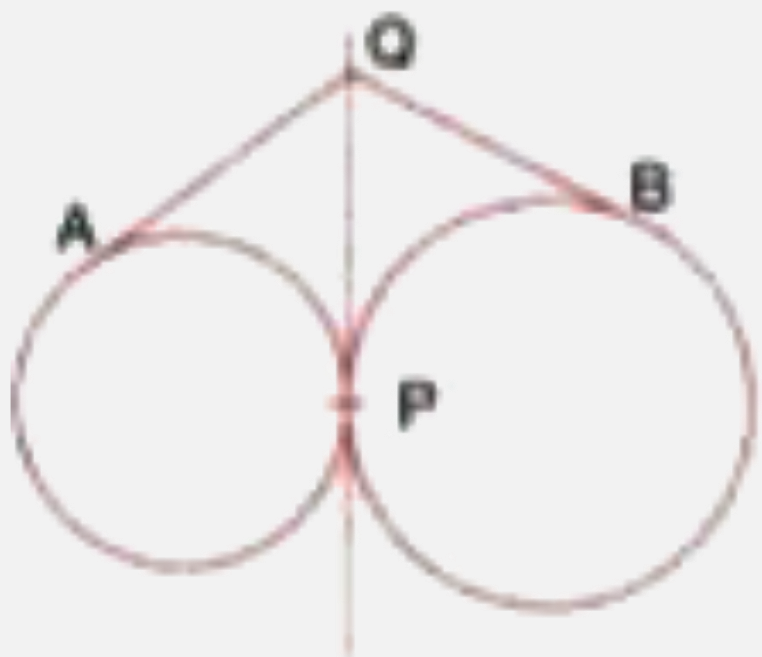 View Solution
View SolutionAB is the diameter of a circle with centre O. A line PQ touches the given circle at point R and cuts the tangents to the circle through A and B at points P and Q respectively. Prove that ∠POQ=90∘
View SolutionCircles of radii 3,4,5 touch each other externally . Let P be the point of intersection of tangents of these circles at their points of contact .Show that the distance of P from a point of contact is √5.
View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View Solution

