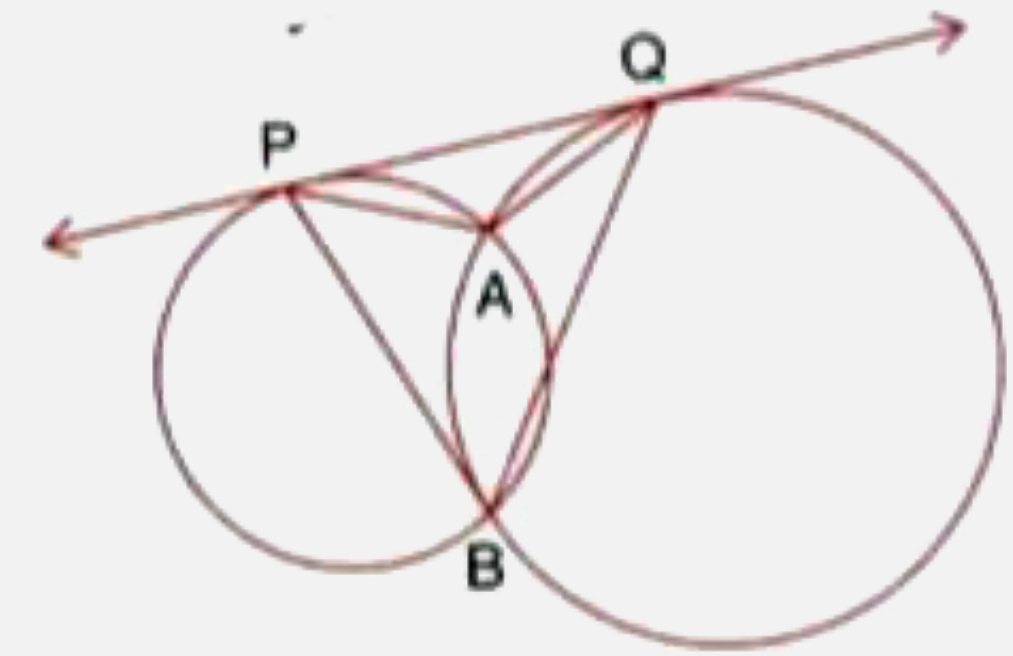
Two congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
To prove that BP=BQ when two congruent circles intersect at points A and B, and a line segment PAQ is drawn such that P and Q lie on the two circles, we can follow these steps:
1. Identify the Circles and Points:
Let the two congruent circles be C1 and C2, intersecting at points A and B. Draw the line segment PAQ such that P lies on circle C1 and Q lies on circle C2.
Hint: Visualize the two circles and mark the points of intersection clearly.
2. Common Chord:
The line segment AB is a common chord of both circles C1 and C2.
Hint: Remember that a common chord is a line segment that is part of both circles.
3. Angles at Point A:
Since P and Q are points on the circles, the angles ∠APB and ∠AQB are formed. By the property of circles, these angles are equal because they subtend the same arc AB in both circles.
Hint: Use the property that angles subtended by the same chord in equal circles are equal.
4. Triangles Involved:
Consider triangle BPQ. We have ∠APB=∠AQB.
Hint: Look at the triangles formed and note the relationships between the angles.
5. Applying the Isosceles Triangle Theorem:
Since ∠APB=∠AQB, and AB is the common chord, by the Isosceles Triangle Theorem, the sides opposite to these equal angles must also be equal. Therefore, BP=BQ.
Hint: Recall that in an isosceles triangle, the sides opposite to equal angles are equal.
6. Conclusion:
Thus, we have shown that BP=BQ.
Hint: Summarize your findings to conclude the proof clearly.
Final Statement:
Hence, we have proved that BP=BQ as required.
Let the two congruent circles be C1 and C2, intersecting at points A and B. Draw the line segment PAQ such that P lies on circle C1 and Q lies on circle C2.
The line segment AB is a common chord of both circles C1 and C2.
Since P and Q are points on the circles, the angles ∠APB and ∠AQB are formed. By the property of circles, these angles are equal because they subtend the same arc AB in both circles.
Consider triangle BPQ. We have ∠APB=∠AQB.
Since ∠APB=∠AQB, and AB is the common chord, by the Isosceles Triangle Theorem, the sides opposite to these equal angles must also be equal. Therefore, BP=BQ.
Thus, we have shown that BP=BQ.
Hence, we have proved that BP=BQ as required.
Similar Questions
In the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circels. Prove that PBQ is a straight line.

View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circels. Prove that PBQ is a straight line.

View SolutionTwo circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Figure). Prove that ∠ACP=∠QCD.
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View SolutionThe congruent circles with centres Oand O' intersect at two points A and B. Then, ∠AOB=∠AO'B.
View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View SolutionProve that two different circles cannot intersect each other at more than two points.
View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionTwo circles with centres O and O'are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. prove that OA bisects angle BAC.

View Solution