The congruent circles with centres Oand O' intersect at two points A and B. Then, .
The correct Answer is:1
To determine whether the statement "angle AOB = angle AO'B" is true for two congruent circles with centers O and O' that intersect at points A and B, we can follow these steps:
1. Identify the Circles and Their Centers:
- Let the two congruent circles be centered at points O and O'.
- Since the circles are congruent, they have equal radii.
2. Draw the Intersecting Points:
- The circles intersect at points A and B.
3. Draw the Relevant Segments:
- Draw line segments OA, OB, O'A, and O'B.
- Here, OA and O'A are the radii of the first and second circles, respectively, and OB and O'B are also the radii of the circles.
4. Establish Triangle Congruence:
- In triangles OAB and O'AB:
- OA = O'A (both are radii of the circles)
- OB = O'B (both are also radii of the circles)
- AB = AB (common side)
- Therefore, by the Side-Side-Side (SSS) congruence criterion, triangle OAB is congruent to triangle O'AB.
5. Conclude Angle Equality:
- Since triangle OAB is congruent to triangle O'AB, the corresponding angles are equal.
- Hence, angle AOB = angle AO'B.
6. Final Statement:
- Therefore, the statement "angle AOB = angle AO'B" is true.
- Let the two congruent circles be centered at points O and O'.
- Since the circles are congruent, they have equal radii.
- The circles intersect at points A and B.
- Draw line segments OA, OB, O'A, and O'B.
- Here, OA and O'A are the radii of the first and second circles, respectively, and OB and O'B are also the radii of the circles.
- In triangles OAB and O'AB:
- OA = O'A (both are radii of the circles)
- OB = O'B (both are also radii of the circles)
- AB = AB (common side)
- Therefore, by the Side-Side-Side (SSS) congruence criterion, triangle OAB is congruent to triangle O'AB.
- Since triangle OAB is congruent to triangle O'AB, the corresponding angles are equal.
- Hence, angle AOB = angle AO'B.
- Therefore, the statement "angle AOB = angle AO'B" is true.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.320videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
Two circles with centres O and O'are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. prove that OA bisects angle BAC.
 View Solution
View SolutionIn Figure, two congruent circles with centres O and O' intersect at A and B. If ∠AO′B=500, then find ∠APB
View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
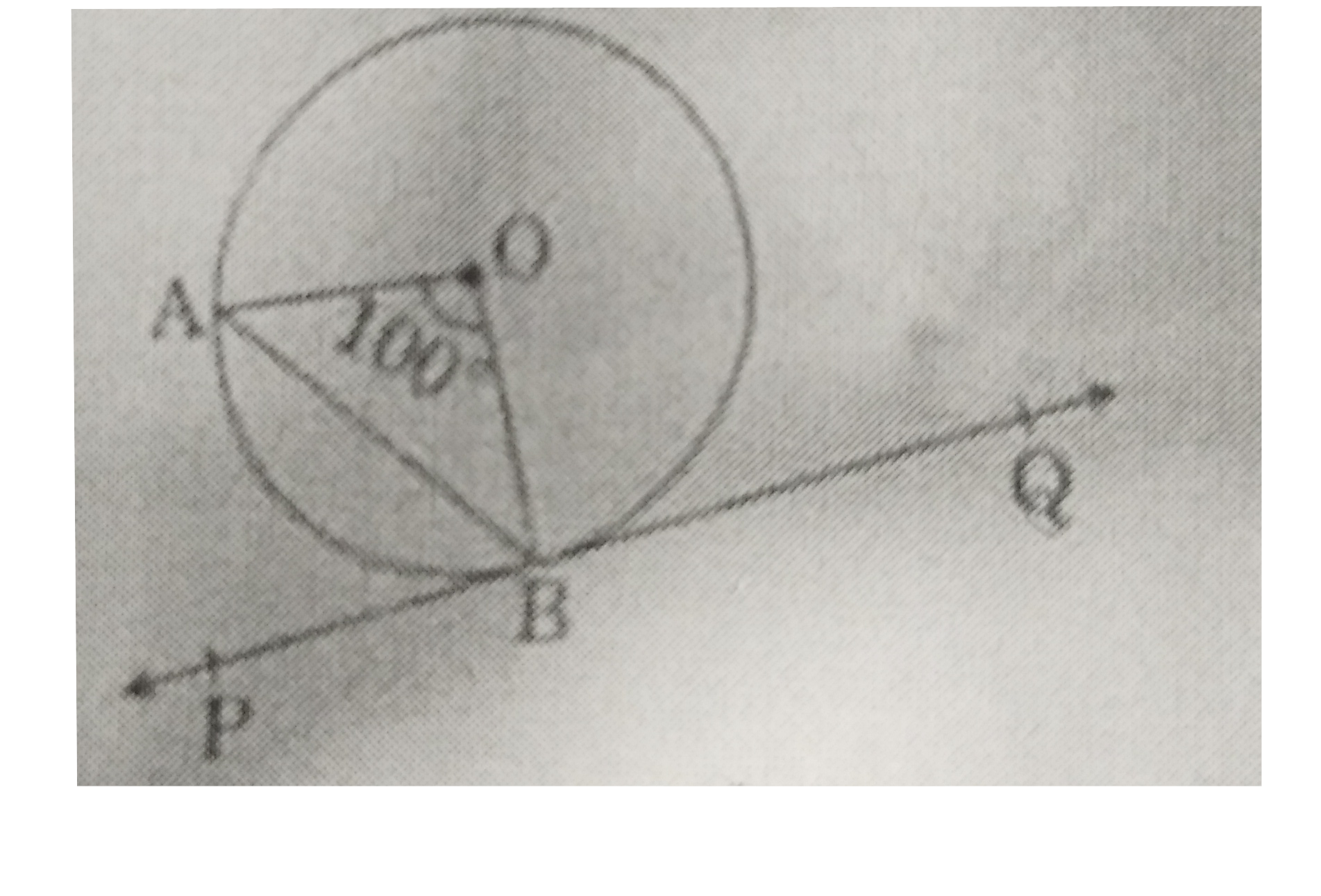 View Solution
View SolutionCircles with centres P and Q intersects at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent, show that : CE = BD.
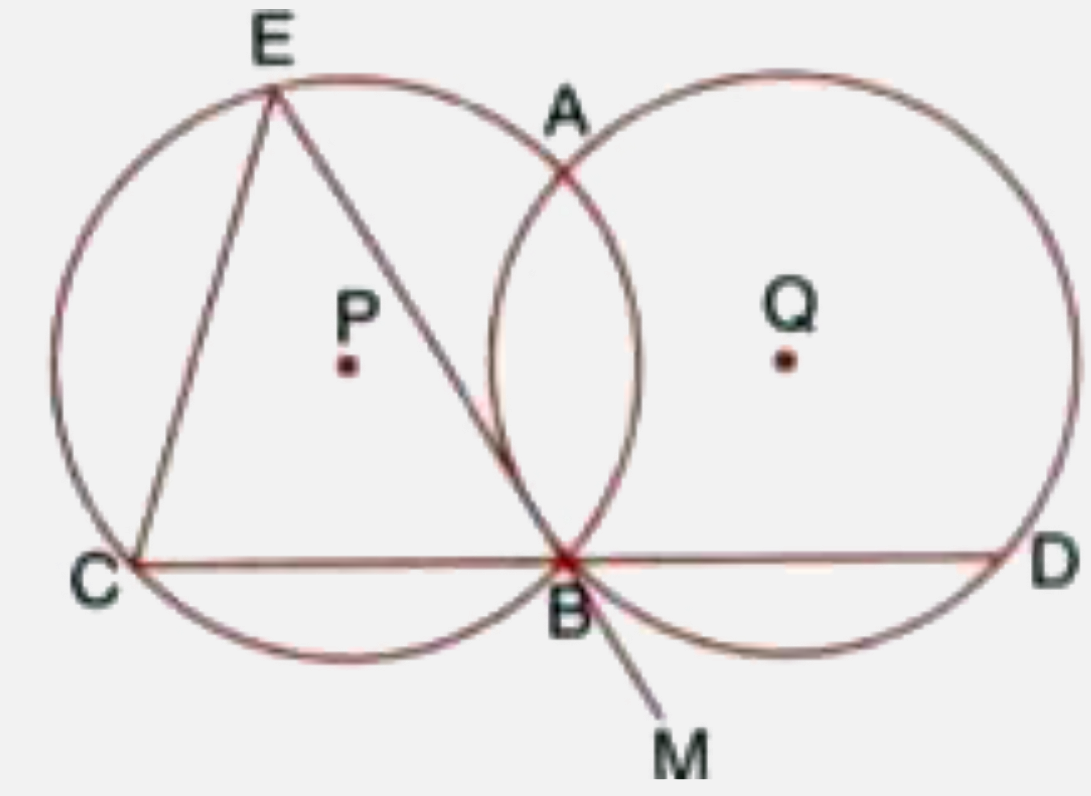 View Solution
View Solution
In the figure shown above, ∠Q measures 70∘ , ¯¯¯¯¯¯PQ≅¯¯¯¯¯¯PR , and ¯¯¯¯¯¯PQ and ¯¯¯¯¯¯PR are tangent to the circle with center O at points A and B . Find , in degrees , the measure of ∠AOB.View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionTwo congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View SolutionTwo circles with equal radii are intersecting at the points (0, 1) and (0,-1). The tangent at the point (0,1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is.
View Solution

