Two tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
PA and PB are tangents to the circle
∴OA⊥PAandOB⊥PB(tangent to the circle is perpendicular to radius at the of contact)
∴∠Aand∠Bare900
In quadrilateral AOBP
∠A+∠O+∠B+∠P=360
0
∴900+∠O+900+∠P=360
^0
∴∠O+∠P=1800
Sum of opposite angles of quadrilateral AOBPis1800
Hence, quadrilateral AOBP is cyclic quadrilateral
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
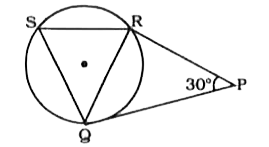 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
A24 cm.B6 cm.C8 cm.DCannot be determined
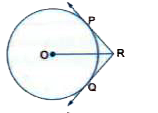
In Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
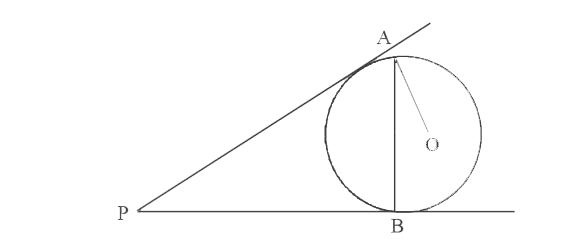
View SolutionIn Fig. 10.60, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN . (FIGURE)
View SolutionIn the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB=115∘, find ∠APO.

View SolutionIn figure, PTandPS are tangents drawn from a point P to a circle with centre at 0. If ∠OPT=35∘, find aandb.
View Solution
