Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a, M and N are the mid-points of AB and BC respectively such that line joining MN intersect the circle at P and Q where P is closer to AB and O is the centre of the circle.
Locus of point of intersection of tangents at A and C is Solution in Punjabi
(a)60∘
(b)90∘
(c)120∘
(d)150∘
The correct Answer is:A
Step by step video solution for Two variable chords AB and BC of a circle x^(2)+y^(2)=a^(2) are such that AB=BC=a, M and N are the mid-points of AB and BC respectively such that line joining MN intersect the circle at P and Q where P is closer to AB and O is the centre of the circle. Locus of point of intersection of tangents at A and C is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - CIRCLE EXERCISE 5: MATCHING TYPE QUESTIONS
4 Videos
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
Similar Questions
If the point (1, 4) lies inside the circle x2+y2−6x−10y+p=0 then p is:
View SolutionFind the radius of the circle x2+y2−4x−6y+12=0
View SolutionOA and OB are two perpendicular straight lines. A straight line AB is drawn in such a manner that OA+OB=8. Find the locus of the mid point of AB.
View SolutionThe value of (300)(3010)−(301)(3011)+(302)(3012)+....+(3020)(3030)
View SolutionFind the modules of 2+3ι
View SolutionTangents PA and PB are drawn to a circle with point P outside the circle,line joining P and centre intersect chord AB at M then,Prove that /_OPA=/_OAM
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The angle between the tangents at A and C is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
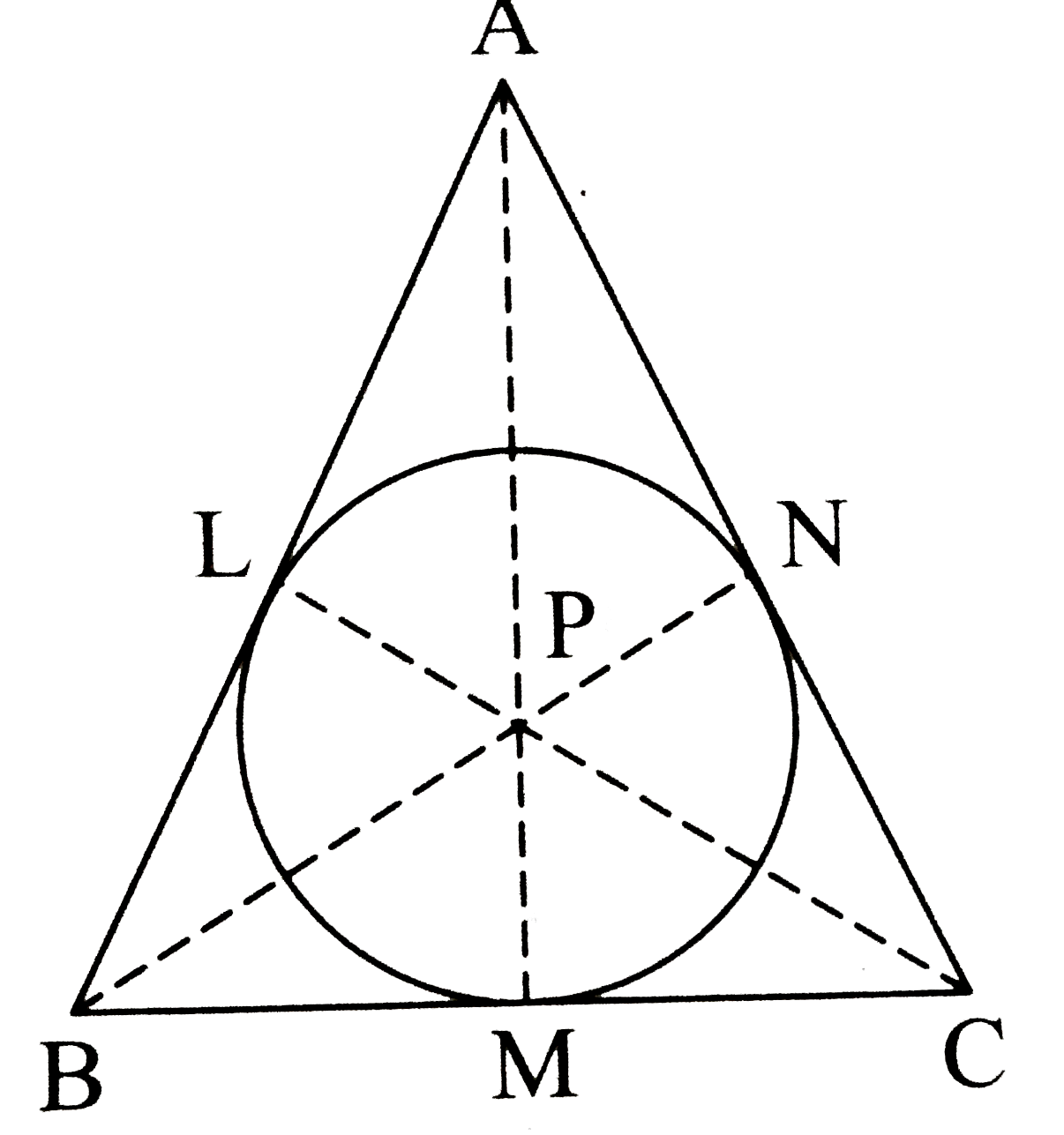
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionAB is a diameter and AC is a chord of the circle with centre at Q. the radius parallel to AC intersect the circle at D. Prove that D is the mid-point of the are BC.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a ,then locus of point of intersection of tangents at A and C is a circle of radius λa, where λ is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
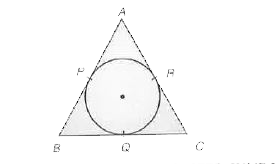
View SolutionIn the given figure, AB, BC and Ac are tangents to the circle at P,Q and R. If AB = AC, show that Q is the mid-point of BC.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View Solution
