Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The angle between the tangents at A and C is Solution in Tamil
90∘
120∘
60∘
150∘
The correct Answer is:3
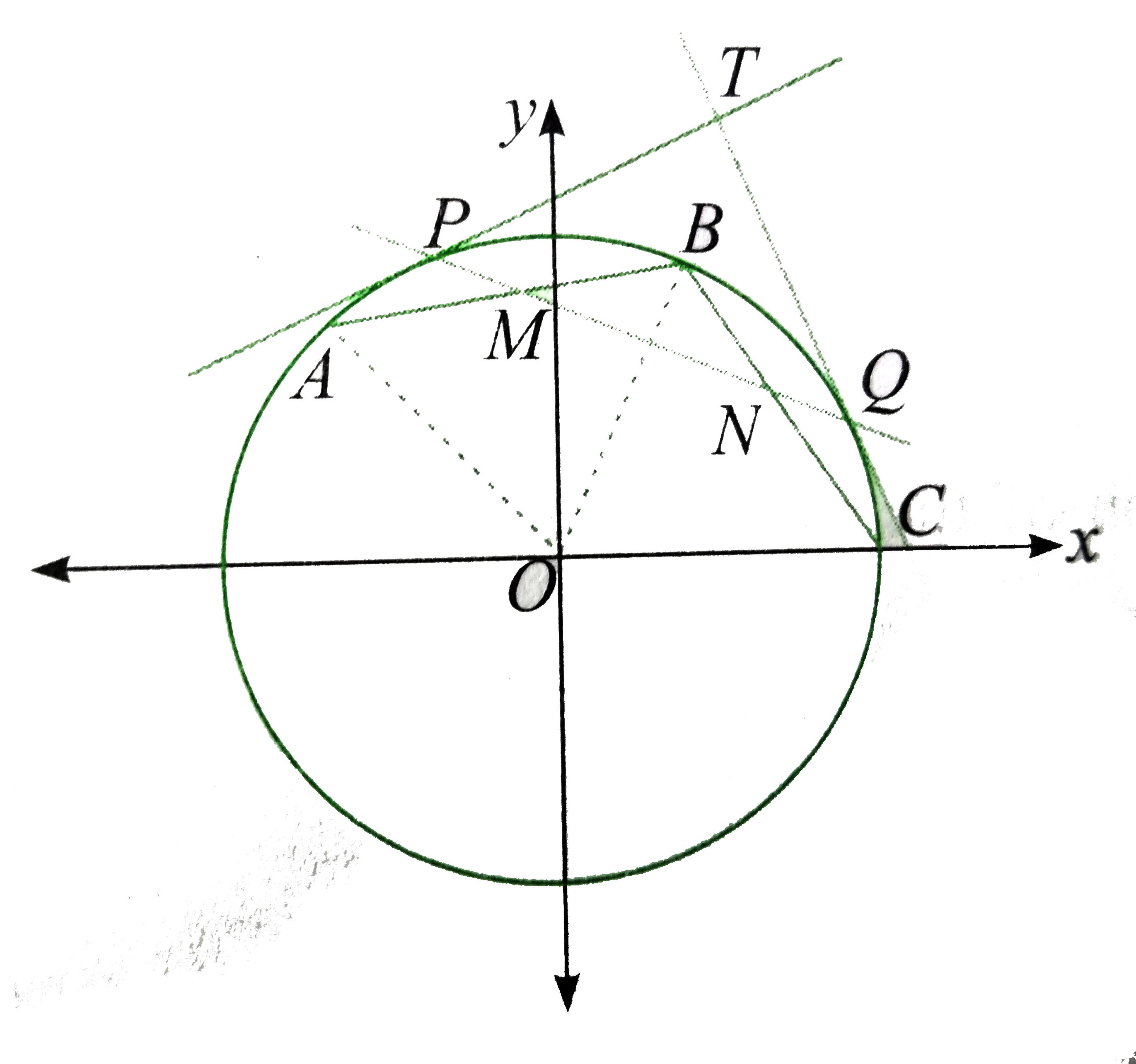
Let T be the point of intersection of tangents .
Since ∠AOC=120∘, the angle between the tangents is 60∘
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)1videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Numerical)18videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
02:55View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2gx+fy+7=0 , then the value of |f+g| is__________
03:43View Solutionabout to only mathematics
05:26View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is01:57View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:27View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
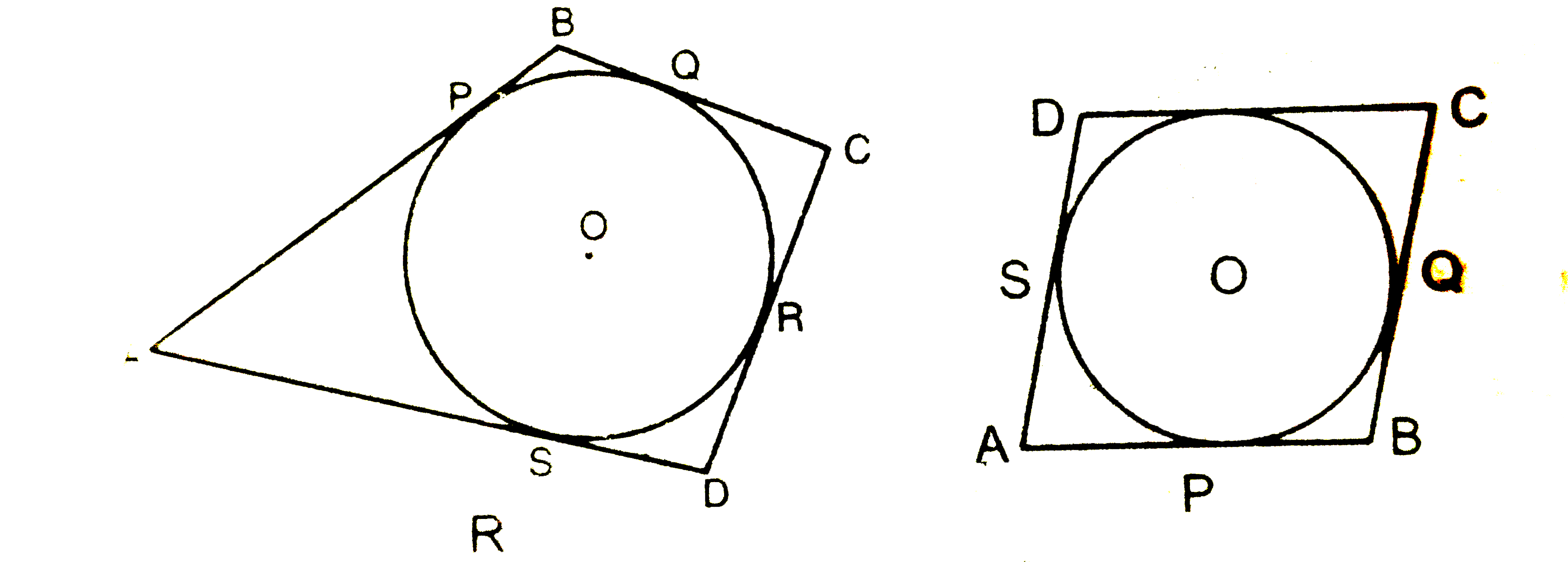
03:00View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
04:26View SolutionAB is a chord of the circle x^(2)+y^(2)=9 .The tangents at A and B intersect at C. If M(1,2) is the midpoint of AB,then the area of triangle ABC is
02:33View SolutionAB, O केंद्र वाले वृत्त की जीवा है । वृत्त पर C बिंदु इस प्रकार है कि OC ⊥ AB और त्रिज्या OC जीवा AB को P पर काटती है । यदि PC = 2 सेमी. और AB = 6 सेमी. हो तो वृत्त का व्यास कितना है ?
04:37View Solutionएक वृत्त, एक चतुर्भुज ABCD की चारों भुजाओं को अन्तः स्पर्श करता है। सिद्ध कीजिए कि-
AB + CD = AD + BC.
(अथवा) आकृति, में एक चतुर्भुज ABCD, O केन्द्र वाले वृत्त के परिगत इस प्रकार बनाई गई है कि भुजाएँ AB, BC, CD, तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R तथा S पर स्पर्श करती हैं। सिद्ध कीजिए कि
AB + CD = BC + DA
 05:04View Solution
05:04View SolutionO केन्द्र के वृत्त की एक जीवा AB है | AB को C तक इस प्रकार बढ़ाया गया है कि BC = OB है | CO को मिलाकर बढ़ाया गया है जो वृत्त पर D पर मिलती हैं |
यदि angleACD=y^(@)"और "angleAOD=x^(@) तो सिद्ध कीजिए x=3y.View Solutionचित्र में वृत्त का केन्द्र O है AB तथा BC दो जिवाएँ इस प्रकार है की ∠ABO=∠CBO सिद्ध करे की AB=CB
 04:38View Solution
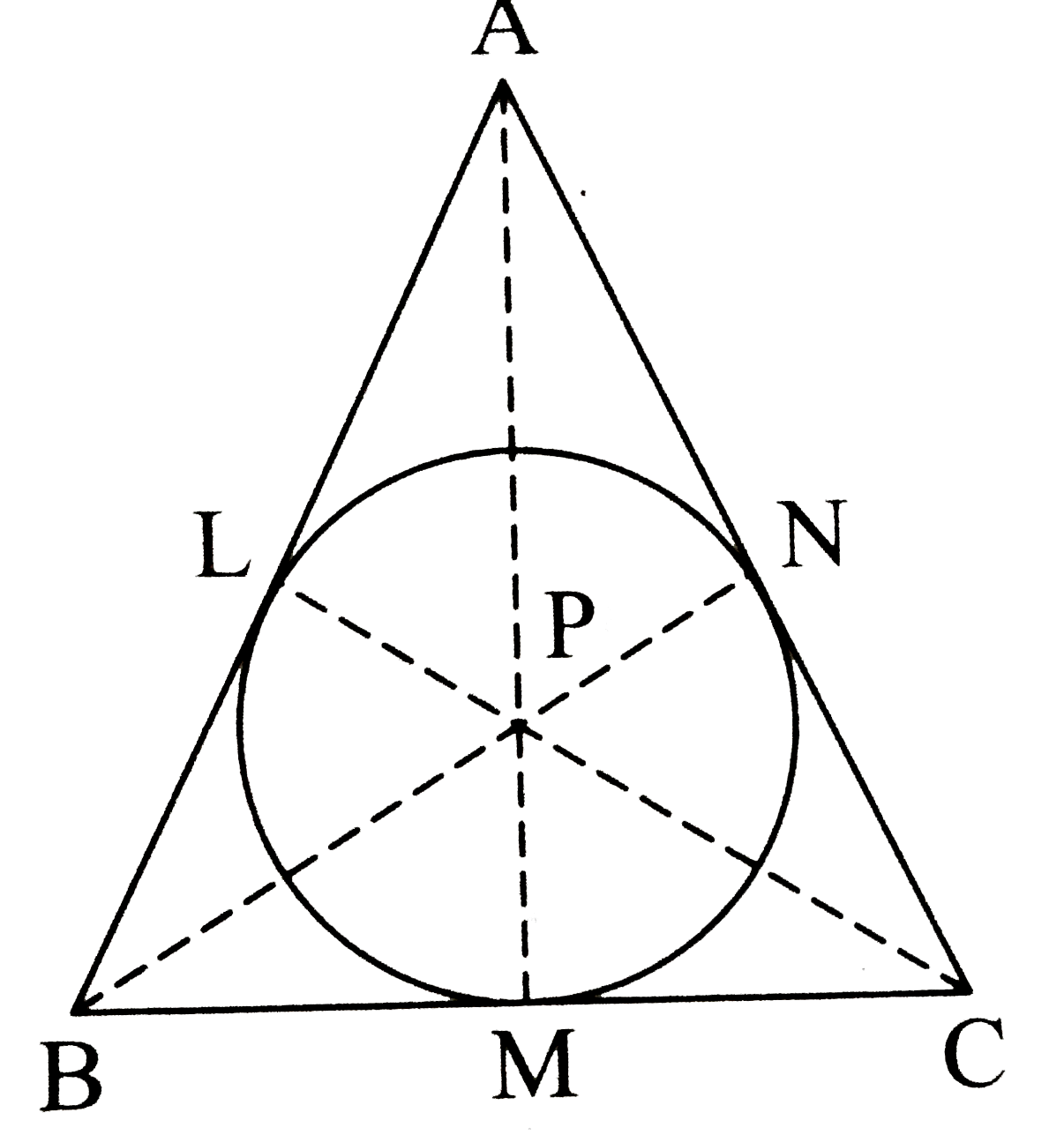
04:38View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
 03:09View Solution
03:09View SolutionA circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
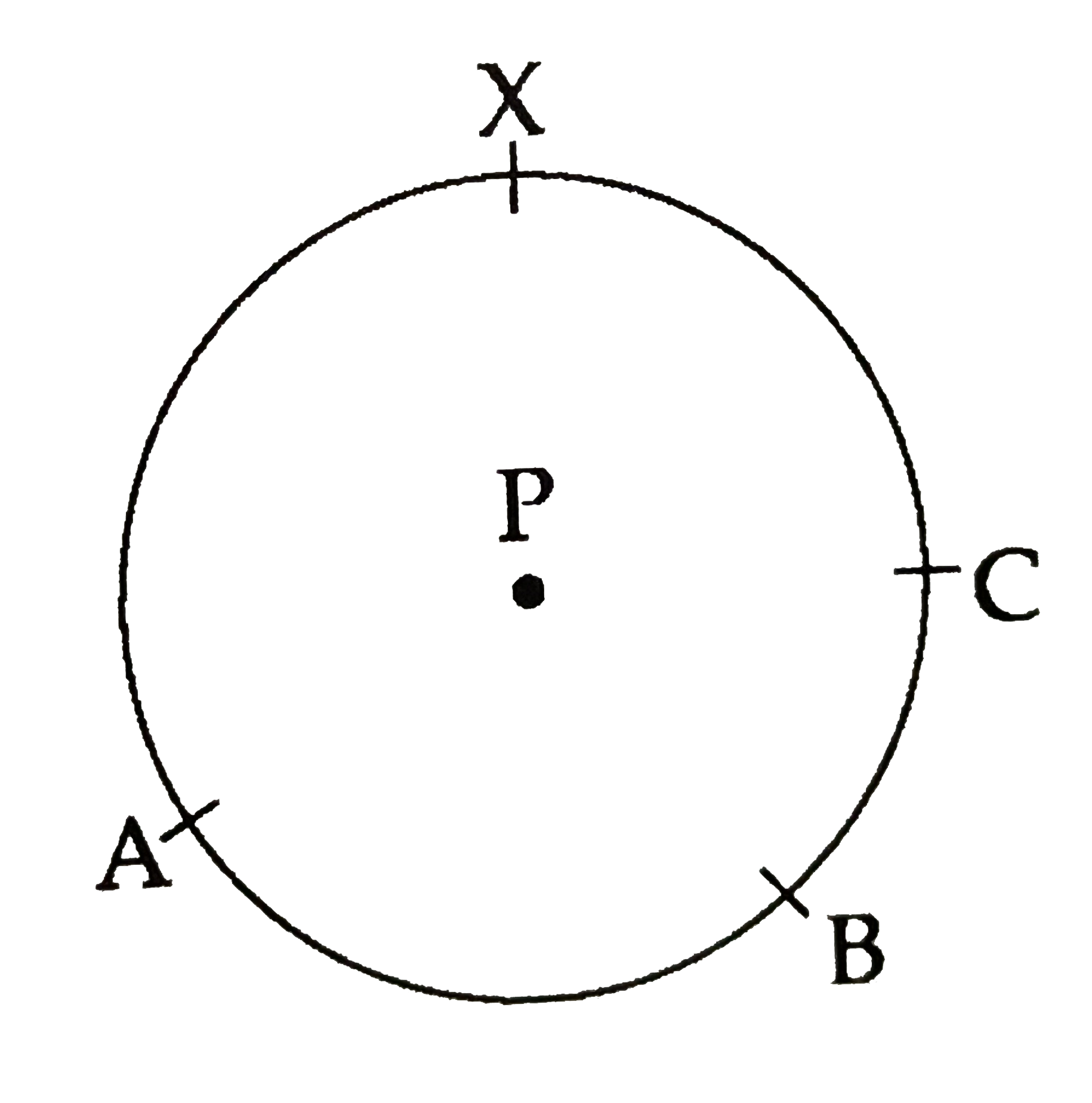 04:59View Solution
04:59View SolutionAB तथा CD एक वृत्त की समान जीवाएं हैं । वृत्त का केंद्र O है। यदि M और N क्रमशः जीवाओं AB तथा CD के मध्यबिंदु हों तो सिद्ध कीजिए कि ∠AMN=∠CNM.
03:01View SolutionIn circle AOD is diameter with centre of circle O and AB,BC,CD are equal chord then angle suntened by chord BC at centre is
03:20View Solution

