Complete Solutions to All Questions of chapter X Boards of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | X Boards |
| 2017 | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
What is the common difference of an A P. in which `a_21-a_7=84`
View SolutionIf a tower 30 m high, casts a shadow `10sqrt3 m` long on the ground, then what is the angle of elevation of the sun ?
View SolutionThe probability of selecting a rotten apple randomly from a heap of 900 apples is 0·18. What is the number of rotten apples in the heap ?
View SolutionFind the value of p, for which one root of the quadratic equation `px^2-14x + 8 = 0` is 6 times the other.
View SolutionWhich term of the sequence `20 ,19 1/4, 18 1/2, 17 3/4,dot` is the first negative term?
View SolutionProve that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
View SolutionIf `(a^2+b^2)x^2+2(ac+bd)x+c^2+d^2=0` has no real root
View SolutionIn an A.P. first term is 5, last term is 45 and sum = 400 . Find the no. of terms and common difference of A.P.
View SolutionOn a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
View SolutionA bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball from the bag is twice that of a red ball, find the number of blue balls in the bag.
View SolutionIn what ratio does the point `(24/11,y)` divide the line segment joining the points P(2, 2) and Q(3, 7) ? Also find the value of y.
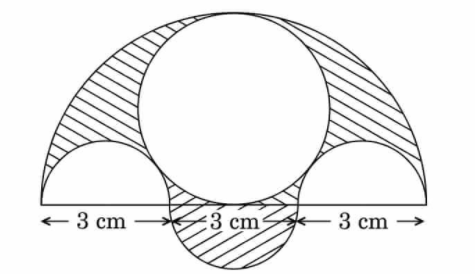
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.
View SolutionWater in a canal, 2·4 m wide and 1·8 m deep, is flowing with a speed of 50 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation ?
View SolutionThe slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
View SolutionSolve for `x` : `1/(x+1)+3/(5x+1)=5/(x+4), x != -1,-1/5,-4`
View SolutionTwo taps running together can fill a tank in `3(1/13)` hours. If one tap takes 3 hours more than the other to fill the tank, then how much time will each tap take to fill the tank ?
View SolutionIf the ratio of the sum of first n terms of two AP's is (7n+1) : (4n + 27), then find the ratio of their mth terms.
View Solutionabout to only mathematics
View Solution`X Y`and `Xprime Yprime`are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting `X Y`at A and `XprimeYprime`at B. Prove that `/_A O B\ =\ 90^0`
View SolutionAn aeroplane flying at a height 300 metre above the ground passes vertically above another plane at an instant when the angles of elevation of the two planes from the same point on the ground are `60^@` and `45^@` respectively. Then the height of the lower plane from the ground in metres is
View SolutionIf two different dice are rolled together, the probability of getting an even number of both dice is
View SolutionQ. For what value of k will k+9, 2k-1 and 2k+7 are the consecutive terms of an A.P.
View SolutionA ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
View SolutionA card is drawn at random from a well shuffled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen and (2) a face card
View SolutionIf `-5` is a root of the quadratic equation `2x^2+p x-15=0` and the quadratic equation `p(x^2+x)+k=0` has equal roots, find the value of `kdot`
View SolutionLet P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionThe fourth term of an A.P is zero. Prove that the 25th term is triple its 11th term
View SolutionIn the given figure, from an external point P,two tangents PT and PS are drawn to a circle with centre O and radius r.If OP=2r, show that `/_OTS=/_OST=30^@`
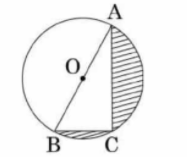
View SolutionIn fig. O is the center of a circle such that diameter AB=13cm and AC= 12 cm. BC is joined. Find the area of the shaded region.
View SolutionIf the point P(x, y) is equidistant from the points A(a + b, b-a) and B(a-b, a + b). Prove that bx = ay.
View SolutionFind the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and `/_A O C"\ "="\ "40o`
View SolutionIf the ratio of the sum of first n terms of two AP's is (7n+1) : (4n + 27), then find the ratio of their mth terms.
View SolutionSolve for `x`:`1/ ((x -1)(x -2))+1/( (x-2)(x-3))=2/ 3', `x is not equal to 1,2,3 .
View SolutionA conical vessel whose internal radius is 5 cm and height 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10cms. Find the height to which the water rises.
View SolutionA sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by `3 5/9 cm`. Find the diameter of the cylindrical vessel.
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as `60^@` and the angle of depression the base of hill as `30^@`. Find the distance of the hill from the ship and the height of the hill.
View SolutionThree different coins are tossed together. Find the probability of getting (1) exactly 2 heads (2) atleast 2 heads
View SolutionDraw a pair of tangent to a circle of radius 5 cm which are inclined to each other at an angle of `60^@`. Give steps of construction.
View Solution. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of `(DO')/(CO)`.
View SolutionSolve for x :`1/(x+1) +2/(x+2)=4/(x+4)`
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is `60^@`.From a point y 40 m vertically above X, the angle of elevation the top Q of tower is `45^@`.Find the height of the tower PQ and the distance PX.(Use `sqrt3=1.73`)
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is `60^@`.From a point y 40 m vertically above X, the angle of elevation the top Q of tower is `45^@`.Find the height of the tower PQ and the distance PX.(Use `sqrt3=1.73`)
View SolutionThe houses of a row are numbered from 1 to 49. Show that there is a value of `x` such that the sum of the numbers of the houses preceding the house numbered `x` is equal to the sum of the no. of the houses following it. Find the value of the x.
View SolutionA number x is selected at random from the numbers 1, 4, 9, 16 and another number y is selected random from the numbers 1, 2, 3, 4. Find the probability that the value of xy is more than 16.
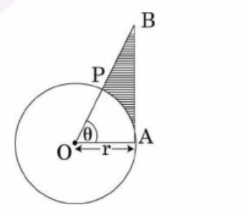
View SolutionIn the given figure, is shown a sector OAP of a circle with centre 0, containing ` /_ theta`. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is `r[tan theta + sec theta + pi theta/180 - 1]`
View SolutionA motor boat whose speed is 24 km/hr in still water takes 1 hr more to go 32 km upstream than to return downstream to the same spot. Find the speed of the stream.
View SolutionIf the quadratic equation ` p x^2 - 2 sqrt(5) + 15 = 0` has two equal roots, then find value of p.
View SolutionA tower AB is 20 m high and BC is its shadow on the ground `20sqrt 3` m long. Find the Sun’s elevation.
View SolutionTwo different dice are tossed together, Find the probability that the product of the two numbers on the top of the dice is 6.
View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O. If `/_PRQ =120^@` , then prove that OR= PR+ RQ
View SolutionSolve the quadratic equation `4x^2+4bx-(a^2-b^2)=0`
View SolutionThe points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B, Find the values of P.
View SolutionFind the relation between x and y if the points `A(x, y), B(-5, 7) and C(-4, 5)` are collinear.
View SolutionThe 14th term of an A.P. is twice its 8th term. If its 6th term is -8, then find the sum of its first 20 terms.
View SolutionSolve for x `sqrt3x^2-2sqrt(2)x-2sqrt3=0`
View SolutionThe angle of elevation of an aeroplane from a point P on the ground is `60^@`. After a flight of 15 seconds, the angle of elevation changes to `30^@`. If the aeroplane is flying at a constant height of `1500 sqrt3` m, find the speed of the aeroplane
View SolutionIf A and B are `(2,""2)" "a n d" "(2,""4)` , respectively, find the coordinates of P such that `A P=3/7 A B` and P lies on the line segment AB.
View SolutionThe probability of selecting a green marble at random from a jar that contains green,white and yellow marble is 1/3. The probability of selecting a white marble random from the jar is 2/9.If the jar contains 8 yellow marbles, find the total numbers of marbles in the jar
View SolutionDue to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost, If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs 100 per sq. m, find the amount the associations will have to pay. What values are shown by these associations [Use `pi=22/7`]
View SolutionA hemisphereical bowl of internal diameter 36cm contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3cm and height 6cm. How many bottles are required to empty.
View SolutionThe diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
View SolutionFind the 60th term of the AP 8, 10, 12, ……., if it has a total of 60 terms and hence find the sum of its last 10 terms.
View SolutionA train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that tangent drawn at the mid point of the are of a circle is pallelar to the chord joing the ends of point of the are
View SolutionThe angle of elevation of the top of a tower from a point A on the ground is `30^0dot` On moving a distance of 20 metres towards the foot of the tower to a point B the angle of elevation increases to `60^0dot` Find the height of the ttower and the distance of the tower from the point A.
View SolutionA card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is (a) a spade or an ace (b) a black king (c) neither a jack nor a king (d) either a king or a queen.
View SolutionFind the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
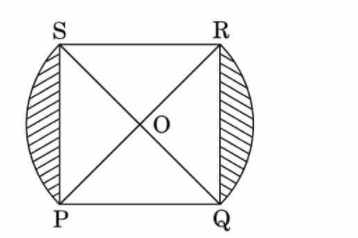
View SolutionIn the following figure, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its diagonals. Find the total area of the two flower beds (shaded parts).
View SolutionIf `x + k` is the GCD of `x^2 -2x - 15` and `x^3 + 27`, find the value of k
View Solutionsolve for x and y, `x+ (6/y)=6,3x-(8/y)=5`
View SolutionFind the sum of first 25 terms of an A.P. whose nth term is `1- 4n`
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that `A E^2+B D^2=A B^2+D E^2` .
View SolutionFind the mean of the following frequency distribution: Classes: 0-20 20-40 40-60 60-80 80-100 Frequency: 15 18 21 29 17
View SolutionCards marked with numbers 3, 4, 5, ......, 50 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that number on the drawn card is dividing by 7.
View SolutionA washing machine is available for Rs. 13,500 cash or Rs. 6,500 as cash down payment followed by three monthly instalments of Rs. 2,500 each. Find the rate of interest charged under instalment plan.
View SolutionSolve the following system of equations graphically : `2x + 3y = 8 ; x + 4y = 9`
View SolutionSimplify: `x/(x-y)-y/(x+y)-(2x y)/(x^2-y^2)`
View SolutionWhich term of the AP: 3, 15, 27, 39, . . . will be 132 more than its `54^(t h)` term?
View SolutionIn a fig. PA is a tangent to the circle. PBC is a secant & AD bisects angle BAC. Show that triangle PAD is an isosceles triangle.Also show that `/_CAD=1/2(/_PBA-/_PAB)`
View SolutionDraw a triangle PQR with base QR = 6 cm, vertical angle P = 60° and median through P to the base is of length 4.5 cm.
View SolutionA toy is in the form of a cone mounted on a hemisphere of same radius 7 cm. If the total height of the toy is 31cm, find the total surface area.
View SolutionThe enrolment of a secondary school in different classes is given below : Class VI VII VIII IX X Enrolment 600 500 400 700 200. Draw a pie chart to represent the above data.
View SolutionA bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
View Solution`(cosA)/(1-tanA)+(sinA)/(1-cotA)=sinA+cosA`
View SolutionShow that the points (7, 10), (-2, 5), and (3, -4) are the vertices of an isosceles right triangle.
View SolutionIn what ratio does the line x -y - 2 = 0 divides the line segment joining (3, -1) and (8, 9) ?
View SolutionA man borrows money from a finance company and has to pay it back in two equal half-yearly instalments of Rs. 7,396 each. If the interest is charged by the finance company at the rate of 15% per annum, compounded semi-annually, find the principal and the total interest paid.
View Solution`If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionProve that the sum of opposite pair of angles of a cyclic quadrilateral is `180^@`
View SolutionThe difference of two numbers is 5 and the difference of their reciprocals is `1/10` Find the numbers.
View SolutionThe difference of two numbers is 5 and the difference of their reciprocals is `1/10` Find the numbers.
View SolutionA sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by `3 5/9 cm`. Find the diameter of the cylindrical vessel.
View SolutionA boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of `30^@`. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be `45^@`. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.
View SolutionThe salary of Mrs. Sarita is Rs 32000 per month. `10%` of it is deducted by the employer as provident fund. Of the remaining money, she spends `20%` on house rent, `46%` on food, `14%` on the education of children and `10%` another expenses. Rest she saves. Find :
how much does she save every month.
View SolutionComplete the missing entriesin the following factor tree
View SolutionIf `(x+ p) `is a factor of the polynomial `2x^2 +2px+5x+10`. find p.
View SolutionIf `(x+ p) `is a factor of the polynomial `2x^2 +2px+5x 10`. find p.
View SolutionThe common difference of the AP `1/p,(1-p)/p,(1-2p)/p..........`is
View Solution
All Questions questions and complete solutions for chapter X Boards of X BOARD PREVIOUS YEAR PAPER ENGLISH of Class 10