Complete Solutions to Collision of chapter WORK, ENERGY, POWER AND COLLISION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY, POWER AND COLLISION |
| A2Z | Collision |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
When two bodies collide elastic, then:
View SolutionDuring inclined collision of two particle
View SolutionTwo ball at the same temperature collide which is consved?
View SolutionIn perfectily inelastaic collition the relative velocity of the bodies
View SolutionA body just droppeed from a tower explodes into two placed of equal mass in mid -air which of the following is not posible?
View SolutionAn inelestc ball of mass `m` moves at speed a toward mother ineclasits ball of mass `m` at rest They collide and stick togather both moving at speed is nothing else is known about the condition under which the collision take plane which of the fpllowing statement is the most correct?
View SolutionWhich of the following statement is true concening the elastic collision of two object (It is given that no net external force acts on the system of two object and the do not exen force on each other exept during collision)
View SolutionDuring a collision between a closed system of particle in the absence of exerted force
View SolutionIf `u_(1)` and `u_(2)` be the initial velocity and `v_(1)` and `v_(2)` be the final velocities of the colliding partical then we define coefficient of restitution `e` as:
`e = (v_(1) - v_(2))/(u_(1) - u_(2))`
For perfectly inelastic collision 'e' is
View SolutionA ball of mass `M_(1)` collides elastically and head on with another ball of mass `M_(2)` initially at rest . In which the following cases the transfer of momentum will be maximum?
View SolutionA billiard ball moving with a speed of `5 m//s` collides with an identical ball, originally at rest. If the first ball stop dead after collision, then the second ball will move forward with a speed of:
View SolutionA body is allowed to fall on the ground from a height `h_(1)`. If it is rebound to a height `h_(2)` then the coefficient of restitution is:
View SolutionA ball is let fall from a height `h_(0)`. There are `n` collisions with the earth. If the velocity of rebound after `n` collision is `v_(n)` and the ball rises to a height `h_(n)` then coefficient of restitution `e` is given by
View SolutionA body `X` with a momentum `p` collides with another identical stationary body `Y` one dimensionally. During the collision, `Y` gives an impulse `J` to body `X`. Then coefficient of restitution is
View SolutionA pendulum consists of a wooden bob of mass `m` and of length `L`. A bullet of mass `m_(1)` is fired towards the pendulum with a speed `v_(1)`. The bullet emerges out of the bob with a speed `v_(1)//3` and the just completes motion along a vertical circle. Then `v_(1)` is:
View SolutionTwo pendulum each of length `l` are initial situated as shown in figure. The first pendulum is released and strikes the second . Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the center of mass rise after the collision?
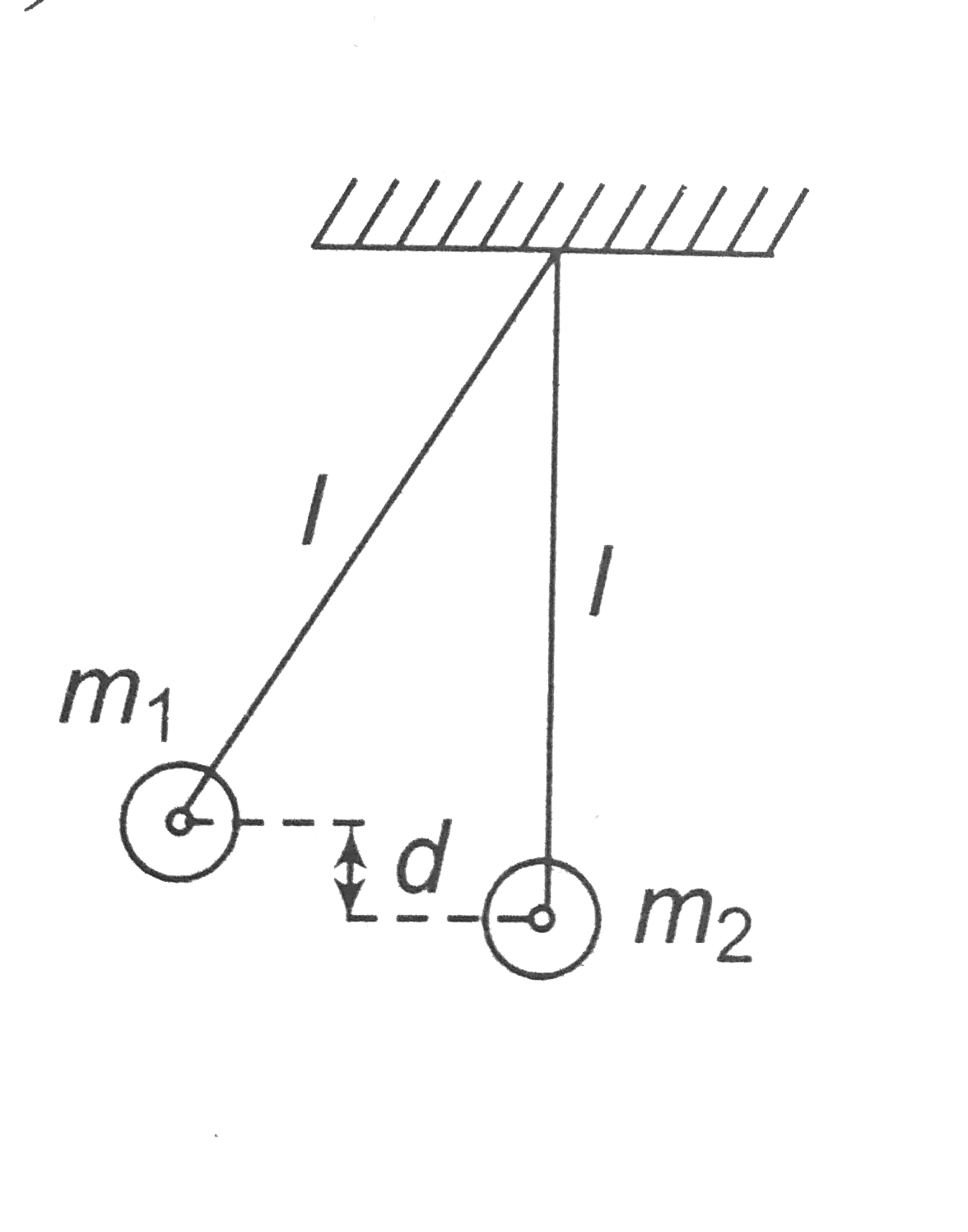
View SolutionA mass 'm' moves with a velocity 'v' and collides inelastieally with another identical mass . After collision the `1^(st)` mass moves with velocity `v/sqrt3` in a direction perpendicular to the initial direction of motion. Find the speed of the `2^(nd)` mass after collision.
`undersetunderset ((before),(collision))(m)(*rarr) underset(m)* uparrow v//sqrt3 underset((after),(collision):)`
View SolutionA ball is projected vertically down with an initial velocity from a height of `20 m` onto a horizontal floor. During the impact it loses `50%` of its energy and rebounds to the same height. The initial velocity of its projection is
View SolutionA partical falls from a height `h` upon a fixed horizontal plane and rebounds. If `e` is the coefficient of restitution, the total distance travelled before rebounding has stopped is
View SolutionThe bob `A` of a simple pendulum is released when the string makes an angle of `45^(@)` with the vertical. It hits another bob `B` of the same meterial and same mass kept at rest on the table. If the collision is elastic, then

View SolutionTwo particle moving in the same direction with speeds `4 m//s` and `2m//s` collide elastically (the collision being head on). After collision , the velocity of first particle becomes `3 m//s` in the same direction . The velocity of the second should be
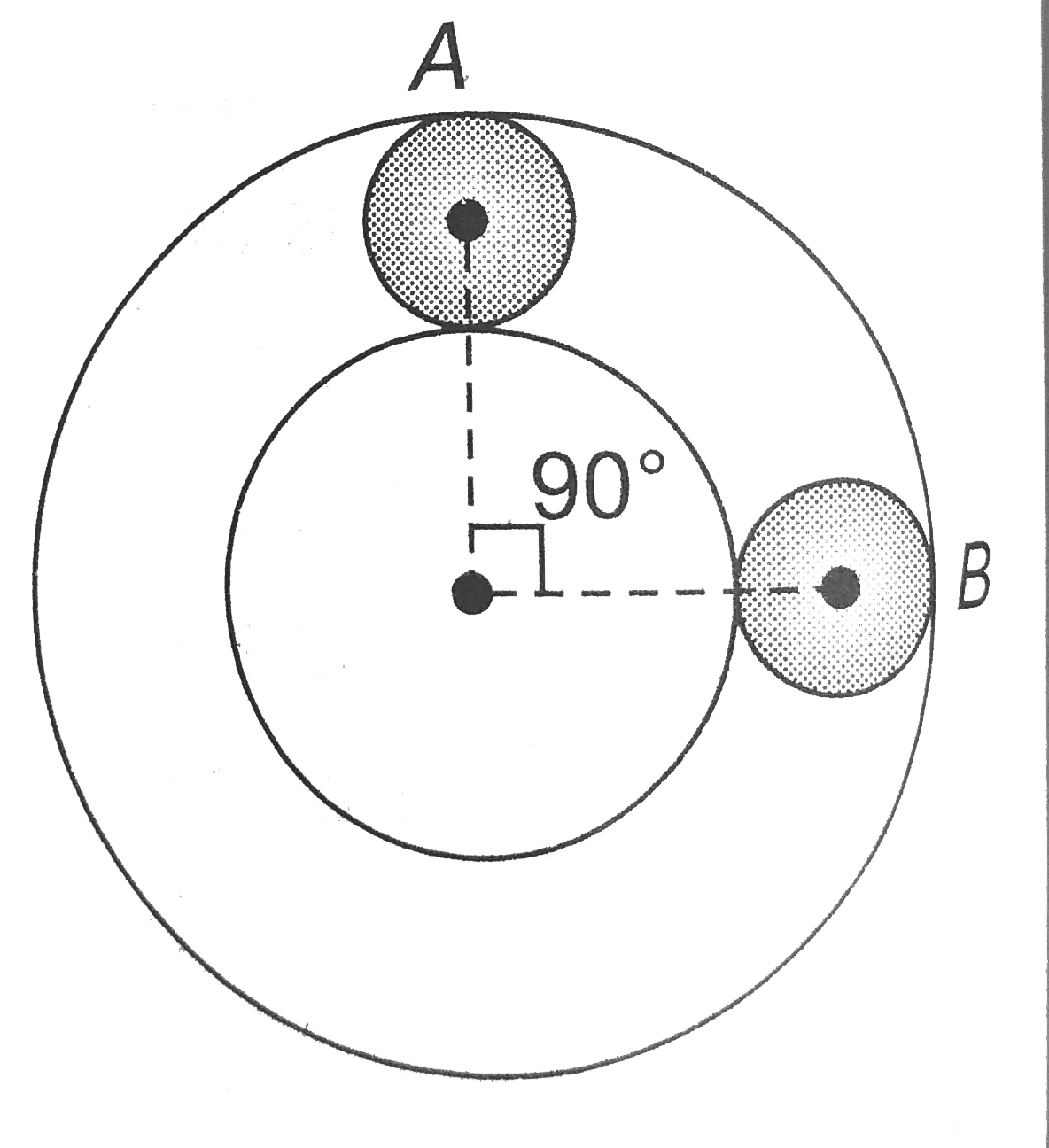
View SolutionBody `A `of mass `m` and `B` of mass `3m` move towards each other with velocities `V and 2 V` respectivally from the positions as shown , along a smooth horizontal circule track of redius `r`. After the first elastic collision , they will collide again after the time:
View SolutionA ball of mass `m` is moving normally towards a walll of mass `M(gt gt m)` with the velocity `4 m//s`. The wall is also moving. After striking elastically with the wall , velocity of ball becomes `8 m//s`. Find the speed of the wall:
View SolutionThe velocity vector of a sphere after it hits a vertical wall which is pallel to `hatj` is `(-hati + 3hatj)` on a smooth horizontal surface. The coefficient of restitution between ball and wall is `(1//2)`. Final the velocity vector of sphere immediately before collision.
View SolutionA partical of mass `m_(1)` collides head on with a stationary partical of mass `m_(2)`. If `(m_(1))/(m_(2)) gt e` where `e` is the coefficient of restitution, then :
View SolutionA ball of mass `1 kg` strikes a heavy platform, elastically, moving upwards with a velocity of `5 m//s`. The speed of the ball just before the collision is `10 m//s` downwards. Then the impulse imparted by the platform on the ball is :-
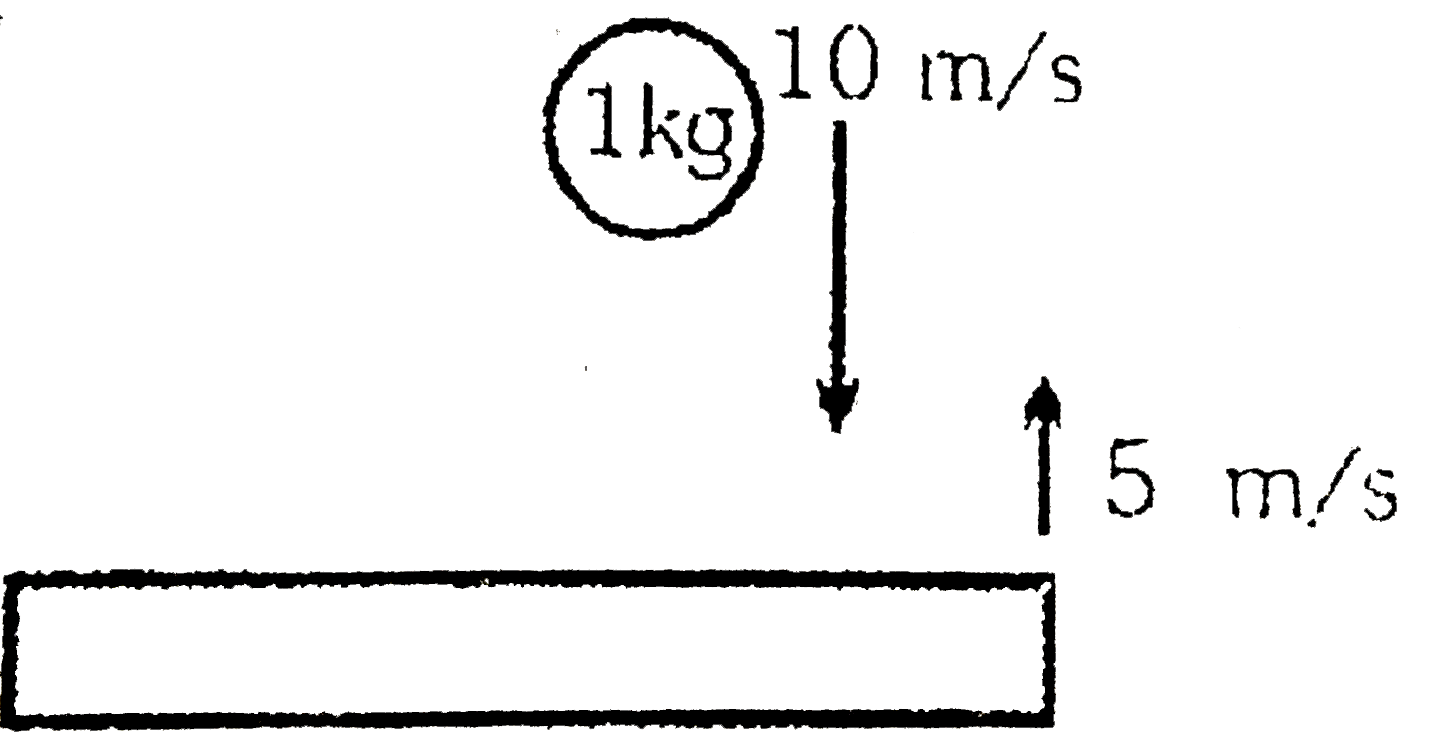
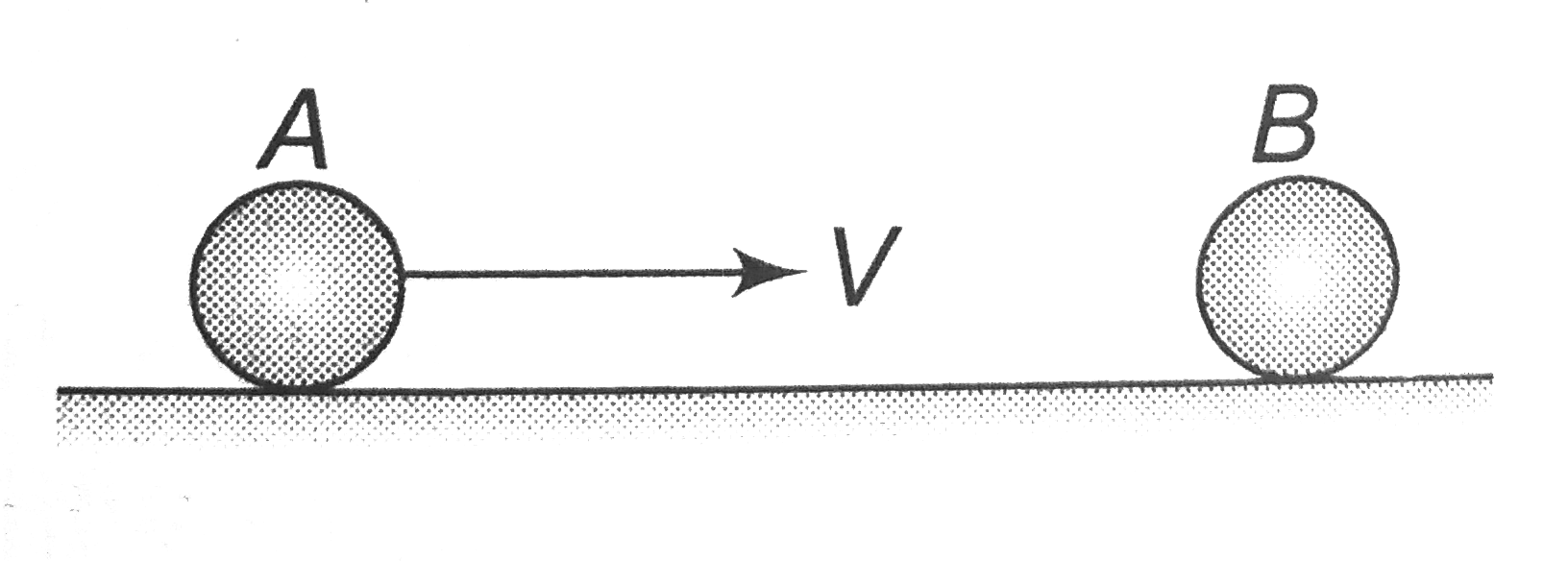
View SolutionThe sphere `A` of mass `m_(1)` moves with velocity `V` on a frictionless horizontal surface and strikes with sphere `B` of mass `m_(2)` at rest. The sphere `A` comes back with speed `V//10`. Choose the correct option.
View SolutionA sphere `A` of mass `m` moving with a velocity hits another stationary sphere `B` of same mass. If the ratio of the velocity of the sphere after collision is `(v_(A))/(v_(B)) = (1 - e)/(1 + e)` where `e` is the cofficient of restitution, what is the initial
velocity of sphere `A` with which it strikes?
View SolutionA ball strickes a horizontal floor at `45^(@). 25%` of its kinetic energy is lost in collision. Find the coefficient of restitution.
View Solution`N` identical balls are placed on a smooth horizontal surface. An another ball of same mass collides elastically with velocity `u` with first ball of `N` balls. A process of collision is thus started in which first ball collides with second ball and the with the third ball and so on. The coefficient of restitution for each collision is `e`. Find the speed of `Nth` ball.
View SolutionA plank of mass `m` moving with a velocity `v` along a frictionless horizontal track and a body of mass `m//2` moving with `2v` collides with plank elastically. Final speed of the plank is:
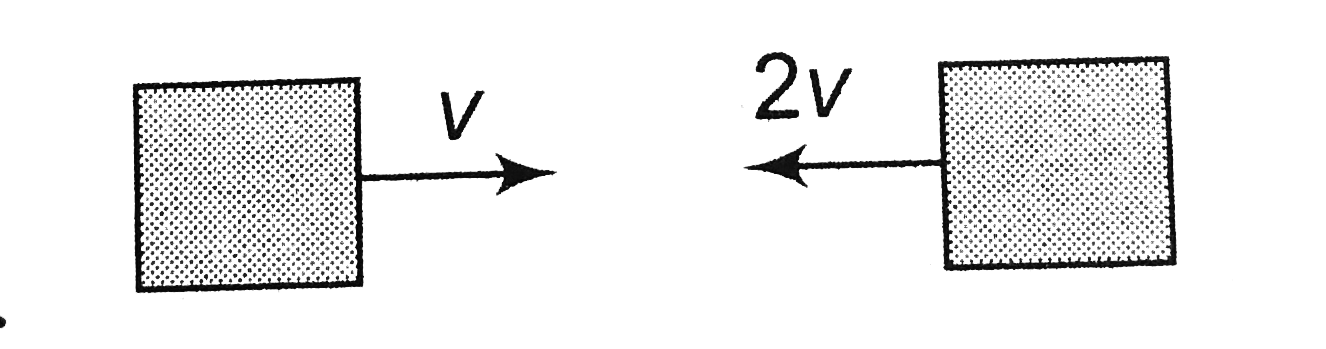
View Solution
Collision questions and complete solutions for chapter WORK, ENERGY, POWER AND COLLISION of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS WORK, ENERGY, POWER AND COLLISION
- AIIMS Questions
- Assertion Reasoning
- Chapter Test
- Circular Motion In Vertical Plane
- Collision
- Concept Of Work Done
- Conservation Of Mechanical Energy And Linear Momentum
- Mechanical Power
- NEET Questions
- Potential Energy, Conservative And Non-Conservative Forces
- Problems Based On Mixed Concepts
- Work-Energy Theorem