Complete Solutions to Centre Of Mass of chapter ROTATIONAL DYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL DYNAMICS |
| A2Z | Centre Of Mass |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
The motion of the centre of mass of a system of two particles is unaffected by their internal forces.
View SolutionTwo bodies
View SolutionThe position of center of mass of a system of particles does not depend upon the
View SolutionTwo bodies
View SolutionThree identical particle each of mass
View SolutionTwo particles of equal mass have velocities
View SolutionThe centre of mass of a system of two particle of masses
View SolutionTwo particles of mass
View SolutionFour particle of masses
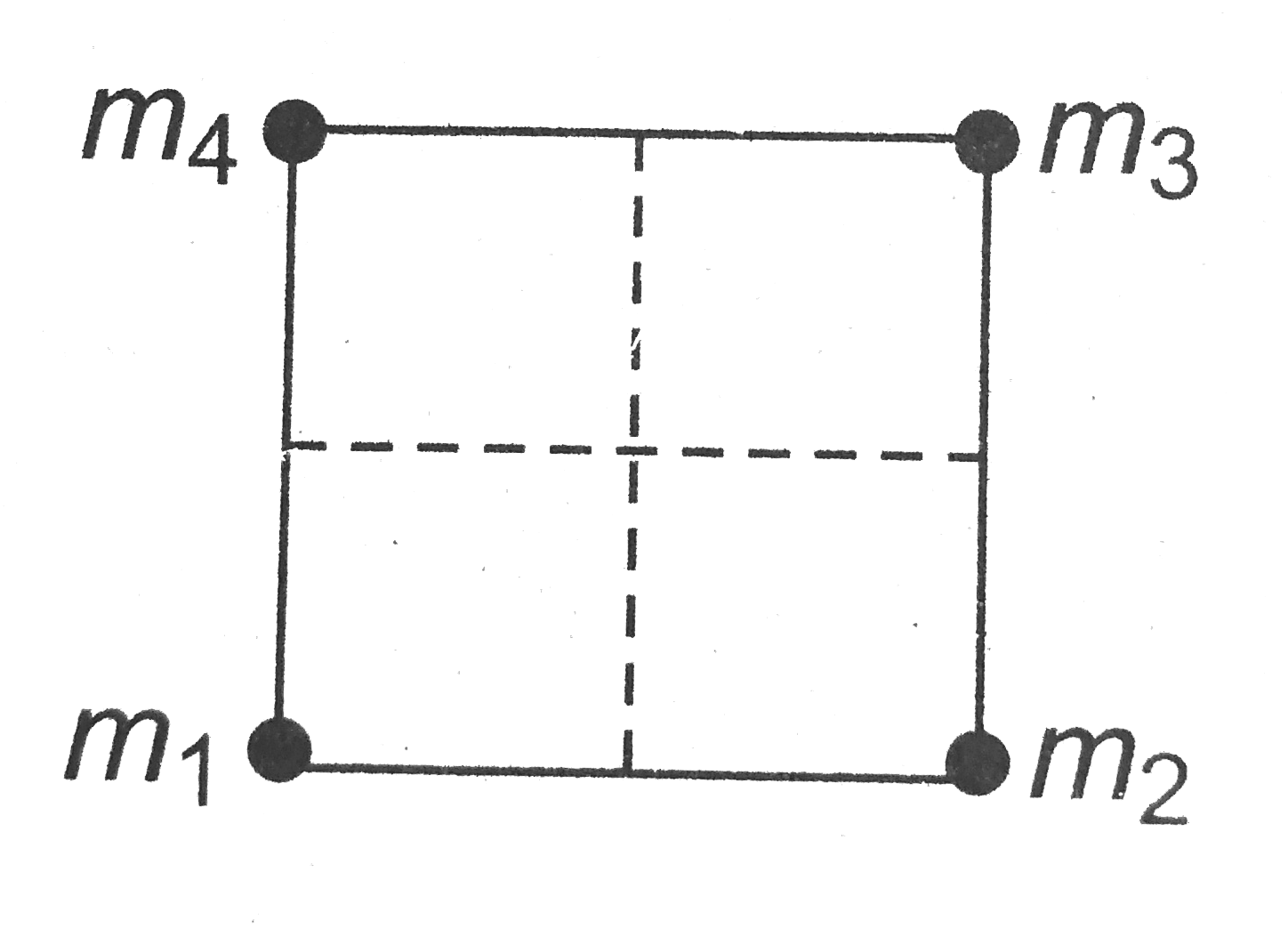
View SolutionThree particles of masses
View SolutionCentre of mass of three particles of masses
View SolutionA square of side
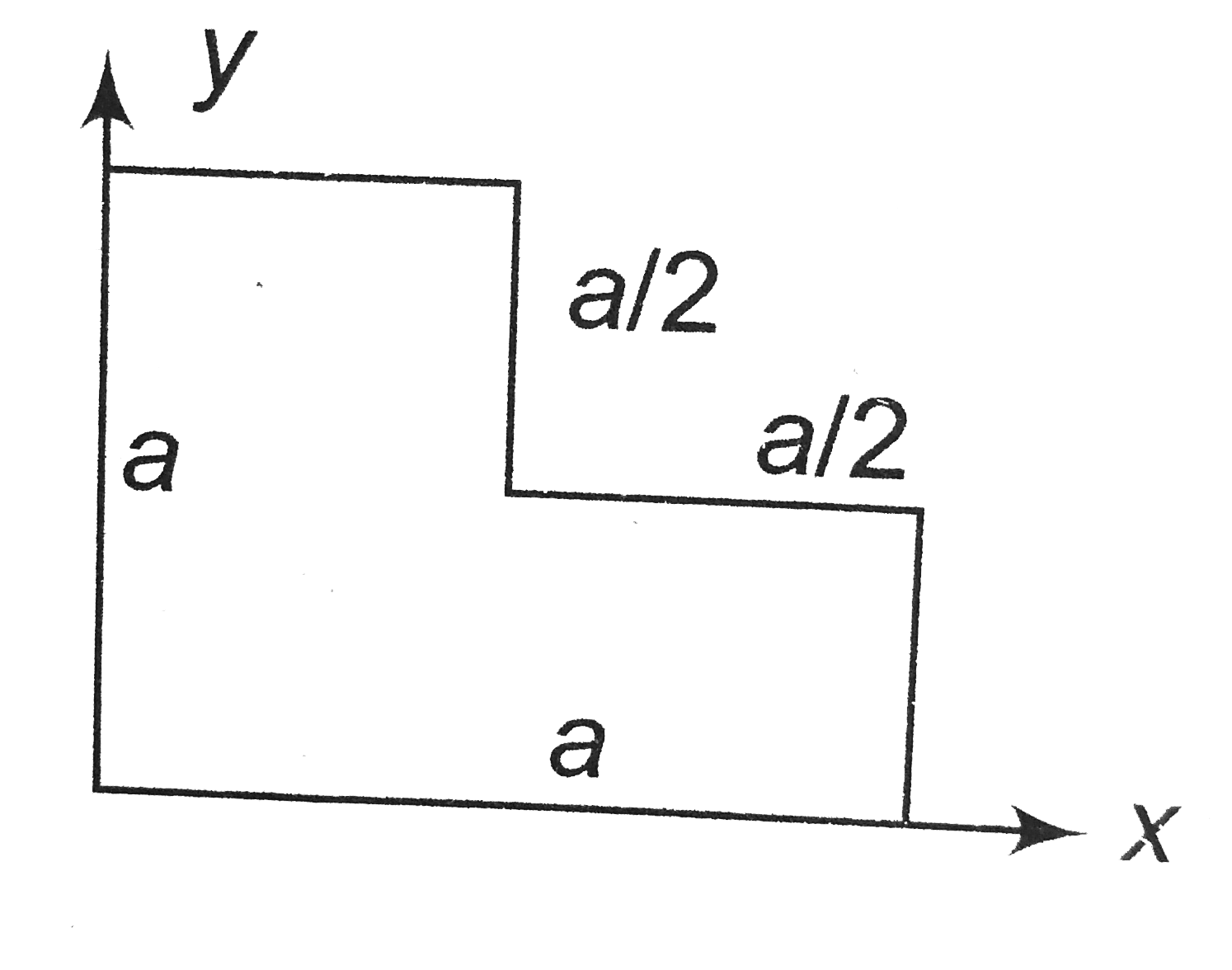 .
.
View SolutionThree identical spheres each of radius
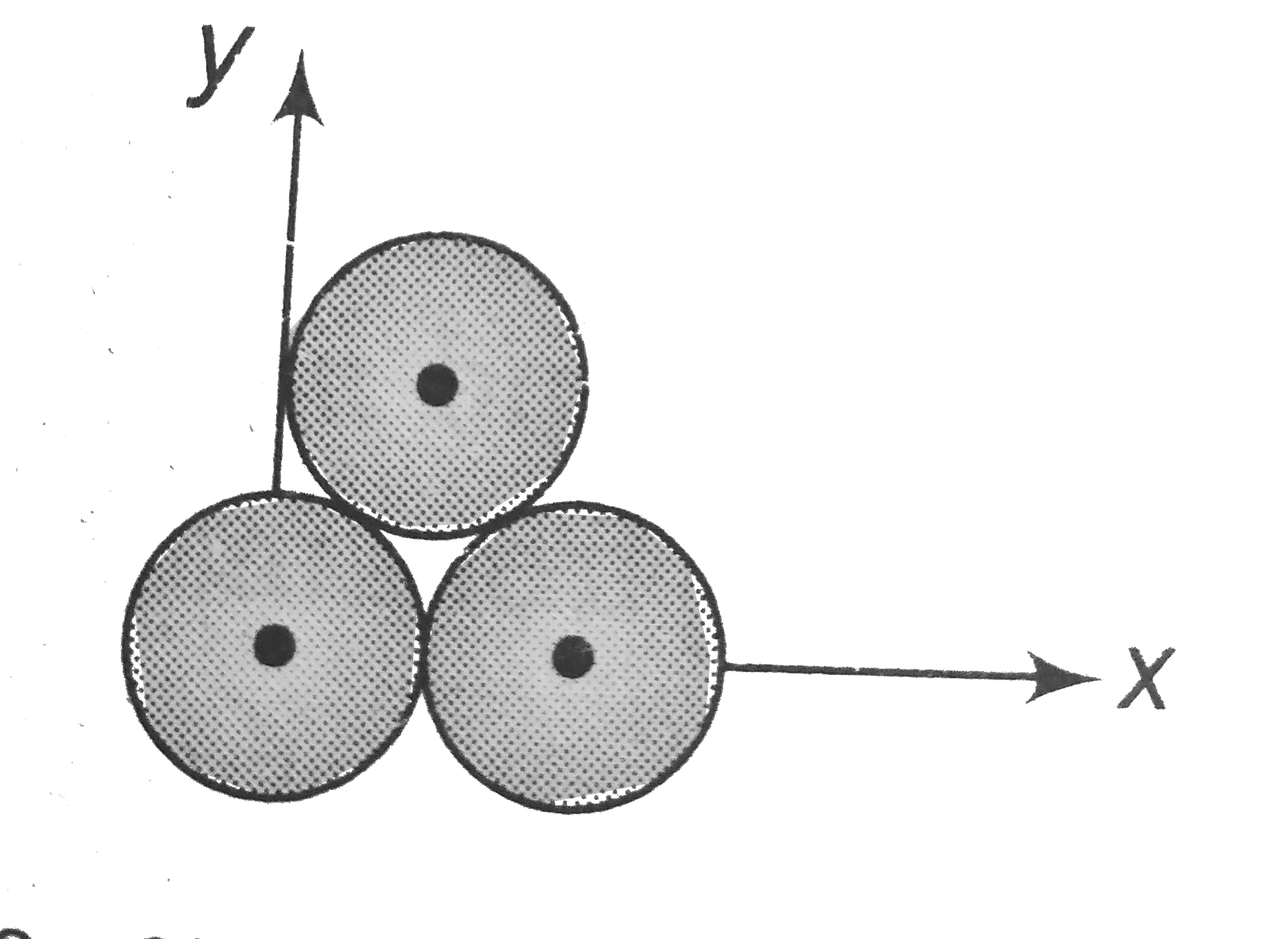 .
.
View SolutionFive uniform circular plates, each of diameter
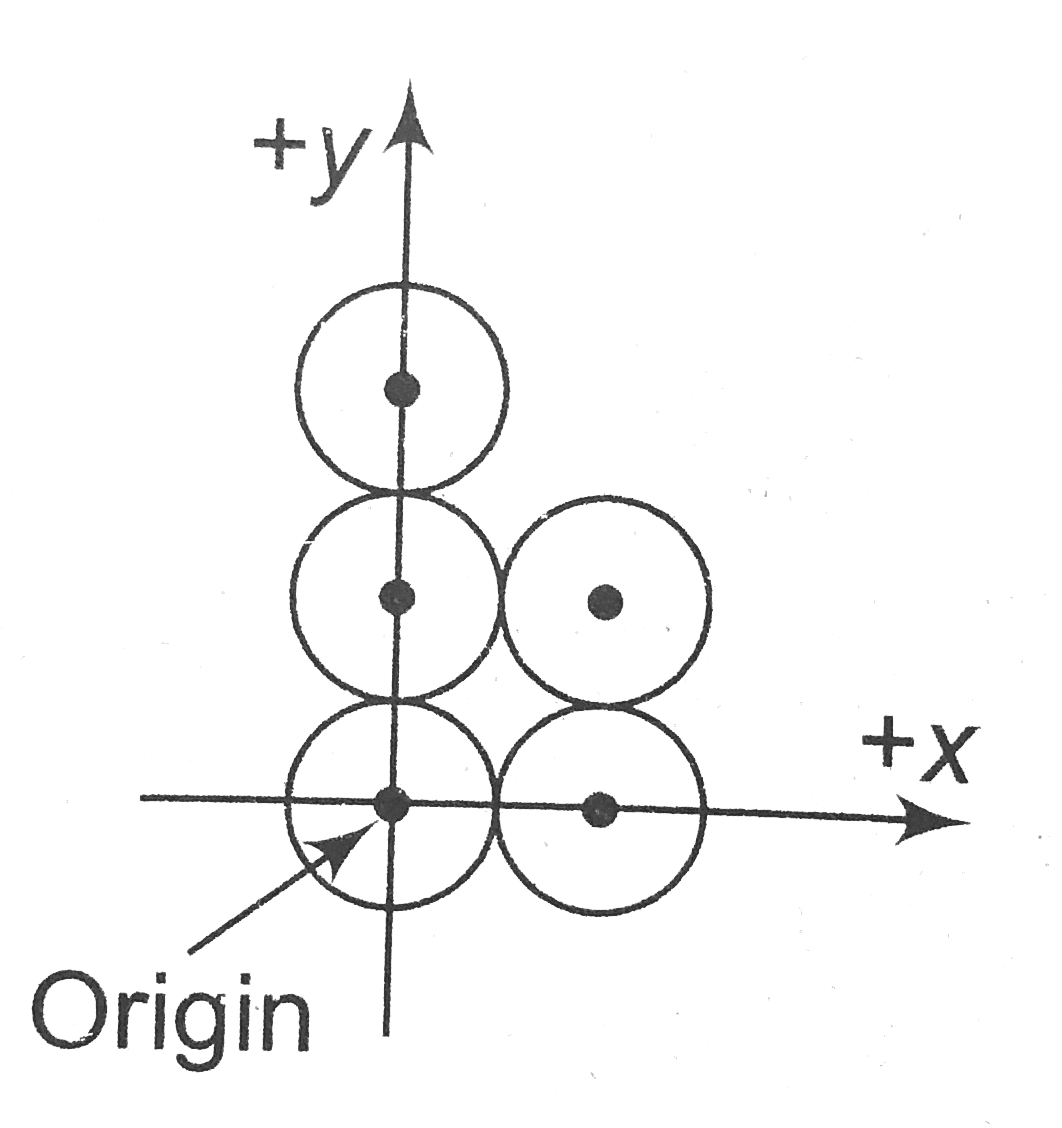 .
.
View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be
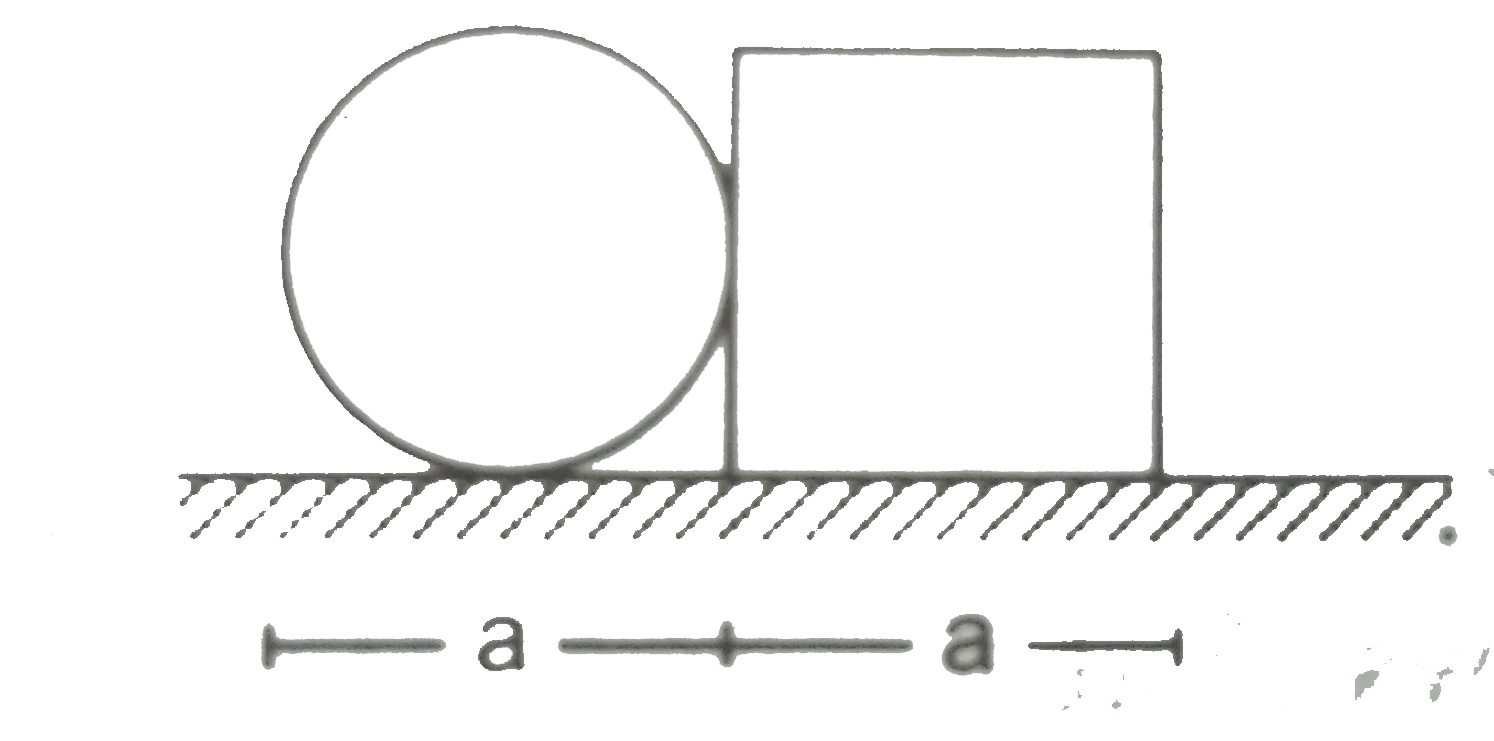 .
.
View SolutionA wire of uniform cross-section is bend in the shape shown in figure. The co-ordinate of the centre of mass of each side are shown in (figure). The co-ordinates of the centre of mass of the system are.
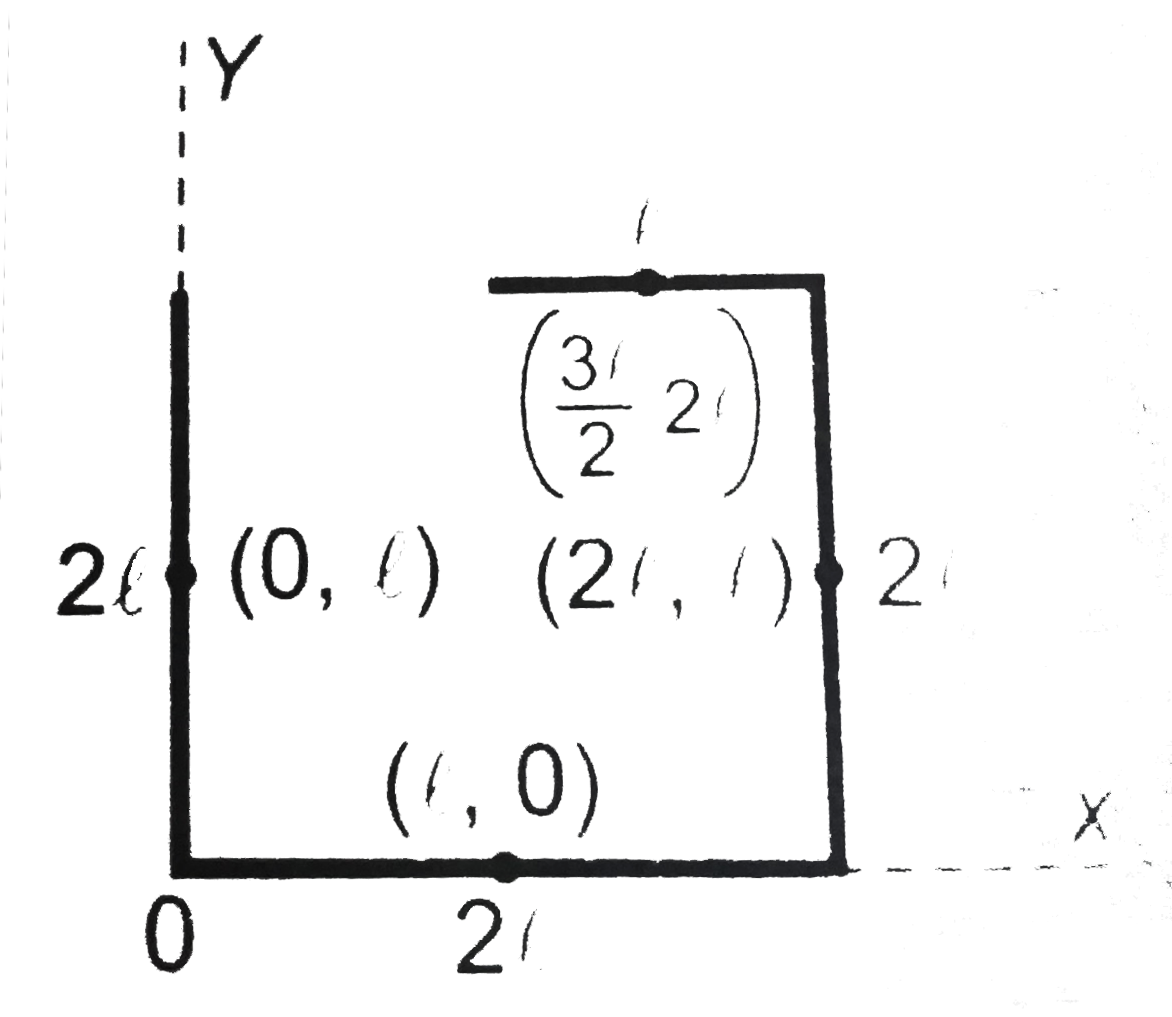 .
.
View SolutionA homogeneous plate
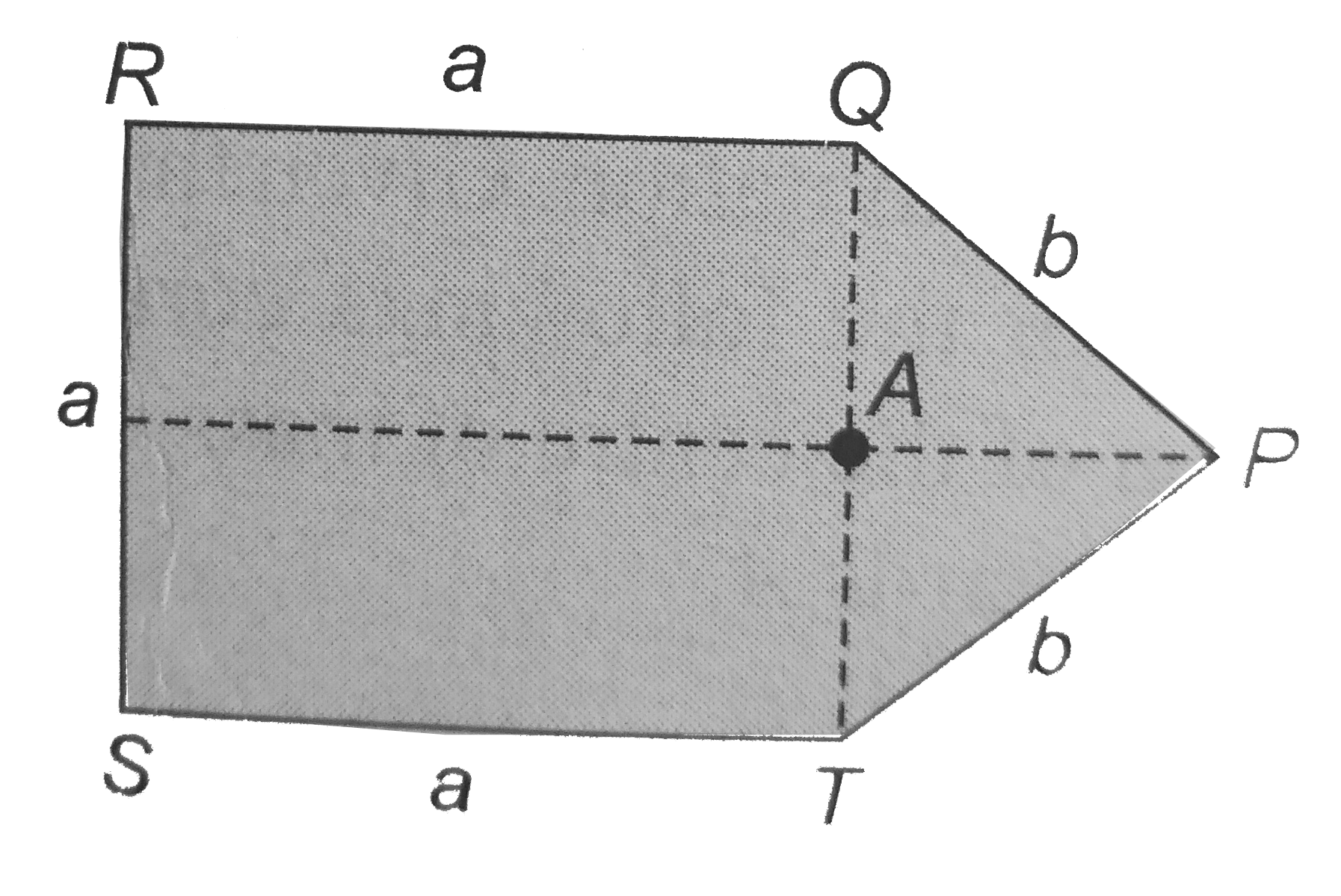 .
.
View SolutionEight solid uniform cubes of edge
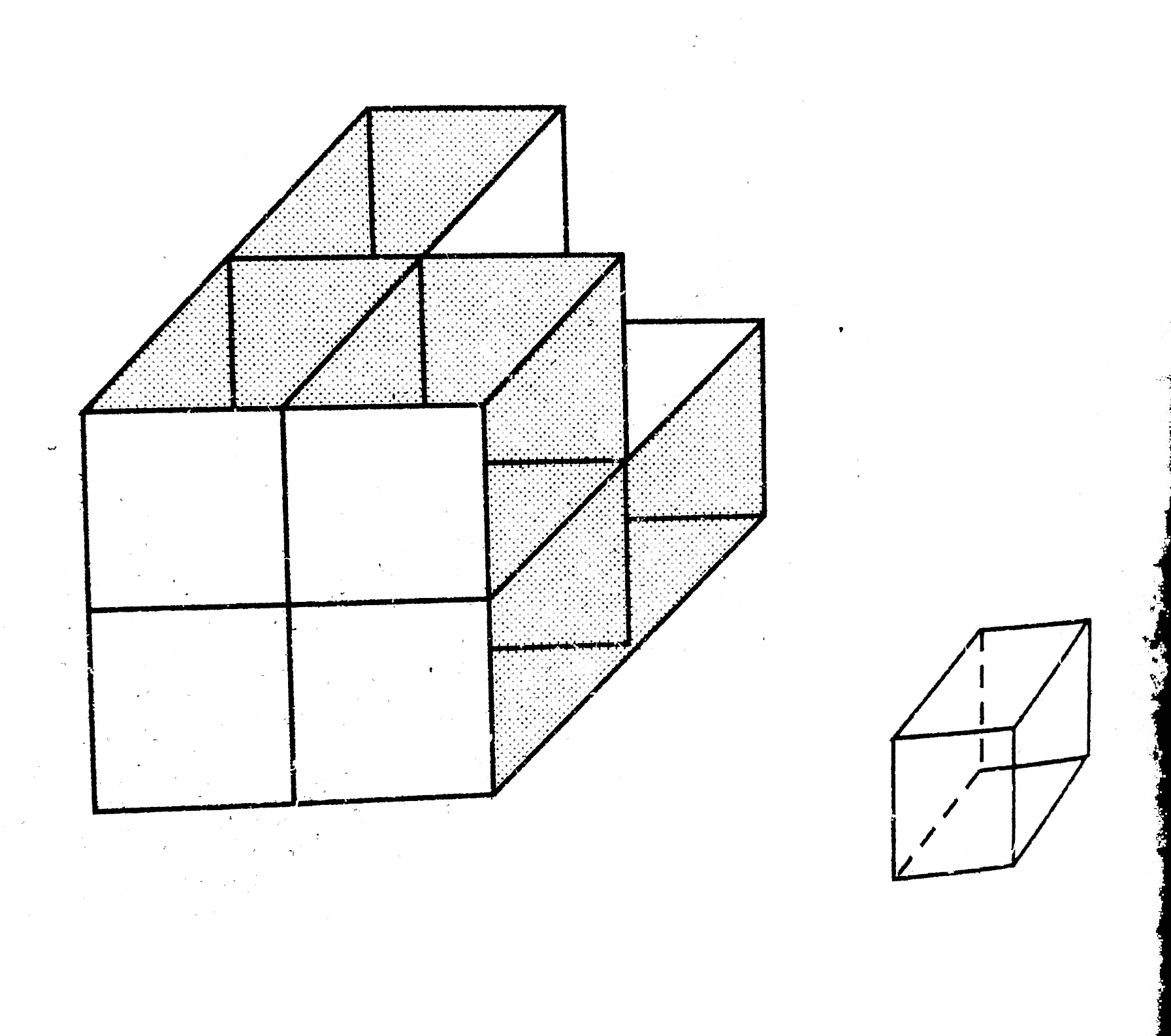 .
.
View SolutionFrom the circular disc of radius
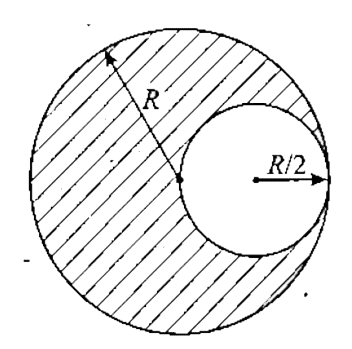
View SolutionA disc (of radius r cm) of uniform thickness and uniform density
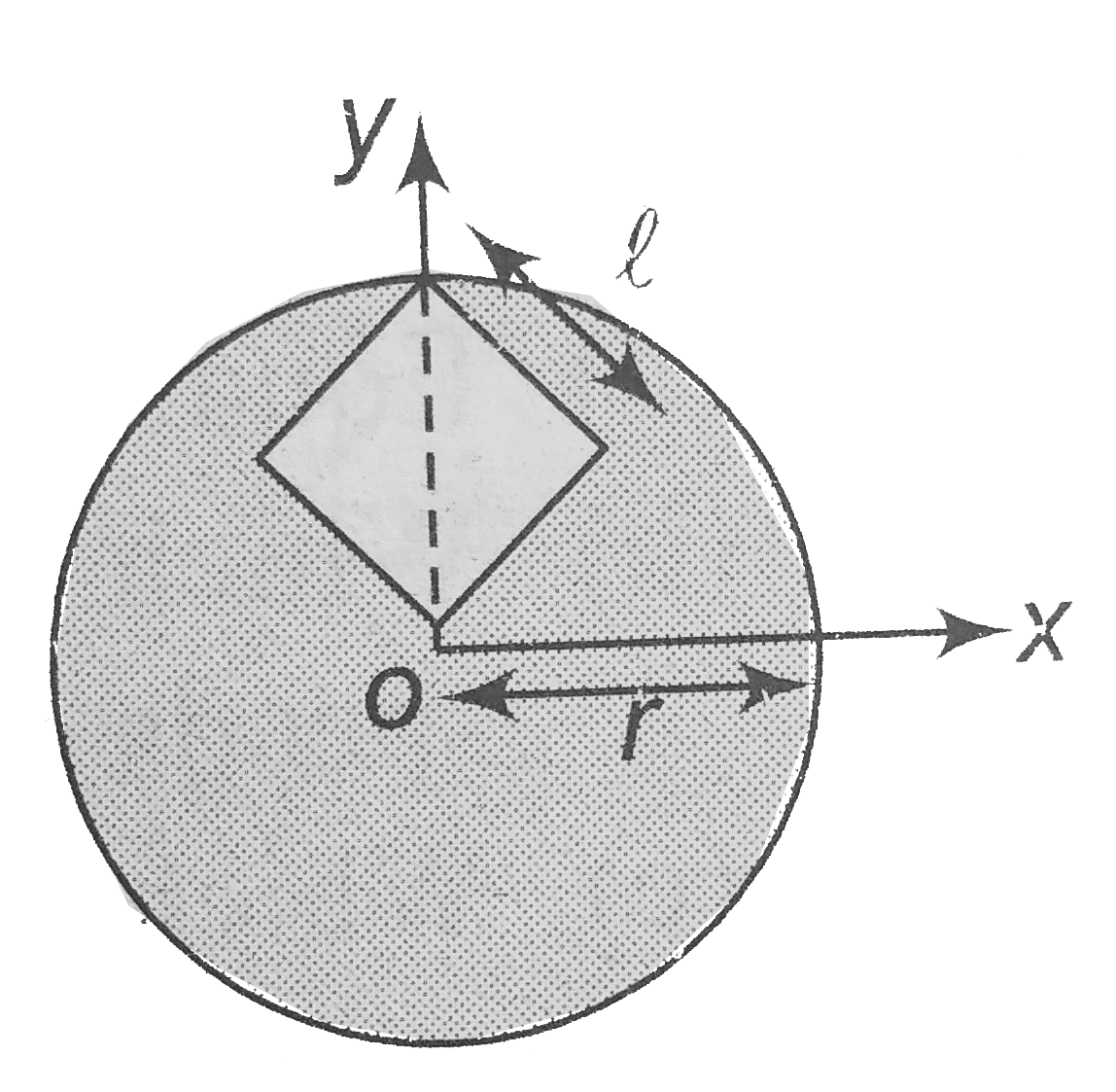 .
.
View SolutionFigure shown a cubical box that has been constructed from uniform metal plate of negligible thickness. The box is open at the top and has edge length
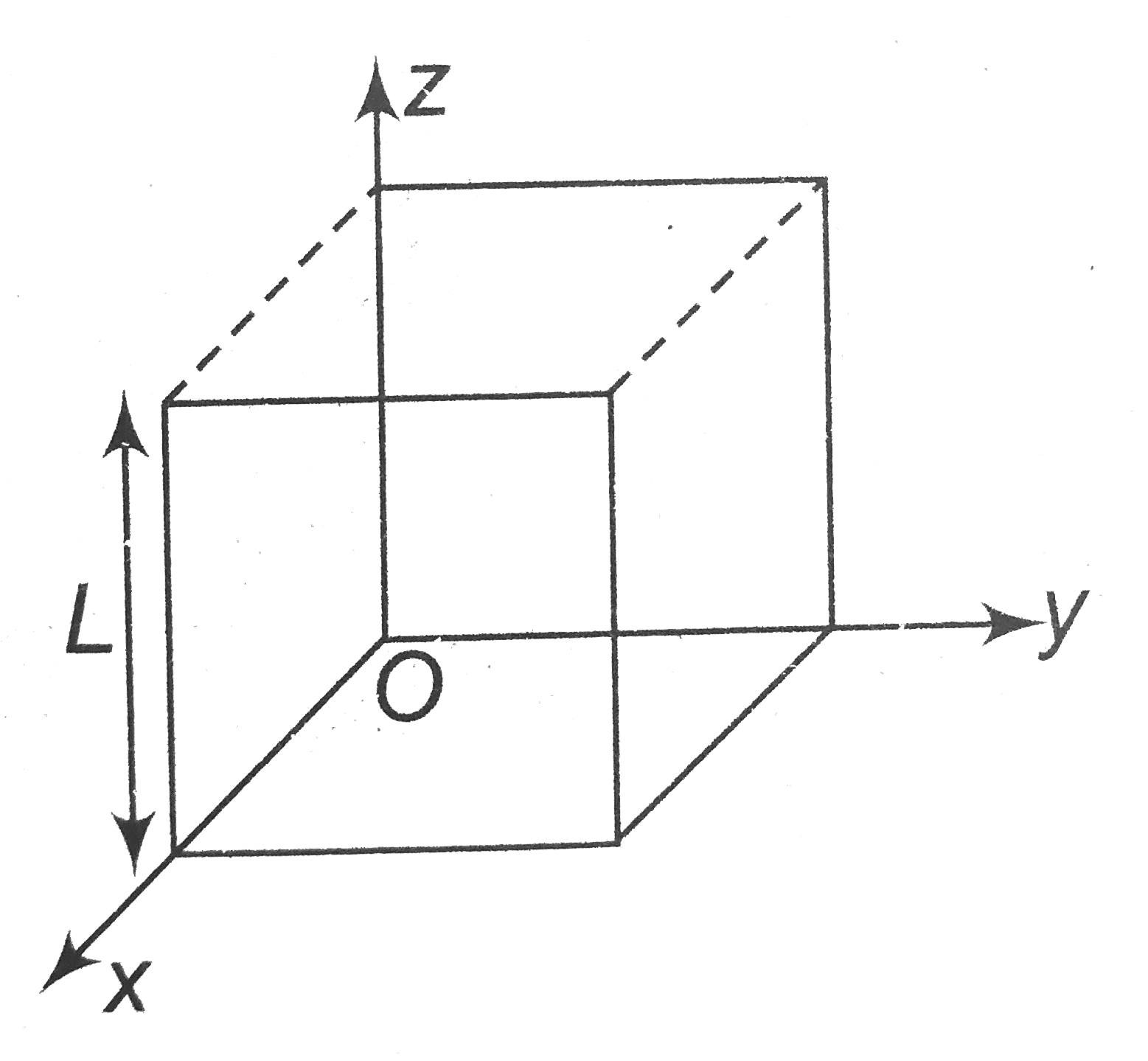 .
.
View SolutionThe centre of mass of a non uniform rod of length L, whose mass per unit length varies as
View Solution
Centre Of Mass questions and complete solutions for chapter ROTATIONAL DYNAMICS of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS ROTATIONAL DYNAMICS
- AIIMS Questions
- Angular Momentum And Its Conservation
- Assertion Reasoning
- Centre Of Mass
- Chapter Test
- Displacement , Velocity And Acceleration Of Centre Of Mass
- Moment Of Inertia
- NEET Questions
- Problems Based On Mixed Concepts
- Rotation And Translation Combined And Rolling Motion
- Rotational Kinematics
- Torque , Torque Equation And Equilibrium Of A Rigid Body
- Work And Energy In Case Of Rotation