Complete Solutions to Angular Momentum And Its Conservation of chapter ROTATIONAL DYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL DYNAMICS |
| A2Z | Angular Momentum And Its Conservation |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
A constant torque acting on a uniform circular wheel changes its angluar momentum from `A_0` to `4 A_0` in `4 s`. The magnitude of this torque is equal to.
View SolutionA mass M moving with a constant velocity parlale to the X-axis. Its angular momentum with respect to the origin
View SolutionA solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same which one of the following wil not be affected?
View SolutionA particle of mass `M` may move with the velocity `v`, along `AO`, or `DE` or `BC`. Then which of the following statements is not correct about particle's angular momentum about point `O`.
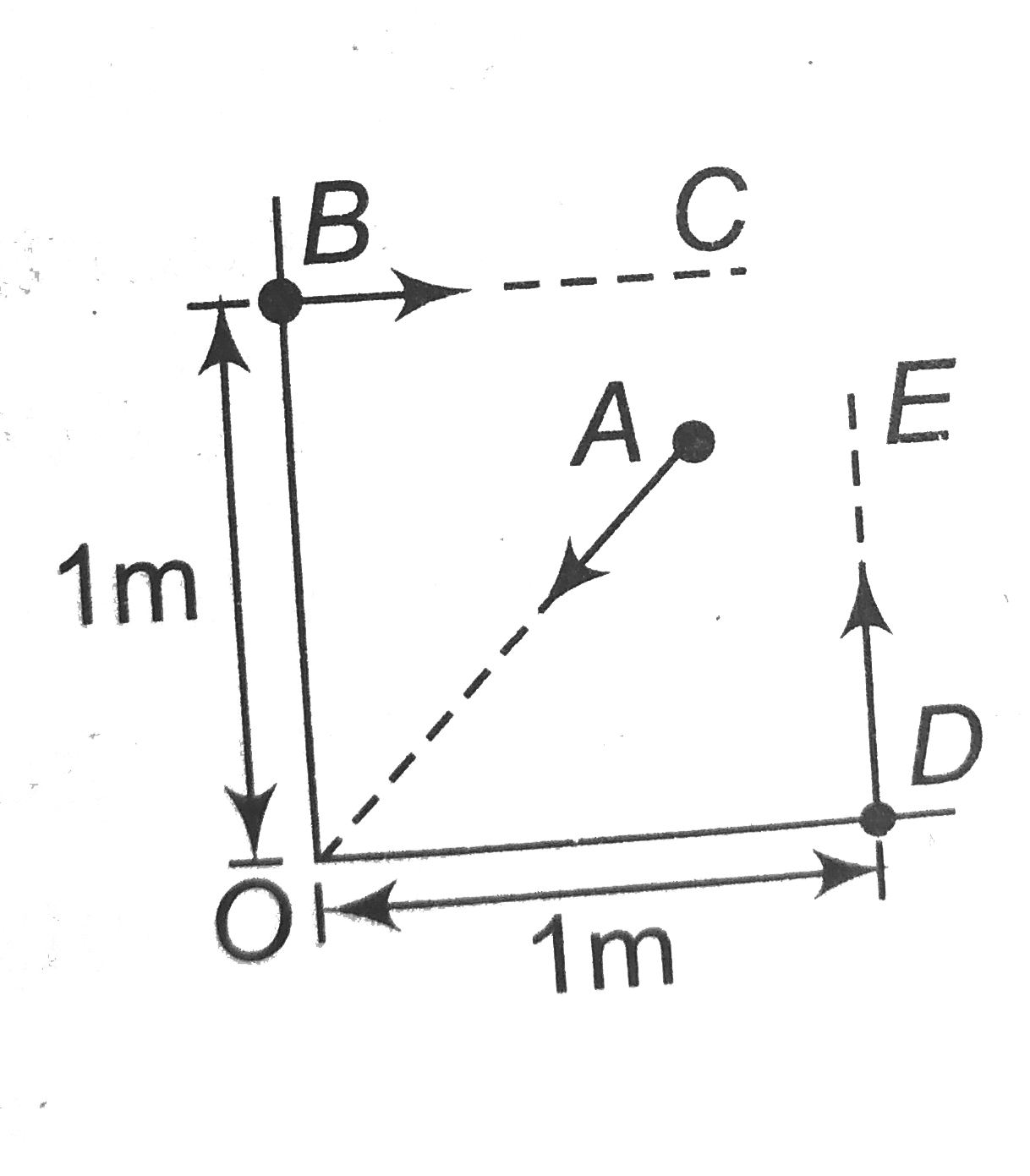 .
.
View SolutionA particle is made to move in circular path with decreasing speed. Which of the following is correct ?
View SolutionA body of mass `m` and radius `r` is released from rest along a smooth inclined plane of angle of inclination `theta`. The angular momentum of the body about the instantanoues point contact after a time `t` from the instant of release of equal is :
View SolutionConsider an isolated system moving through empty space. The system consists of objects that interact with each other and can change location with respect to one another. Which of the following quatities can change in time ?
View SolutionFor a particle of a mass `100 gm`, position and velocity at any instant are given as `10 hat i+ 6 hat j cm` and `vec v = 5 hat I cm//s`. Calculate the angular momentum about the point (1,1) cm.
View SolutionA particle of mass m moves in the xy-plane with velocity of `vec v = v_x hat i+ v_y hat j`. When its position vector is `vec r = x vec i + y vec j`, the angular momentum of the particle about the origin is.
View SolutionA hollow straight tube of length `l` and mass `m` can turn freely about its centre (fixed) on a smooth horizontal table. Another smooth uniform rod of same length and mass is fitted into the tube so that their centres coincide. They system is set in motion with an initial angular velocity `omega_0`. the angular velocity of the rod at an instant when the rod slips out of the tube is :
View SolutionA particle mass 1 kg is moving along a straight line `y=x+4`. Both x and y are in metres. Velocity of the particle is `2m//s`. Find the magnitude of angular momentum of the particle about origin.
View SolutionA circular platform is mounted on a vertical frictionless axle. Its radius is `r = 2 m` and its moment of inertia`I = 200 kg m^2`. It is initially at rest. A `70 kg` man stands on the edge of the platform and begins to walk along the edge at speed `v_0 = 1 m s^-1` relative to the ground. The angular velocity of the platform is.
View SolutionAn solid cylinder of mass `20 kg` and radius `20 cm` rotates about its axis with a angular speed `100 rad s^-1`. The angular momentum of the cylinder about its axis is.
View SolutionA child is standing with his two arms outstretched at the centre of a turntable that is rotating about its central axis with an angular speed `omega_0`. Now, the child folds his hands back so that moment of inertia becomes `3` times the initial value. The new angular speed is.
View SolutionTwo discs of moments of inertia `I_1` and `I_2` about their respective axes, rotating with angular frequencies, `omega_1` and `omega_2` respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be `A`.
View SolutionA ballet dancer, dancing on a smooth floor is spinning about a vertical axis with her arms folded with angular velocity of `20 rad//s`. When the stretches her arms fully, the spinning speed decrease in `10 rad//s`. If `I` is the initial moment of inertia of the dancer, the new moment of inertia is.
View SolutionA man stands on a rotating platform with his arms stretched holding a `5 kg` weight in each hand. The angular speed of the platform is `1.2 rev s^-1`. The moment of inertia of the man together with the platform may be taken to be constant and equal to `6 kg m^2`. If the man brings his arms close to his chest with the distance `n` each weight from the axis changing from `100 cm` to`20 cm`. The new angular speed of the platform is.
View SolutionA uniform solid disk of mass `m = 3.0 kg` and radius `r = 0.20 m` rotates about a fixed axis perpendicular to its face with angular frequency `0.6 rad/s`. The magnitude of the angular momentum of the disk when the axis of rotation momentum of the disk when the axis of rotation passes through a point midway between the centre and the rim is.
View SolutionA projectile of mass `m` is launched with an initial velocity `vec v_i` making an angle `theta` with the horizontal as shown in figure. The projectile momentum of the particle about the origin when it is at the highest point of its trajectory is.
 .
.
View SolutionIn previous problem, the angular momentum of the projectile about the origin when it just before hits the ground should be.
View SolutionA conical pendulum consists of a bob of mass `m` in motion in a circular path in a horizontal plane as shown in figure. During the motion, the supporting wire of length `l`. Maintains a constant angle `theta` with the vertical. The magnitude of the angular momentum of the bob about the vertical dashed line is.
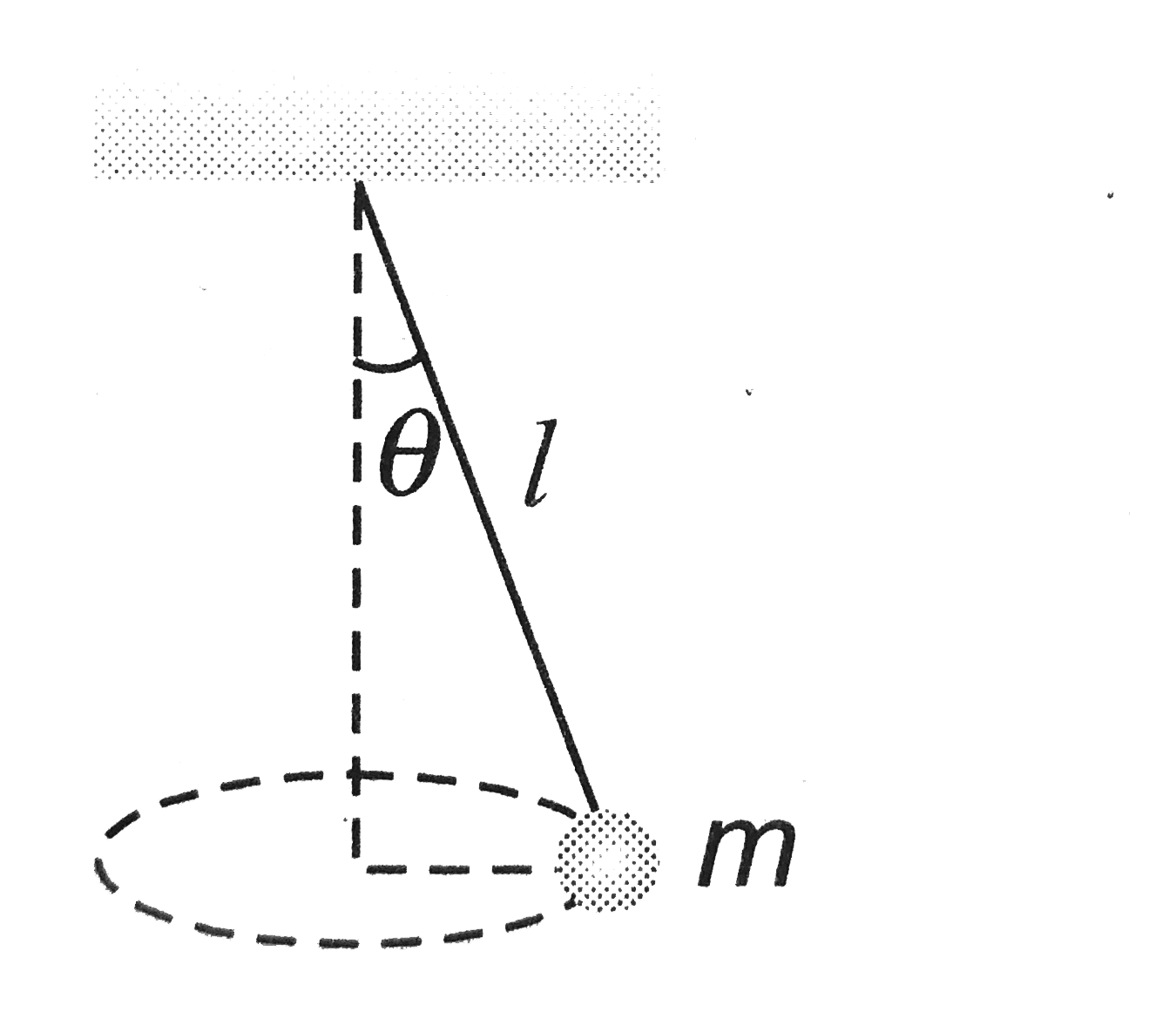 .
.
View SolutionA uniform solid sphere of radius `r = 0.500 m` and mass `m = 15.0 kg` turns counterclockwise about a vertical axis through its centre.Find its vector angular momentum about this axis when its angular speed is `3.00 rad//s`.
View SolutionA disk with moment of inertia `I_1` rotates about frictionless, vertical axle with angular speed `omega_i` A second disk, this one having moment of inertia `I_2` and initial not rotating, drops onto the first disk (Fig.) Because of friction between the surfaces, the two eventually reach the same angular speed `omega_f`. The value of `omega_f` is.
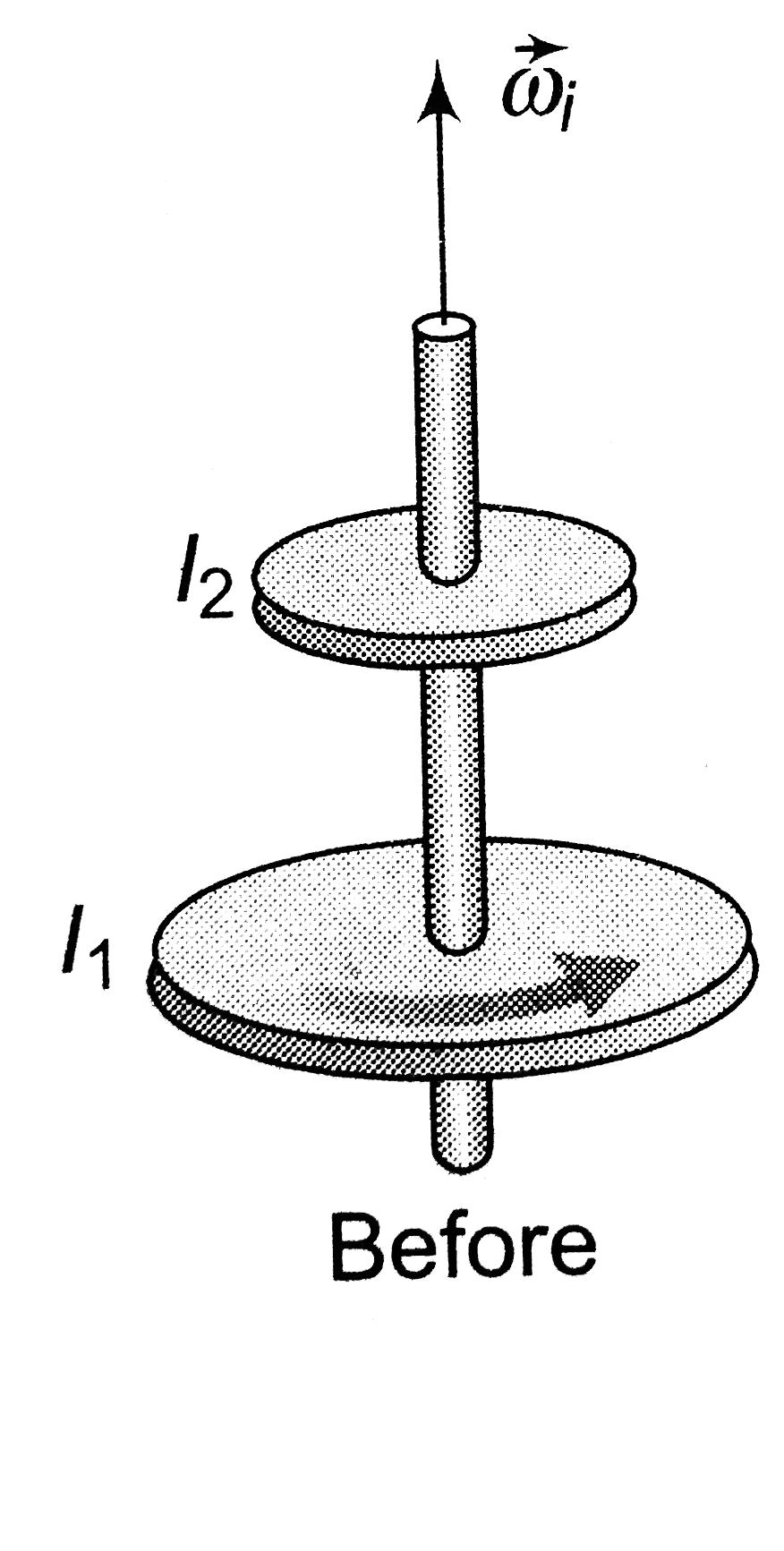 .
.
View SolutionA playground merry-go-round of radius `R = 2.00` has a moment of inertia `I = 250 kg.m^2` and is rotating `10.0 rev//min` about a frictionless, vertical axle. Facing axle, a `25.0-kg` child hops onto the merry-go-round and manages to sit down on the edge. The new angular speed of the merry-go-round is.
View SolutionA `60.0-kg` woman stands at the western rim of a horizontal turntable having a moment of inertia of `50 kg.m^2` and radius of `2.0 m`. The turntable is initially at rest and free to rotate abot a frictionless, vertical axle through its centre. The woman then starts walking around the rim clockwise` ("as viewed from above the system")` at constant speed of `1.50 m//s` relative to the Earth. The final angular velocity of the woman and the turntable systems.
View SolutionA student sits on a freely rotating stool holding dumbbells, each of mass `5.0 kg` (Fig). When his arms are extended horizontally (Fig a), the dumbbells are `1.0 m` from the axis of rotation and the student rotate with an angular speed of `1.0 rad//s`. The moment of inertia of the student plus stool is `5.0 kg.m^2` and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position `0.50 m` from the rotationa are (Fig.) The new angular speed of the student is.
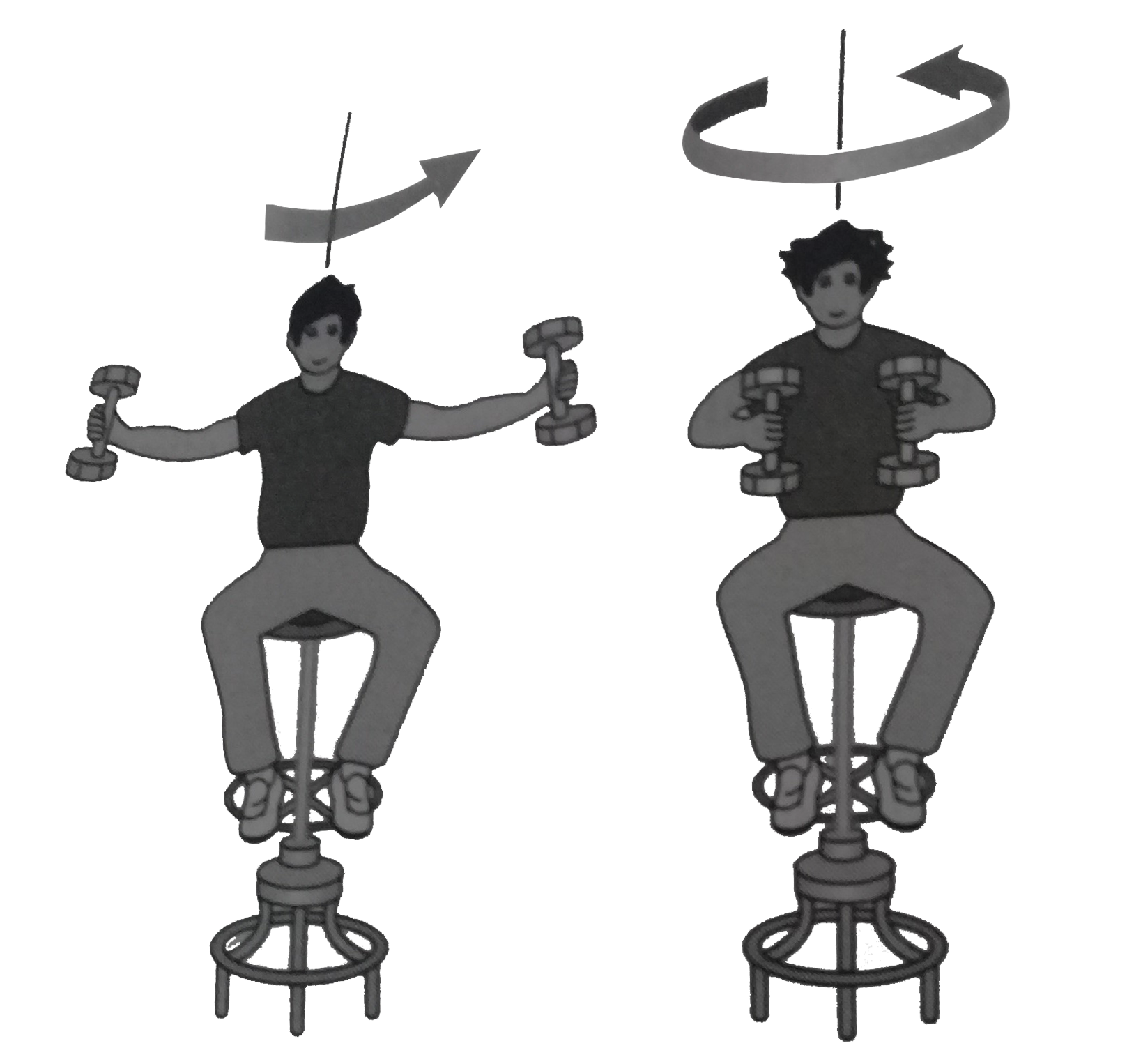 .
.
View SolutionA puck of mass `m = 50.0 g` is attached to a taut cord passing through a small hole in a frictionless, horizontal surface (Fig.) The puck is initially orbiting with speed `v_i = 1.50 m//s` in a circle of radius `r_i = 0.30 m`. The cord is then slowly pulled from below, decreasing the radius of the circle to `r = 0.10 m`. The puck's speed at the smaller radius is.
 .
.
View SolutionA horizontal platform in the shape of a circular disk rotates on a frictionless bearing about a vertical axle through the centre of the disk. The platform has a mass of `150 kg`, a radius of `2.0 m`, and a rotational inertia of`300 kg m^2` about the axis of rotation. A `60 kg` student walks slowly from the rim of the platform toward the centre. If the angular speed of the system is `1.5 rad//s` when the student starts at the rim, what is the angular speed when she is `0.50 m` from the centre ?
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View SolutionA girl of mass `M` stands on the rim of a frictionless merry-go-round of radius `R` and rotational inertia `I` that is not moving. She throws a rock of mass `m` horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the rock. relative to the ground, is `v`. After, the linear speed of the girl is.
 .
.
View Solution
Angular Momentum And Its Conservation questions and complete solutions for chapter ROTATIONAL DYNAMICS of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS ROTATIONAL DYNAMICS
- AIIMS Questions
- Angular Momentum And Its Conservation
- Assertion Reasoning
- Centre Of Mass
- Chapter Test
- Displacement , Velocity And Acceleration Of Centre Of Mass
- Moment Of Inertia
- NEET Questions
- Problems Based On Mixed Concepts
- Rotation And Translation Combined And Rolling Motion
- Rotational Kinematics
- Torque , Torque Equation And Equilibrium Of A Rigid Body
- Work And Energy In Case Of Rotation