Complete Solutions to Problems Based On Mixed Concepts of chapter ROTATIONAL DYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL DYNAMICS |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
A uniform rod of mass `m` and length `l_(0)` is rotating with a constant angular speed `omega` about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle `theta` to the vertical (axis of rotation).
View SolutionTwo points `A` and `B` on a disc have velocities `v_1` and `v_2`, respectively, at some moment. Their directions make angles `60^@` and `30^@` respectively, with the line of separation as shown in figure. The angular velocity of disc is :
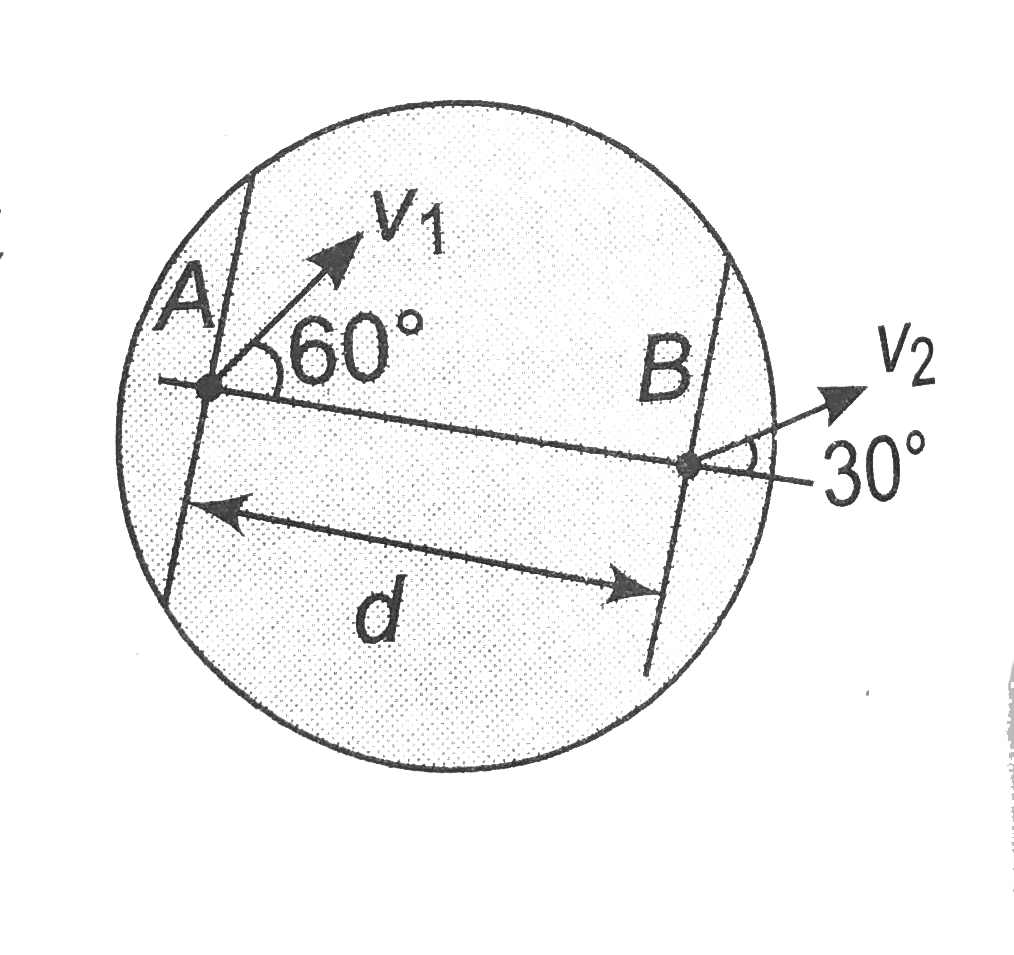 .
.
View SolutionTwo steel ball of equal diameter are connected by a rigid bar of negligible weight as shown and are dropped in the horizontal position from height `h` above the heavy steel and brass base plates. If the coefficient of restitition between the ball and steel base is `0.6` and the between the other ball and the brass base is `0.4`. The angular velocity of the bar immediately after rebound is. (Assume the two impacts are simultaneous).
 .
.
View SolutionA brick of length `L` is placed on the horizontal floor. The bricks of same length and size are placed on this brick, one above the other by providing a margin of `(L)/(8)` from the edge of the brick placed just below, in the same direction.
Find the correct option.
View SolutionA car moves with speed `v` on a horizontal circular track of radius `R`. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is `h`, and the separation between its inner and outer wheels is `d` The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .
.
View SolutionA thin horizontal uniform rod `AB` of mass `m` and length `l` can rotate freely about a vertical axis passing through its end `A`. At a certain moment, the end `B` starts experiencing a constant force `F` which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle `theta` measured relative to the initial position should be.
View SolutionA uniform disc of mass `m` is fitted (pivoted smoothly) with a rod of mass `m//2`. If the bottom of the rod os pulled with a velocity `v`, it moves without changing its and of orientation and the disc rolls without sliding. Take kinetic energy of the system (rod + disc) is.
 .
.
View SolutionThe two uniform discs rotate separately on parallel axles. The upper disc (radius `a` and momentum of inertia `I_1`) is given an angular velocity `omega_0` and the lower disc of (radius `b` and momentum of inertia `I_2`) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
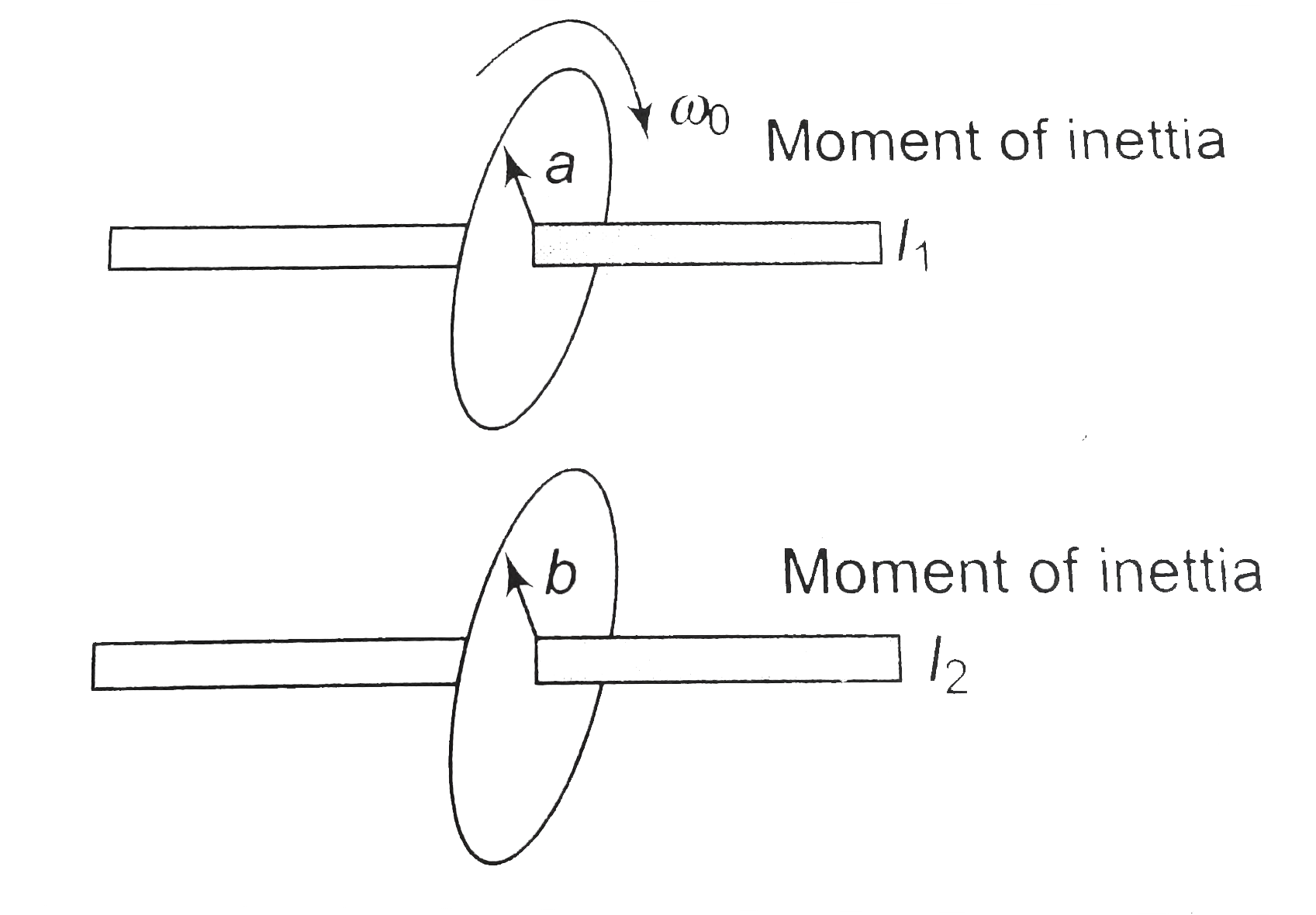 .
.
View SolutionA sphere of mass `M` and radius `r` shown in figure slips on a rough horizontal plane. At some instant it has translational velocity `V_(0)` and rotational velocity about the centre `(v_(0))/(2r)`. Find the translational velocity after the sphere starts pure rolling.
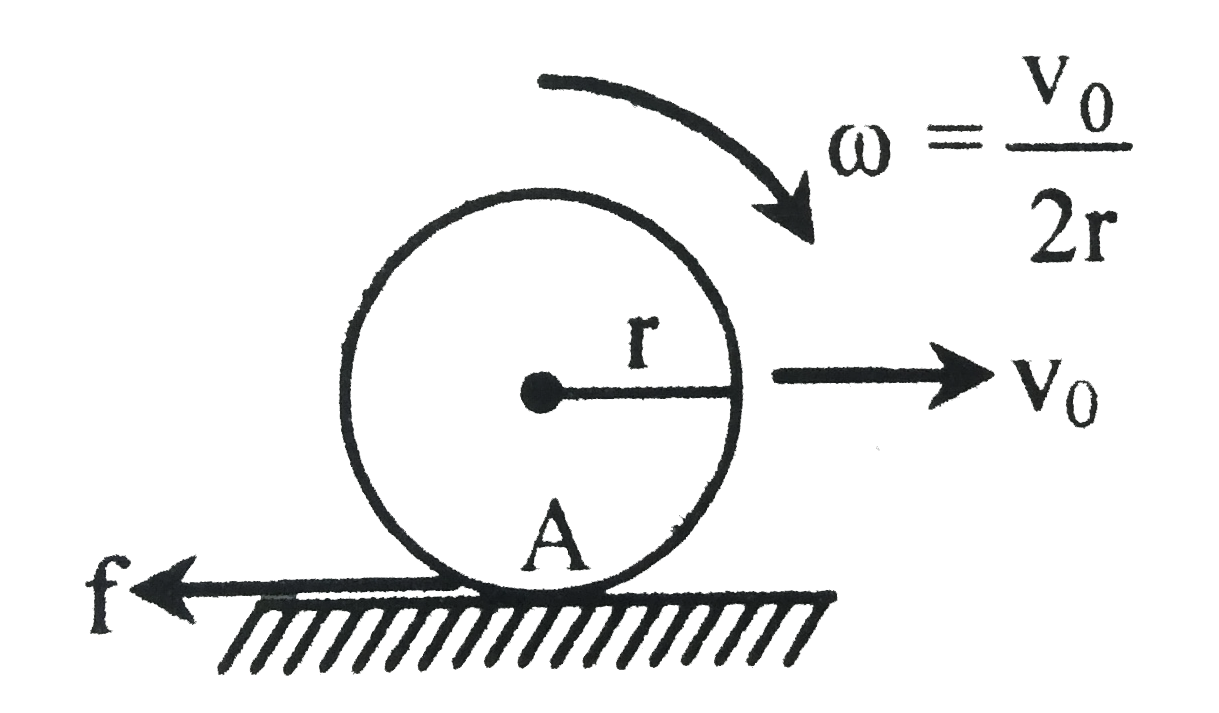 .
.
View SolutionA wheel of mass `5 kg` and radius `0.40 m` is rolling on a road without sliding with angular velocity `10 rad s^-1`. The moment of ineria of the wheel about the axis of rotation is `0.65 kg m^2`. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
View SolutionThe moments of inertia of two rotating bodies `A` and are `I_A` and `I_B(I_A gt I_B)`. If their angular momenta are equal then.
View SolutionA body is rolling down an inclined plane. If kinetic energy of rotation is `40 %` of kinetic energy in translatory state then the body is a
View SolutionA ring of radius `R` is rotating with an angular speed `omega_0` about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is `mu_k`. The time after it starts rolling is.
View SolutionA uniform solid sphere of radius `r = ( R)/(5)` is placed on the inside surface of a hemisherical bowl with radius `R (= 5 r)`. The sphere is released from rest at an angle `theta = 37^@` to the vertical and rolls without slipping (Fig.) The angular speed of the sphere when it reaches the bottom of the bowl is.
 .
.
View SolutionAverage torque on a projectile of mass `m` (initial speed `u` and angle of projection `theta`) between initial and final positions `P` and `Q` as shown in figure, about the point of projection is :
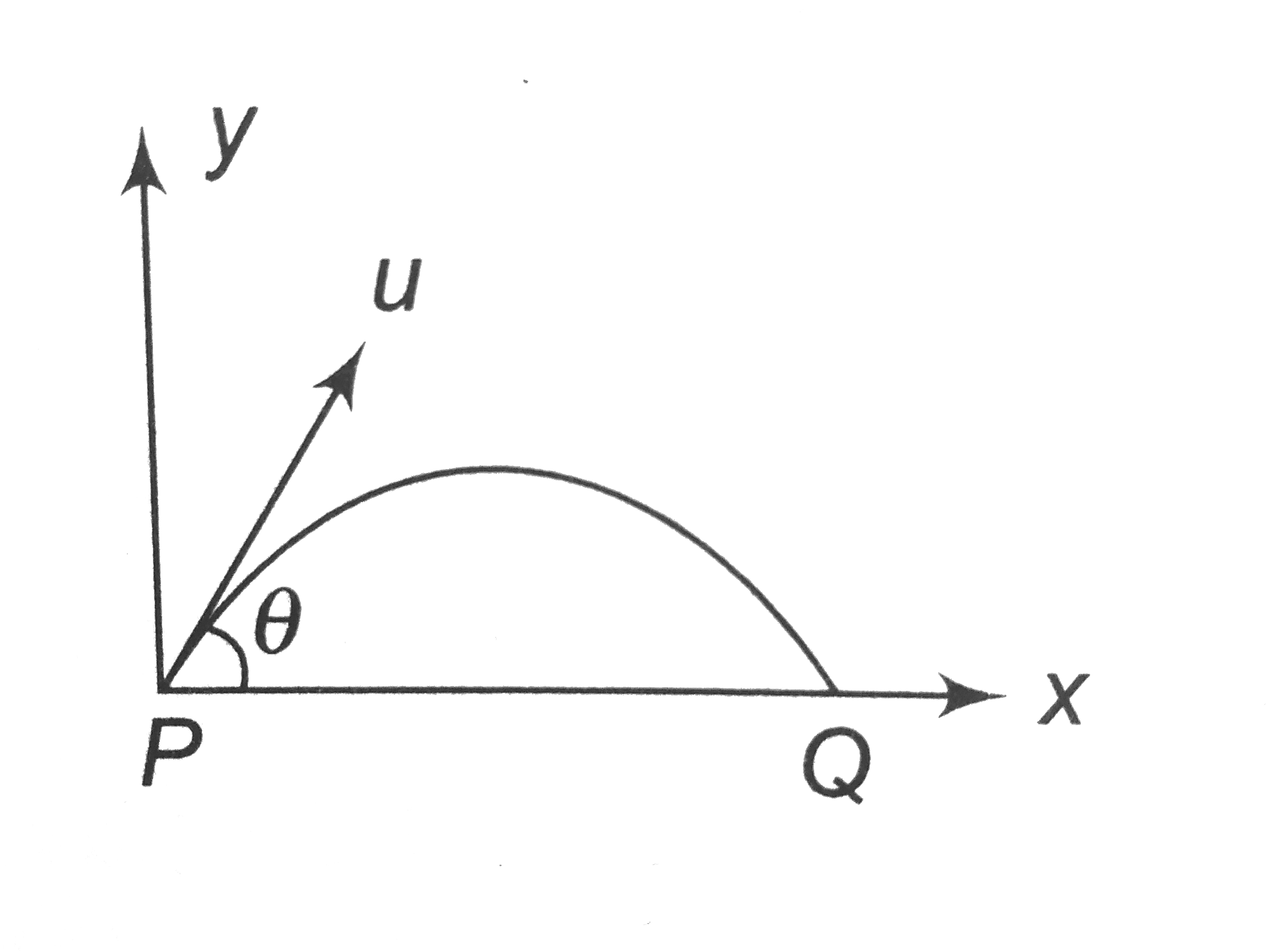 .
.
View SolutionA car weighs `1800 kg`. The distance between its front and back axles is `1.8 m`. Its centre of gravity is `1.05 m` behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
View SolutionA track is mounted on a large wheel that is free to turn with neigligible friction about a vertical axis (Fig). A toy train of mass `M` is placed on the track and, with the system initially at rest, the train's electrical power is turned on. The train reaches speed `v` with respect to the track. What is the wheel's angular speed if its mass is `m` and its radius is `r` ? (Treat it as a hoop, and neglect the mass of the spokes and hub).
 .
.
View SolutionA sphere of mass `M` rolls without slipping on rough surface with centre of mass has constant speed `v_0`. If mass of the sphere is `m` and its radius be R`, then the angular momentum of the sphere about the point of contact is.
View SolutionFigure shows two identical particles `1` and `2`, each of mass `m`, moving in opposite directions with same speed `vec V` along parallel lines. At a particular instant, `vec r_1` and `vec r_2` are their respective position vectors drawn from point `A` which is in the plane of the parallel lines. Which of the following is the correct statement ?
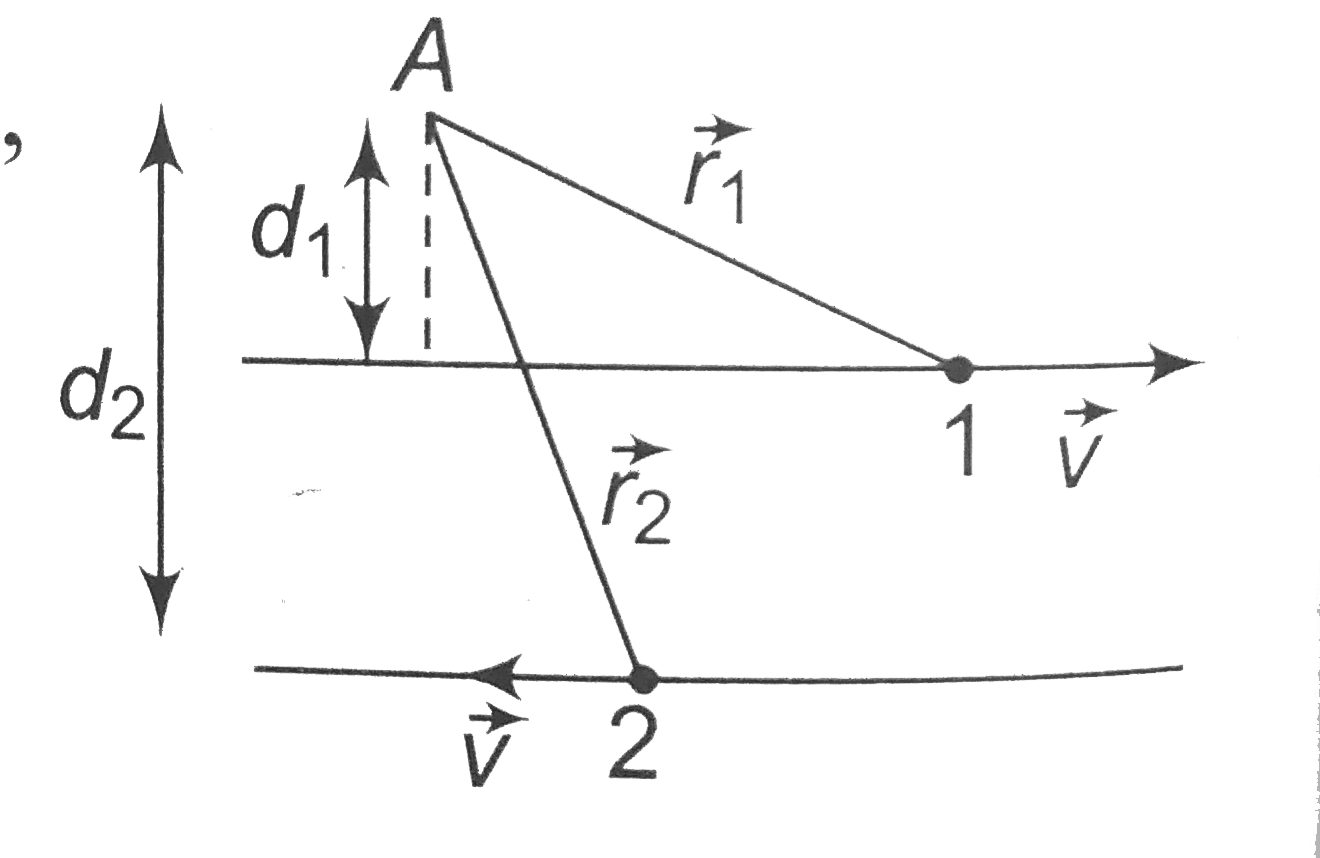 .
.
View SolutionA cylindrical rod of mass `M`, length `L` and radius `R` has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
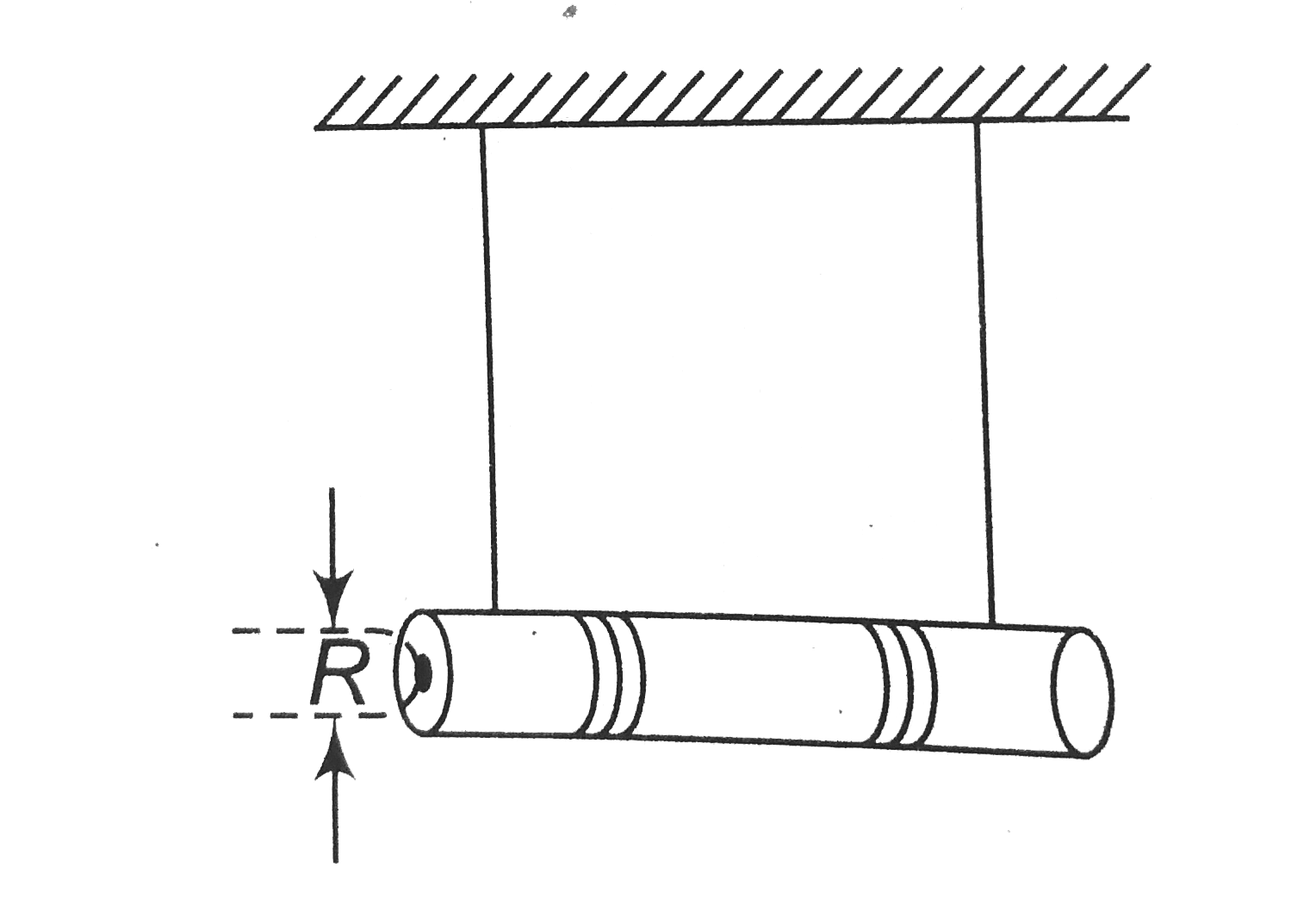 .
.
View SolutionThe moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is `1 kg-m^2`. It is rotating with an angular velocity `100 radia//sec`. Another indentical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilojoules is :
View SolutionA vertical disc of mass `5 kg` and radius `50 cm` rests against a steo of height `25 cm` as shown in figure. What minimum horizontal force applied perpendicular to the axle will make the disc to climb the step ? Take `g = 10 m//s^2`.
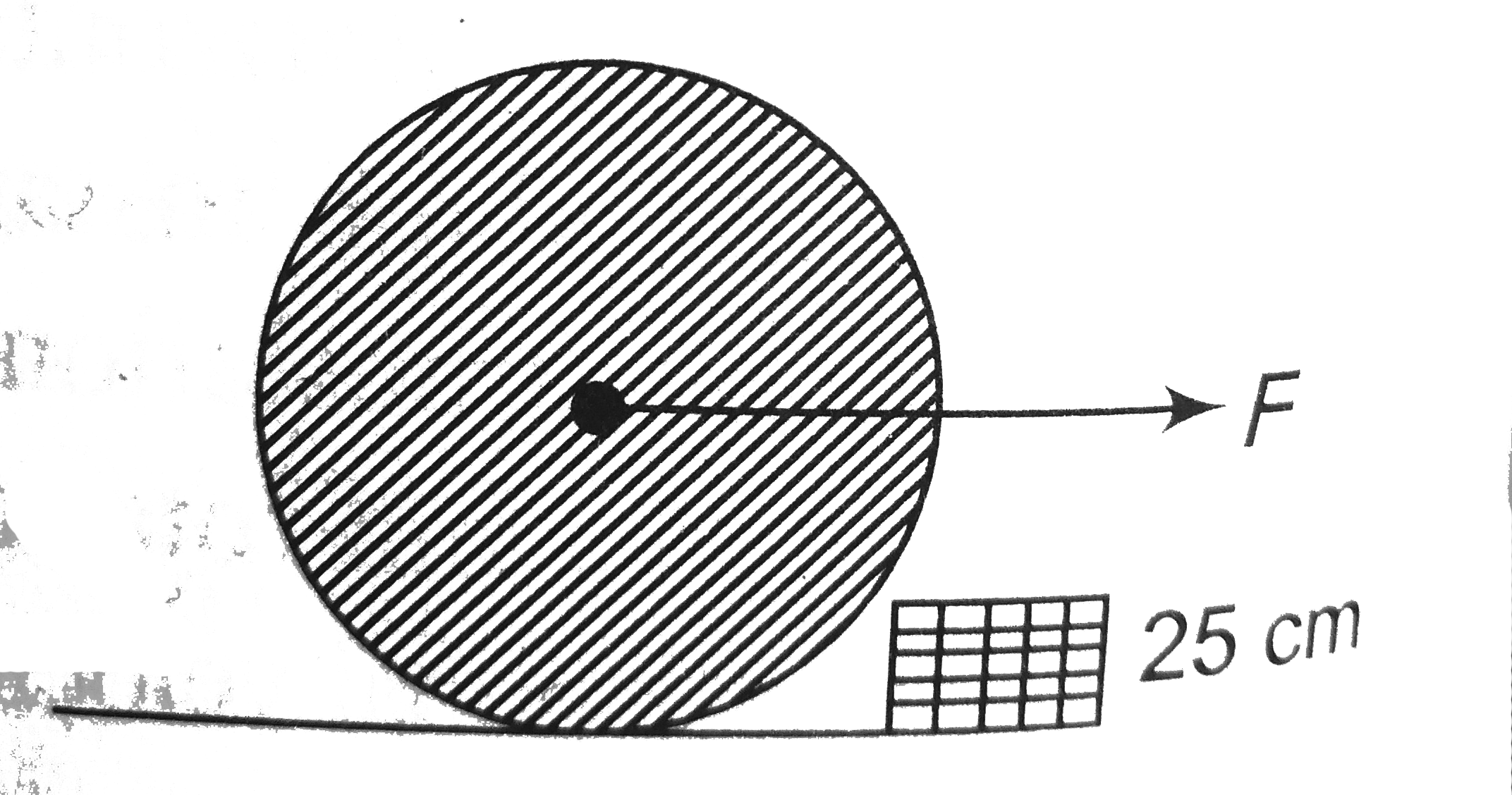 .
.
View SolutionThe rope shown in figure is wound around a cylinder of mass `4 kg` and moment of inertia `0.02 kgm^2` about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
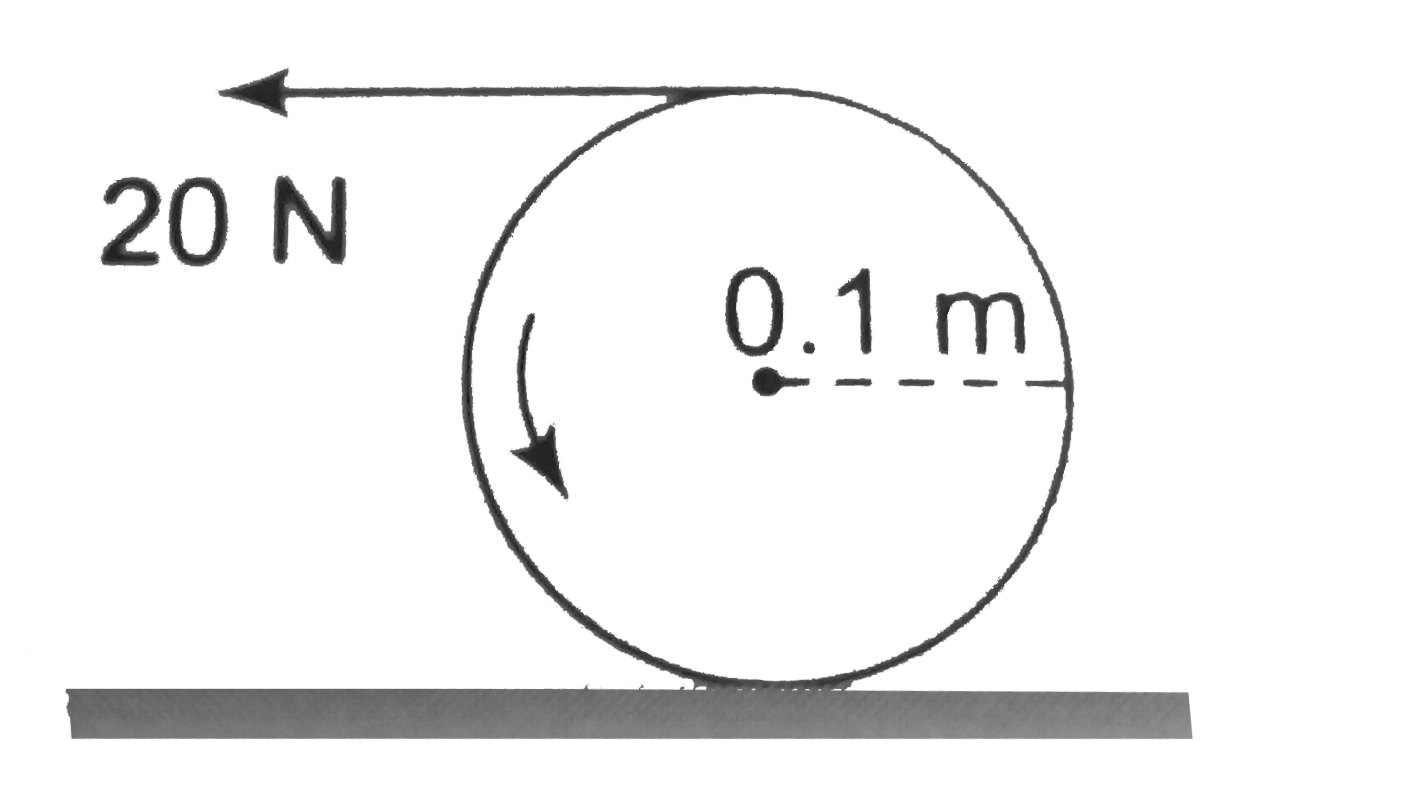 .
.
View SolutionA small sphere `D` of mass and radius rols without slipping inside a large fixed hemispherical radius `R( gt gt r)` as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom `B` of the hemisphere.
 .
.
View SolutionFigure shows a rough track a portion of which is in the form of a cylinder of radius `R`. With what minimum linear speed should as sphere of radius `r` be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed of the block after it hits O is
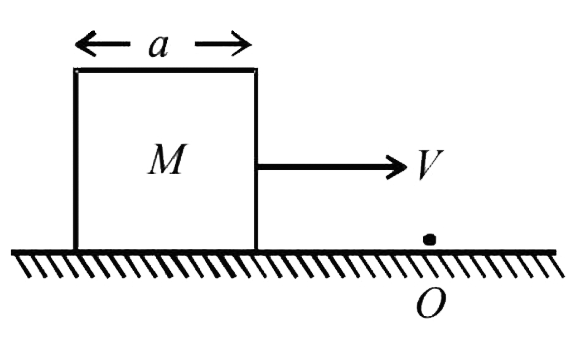
View SolutionA body A of mass M while falling wertically downwards under gravity brakes into two parts, a body B of mass `(1)/(3)` M and a body C of mass `(2)/(3)` M. The center of mass of bodies B and C taken together shifts compared to that of body A towards
View SolutionMasses of `2 kg` each are placed at the corners `B` and `A` of a rectangular plate `ABCD` as shown in the figure. A mass of `8 kg` has to be placed on the plate so that the centre of mass of the system should be the centre `O`. Then the mass should be placed at :
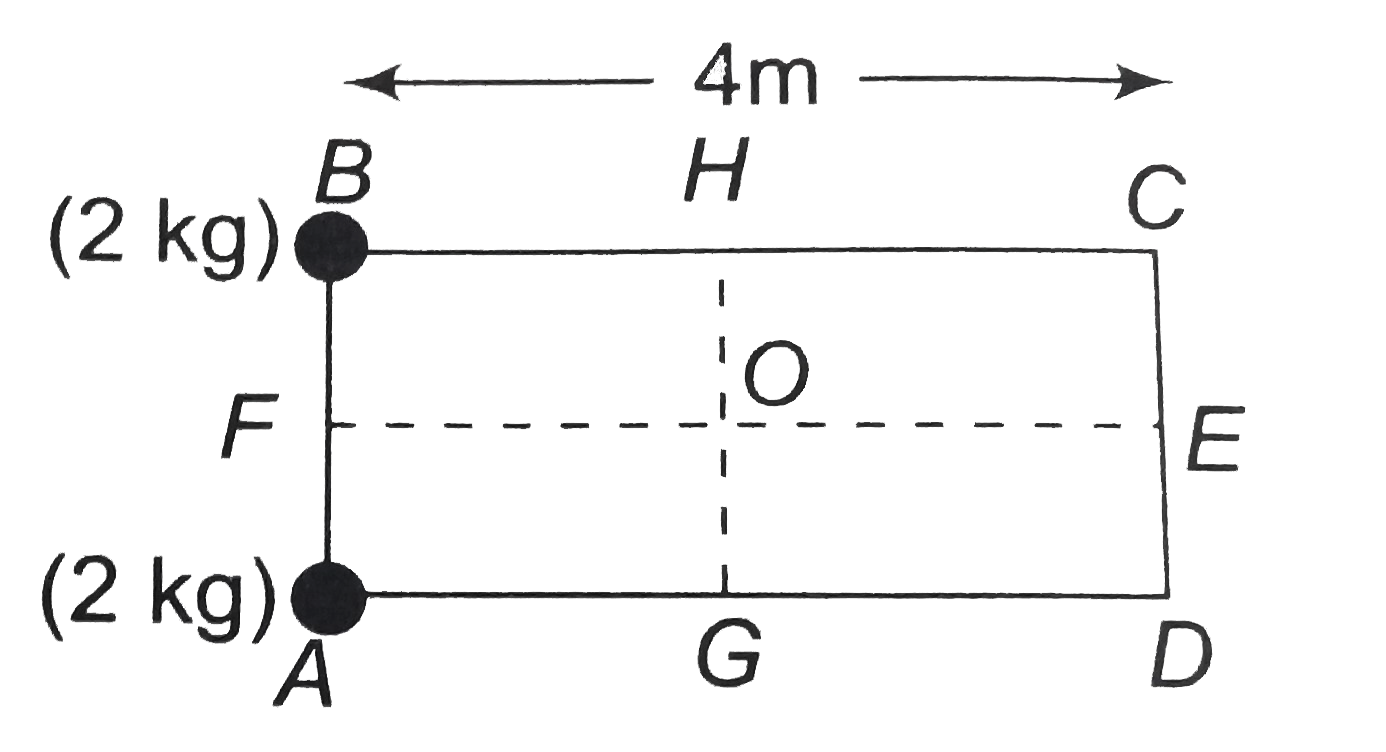 .
.
View SolutionParticle of masses `m, 2m,3m,…,nm` grams are placed on the same line at distance `l,2l,3l,…..,nl cm` from a fixed point. The distance of centre of mass of the particles from the fixed point in centimeters is :
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionA uniform cylinder has radius `R` and length `L`. If the moment of inertia of this cylinder about an axis passing through its centre and normal to its circular face is `(mR^(2))/2` is equal to moment of inertia of the same cylinder about an axis passing through its centre and normal to its length, then
View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter ROTATIONAL DYNAMICS of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS ROTATIONAL DYNAMICS
- AIIMS Questions
- Angular Momentum And Its Conservation
- Assertion Reasoning
- Centre Of Mass
- Chapter Test
- Displacement , Velocity And Acceleration Of Centre Of Mass
- Moment Of Inertia
- NEET Questions
- Problems Based On Mixed Concepts
- Rotation And Translation Combined And Rolling Motion
- Rotational Kinematics
- Torque , Torque Equation And Equilibrium Of A Rigid Body
- Work And Energy In Case Of Rotation