Complete Solutions to Equation Of Shm , Phase And Comparing Shm With Uniform Circular Motion of chapter OSCILLATION AND SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATION AND SIMPLE HARMONIC MOTION |
| A2Z | Equation Of Shm , Phase And Comparing Shm With Uniform Circular Motion |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
A boby is moving in a room with a velocity of `20m//s` perpendicular to the two walls separated by 5 meters .There is no friction and the collision with the walls are elastic.
01:42View SolutionWhich of the following expression does not represent SHM?
01:58View SolutionThe function `sin^(2)(omega t)` represents:
02:49View SolutionThe displacement of a particle is represented by the equation `y = sin^(2) omega t` the motion is
04:36View SolutionA particle is performing SHM. if its displacement from mean position is `x`, a corresponding resultant force on y is `F` and acceleration is a, which of the following graph is correct?
02:10View SolutionThe equation of motion of a particle executing simple harmonic motion is `a+16pi^(2)x = 0` In this equation, a is the linear acceleration in `m//s^(2)` of the particle at a displacement x in meter. The time period in simple harmonic motion is
01:11View SolutionAt `t = 0` aparticle of mass `m` start moving from rest due to a force `vecF = F_(0) sin (omega t)hati` :
02:49View SolutionValues of the acceleration `A` of a particle moving in simple harmonic motion as a function of its displacement `x` are given in the table below.
`|{:(A(mm s^(-2)),16,8,0,-8,-16),(x(mm),-4,-2,0,2,4):}|`
The pariod of the motion is01:38View SolutionA particle executes simple harmonic motion between `x = -A and x = + A`. The time taken for it to go from 0 to` A//2` is ` T_1` and to go from` A//2` to `A` is `T_2`. Then.
02:52View SolutionThe time taken by a particle performing `SHM` on a straight line to pass from point `A` to `B` where its velocities are same is `2` seconds .After another `2` seconds it return to `B` The time period of oscillation is (in seconds)
01:59View SolutionA particle is perfroming simple harmoic motion along ` x-"axis"` with amplitude 4 cm and time period `1.2 sec`.The minimum time taken by the particle to move from x=2 cm to `x= + 4 cm` and back again is given by
04:55View SolutionTwo particles `P` and `Q` describe `S.H.M.` of same amplitude a, same frequency `f` along the same straight line from the same mean position. The maximum distance between the two particles is a `sqrt(2)`, If the initial phase difference between the particles is `(pi)/(N)` then find `N` :
03:53View SolutionA particle is executing `S.H.M.` of amplitude `4 cm` and `T = 4` sec. The time taken by it to move from positive extreme position to half the amplitude is
02:30View SolutionTwo particle undergoes `SHM` along parallel line with the same time period `(T)` and equal amplitude At a particular instant , one particle is at its extereme position while the other is at its mean position .They move in the same direction .They will cross each other after a further time
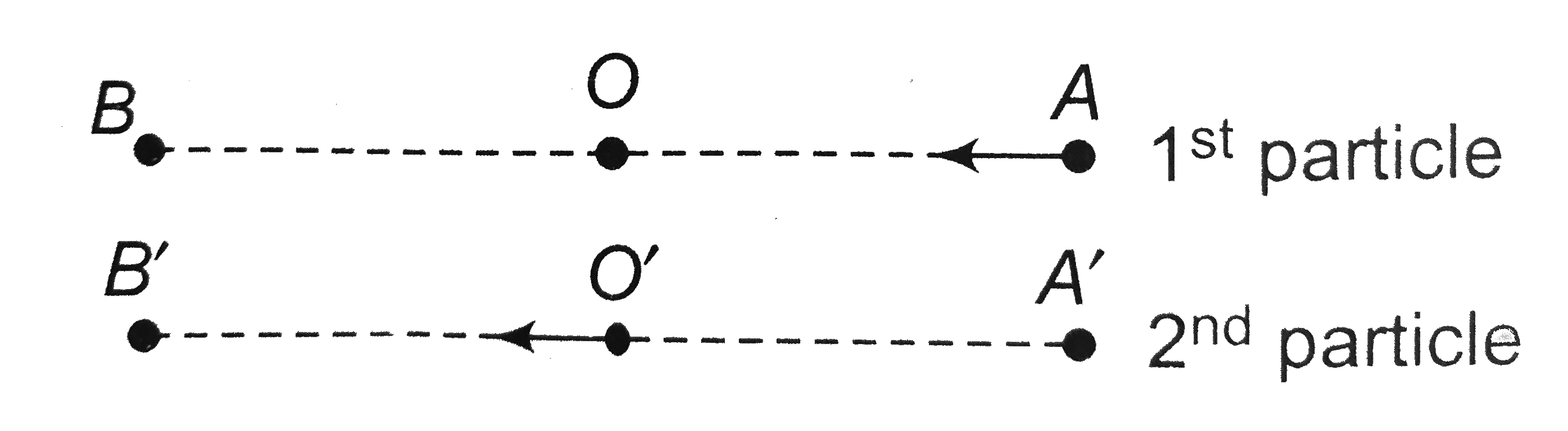 04:57View Solution
04:57View SolutionTwo particles execute `SHM` of same amplitude of `20 cm` with same period along the same line about the same equilibrium position. If phase difference is `pi//3` then the maximum distance between these two will be
02:22View SolutionA particle is moving in a circle with uniform speed its motion is
03:23View SolutionFor a particle simple harmonic motion determine the ratio of avarage acceleration of particle from external position to equilibruim position to the maximum acceleration
04:51View SolutionThe acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
02:13View SolutionThe equation of motion of a particle executing simple harmonic motion is `a+16pi^(2)x = 0` In this equation, a is the linear acceleration in `m//s^(2)` of the particle at a displacement x in meter. The time period in simple harmonic motion is
01:11View SolutionTwo simple harmonic motion are represented by equations
`y_(1) = 4 sin (10 t + phi)`
`y_(2) = 5 cos 10t`
What is the phase difference between their velocities ?02:13View SolutionA particle performs SHM with a period `T` and amplitude a. The mean velocity of particle over the time interval during which it travels `a//2` from the extreme position is
03:12View SolutionA particle performs simple hormonic motion with a period of 2 seconds. The time taken by it to cover a displacement equal to half of its amplitude from the mean position is
03:26View SolutionA particle performs `SHM` on x- axis with amplitude `A ` and time period `T` .The time taken by the particle to travel a distance `A//5` starting from rest is
03:21View SolutionTwo particles `P_(1)` and `P_(2)` are performing `SHM` along the same line about the same meabn position , initial they are at their position exterm position. If the time period of each particle is `12` sec and the difference of their amplitude is `12 cm` then find the minimum time after which the seopration between the particle becomes `6 cm`
02:54View SolutionA particle executes `SHM` of amplitude `A` and time period `T` The distance travelled by the particle in the during its phasde changes from `(pi)/(12)` to `(5 pi)/(12)` sin15=0.26,sin75=0.96
03:00View SolutionThe phase difference between two SHM `y_(1) = 10 sin (10 pi t + (pi)/(3))` and `y_(2) = 12 sin (8 pi t + (pi)/(4))` at `t = 0.5s` is
01:12View SolutionIf displacement `x` and velocity `v` related as
`4v^(2) = 25 - x^(2)m` in a `SHM` Then time period of given `SHM` is (consider SI unit)04:13View SolutionThe phase difference between the displacement and acceleration of a particle executing simple harmonic motion is
03:17View SolutionThe displecemen-time equation of a particle execitting `SHM` is `x = A sin (omega t + phi)` At time `t = 0` position of are position is `x = A//2` and it is moving along negative `x- direction` .Then the angle `phi` can be
04:02View SolutionThe phase difference between two particle executing `SHM` of the same amplitude and frequency along same straight line while pessing one another when going in apposition direction with equal displacement from then respectively straing about is is `2pi//3` if the prass if one particle is `pi//6` find the displecement at this instant amplitude is `A`
02:40View SolutionTime period `(T)` and amplitude `(A)` are same for two particle which undergoes `SHM` along the same line. At one particular instant one particle is at phase`(3pi)/(2)`and the other is at zero, while moving in the same direction. Find the time at which they will cross each other
01:41View Solution
Equation Of Shm , Phase And Comparing Shm With Uniform Circular Motion questions and complete solutions for chapter OSCILLATION AND SIMPLE HARMONIC MOTION of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS OSCILLATION AND SIMPLE HARMONIC MOTION
- AIIMS Questions
- Assertion Reasoning
- Chapter Test
- Equation Of Shm , Phase And Comparing Shm With Uniform Circular Motion
- NEET Questions
- Problems Based On Mixed Concepts
- Simple Pendulum And Different Cases Of Shm
- Spring Particle System
- Superposition Of Shm And Compound Pendulum
- Velocity , Acceleration And Energy Of Simple Harmonic Motion
