Complete Solutions to Problems Based On Mixed Concepts of chapter OSCILLATION AND SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATION AND SIMPLE HARMONIC MOTION |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A particle is performing a linear simple harmonic motion if the acceleration and the corresponding velocity of the particle are `a` and `v` respectively. Which of the following graph is correct?
View SolutionA pendulum has a period `T` for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.

View SolutionA particle is moving along the axis under the influnence of a force given by `F = -5x + 15`. At time `t = 0`, the particle is located at `x = 6` and having zero velocity it take `0.5` second to reach the origin for the first time. The equation of mnotion of the particle can be respected by
View SolutionIn the above question the mass of the particle is
View SolutionA particle executes simple harmonic motion according to the displacement equation `y = 10 cos(2 pi t + (pi)/(6))cm` where `t` is in second The velocity of the particle at `t = 1/6` second will be
View SolutionFind the distance covered by a particle from time `t = 0` to `t = 6` sec when the particle follow the movament according to `y = a cos ((pi)/(4))t`
View SolutionTwo very small having mass `m` are atteched to two masses rods of length `l` Now these rods are joined it form `V` like figure having angle `60^(@)` This assumility is new higest in a verticle plane so that it can rotan without any friction about a horizontal axis perpendicular in the plane of figure) as shown in the figure The period of small oscilation of this asseamble is
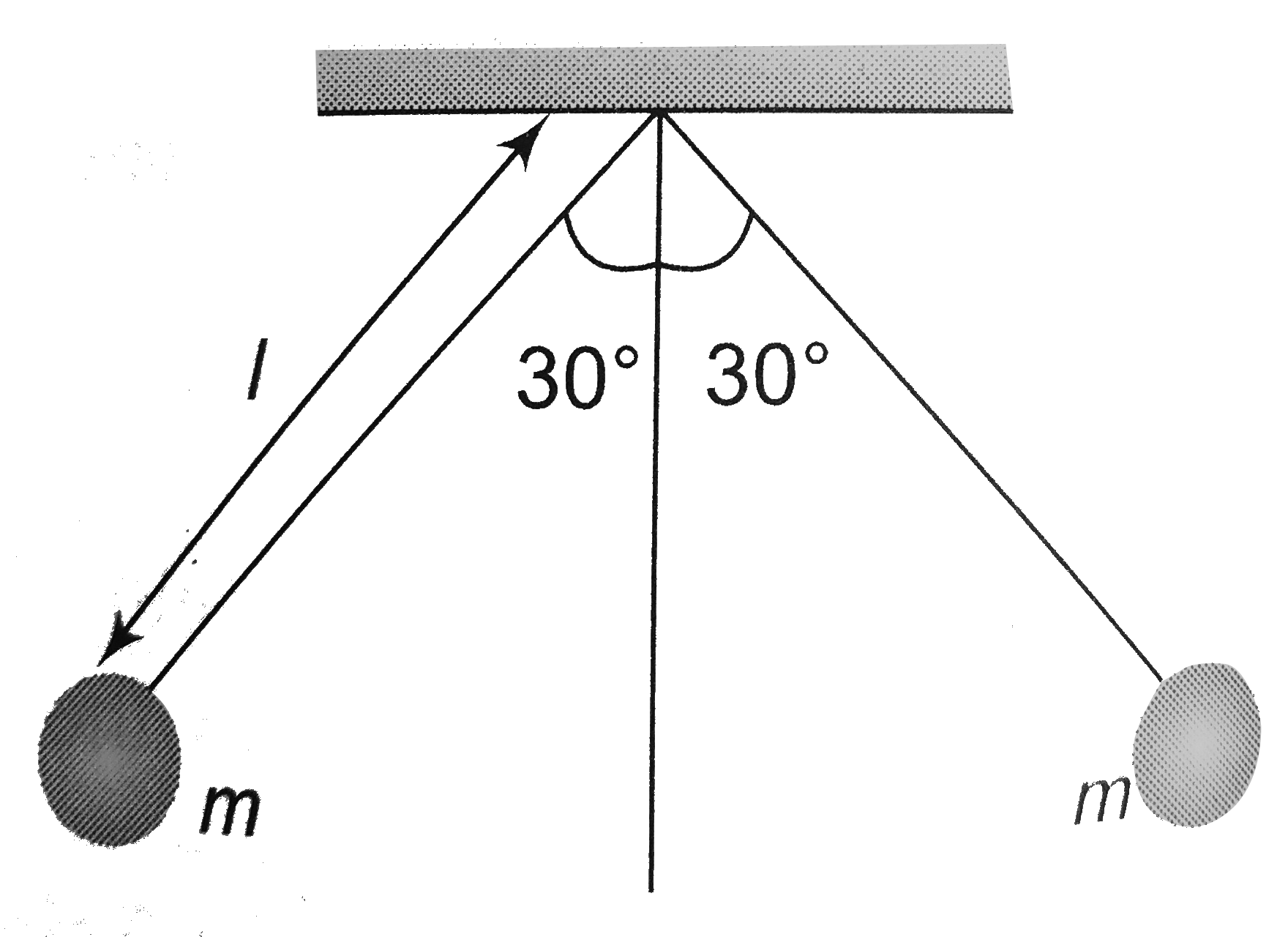
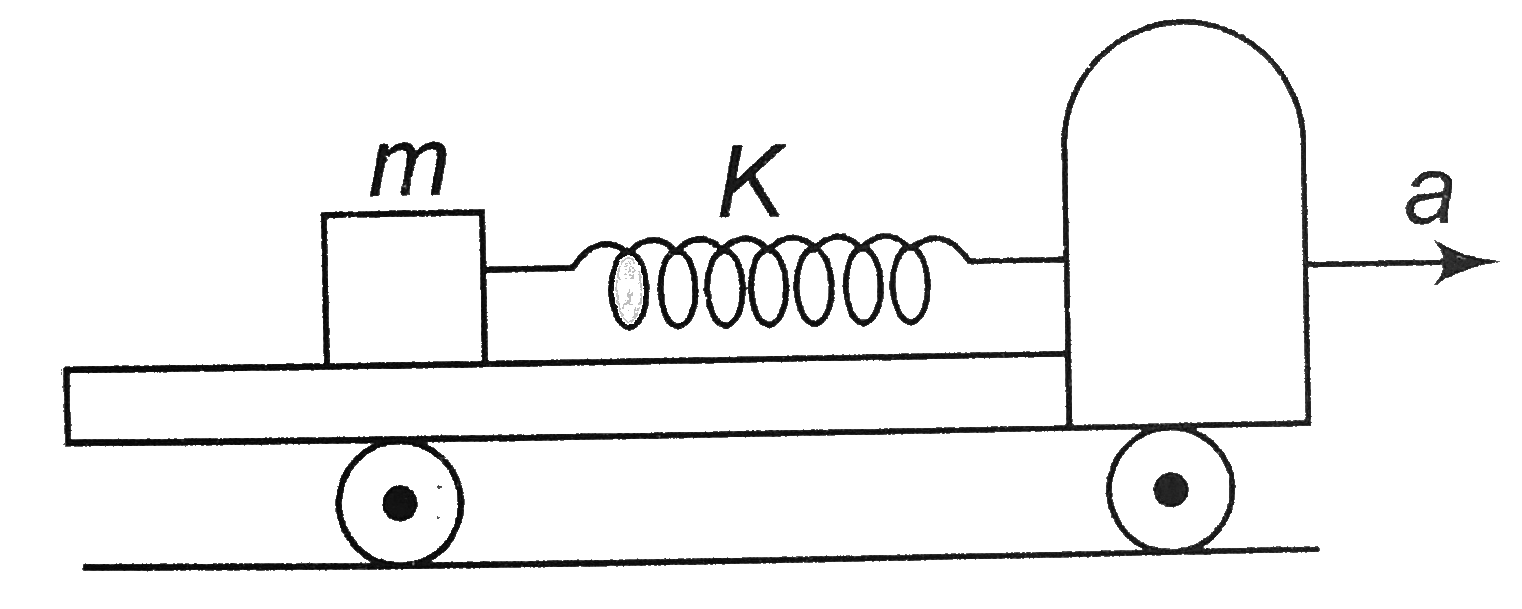
View SolutionOne end of an spring is connected with a smooth block with the other end with rear wall of a truck as shown in figure. initially, the system is at rest if track start to its accelerate with a constant acceleration then the block (relative to track)
View SolutionA particle free to move along the (x - axis) hsd potential energy given by `U(x)= k[1 - exp(-x^2)] for -o o le x le + o o`, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle moves along a straight line to follow the equation `ax^(2) + bv^(2) = k`, where `a, b` is and k are constant and `x` and and `x` axis coordirete and velocity of the particle respectively find the amplitude
View SolutionTwo particle of same time period `(T)` and amplitude undergo `SHM` along the same line with initial and phase of `pi//6`. If they start at the same point along the opposite directions. Find the time other which they will meet again for the first time
View SolutionAs time ` t = 0` one particle is at maximum position amplitude and the other is at half at the position amplitude Their amplitude and time period `T` are same if they are appoatules find the take by which they cross each other
View SolutionThe displacement function of a `S.H.M` is given by
`y = cos [(omega t + phi)]`
if at `t = 0` th displaxcement is `y = 1` on and velocity `cm s^(-1)` The value amplitude `(A in cm)` is
View SolutionA particle oscillation is given by `(f_(0)) = kpl^(2)` with for constant `k` and an amplitude A The maximum velocity during the oscillation a preperitiaonal to :
View SolutionA mass of `0.98kg` attached on a spring of constant `K = 100Nm^(1)` is hit by a bules of `20gm` moving with a velocity `20ms^(1)` horizontally The bullet gas ambated and system oscilation with the mass on horizontal and surface The amplitude of oscilation will be
View SolutionA uniform stick of mass `M` and length `L` is pivoted its come its ands are fast to two spring each of the constant `K`. In the position shown in figure the same through a small length when spring is display through a small angle of and released. The stick :
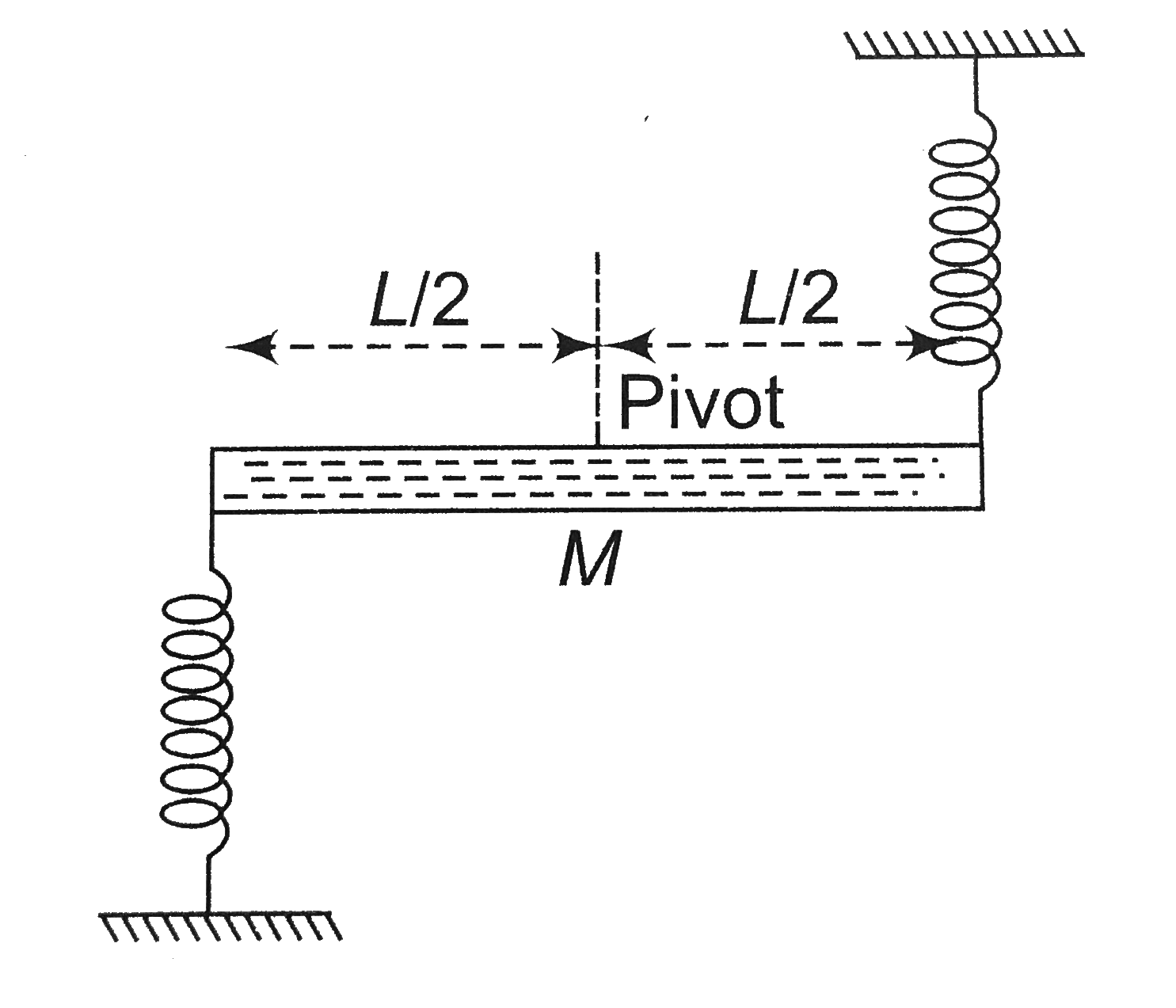
View SolutionThe potential energy of a particle of mass `1kg` in motion along the x- axis is given by: `U = 4(1 - cos 2x)`, where `x` in metres. The period of small oscillation (in sec) is
View SolutionA particle executing `SHM` while moving from executy it found at distance `x_(1) x_(2)` and `x_(2)` from comes at the and of three successive second The period of oscilation is
where `theta = cos^(-1)((x_1 + x_2)/(2x_(2)))`
View SolutionA particle of mass `m` is executing oscillations about origin on the x axis amplitude A its potential energy is given as`U(x) = beta x^(4)` where `beta` is constant x cooridirate of the particle where the potential energy is one third of the kinetic energy is
View SolutionA body is executing a simple harmonic motion such that its potential energy is `U_(1) `at `U_(2)at y` When the displacement is `x+y` the potential energy will be
View SolutionA bead of mass `m` can slide on a frictionless wire as shown in figure Because of the given shape of the wire near `p` the bottom point , it can be approximated as near `p` the potential energy of the bead is given `U = cx^(2)` where `c` is a constant and `x` is measured from `p` The bead if displacement slightly from point `p` will oscillate about `p` The period of oscillation is
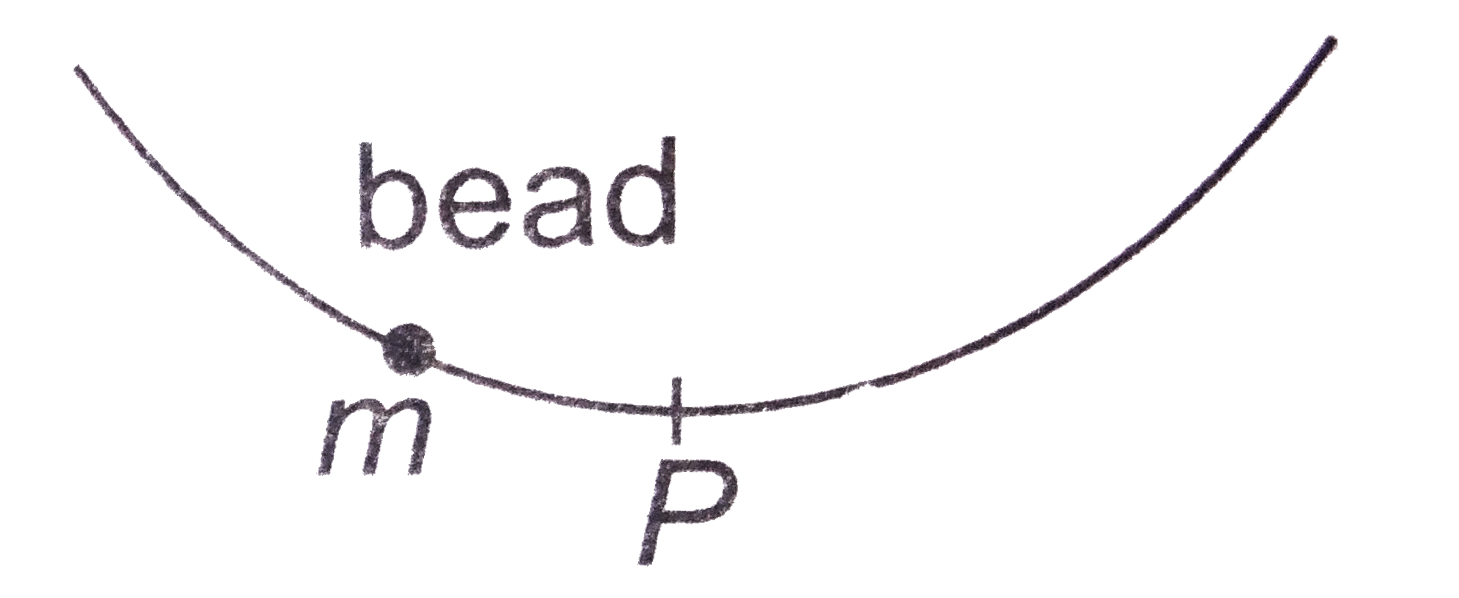
View SolutionA horizontal spring -block system of mass `2kg` executes `S.H.M` when the block is passing through its equilibrium positiojn an object of mass `1kg` is put on it the two move togather The new amplitude of vibration is `(A` being its initial amplitude)
View SolutionAn air chamber of volume `V` has a long of cross sectional area `A`. A ball of mass `m` is fixed sympthlly in the track The ball modulus of air is `B` ball is pressed down slightly and released, the time period of the oscillation is
View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter OSCILLATION AND SIMPLE HARMONIC MOTION of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS OSCILLATION AND SIMPLE HARMONIC MOTION
- AIIMS Questions
- Assertion Reasoning
- Chapter Test
- Equation Of Shm , Phase And Comparing Shm With Uniform Circular Motion
- NEET Questions
- Problems Based On Mixed Concepts
- Simple Pendulum And Different Cases Of Shm
- Spring Particle System
- Superposition Of Shm And Compound Pendulum
- Velocity , Acceleration And Energy Of Simple Harmonic Motion