Complete Solutions to NEET Questions of chapter OSCILLATION AND SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATION AND SIMPLE HARMONIC MOTION |
| A2Z | NEET Questions |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
There is a body having mass `m` and performinf `SHM` amplitude a There is a restroring force `F = - Ks` where `x` is the displacement The total energy of body depends upon
View SolutionA hollow sphere filled with water through a small body in it is then hung by a long thread and made to oscillation As the water slowly force end of the hole at the bottom the period of oscillation will
View SolutionThe kinetic energy and the potential energy of a particle executing `SHM` are equal The ratio of its displacement and amplitude will be
View SolutionDisplacement between maximum potential energy position energy positionand maximum ki9netic energy position for a particle executing `S.H.M` is
View SolutionA mass `m` is suspended separately by two different springs of spring constant `k_(1)` and `k_(2)` given the time period `t_(1)` and `t_(2)` respectively. If the same mass `m` is shown in the figure then time period `t` is given by the relation

View SolutionA particle doing simple harmoonic motion amplitude `= 4 cm` time peiod `= 12sec` The ratio between time taken by it in going from its mean position to `2cm ` and from `2cm` to exterme position is
View SolutionThe potential energy of a harmonic oscillation when is half way to its and end point is (where `E` it’s the total energy)
View SolutionThe time period of a mass suspended from a spring is `T` if the spring is cut in to equal part and the same mass is suspended from one of the pert then the time period will be
View SolutionIn case of a force vibration the resonance wave becomes very step when the
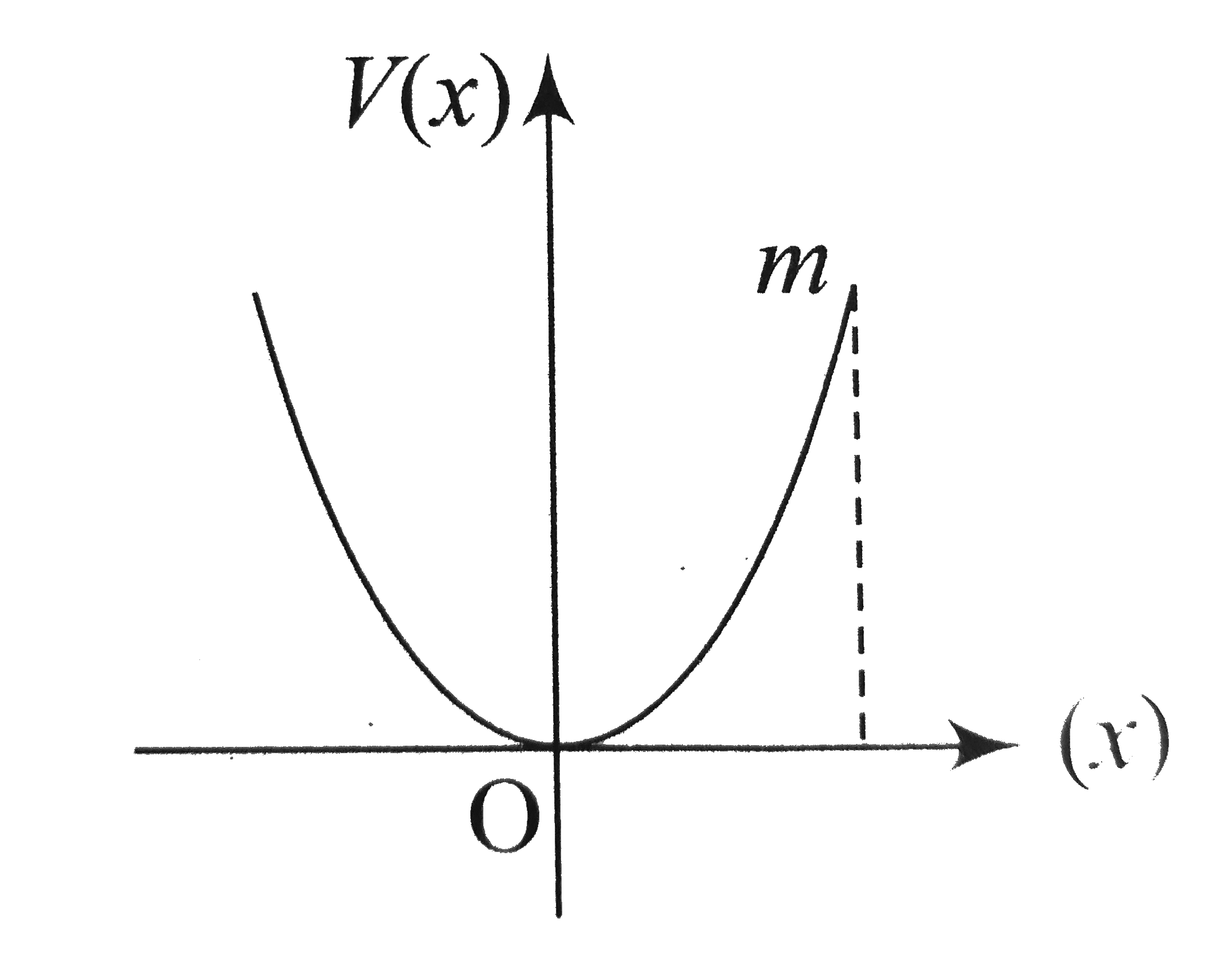
View SolutionA particle of mass `m` oscillates with simple harmonic motion between points `x_(1)` and `x_(2)` the equilibrium position being `O` its potential energy in plotted it will be as given bellow in the graph
View SolutionWhich one of the following statement is true for the speed `v` and the acceleration a of a particle executing simple harmonic motion?
View SolutionTwo spring of spring constant `k_(1)` and `k_(2)` are joined in series The effective spring constant of the combination is given by
View SolutionThe resultant of two rectangular simple harmonic motion of the same frequency and unequal amplitude but differing in phase by `pi//2` is
View SolutionA particle executing simple harmonic motion of amplirtude `5cm` has maximum speed of `31.4 cm//s` The frequency of its oscillation is
View SolutionThe potential energy of a spring when stretched by `2cm` is U. if the spring is stretched by `8cm` the potential energy in it is
View SolutionA rectangular block of mass `m` and area of cross a small vertical displacement from equilibrium it undergoes oscillation with a time period `T` then
View SolutionThe pahse difference between the instantaneous veliocity and acceleration of a particle executing simple harmonic motion is
View SolutionThe particle executing simple harmonic motion has a kinetic energy `K_(0) cos^(2) omega t`. The maximum values of the potential energy and the energy are respectively
View SolutionA mass of `2.0kg`is put on a that pan attached to a vertical spring fixed on the ground as shown in the figure The mass of the spring and the pen is negligible the mass executing a simple harmonic motion The spring constant is `200N//m` what should be the minimum amplitude of the motion so that the mass get detached from the part? `(Taking g = 10m//s^(2))`
View SolutionA particle executes simple harmonic oscillation with an amplitude `a`. The period of oscillations is `T`. The minimum time taken by the particle to travel half to the amplitude from the equliibrium position is
View SolutionTwo simple harmonic motion of angular frequency `100and 1000 rads^(-1)` have the same displacement amplitude The ratio of their maximum acceleration is
View SolutionA point simple harmonic oscillation of the period and the equation of motion is given by `x a sin (omega t + pi //6)` after the step of friction of the time period the velocity of the part will be equal to half of its maximum velocity?
View SolutionA simple pendulum performs simple harmonic motion about `x = 0` with an amplitude a and time period `T` speed of the pendulum at `x = a//2` will be
View SolutionWhich one of the following equation at the repressents simple harmonic motion ?
View SolutionA block of mass `m` attached in the lower and vertical spring The spring is hung from a calling and force constant value `k` The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
View SolutionThe displacement of a particle along the x- axis it given by `x = a sin^(2) omega t` The motion of the particle corresponds to
View SolutionThe period of oscilation of a mass `M` suspended a spring negligible mass is `T` if along with it and there mass `M` is also suspended the period of oscillation now be
View SolutionA particle of mass `m` is released from rest and follow a particle part as shown Assuming that the displacement of the mass from the origin is small which graph correctly depicts the position of the particle as a function of time?
View SolutionOut of the following functions representing motion of a particle which represents SHM
I. `y = sin omega t - cos omega t`
II. `y = sin^(3)omega t`
III. `y = 5 cos ((3 pi)/(4)-3 omega t)`
IV. `y = 1 + omega t + omega^(2)t^(2)`
View SolutionTwo pearticle are oscillation along two close parallel straght lines side by side with the same frequency and amplitude They pass each other moving in opposite directions when their displacement is half of the on a stright line perpendicular to the part of the two particle The phase difference is
View SolutionThe damping force on an oscillator is directly proportional to the velocity .The units of the constant of proportionality are
View SolutionThe equation of a simple harmonic wave is given by
`y = 3 sin"(pi)/(2) (50t - x)`
where `x` and `y` are in meters and `x` is in second .The ratio of maximum particle velocity to the wave velocity is
View SolutionThe oscillation of a body on a smooth horizontal surface is represented by the equation
`X = A cos (omegat)`
which one of the following graph shown correctly the variation a with `t`?
View Solutionwhen two displacements represented by `y_(1) = a sin(omega t)` and `y_(2) = b cos (omega t)` are superimposed the motion is
View Solution(a) The motion of the particle in simple harmonic motion is given by `x = a sin omega t`. If its speed is `u`, when the displacement is `x_(1)` and speed is `v`, when the displacement is `x_(2)`, show that the amplitude of the motion is
`A = [(v^(2)x_(1)^(2) - u^(2)x_(2)^(2))/(v^(2) - u^(2))]^(1//2)`
(b) A particle is moving with simple harmonic motion is a straight line. When the distance of the particle from the equilibrium position has the values ` x_(1)` and `x_(2)` the corresponding values of velocity are `u_(1)` and `u_(2)`, show that the period is
`T = 2pi[(x_(2)^(2) - x_(1)^(2))/(u_(1)^(2) - u_(2)^(2))]^(1//2)`
View SolutionA particle is executing a simple harmonic motion its maximum acceleration is a and maximum velocity is `beta` .Then its time of vibration will be
View SolutionA body of mass `m` is atteched to the lower end of a spring whose upper end is fixed .The spring has negaligible mass .When the mass `m` is slightly puylled down and released it oscillation with a time period of `3 s` when the mass `m` is increased by `1kg` time period of oscillations becomes `5s` The value of `m` in `kg` is
View SolutionA particle executies linear simple harmonic motion with an amplitude `3cm` .When the particle is at `2cm` from the mean position , the magnitude of its velocity is equal to that of acceleration .The its time period in seconds is
View SolutionA pendulum is hung the roof of a sufficiently high huilding and is moving freely to and fro like a simple harmonic oscillator .The acceleration of the bob of the pendulum is `20m//s^(2)` at a distance of `5m` from the meanposition .The time period of oscillation is
View Solution
NEET Questions questions and complete solutions for chapter OSCILLATION AND SIMPLE HARMONIC MOTION of A2Z PHYSICS (HINGLISH) of Class 11
All Exercises from A2Z Class 11 PHYSICS OSCILLATION AND SIMPLE HARMONIC MOTION
- AIIMS Questions
- Assertion Reasoning
- Chapter Test
- Equation Of Shm , Phase And Comparing Shm With Uniform Circular Motion
- NEET Questions
- Problems Based On Mixed Concepts
- Simple Pendulum And Different Cases Of Shm
- Spring Particle System
- Superposition Of Shm And Compound Pendulum
- Velocity , Acceleration And Energy Of Simple Harmonic Motion