Complete Solutions to All Questions of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| ARIHANT MASTER PROBLEM | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let `vecu` be the initial velocity of a particle and `vecF` be the resultant force acting on it . Describe the path that the particle can take if
(a) `vecu xx vecF = 0 "and" vecF = "constant"`
(b) `vecu.vecF = 0 "and" vecF = "constant"`
In which case can the particle retrace its path .03:16View SolutionA ball is projected vertically up from the floor of a room. The ball experiences air resistance that is proportional to speed of the ball. Just before hitting the ceiling the speed of the ball is 10 m/s and its retardation is 2g. The ball rebounds from the ceiling without any loss of speed and falls on the floor 2s after making impact with the ceiling. How high is the ceiling? Take `g = 10 m//s^(2)`.
03:28View SolutionA small body of super dense material, whose mass is half the mass of the earth (but whose size is very small compared to the size of the earth), starts from rest at a height H above the earth’s surface, and reaches the earth’s surface in time t. Calculate time t assuming that H is very small compared to the radius of the earth. Acceleration due to gravity near the surface of the earth is g.
02:46View SolutionN identical carts are connected to each other using strings of negligible mass. A pulling force F is applied on the first cart and the system moves without friction along the horizontal ground. The tension in the string connecting `4^(th) "and" 5^(th)` cart is twice the tension in the string connecting `8^(th) "and" 9^(th)` cart. Find the total number of carts (N) and tension in the last string.
 03:43View Solution
03:43View SolutionA toy cart has mass of 4 kg and is kept on a smooth horizontal surface. Four blocks A, B, C and D of masses 2 kg, 2 kg, 1 kg and 1 kg respectively have been placed on the cart. A horizontal force of F = 40 N is applied to the block A (see figure). Find the contact force between block D and the front vertical wall of the cart.
 02:13View Solution
02:13View SolutionIn the arrangement shown in the figure the system is in equilibrium. Mass of the block A is M and that of the insect clinging to block B is m. Pulley and string are light. The insect loses contact with the block B and begins to fall. After how much time the insect and the block B will have a separation L between them.
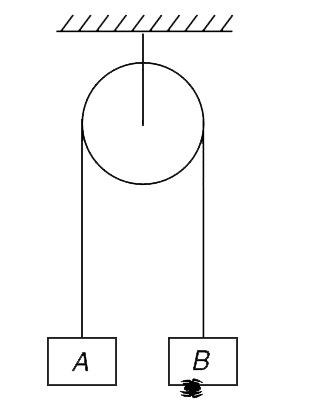 04:05View Solution
04:05View SolutionTwo blocks of equal mass, M each, are connected to two ends of a massless string passing over a massless pulley. On one side of the string there is a bead of mass `(M)/(2)` .
(a) When the system is released from rest the bead continues to remain at rest while the two blocks accelerate. Find the acceleration of the blocks.
(b) Find the acceleration of the two blocks if it was observed that the bead was sliding down with a constant velocity relative to the string.
 05:23View Solution
05:23View SolutionA pulley is mounted on a stand which is placed over a weighing scale. The combined mass of the stand and the pulley is `M_(0)`. A light string passes over the smooth pulley and two masses m and M (gt m) are connected to its ends (see figure). Find the reading of the scale when the two masses are left free to move.
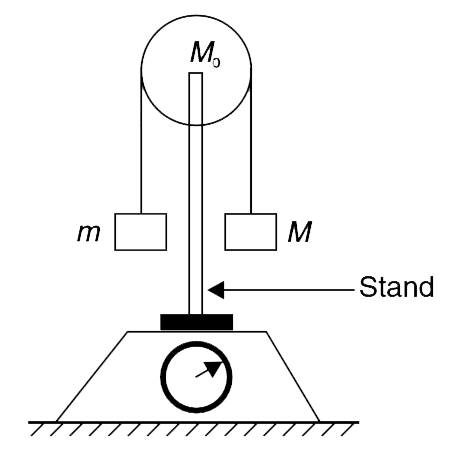 04:01View Solution
04:01View SolutionIn the given arrangement, all strings and pulleys are light. When the system was released it was observed that M and `m_(0)` do not move. Find the masses M and `m_(0)` in terms of `m_(1) "and" m_(2)`. Find the acceleration of all the masses if string is cut just above `m_(2)`.
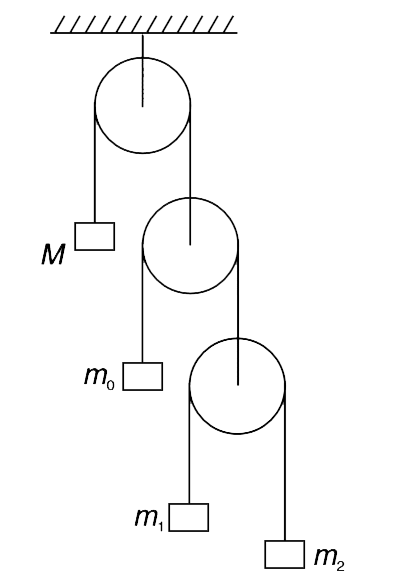 01:12View Solution
01:12View SolutionA block slides down a frictionless plane inclined at an angle `theta`. For what value of angle `theta` the horizontal component of acceleration of the block is maximum? Find this maximum horizontal acceleration.
01:00View SolutionA tall elevator is going up with an acceleration of `a = 4 m//s^(2)`. A 4 kg snake is climbing up the vertical wall of the elevator with an acceleration of a. A 50 g insect is riding on the back of the snake and it is moving up relative to the snake at an acceleration of a. Find the friction force between the elevator wall and the snake. Assume that the snake remains straight.
02:56View SolutionDue to air drag the falling bodies usually acquire a constant speed when the drag force becomes equal to weight. Two bodies, of identical shape, experience air drag force proportional to square of their speed `(F_("drag") = kv^(2)`, k is a constant). The mass ratio of two bodies is `1 : 4`. Both are simultaneously released from a large height and very quickly acquire their terminal speeds. If the lighter body reaches the ground in 25 s, find the approximate time taken by the other body to reach the ground.
03:27View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
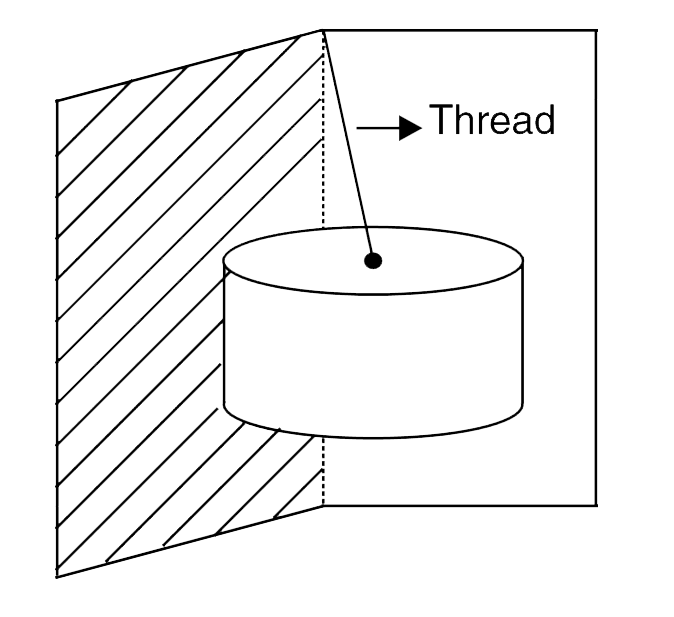 04:34View Solution
04:34View SolutionA rod of mass M and length L lies on an incline having inclination of `theta = 37^(@)`. The coefficient of friction between the rod and the incline surface is `mu = 0.90`. Find the tension at the mid point of the rod.
04:03View SolutionA ball of mass M is in equilibrium between a vertical wall and the inclined surface of a wedge. The inclination of the wedge is `theta = 45^(@)` and its mass is very small compared to that of the ball. The coefficient of friction between the wedge and the floor is `mu` and there is no friction elsewhere. Find minimum value of `mu` for which this equilibrium is possible
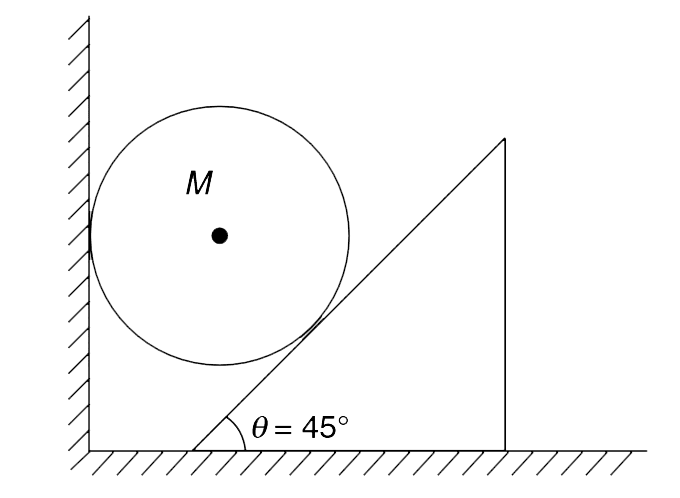 05:03View Solution
05:03View SolutionA pendulum has a bob connected to a light wire. Bob ‘A’ is in equilibrium in the position shown. The string is horizontal and is connected to a block B resting on a rough surface. The block B is on verge of sliding when `theta = 60^(@)`.
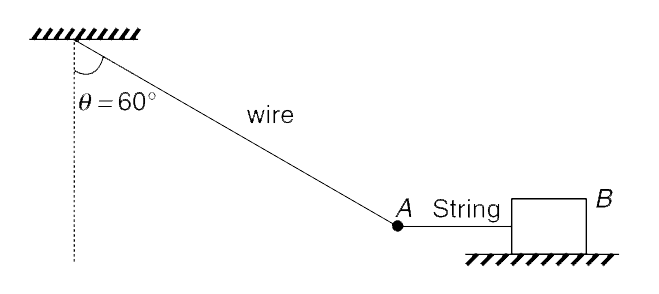
(a) Is equilibrium possible if `theta` were `70^(@)`?
(b) With `theta = 60^(@)`, calculate the ratio of tension in the pendulum wire immediately after the string is cut to the tension in the wire before the string is cut.04:04View SolutionTwo blocks of equal mass have been placed on two faces of a fixed wedge as shown in figure. The blocks are released from position where centre of one block is at a height h above the centre of the other block. Find the time after which the centre of the two blocks will be at same horizontal level. There is no friction anywhere.
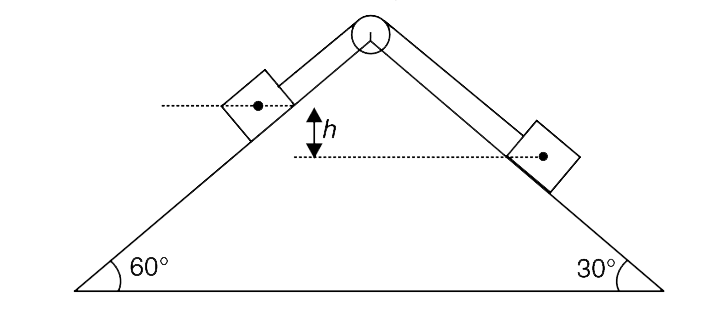 04:19View Solution
04:19View SolutionIn the system shown in the figure, all surfaces are smooth. Block A and B have mass m each and mass of block C is 2 m. All pulleys are massless and fixed to block C. Strings are light and the force F applied at the free end of the string is horizontal. Find the acceleration of all three blocks.
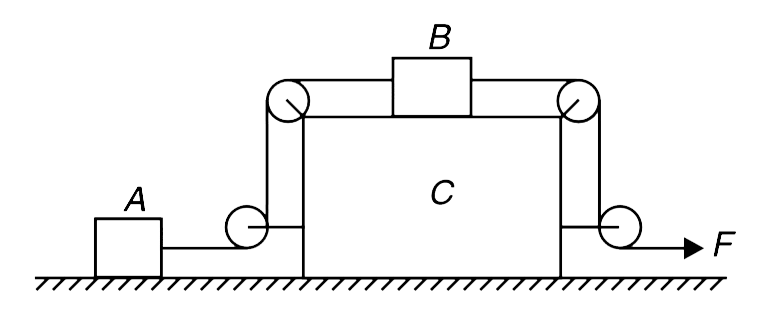 02:03View Solution
02:03View SolutionA particle of mass M rests on a rough inclined plane at an angle q to the horizontal`("sin" theta = (4)/(5))`. It is connected to another mass m as shown in fig. The pulley and string are light. The largest value of m for which equilibrium is possible is M. Find the smallest value of m for which equilibrium is possible
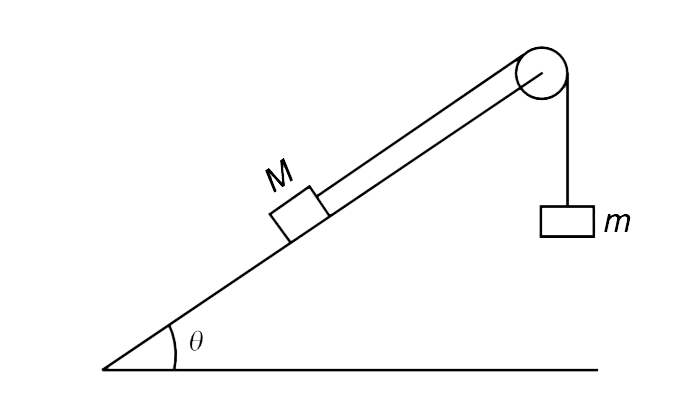 10:04View Solution
10:04View SolutionA small body A starts sliding down from the top of a wedge (see fig) whose base is equal to l. The coefficient of friction between the body and wedge surface is `mu= 1.0`. At what value of angle q will the time of sliding be least?
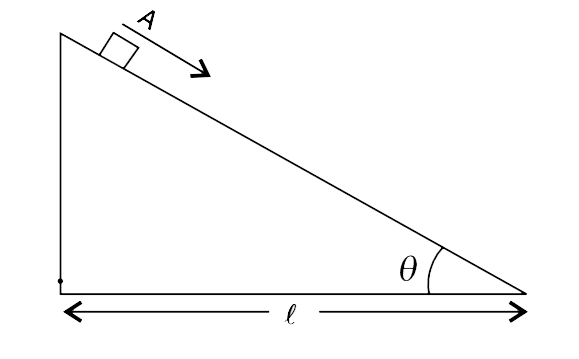 01:48View Solution
01:48View SolutionThree blocks A, B and C each of mass m are placed on a smooth horizontal table. There is no friction between the contact surfaces of the blocks as well. Horizontal force F is applied on each of A and B as shown. Find the ratio of normal force applied by the table on the three blocks (i.e., `R_(A) : R_(B) : R_(C)`). Take `F = (mg)/(2sqrt3)`
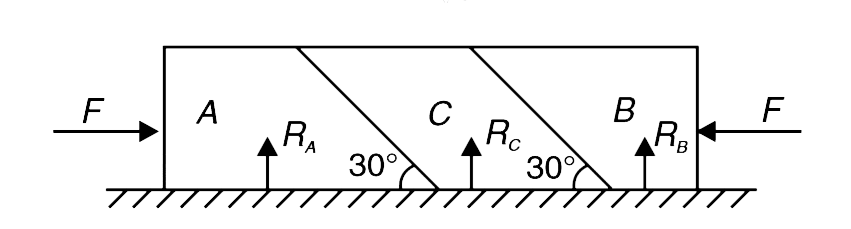 08:17View Solution
08:17View SolutionA U shaped container has uniform cross sectional area S. It is suspended vertically with the help of a spring and two strings A and B as shown in the figure. The spring and strings are light. When water (density = d ) is poured slowly into the container it was observed that the level of water remained unchanged with respect to the ground. Find the force constant of the spring.
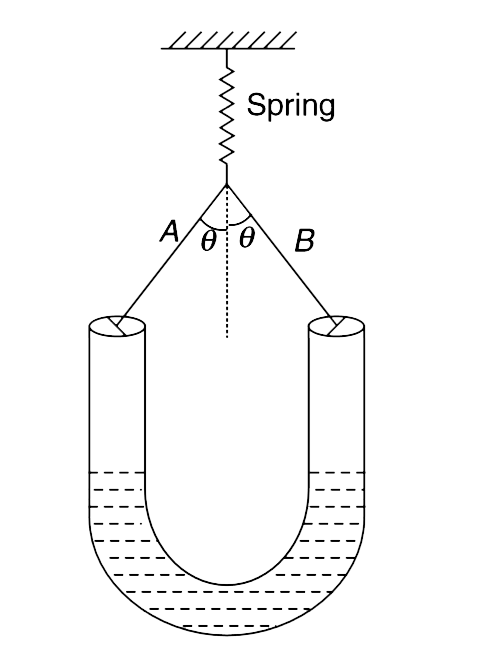 03:05View Solution
03:05View SolutionA uniform light spring has unstretched length of 3.0 m. One of its end is fixed to a wall. A particle of mass m = 20 g is glued to the spring at a point 1.0 m away from its fixed end. The free end of the spring is pulled away from the wall at a constant speed of 5 cm/s. Assume that the spring remains horizontal (i.e., neglect gravity). Force constant of spring = 0.6 N / cm.
(a) With what speed does the particle of mass m move?
(b) Find the force applied by the external agent pulling the spring at time 2.0 s after he started pulling.
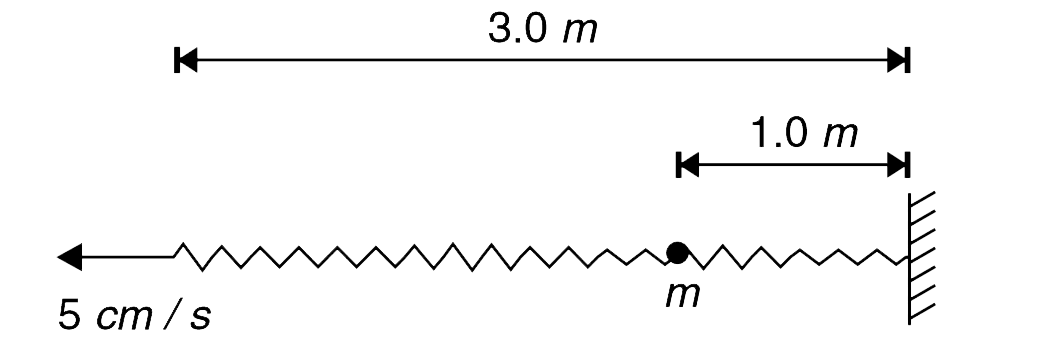 03:27View Solution
03:27View SolutionIt was observed that a small block of mass m remains in equilibrium at the centre of a vertical square frame, which was accelerated. The block is held by two identical light strings as shown. [Both strings are along the diagonal]
(a) Which of 1, 2, 3 & 4 is/are possible direction/s of acceleration of the frame for block to remain in equilibrium inside it?
(b) Find the acceleration of the frame for your answers to question (a).
 05:10View Solution
05:10View SolutionIn an emergency situation while driving one has tendency to jam the brakes, trying to stop in shortest distance. With wheels locked, the car slides and steering get useless. In ABS system the electronic sensors keep varying the brake pressure so as to keep the wheels rolling (without slipping) while ensuring that the friction remains limiting. Your friend has an old car with good brakes. He boasts saying that all the four wheels of his car get firmly locked and stop rotation immediately after the brakes are applied. You know that your new car which has a computerized anti lock braking system (ABS) is much safer. How will you convince your friend?
In a typical situation, car without ABS needs 20 m as minimum stopping distance. Under identical conditions, what minimum distance a car with ABS would need to stop? Coefficient of kinetic friction between tyre and road is `25%` less than the coefficient of static friction05:16View SolutionA table cloth of length L is lying on a table with one of its end at the edge of the table. A block is kept at the centre of the table cloth. A man pulls the end of the table cloth horizontally so as to take it off the table. The cloth is pulled at a constant speed `V_(0)`. What can you say about the coefficient of friction between the block and the cloth if the block remains on the table (i.e., it does not fall off the edge) as the cloth is pulled out.
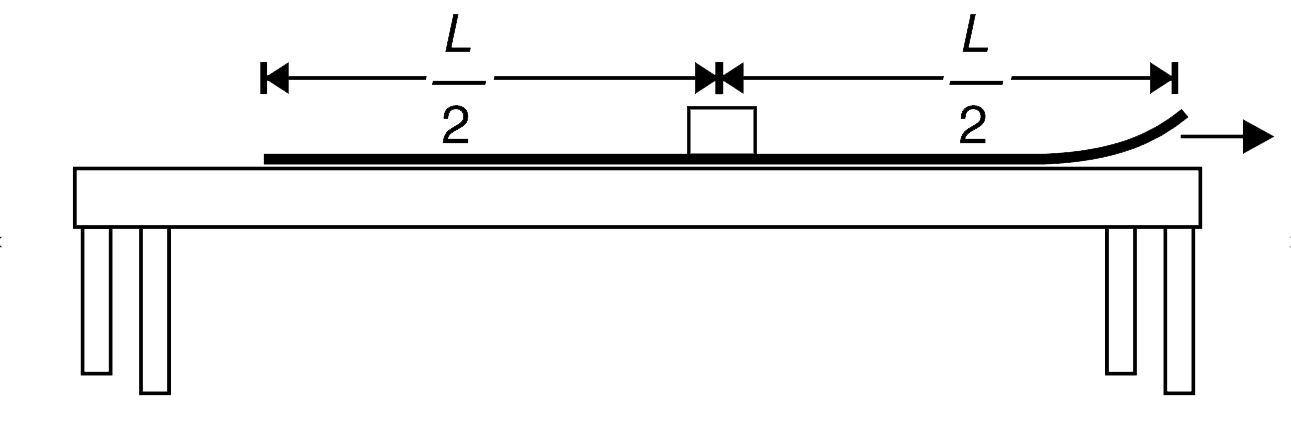 03:39View Solution
03:39View SolutionA block rests on a horizontal surface. A horizontal force F is applied to the block. The acceleration (a) produced in the block as a function of applied force (F) has been plotted in a graph (see figure). Find the mass of the block.
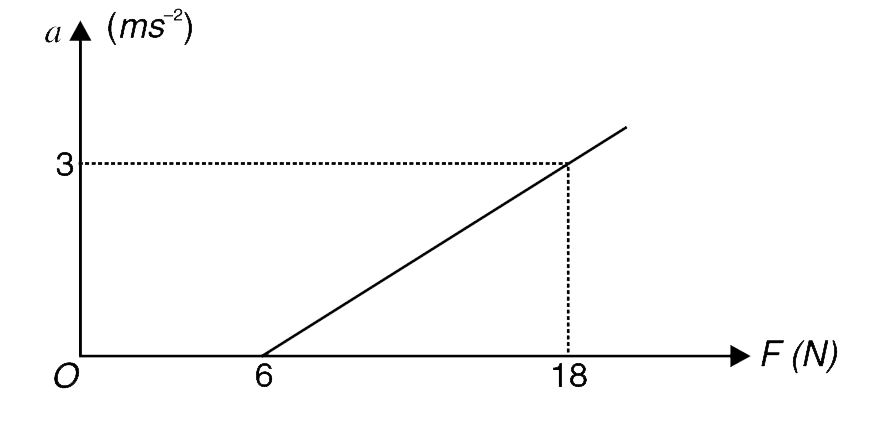 01:26View Solution
01:26View SolutionRepeat the last problem if the graph is as shown below.
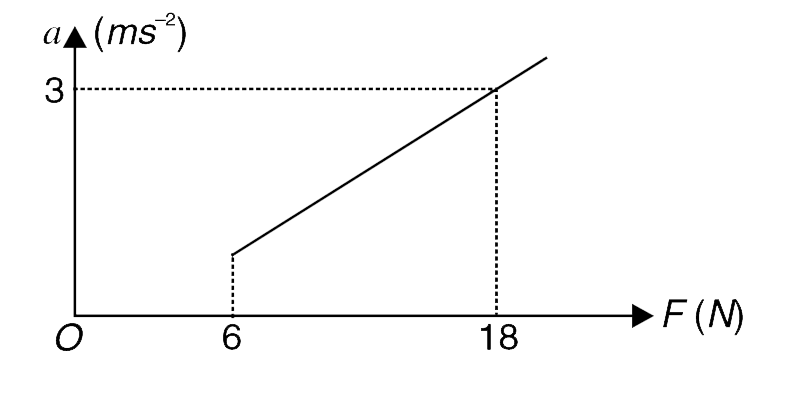 03:10View Solution
03:10View SolutionIn the system shown in the figure, the string is light and coefficient of friction between the 10 kg block and the incline surface is `mu = 0.5`. Mass of the hanger, H is 0.5 kg. A boy places a block of mass m on the hanger and finds that the system does not move. What could be values of mass m?
`"tan"37^(@) = (3)/(4) "and" g = 10m//s^(2)`
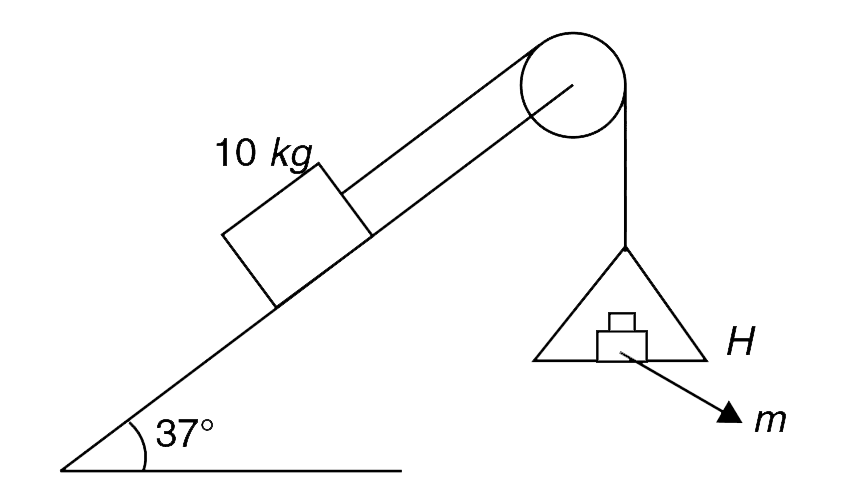 04:19View Solution
04:19View SolutionA disc of mass m lies flat on a smooth horizontal table. A light string runs halfway around it as shown in figure. One end of the string is attached to a particle of mass m and the other end is being pulled with a force F. There is no friction between the disc and the string. Find acceleration of the end of the string to which force is being applied.
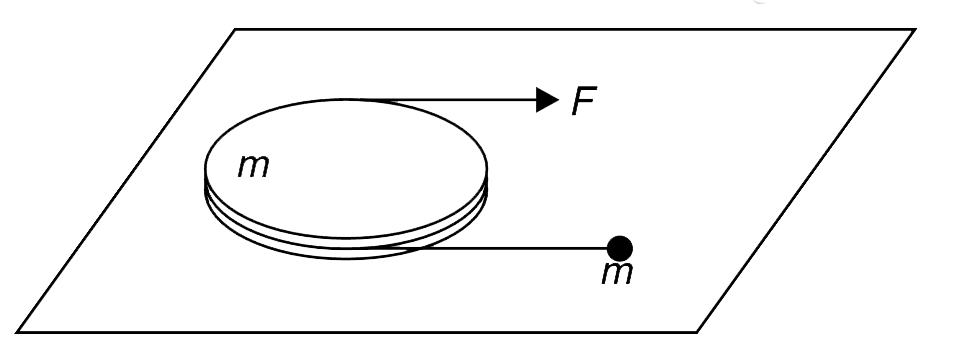 02:36View Solution
02:36View Solution(i) A spinning disk has a hole at its centre. The surface of the disk is horizontal and a small block A of mass m = 1 kg is placed on it.

Block A is tied to a light inextensible string, other end of which passes through the hole and supports another block B of mass M = 2 kg. The coefficient of friction between A and the disk surface is 0.5. It was observed that the disk is spinning with block A remaining at rest relative to the disk. Block B was found to be stationary. It was estimated that length of horizontal segment of the string (r) was anywhere between 1.0 m to 1.5 m. With this data what estimate can be made about the angular speed `(omega)` of the disk. `[g = 10 m//s^(2)`] (ii) A spring has force constant equal to `k = 100 Nm^(–1)`. Ends of the spring are joined to give it a circular shape of radius R = 20 cm. Now the spring is rotated about its symmetry axis (perpendicular to its plane) such that the circumference of the circle increases by `1%`. Find the angular speed `(omega)`. Mass of one meter length of the spring is `lambda = 0.126 gm^(–1)`.08:27View SolutionTwo particles of mass `m_(1) "and" m_(2)` are in space at separation `vecr` [vector from `m(1)` to `m_(2)`]. The only force that the two particles experience is the mutual gravitational pull. The force applied by `m_(1) "on" m_(2) "is" vecF `. Prove that `mu(d^(2)vecr)/(dt^(2)) = vecF` where `mu"(m_(1)m_(2))/(m_(1) + m_(2))` is known as reduced mass for the two particle system .
 03:34View Solution
03:34View SolutionSix identical blocks – numbered 1 to 6 – have been glued in two groups of three each and have been suspended over a pulley as shown in fig. The pulley and string are massless and the system is in equilibrium. The block 1, 2, 3, and 4 get detached from the system in sequence starting with block 1. The time gap between separation of two consecutive block (i.e., time gap between separation of 1 and 2 or gap between separation of 2 and 3) is `t_(0)`. Finally, blocks 5 and 6 remain connected to the string.
(a) Find the final speed of blocks 5 and 6.
(b) Plot the graph of variation of speed of block 5 with respect to time, Take t = 0 when block 1 gets detached.
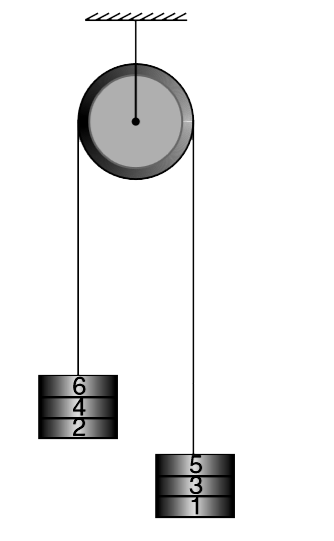 05:40View Solution
05:40View SolutionTwo strange particles A and B in space, exert no force on each other when they are at a separation greater than `x_(0) = 1.0` m. When they are at a distance less than `x_(0)`, they repel one another along the line joining them. The repulsion force is constant and does not depend on the distance between the particles. This repulsive force produces an acceleration of `6 ms^(–2)` in A and `2 ms^(–2)` in B when the particles are at separation less than `x_(0)`. In one experiment particle B is projected towards A with a velocity of `2 ms^(–1)` from a large distance so as to hit A head on. The particle A is originally at rest and the system of two particles do not experience any external force.
(a) Find the ratio of mass of A to that of B.
(b) Find the minimum distance between the particles during subsequent motion. (c) Find the final velocity of the two particles.09:47View SolutionA light string passing over a smooth pulley holds two identical buckets at its ends. Mass of each empty bucket is M and each of them holds M mass of sand. The system was in equilibrium when a small leak developed in bucket B (take this time as t = 0). The sand leaves the bucket at a constant rate of `mu` kg/s. Assume that the leaving sand particles have no relative speed with respect to the bucket (it means that there is no impulsive force on the bucket like leaving exhaust gases exert on a rocket). Find the speed `(V_(0))` of the two bucket when B is just empty.
 05:23View Solution
05:23View SolutionA chain is lying on a smooth table with half its length hanging over the edge of the table [fig(i)]. If the chain is released it slips off the table in time t1. Now, two identical small balls are attached to the two ends of the chain and the system is released [fig(ii)]. This time the chain took `t_(2)` time to slip off the table. Which time is larger, `t_(1)` or `t_(2)`?
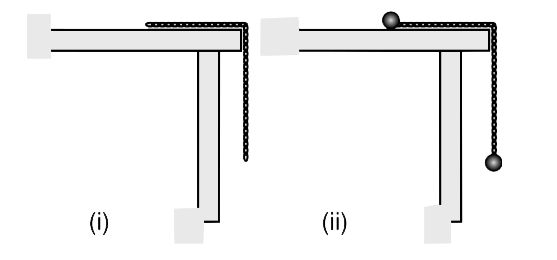 04:02View Solution
04:02View SolutionA triangular wedge W having mass M is placed on an incline plane with its face AB horizontal. Inclination of the incline is `theta`. On the flat horizontal surface of the wedge there lies an infinite tower of rectangular blocks. Blocks 1, 2, 3, 4 ………. have masses `M , (M)/(2) , (M)/(4) , (M)/(8)` ......... respectively . All surfaces are smooth. Find the contact force between the block 1 and 2 after the system is released from rest. Also find the acceleration of the wedge.
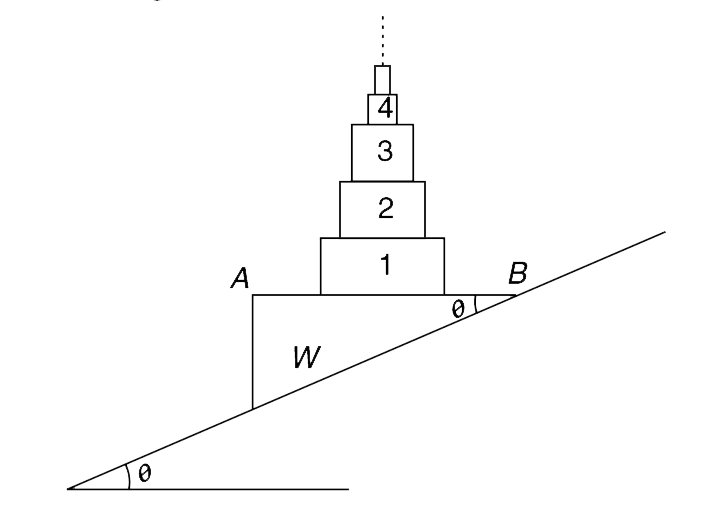 08:01View Solution
08:01View SolutionIn the system shown in fig, mass of the block is `m_(1) = 4` kg and that of the hanging particle is `m_(2) = 1` kg. The incline is fixed and surface is smooth. Block is initially held at the top of the incline and the particle hangs a distance d = 2.0 m below it. [Assume that the block and the particle are on same vertical line in this position]. System is released from this position. After what time will the distance between the block and the particle be minimum ? Find this minimum distance. [ `g = 10 m//s^(2)`.]
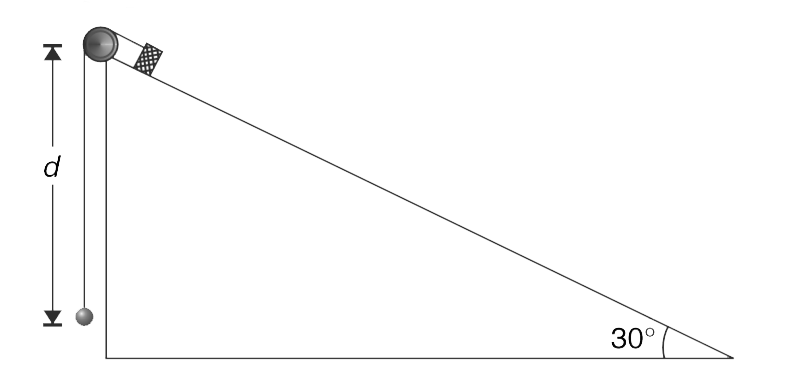 05:14View Solution
05:14View SolutionA uniform chain of mass M = 4.8 kg hangs in vertical plane as shown in the fig.
(a) Show that horizontal component of tension is same throughout the chain.
(b) Find tension in the chain at point P where the chain makes an angle `theta = 15^(@)` with horizontal.
(c) Find mass of segment AP of the chain.
[Take `g = 10 m//s^(2), "cos" 15^(@) = 0.96 , "sin"15^(@) = 0.25`]
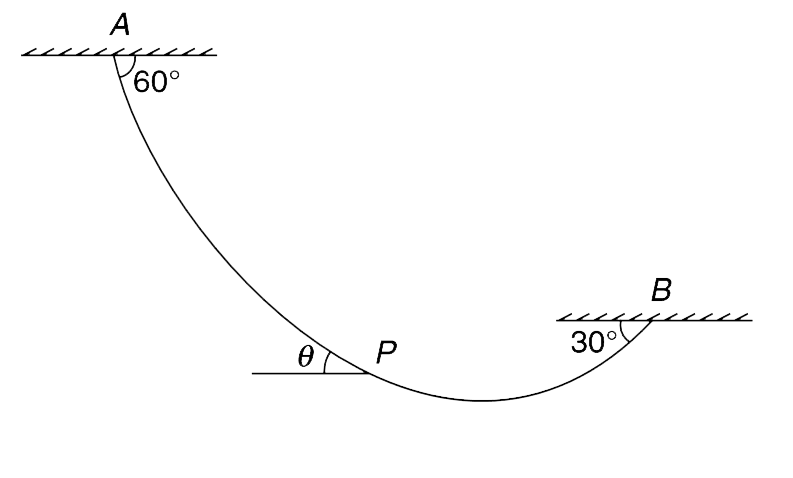 07:56View Solution
07:56View SolutionBlock A of mass M is placed on an incline plane, connected to a string, passing over a pulley as shown in the fig. The other end of the string also carries a block B of mass M. The system is held in the position shown such that triangle APQ lies in a vertical plane with horizontal line AQ in the plane of the incline surface.
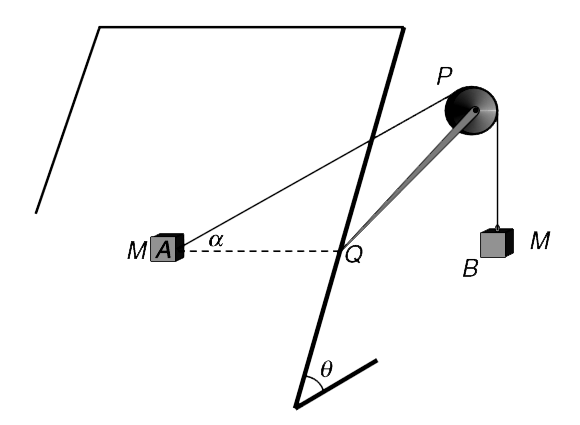
Find the minimum coefficient of friction between the incline surface and block A such that the system remains at rest after it is released. Take `theta = alpha = 45^(@)`04:36View SolutionFigure shown a fixed surface inclined at an angle `theta` to the horizontal. A smooth groove is cut on the incline along QR forming an angle `phi` with PR. A small block is released at point Q and it slides down to R in time t. Find t.
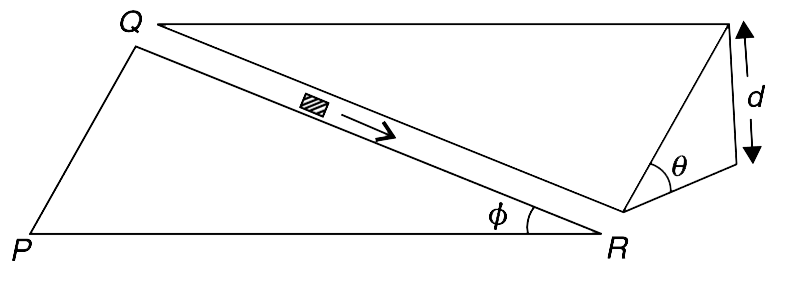 03:48View Solution
03:48View SolutionIn the system shown in the figure AB and CD are identical elastic cords having force constant K. The string connected to the block of mass M is inextensible and massless. The pulley is also massless. Initially, the cords are just taut. The end D of the cord CD is gradually moved up. Find the vertical displacement of the end D by the time the block leaves the ground.
 03:49View Solution
03:49View SolutionBlocks A and B have dimensions as shown in the fig. and their masses are 8 kg and 1 kg respectively. A small block C of mass 0.5 kg is placed on the top left corner of block A. All surfaces are smooth. A horizontal force F = 18 N is applied to the block B at time t = 0. At what time will the block C hit the ground surface? Take `g = 10 m//s^(2)`.
 04:50View Solution
04:50View SolutionThree identical smooth balls are placed between two vertical walls as shown in fig. Mass of each ball is m and radius is ` r = (5R)/(9)` where 2R is separation between the walls .
(a) Force between which two contact surface is maximum? Find its value.
(b) Force between which two contact surface is minimum and what is its value?
 08:43View Solution
08:43View SolutionA horizontal wooden block has a fixed rod OA standing on it. From top point A of the rod, two wires have been fixed to points B and C on the block. The plane of triangle OAB is perpendicular to the plane of the triangle OAC. There are two identical beads on the two wires. One of the wires is perfectly smooth while the other is rough. The wooden block is moved with a horizontal acceleration (a) that is perpendicular to the line OB and it is observed that both the beads do not slide on the wire. Find the minimum coefficient of friction between the rough wire and the bead.
 05:50View Solution
05:50View SolutionIn the arrangement shown in the fig. the pulley, the spring and the thread are ideal. The spring is stretched and the two blocks are in contact with a horizontal platform P. When the platform is gradually moved up by 2 cm the tension in the string becomes zero. If the platform is gradually moved down by 2 cm from its original position one of the blocks lose contact with the platform. Given M = 4 kg, m = 2 kg.
(a) Find the force constant (k) of the spring
(b) If the platform continues to move down after one of the blocks loses contact, will the other block also lose contact? Assume that that the platform moves very slowly.
 04:48View Solution
04:48View SolutionIn the arrangement shown in the fig. a monkey of mass M keeps itself as well as block A at rest by firmly holding the rope. Rope is massless and the pulley is ideal. Height of the monkey and block A from the floor is h and 2h respectively [h = 2.5 m]
(a) The monkey loosens its grip on the rope and slides down to the floor. At what height from the ground is block A at the instant the money hits the ground?
(b) Another block of mass equal to that of A is stuck to the block A and the system is released. The monkey decides to keep itself at height h above the ground and it allows the rope to slide through its hand. With what speed will the block strike the ground?
(c) In the situation described in (b), the monkey decides to prevent the block from striking the floor. The monkey remains at height h till the block crosses it. At the instant the block is crossing the monkey it begins climbing up the rope. Find the minimum acceleration of the monkey relative to the rope, so that the block is not able to hit the floor. Do you think that a monkey can climb with such an acceleration? (`g = 10ms^(-2)`)
 08:26View Solution
08:26View SolutionAn ideal spring is in its natural length (L) with two objects A and B connected to its ends. A point P on the unstretched spring is at a distance `(2L)/(3)` from B. Now the objects A and B are moved by 4 cm to the left and 8 cm to the right respectively. Find the displacement of point P.
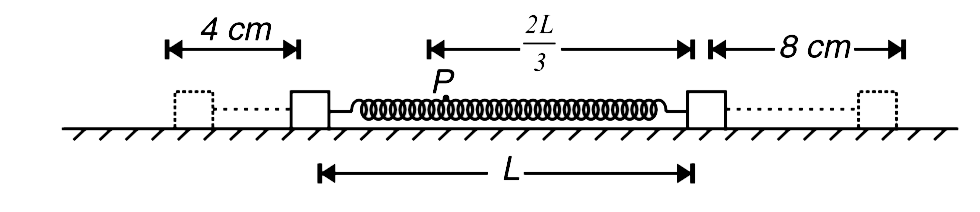 03:17View Solution
03:17View SolutionThe fig. shows an infinite tower of identical springs each having force constant k. The connecting bars and all springs are massless. All springs are relaxed and the bottom row of springs is fixed to horizontal ground. The free end of the top spring is pulled up with a constant force F. In equilibrium, find
(a) The displacement of free end A of the top spring from relaxed position.
(b) The displacement of the top bar B1 from the initial relaxed position.
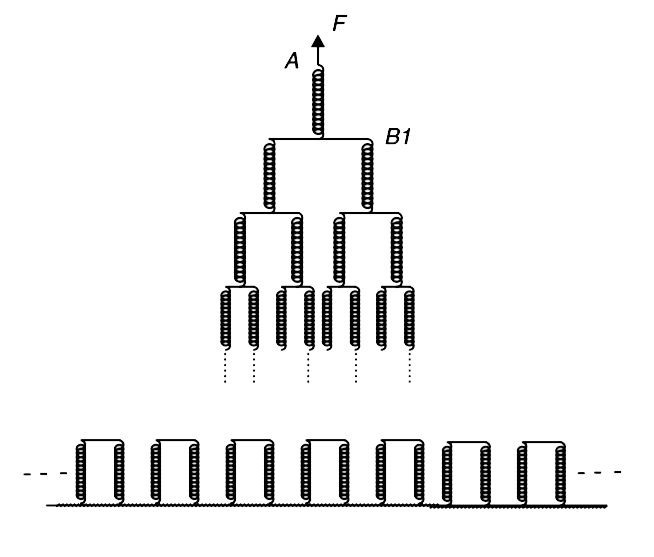 03:08View Solution
03:08View SolutionIn the system shown in the fig. there is no friction and string is light. Mass of movable pulley `P_(2) "is" M_(2)`. If pulley `P_(1)` is massless, what should be value of applied force F to keep the system in equilibrium?
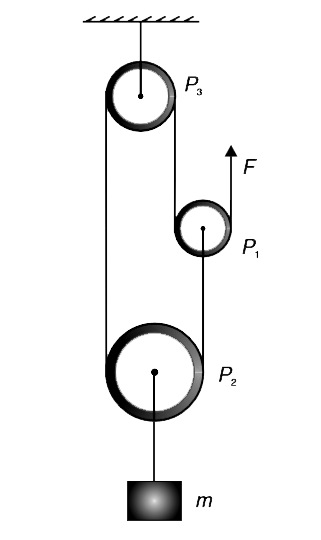 01:30View Solution
01:30View SolutionIn the system shown in the fig., the bead of mass m can slide on the string. There is friction between the bead and the string. Block has mass equal to twice that of the bead. The system is released from rest with length l of the string hanging below the bead. Calculate the distance moved by the block before the bead slips out of the thread. Assume the string and pulley to be massless.
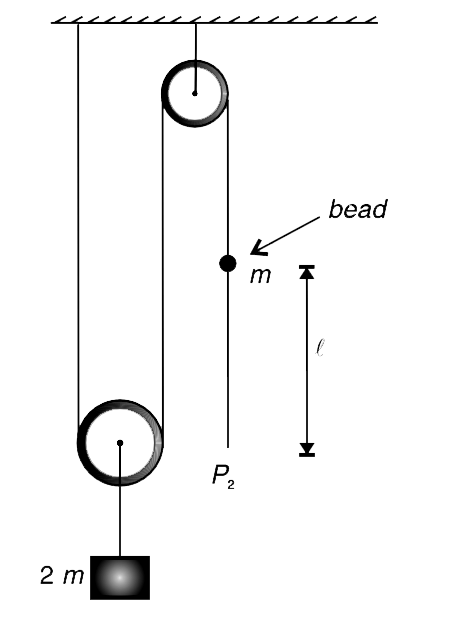 04:40View Solution
04:40View SolutionIn the arrangement shown in the fig. all pulleys are mass less and the strings are inextensible and light. Block A has mass M.
(a) If the system stays at rest after it is released, find the mass of the block B.
(b) If mass of the block B is twice the value found in part (a) of the problem, calculate the acceleration of block A.
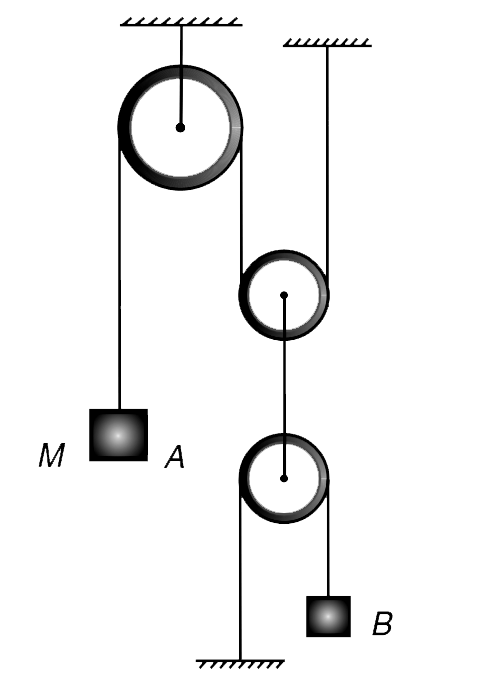 04:35View Solution
04:35View SolutionIn the fig. shown, the pulley and string are mass less and the incline is frictionless. The segment AP of the string is parallel to the incline and the segment PB is perpendicular to the incline. End of the string is pulled with a constant force F.
(a) If the block is moving up the incline with acceleration while being in contact with the incline , then angle `theta` must be less than `theta_(0)`. Find `theta_(0)`
If `theta = (theta_(0))/(2)` find the maximum acceleration with which the block can move up the plane without losing contact with the incline.
 04:54View Solution
04:54View SolutionA triangular wedge A is held fixed and a block B is released on its inclined surface, from the top. Block B reaches the horizontal ground in time t. In another experiment, the wedge A was free to slide on the horizontal surface and it took t’ time for the block B to reach the ground surface after it was released from the top. Neglect friction and assume that B remains in contact with A.
(a) Which time is larger t or t´? Tell by simple observation.
(b) When wedge A was free to move, it was observed that it moved leftward with an acceleration `(g)/(4)` and one of the two measured times (t & t´) was twice the other. Find the inclination `theta` of the inclined surface of the wedge.
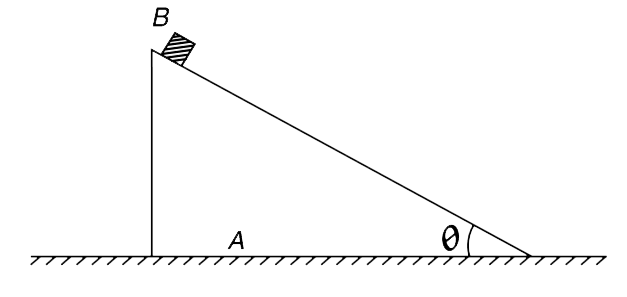 05:47View Solution
05:47View SolutionA block A is made to move up an inclined plane of inclination`theta` with constant acceleration `a_(0)` as shown in figure. Bob B, hanging from block A by a light inextensible string, is held vertical and is moving along with the block. Calculate the magnitude of acceleration of block A relative to the bob immediately after bob is released.
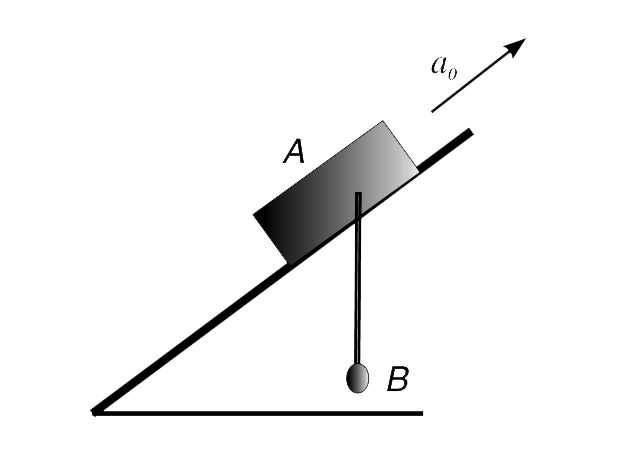 02:03View Solution
02:03View SolutionA 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
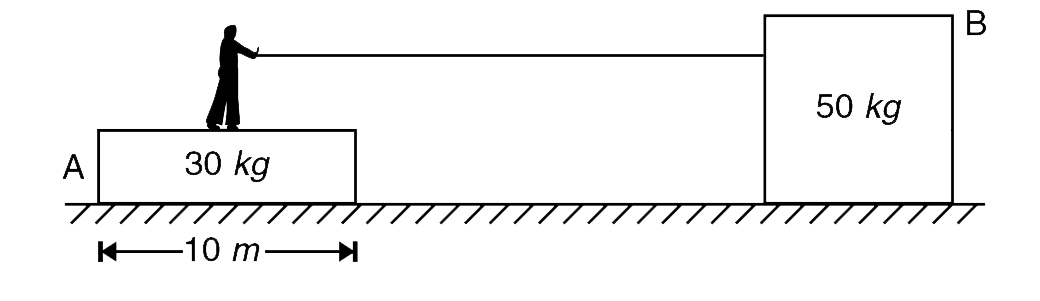 05:10View Solution
05:10View SolutionA wedge is placed on the smooth surface of a fixed incline having inclination `theta` with the horizontal. The vertical wall of the wedge has height h and there is a small block A on the edge of the horizontal surface of the wedge. Mass of the wedge and the small block are M and m respectively.
(a) Find the acceleration of the wedge if friction between block A and the wedge is large enough to prevent slipping between the two.
(b) Find friction force between the block and the wedge in the above case. Also find the normal force between the two.
(c) Assuming there is no friction between the block and the wedge, calculate the time in which the block will hit the incline.
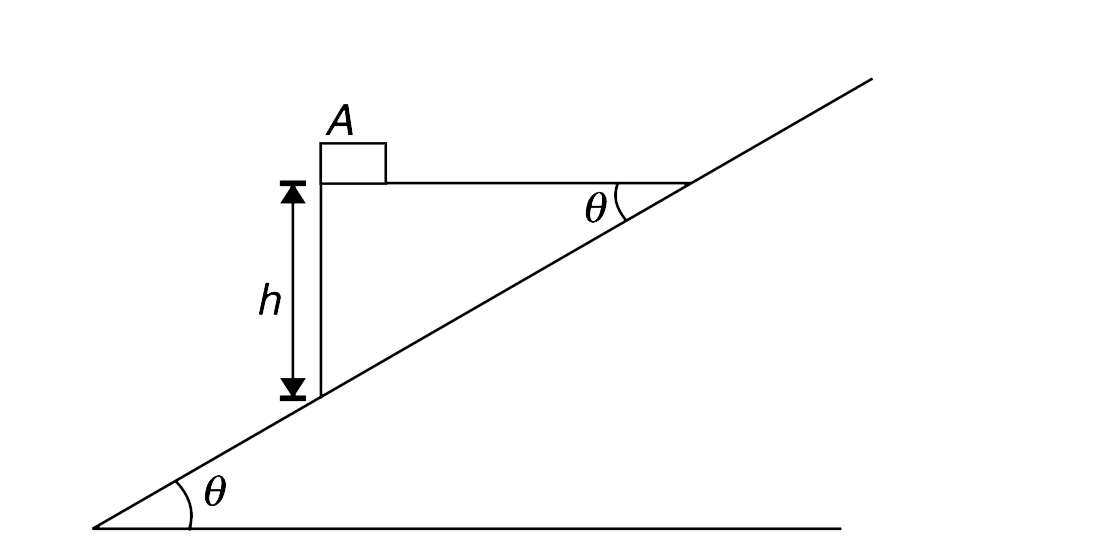 09:22View Solution
09:22View SolutionIn the system shown in figure, all surfaces are smooth, pulley and strings are massless. Mass of both A and B are equal. The system is released from rest.

(a) Find the `veca_(A). veca_(B)` immediately after the system is released. `veca_(A) "and" veca_(B)` are accelerations of block A and B respectively.
(b) Find `veca_(A)` immediately after the system is released.03:15View SolutionA block is placed on an incline having inclination `theta` . There is a rigid L shaped frame fixed to the block. A plumb line (a ball connected to a thread) is attached to the end A of the frame. The system is released on the inline. Find the angle that the plumb line will make with vertical in its equilibrium position relative to the block when
(a) the incline is smooth
(b) there is friction and the acceleration of the block is half its value when the incline is smooth
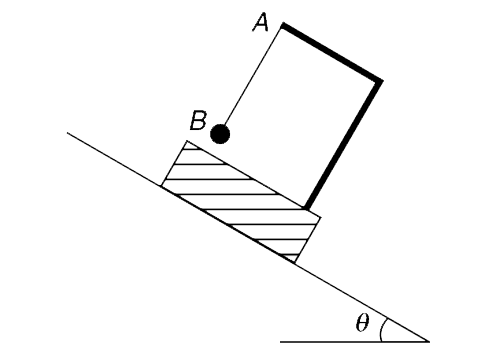 08:09View Solution
08:09View SolutionA wedge of mass m is placed on a horizontal smooth table. A block of mass m is placed at the mid point of the smooth inclined surface having length L along its line of greatest slope. Inclination of the inclined surface is `theta= 45^(@)`. The block is released and simultaneously a constant horizontal force F is applied on the wedge as shown.
(a) What is value of F if the block does not slide on the wedge?
(b) In how much time the block will come out of the incline surface if applied force is 1.5 times that found in part (a)
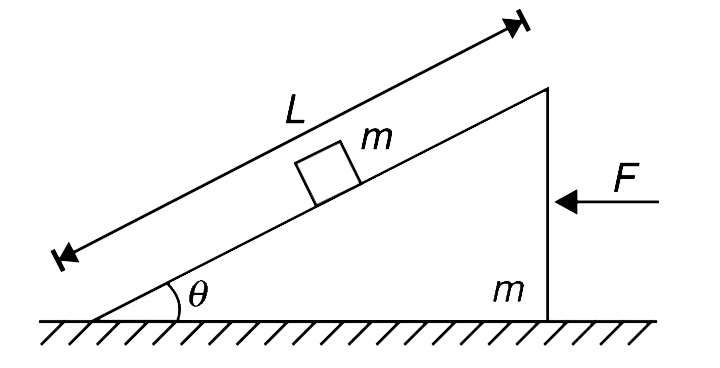 11:22View Solution
11:22View SolutionA rod is kept inclined at an angle `theta` with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is `mu`, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
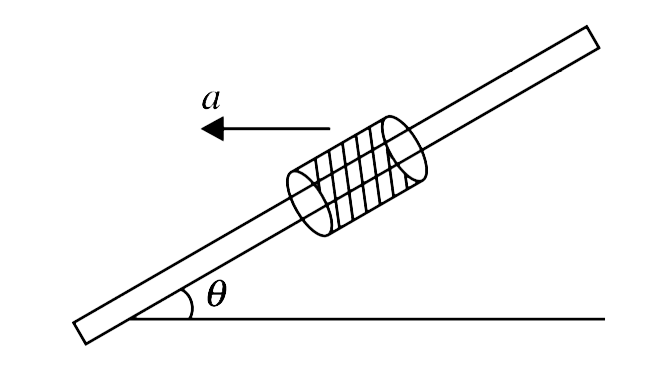 07:43View Solution
07:43View SolutionIn the arrangement shown in figure, a block A of mass m has been placed on a smooth wedge B of mass M. The wedge lies on a horizontal smooth surface. Another block C of mass `(M)/(4)` has been placed in contact with the wedge B as shown. The coefficient of friction between the block C and the vertical wedge wall is `mu= (3)/(4)`. Find the ratio `(m)/(M)` for which the block C will not slide with respect to the wedge after the system is released?
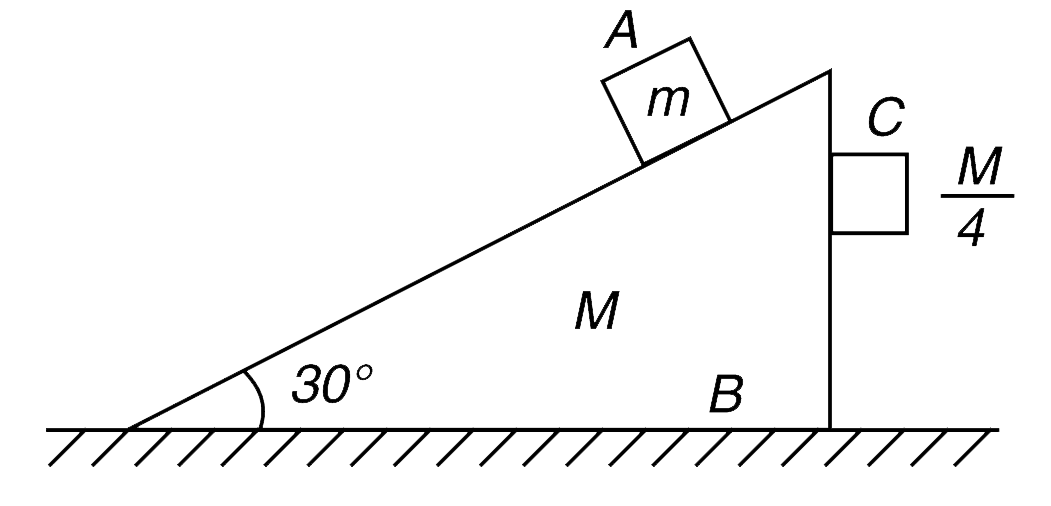 10:06View Solution
10:06View SolutionA smooth rod is fixed at an angle `alpha` to the horizontal. A small ring of mass m can slide along the rod. A thread carrying a small sphere of mass M is attached to the ring. To keep the system in equilibrium, another thread is attached to the ring which carries a load of mass `m_(0)`at its end (see figure). The thread runs parallel to the rod between the ring and the pulley. All threads and pulley are massless.
(a) Find `m_(0)` so that system is in equilibrium.
(b) Find acceleration of the sphere M immediately after the thread supporting `m_(0)` is cut.
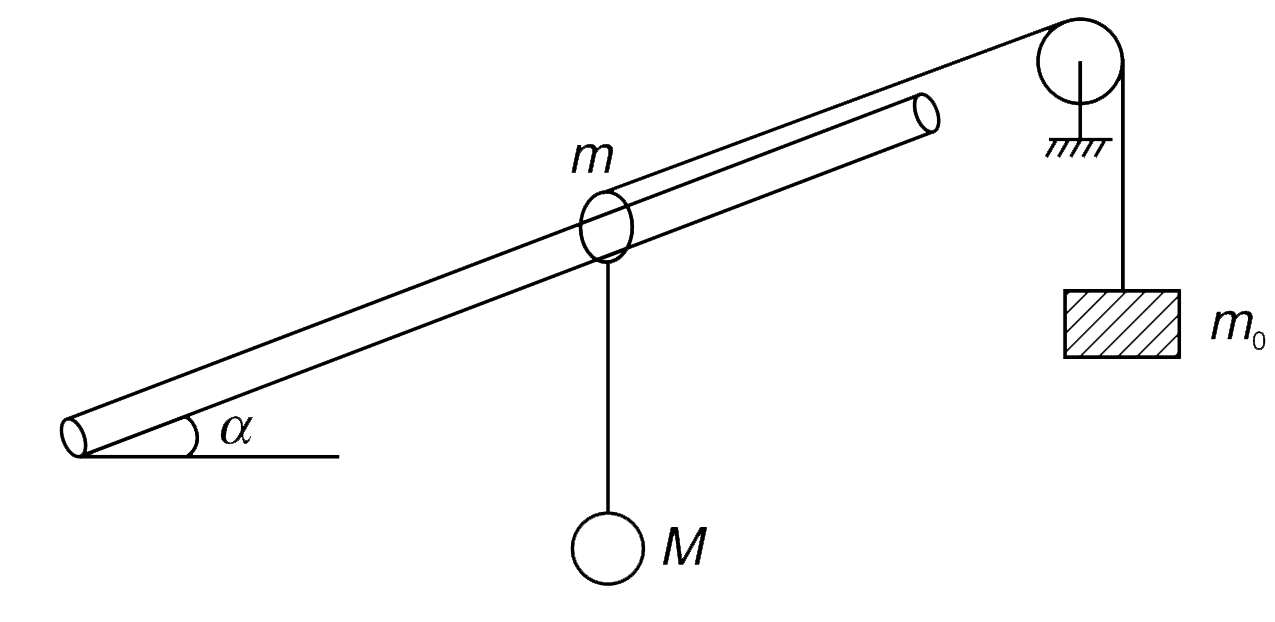 05:38View Solution
05:38View SolutionIn the system shown in figure all surfaces are smooth and string and pulleys are light. Angle of wedge`theta = sin^(-1) ((3)/(5))`. When released from rest it was found that the wedge of mass `m_(0)` does not move . Find `(M)/(m)`.
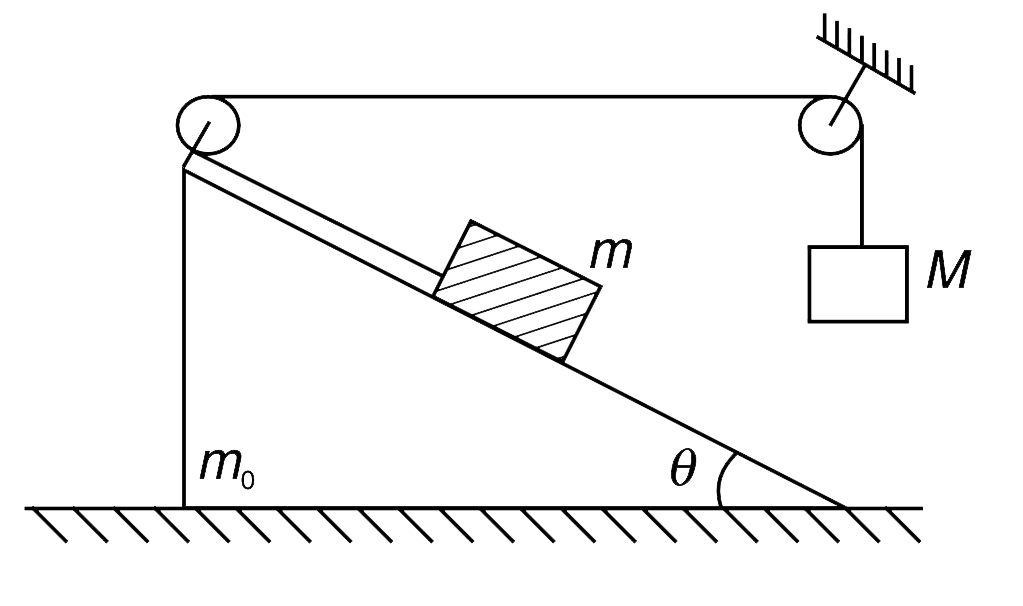 06:40View Solution
06:40View SolutionIn the system shown in figure, the two springs `S_(1) "and" S_(2)` have force constant k each. Pulley, springs and strings are all massless. Initially, the system is in equilibrium with spring `S_(1)` stretched and `S_(2)` relaxed. The end A of the string is pulled down slowly through a distance L. By what distance does the block of mass M move?
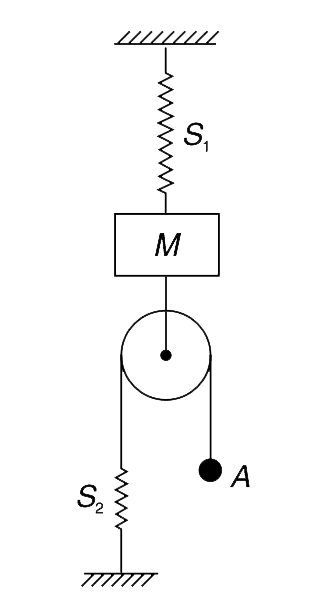 03:24View Solution
03:24View SolutionA block of mass m = 1 kg is kept pressed against a spring on a rough horizontal surface. The spring is compressed by 10 cm from its natural length and to keep the block at rest in this position a horizontal force (F) towards left is applied. It was found that the block can be kept at rest if `8 Nle F le 18 N`. Find the spring constant (k) and the coefficient of friction `(mu)` between the block and the horizontal surface.
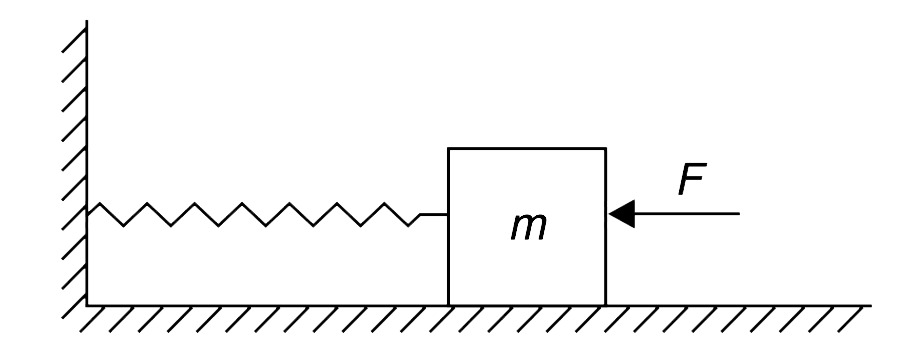 03:23View Solution
03:23View SolutionAn experimenter is inside a uniformly accelerated train. Train is moving horizontally with constant acceleration `a_(0)`. He places a wooden plank AB in horizontal position with end A pointing towards the engine of the train. A block is released at end A of the plank and it reaches end B in time `t_(1)`. The same plank is placed at an inclination of `45^(@)` to the horizontal. When the block is released at A it now climbs to B in time`t_(2)`. It was found that `(t_(2))/(t_(1))= 2^((5)/(4))`. What is the coefficient of friction between the block and the plank?
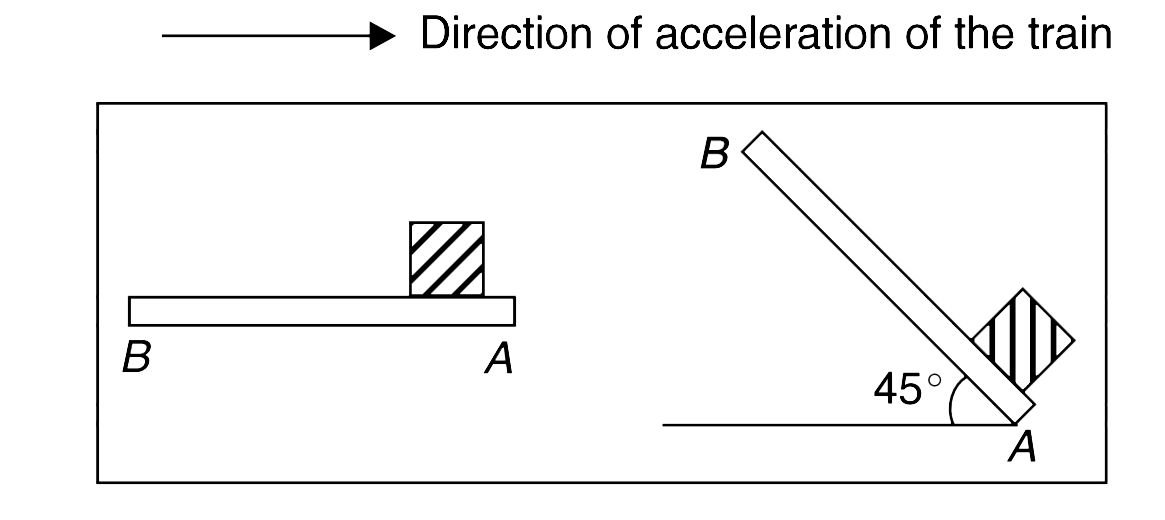 06:12View Solution
06:12View SolutionTwo hemispheres of radii `R` and `r(lt R)` are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is `mu`. Then the maximum value of the ratio `(r)/(R)` for which the rod will not slide is :
 07:08View Solution
07:08View SolutionIn order to lift a heavy block A, an engineer has designed a wedge system as shown. Wedge C is fixed. A horizontal force F is applied to B to lift block A. Wedge B itself has negligible mass and mass of A is M. The coefficient of friction at all surfaces is `mu`. Find the value of applied force F at which the block A just begins to rise.
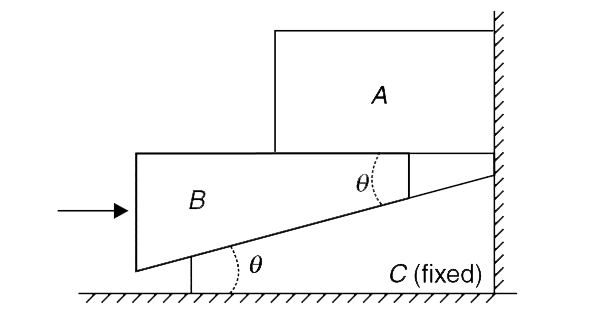 03:54View Solution
03:54View SolutionA 60 kg platform has been placed on a rough incline having inclination `theta = 37^(@)`. The coefficient of friction between the platform and the incline is `mu = 0.5`. A 40 kg man is running down on the platform so as to keep the platform stationary. What is the acceleration of the man? It is known that the man cannot manage to go beyond an acceleration of `7m//s^(2).["sin"37^(@) = (3)/(5)]`
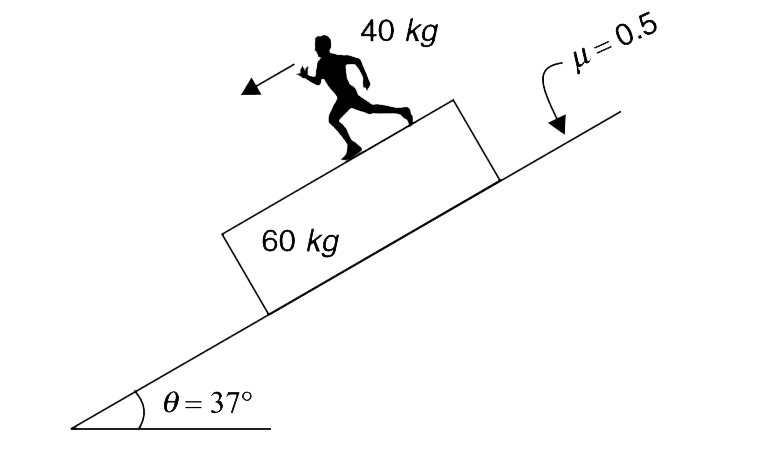 04:33View Solution
04:33View SolutionIn the system show in figure, mass of the block placed on horizontal surface is M = 4 kg. A constant horizontal force of F = 40 N is applied on it as shown. The coefficient of friction between the blocks and surfaces is `mu = 0.5`. Calculate the values of mass m of the block on the incline for which the system does not move . `["sin" 37^(@) = (3)/(5), g = 10 m//s^(2)]`
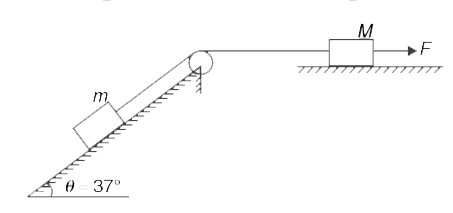 05:02View Solution
05:02View SolutionIn the arrangement shown in the figure, block A of mass 8 kg rests on a horizontal table having coefficient of friction `mu = 0.5`. Block B has a mass of 6 kg and rests on a smooth incline having inclination angle `theta = sin^(-1) ((2)/(5))` . All pulleys and strings are mass less . Mass of block C is M .
`[g = 10 m//s^(2)]`

(a) Find value of M for which block B does not accelerate
(b) Find maximum value of M for which A does not accelerate.05:49View SolutionIn the arrangement shown in figure, pulley and string are light. Friction coefficient between the two blocks is `mu` whereas the incline is smooth. Block A has mass m and difference in mass of the two blocks is`deltam`. Find minimum value of m for which the system will not accelerate when released from rest.
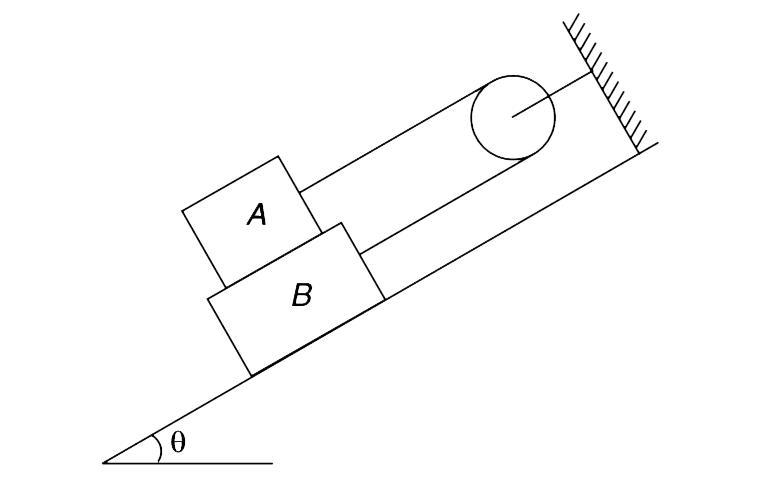 03:38View Solution
03:38View SolutionIn the arrangement shown in figure pulley P can move whereas other two pulleys are fixed. All of them are light. String is light and inextensible. The coefficient of friction between 2 kg and 3 kg block is `mu = 0.75` and that between 3 kg block and the table is `mu = 0.5`. The system is released from rest

(i) Find maximum value of mass M, so that the system does not move. Find friction force between 2 kg and 3 kg blocks in this case.
(ii) If M = 4 kg, find the tension in the string attached to 2 kg block.
(iii) If M = 4 kg and `mu_(1) = 0.9`, find friction force between the two blocks, and acceleration of M.
(iv) Find acceleration of M if `m_(1) = 0.75, m_(2) = -0.9` and M = 4 kg.06:22View SolutionA rope of length `((pi)/(2) + 1)` R has been placed on a smooth sphere of radius R as shown in figure. End A of the rope is at the top of the sphere and end B is overhanging. Mass per unit length of the rope is `lambda` . The horizontal string holding this rope in place can tolerate tension equal to weight of the rope. Find the maximum mass `(M_(0))` of a block that can be tied to the end B of the rope so that the string does not break.
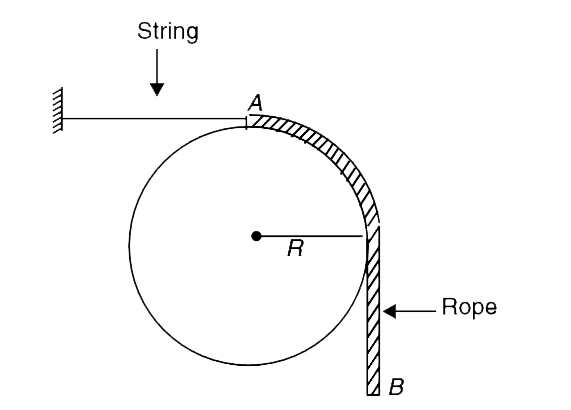 02:30View Solution
02:30View SolutionA uniform rope has been placed on a sloping surface as shown in the figure. The vertical separation and horizontal separation between the end points of the rope are H and X respectively. The friction coefficient `(mu)` is just good enough to prevent the rope from sliding down. Find the value of `mu`.
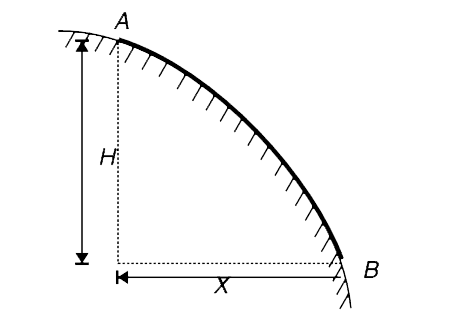 03:31View Solution
03:31View SolutionA uniform rope ABCDE has mass M and it is laid along two incline surfaces (AB and CD) and two horizontal surfaces (BC and DE) as shown in figure. The four parts of the rope AB, BC, CD and DE are of equal lengths. The coefficient of friction `(mu)` is uniform along the entire surface and is just good enough to prevent the rope from sliding.

(a) Find `mu`
(b) x is distance measured along the length of the rope starting from point A. Plot the variation of tension in the rope (T) with distance x.
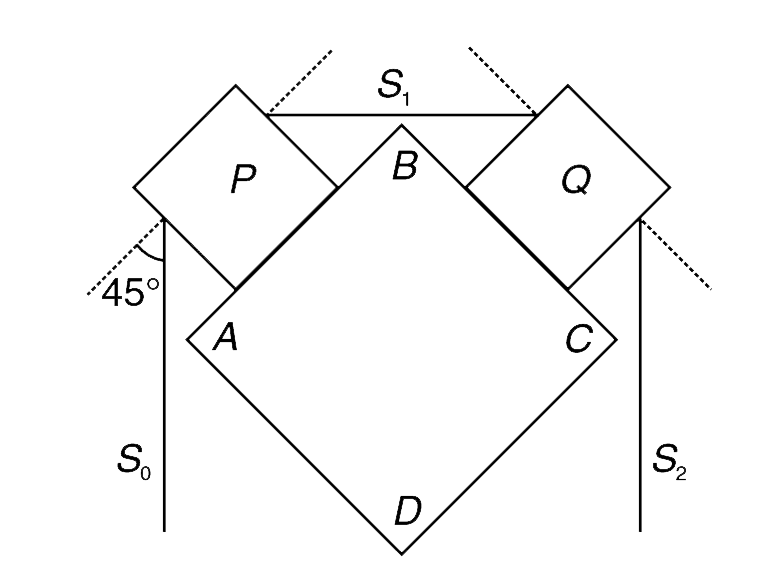
(c) Find the maximum tension in the rope.07:53View Solution(i) Four small blocks are interconnected with light strings and placed over a fixed sphere as shown. Blocks A, B and C are identical each having mass m = 1 kg. Block D has a mass of m´ = 2 kg. The coefficient of friction between the blocks and the sphere is `mu = 0.5`. The system is released from the position shown in figure.

(a) Find the tension in each string. Which string has largest tension?
(b) Find the friction force acting on each block.
[Take `"tan"37^(@) = (3)/(4) , g = 10 m//s^(2)`]
(ii) A fixed square prism ABCD has its axis horizontal and perpendicular to the plane of the figure. The face AB makes `45^(@)` with the vertical. On the upper faces AB and BC of the prism there are light bodies P and Q respectively. The two bodies (P and Q) are connected using a string `S_(1)` and strings `S_(0)` and `S_(2)` are hanging from P and Q respectively. All strings are mass less, and inextensible. String` S_(1)` is horizontal and the other two strings are vertical. The coefficient of friction between the bodies and the prism is `mu_(0)` . Assume that P and Q always remain in contact with the prism.
(a) If tension in `S_(0)` is `T_(0)`, find the minimum tension `(T_(1))` in `S_(1)` to keep the body P at rest.
(b) A mass `M_(0)` is tied to the lower end of string `S_(0)` and another mass `m_(2)` is tied to `S_(2)` . Find the minimum value of m2 so as to keep P and Q at rest.
 05:49View Solution
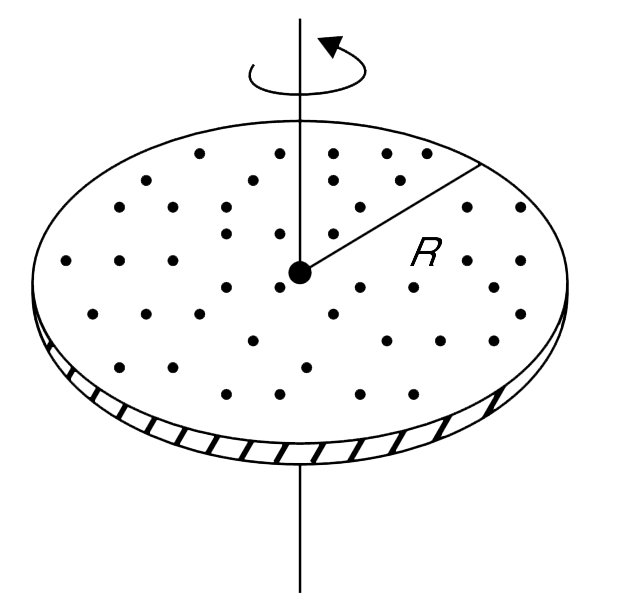
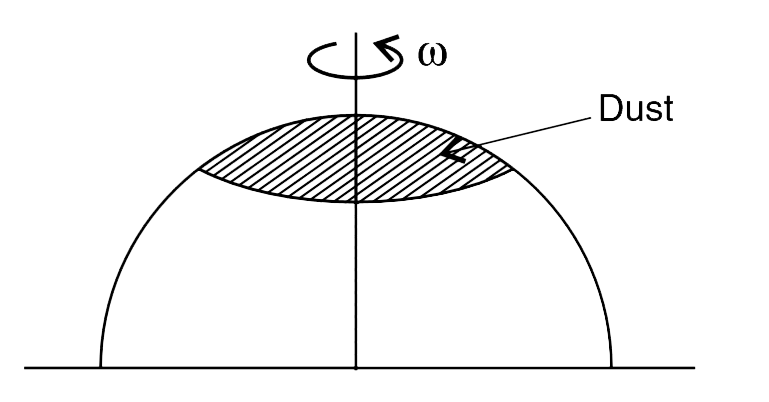
05:49View SolutionA metal disc of radius R can rotate about the vertical axis passing through its centre. The top surface of the disc is uniformly covered with dust particles. The disc is rotated with gradually increasing speed. At what value of the angular speed `(omega)` of the disc the `75% `of the top surface will become dust free. Assume that the coefficient of friction between the dust particles and the metal disc is `mu = 0.5`. Assume no interaction amongst the dust particles.
 03:02View Solution
03:02View SolutionA sphere of mass M is held at rest on a horizontal floor. One end of a light string is fixed at a point that is vertically above the centre of the sphere. The other end of the string is connected to a small particle of mass m that rests on the sphere. The string makes an angle `alpha = 30^(@)` with the vertical. Find the acceleration of the sphere immediately after it is released. There is no friction anywhere.
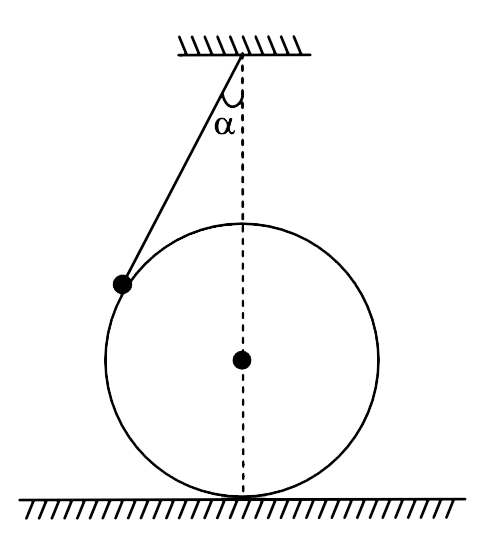 03:35View Solution
03:35View SolutionA light rod AB is fitted with a small sleeve of mass m which can slide smoothly over it. The sleeve is connected to the two ends of the rod using two springs of force constant 2k and k (see fig). The ends of the springs at A and B are fixed and the other ends (connected to sleeve) can move along with the sleeve. The natural length of spring connected to A is `l_(0)`. Now the rod is rotated with angular velocity w about an axis passing through end A that is perpendicular to the rod. Take `(k)/(momega^(2)) = eta` and express the change in length of each spring (in equilibrium position of the sleeve relative to the rod) in terms of `l_(0)` and `eta`.
 02:18View Solution
02:18View SolutionA metallic hemisphere is having dust on its surface. The sphere is rotated about a vertical axis passing through its centre at angular speed `omega = 10 "rad" s^( –1)`. Now the dust is visible only on top `20%` area of the curved hemispherical surface. Radius of the hemisphere is R = 0.1 m. Find the coefficient of friction between the dust particle and the hemisphere [`g = 10 ms^(–2)`].
 04:02View Solution
04:02View SolutionCivil engineers bank a road to help a car negotiate a curve. While designing a road they usually ignore friction. However, a young engineer decided to include friction in his calculation while designing a road. The radius of curvature of the road is R and the coefficient of friction between the tire and the road is `mu`.
(a) What should be the banking angle `(theta_(0))` so that car travelling up to a maximum speed `V_(0)` can negotiate the curve.
(b) At what speed `(V_(1))` shall a car travel on a road banked at `theta_(0)` so that there is no tendency to skid. (No tendency to skid means there is no static friction force action on the car).
(c) The driver of a car travelling at speed `(V_(1))` starts retarding (by applying brakes). What angle (acute, obtuse or right angle) does the resultant friction force on the car make with the direction of motion?06:43View SolutionA turn of radius 100 m is banked for a speed of 20 m/s
(a) Find the banking angle
(b) If a vehicle of mass 500 kg negotiates the curve find the force of friction on it if its speed is – (i) 30 m/s (ii) 10 m/s
Assume that friction is sufficient to prevent skidding and slipping.
[Take `"tan" 22^(@) = 0.4 , "sin" 22^(@) = 0.375 , "cos" 22^(@) = 0.93 , g = 10 ms^(-2)`]06:25View SolutionA horizontal circular turning has a curved length L and radius R. A car enters the turn with a speed `V_(0)` and its speed increases at a constant rate f. If the coefficient of friction is `mu`,
(a) At what time `t_(0)`, after entering the curve, will the car skid? (Take it for granted that it skids somewhere on the turning)
(b) At a time `t (lt t_(0))` what is the force of friction acting on the car?05:45View SolutionA 70 kg man enters a lift and stands an a weighing scale inside it. At time t = 0, the lift starts moving up and stops at a higher floor at t = 9.0 s. During the course of this journey, the weighing scale records his weight and given a plot of his weight vs time. The plot is shown in the fig. [Take `g = 10 m//s^(2)`]
(a) Find `F_(0)`
(b) Find the magnitude of maximum acceleration of the lift.
(c) Find maximum speed acquired by the lift.
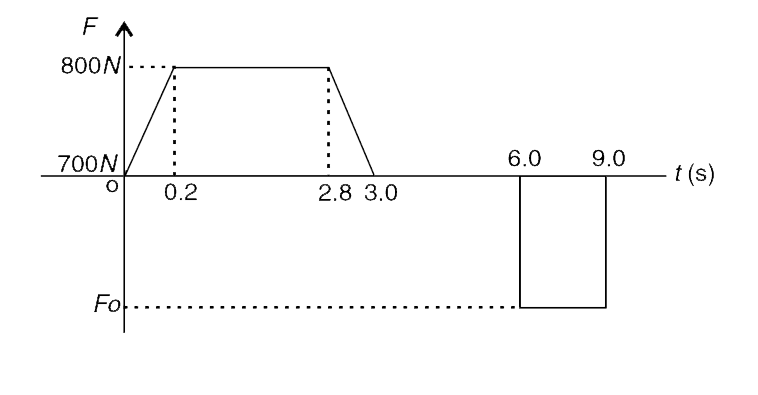 03:29View Solution
03:29View SolutionThree small discs are connected with two identical massless rods as shown in fig. The rods are pinned to the discs such that angle between them can change freely. The system is placed on a smooth horizontal surface with discs A and B touching a smooth wall and the angle ACB being `90^(@)`. A force F is applied to the disc C in a direction perpendicular to the wall. Find acceleration of disc B immediately after the force starts to act. Masses of discs are `m_(A) = m , m_(B) = 2 m , m_(C) = m `[ wall is perpendicular to the plane of the fig.]
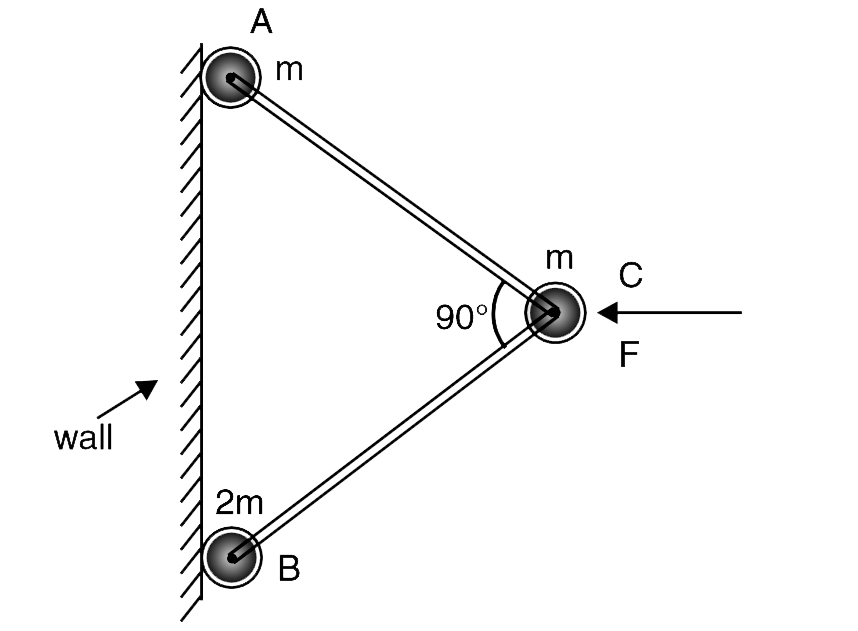 04:56View Solution
04:56View SolutionFigure shows two blocks in contact sliding down an inclined surface of inclination 30º. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and the incline is μ2. Calculate the acceleration of the 2.0 kg block if μ1 = 0.30 and μ2 = 0.20, Take g = 10 m/s2
 07:57View Solution
07:57View SolutionA small collar of mass m = 100 g slides over the surface of a horizontal circular rod of radius R = 0.3 m. The coefficient of friction between the rod and the collar is `mu = 0.8`. Find the angle made with vertical by the force applied by the rod on the collar when speed of the collar is V = 2 m/s.
 02:50View Solution
02:50View SolutionA flat race track consists of two straight section AC and DB each of length 180 m and one semi circular section DC of radius R = 150 m. A car starting from rest at A has to reach B in least possible time (the car may cross through point B and need not stop there). The coefficient of friction between the tyres and the road is `mu = 0.6` and the top speed that the car can acquire is 180 kph. Find the minimum time needed to move from A to B under ideal conditions. Braking is not allowed in the entire journey [`g = 10 m//s^(2)`]
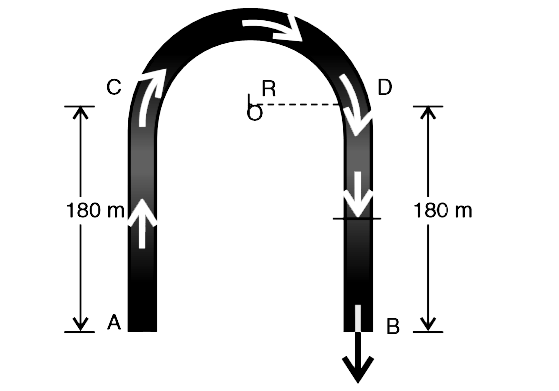 05:37View Solution
05:37View SolutionA small insect is climbing slowly along the inner wall of a hemispherical bowl of radius R. The insect is unable to climb beyond `theta = 45^(@)`. Whenever it tries to climb beyond `theta = 45^(@)`, it slips.
(a) Find the minimum angular speed `omega` with which the bowl shall be rotated about its vertical radius so that the insect can climb upto `theta = 60^(@)`.
(b) Find minimum `omega` for which the insect can move out of the bowl.
 06:01View Solution
06:01View Solution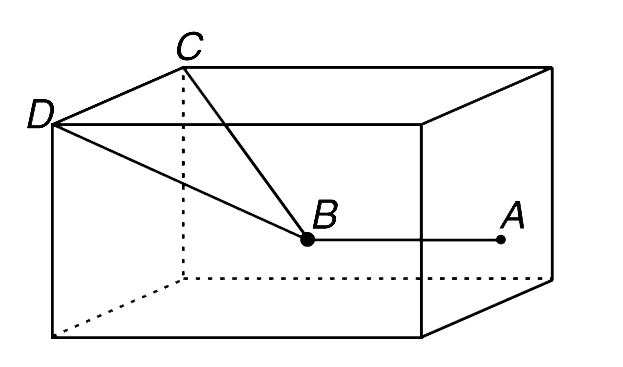
A room is in shape of a cube . A heavy ball (B) is suspended at the centre of the room tied to three inextensible strings as shown. String BA is horizontal with A being the centre point of the wall. Find the ratio of tension in the string BA and BC.03:33View SolutionTwo identical smooth disc of radius R have been placed on a frictionless table touching each other. Another circular plate is placed between them as shown in figure. The mass per unit area of each object is `sigma`, and the line joining the centers of the plate and the disc is `theta`
(a) Find the minimum horizontal force `F_(0)` that must be applied to the two discs to keep them together.
(b) Angle `theta` can be changed by changing the size of the circular plate. Find `F_(0)` when `theta rarr 0`.
[use `"cos"theta = 1 - (theta^(2))/(2)` and `"sin"theta = theta "for small" theta`]
(c) Find `F_(0)` when `theta rarr (pi)/(2)` . Explain the result .
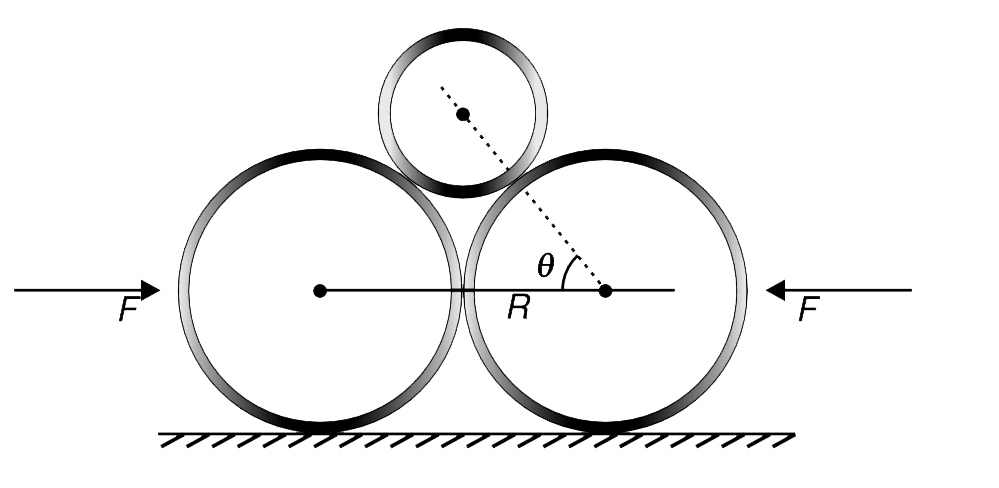 05:57View Solution
05:57View SolutionThree identical smooth cylinders, each of mass m and radius r are resting in equilibrium within a fixed smooth cylinder of radius R (only a part of this cylinder has been shown in the fig). Find the largest value of R in terms of r for the small cylinders to remain in equilibrium.
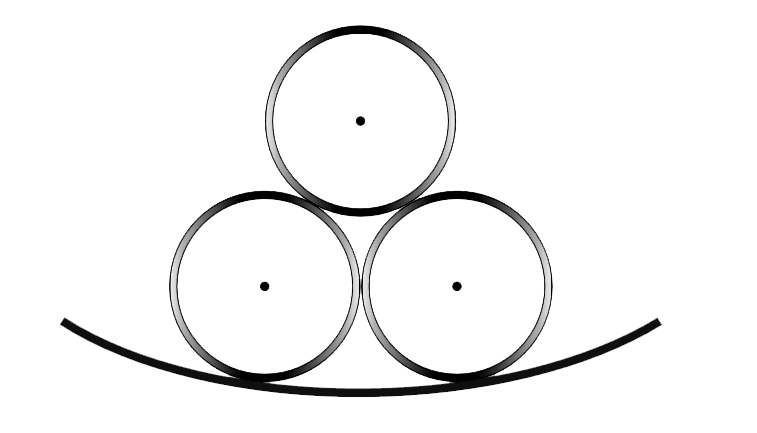 05:04View Solution
05:04View SolutionA massless spring of force constant K and natural length `l_(0)` is hanging from a ceiling. An insect of mass m is sitting at the lower end of the spring and the system is in equilibrium . The insect starts slowing climbing up the spring so as to eat a bug sitting on the ceiling. Assume that insect climbs without slipping on the spring and `K = (mg)/(l_(0))` . find the length of the spring when the insect is at `(1)/(4)th` of its original distance from the bug .
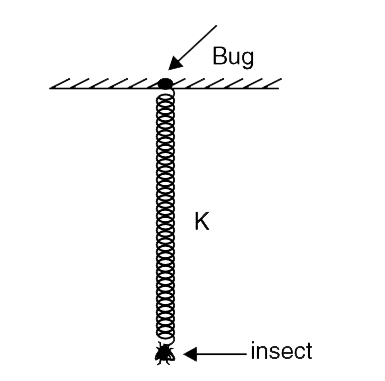 04:17View Solution
04:17View SolutionIn the system shown in fig., all pulleys are mass less and the string is inextensible and light.
(a) After the system is released, find the acceleration of mass `m_(1)`
(b) If `m_(1) = 1 kg, m_(2) = 2 kg "and" m_(3) = 3 `kg then what must be value of mass `m_(4)` so that it accelerates downwards?
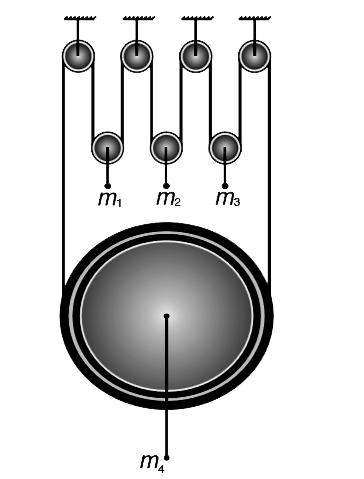 04:53View Solution
04:53View SolutionIn the system shown in fig., block A and C are placed on smooth floors and both have mass equal to `m_(1)`. Blocks B and D are identical having mass `m_(2)` each. Coefficient of friction
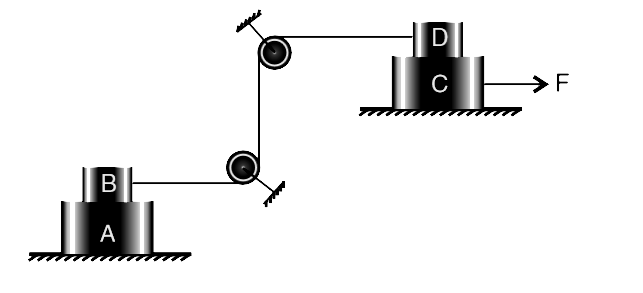
Between A and B and that between C and D are both equal to `mu`. String and pulleys are light. A horizontal force F is applied on block C and is gradually increased.
(a) Find the maximum value of F (call it `F_(0)`) so that all the four blocks move with same acceleration.
(b) Will the value of `F_(0)` increase or decrease if another block (E) of mass `m_(2)` is placed above block D and coefficient of friction between E and D is `mu`?02:27View SolutionA chain with uniform mass per unit length lies in a vertical plane along the slope of a smooth hill. The two end of the chain are at same height. If the chain is released from this position find its acceleration.
 03:17View Solution
03:17View SolutionA 4 kg block is placed on a rough horizontal surface. The coefficient of friction between the block and the surface is `mu= 0.5`. A force F = 18 N is applied on the block making an angle `theta` with the horizontal. Find the range of values of `theta` for which the block can start moving.
[Take `g = 10 m//s^(2) , tan^(-1)(2) = 63^(@) sin^(-1) ((10)/(9sqrt(1.25))) = 84^(@)`]
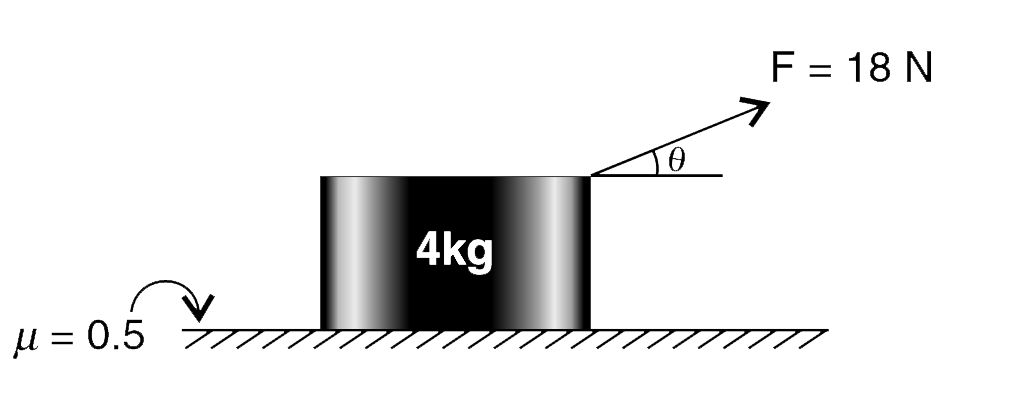 04:08View Solution
04:08View SolutionA rope of mass m is hung from a ceiling. The centre point is pulled down with a vertical force F. The tangent to the rope at its ends makes an angle `alpha` with horizontal ceiling. The two tangents at the lower point make an angle of `theta` with each other. Find `theta` .
 03:23View Solution
03:23View Solution
All Questions questions and complete solutions for chapter NEWTONS LAWS OF MOTION of ARIHANT PHYSICS (HINGLISH) of Class 11
