Complete Solutions to Heat Transfer of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| ARIHANT MASTER PROBLEM | Heat Transfer |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
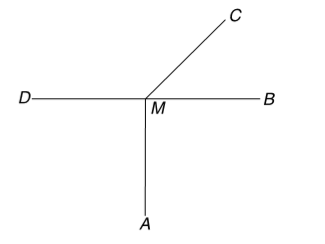
Four metal rods each of length L and cross sectional area A are joined at point M. Thermal conductivities of MA, MB and MD are equal and that of MC is thrice that of MA. The end points A, B, C and D are kept in large reservoirs. Heat folws into the junction from B at a rate of `P(Js^(-1))` and C from at a rate of 3P. Heat flows out of D at a rate of 5P.
(a) Find the relation between temperatures of points A, B and C.
(b) Find temperature of `D` if temperature of A and M and `T_(A)` and `T_(M)` respectively.
 05:03View Solution
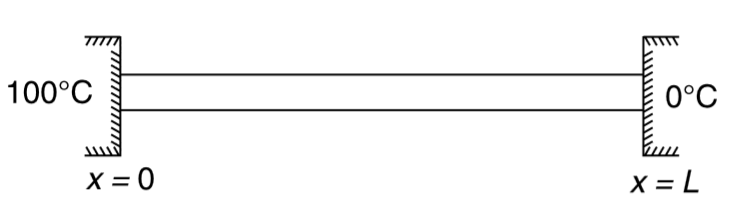
05:03View SolutionThe two ends of a uniform metallic rod are maintained at `100^(@)C` and `0^(@)C` as shown in the figure. Assume that end of the rod at `100^(@)C` is at x = 0 and the other end at `0^(@)C` is at x = L. Plot the variation of temperature as x changes from 0 to L in steady state. Consider two cases.
(a) The rod is perfectly lagged.
(b) The rod is not lagged and surrounding is at `0^(@)C`.
 03:47View Solution
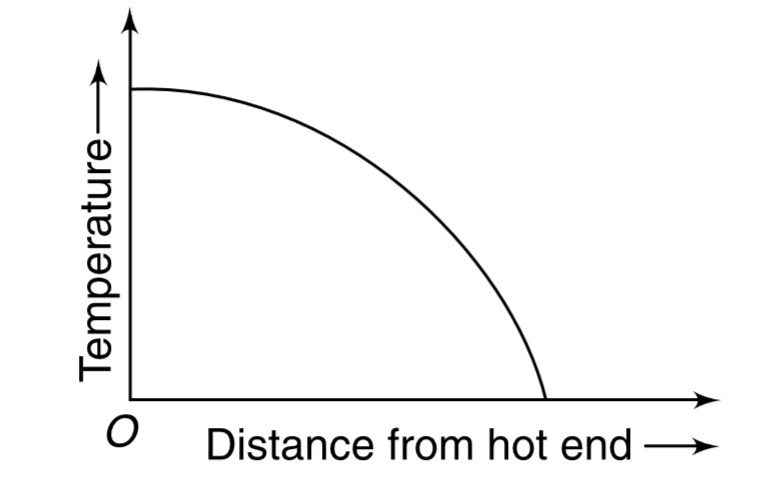
03:47View SolutionThe ends of a metallic bar are maintained at different temperature and there is no loss/gain of heat from the sides of the bar due to conduction or radiation. In the steady state the temperature variation along the length of the bar is a shown in the figure what do you think about the cross sectional area of the bar?
 02:22View Solution
02:22View SolutionA thick spherical shell of inner and outer radii r and R respectively has thermal conductivity `k = (rho)/(x^(n))` , where `rho` is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature `T_(1)` and `T_(2) (lt T_(1))`
(a) Find the value of number n (call it `n_(0)`) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For `n=n_(0)`, find the value of x at which the temperature is `(T_(1)+T_(2))/(2)`
(c) For `n = n_(0)`, calculate the rate of flow of heat through the shell.05:14View SolutionThree bars of aluminium, brass and copper are of equal length and cross section. The three pieces are joined together as shown in A, B and C and the ends are maintained at `100^(@)C` and `0^(@)C`. The thermal conductivities of aluminium, brass and copper are in ratio 2 : 1 : 4. Assume no heat loss through curved surface of the bar and that the system is in steady state.
(a) In which of the three cases (A, B or C) the temperature difference across aluminium bar will be maximum?
(b) Draw a graph showing variation of temperature from one end of the bar to another in case B. 07:07View Solution
07:07View SolutionA lake is covered with ice 5 cm thick and the atmospheric temperature above the ice is` – 10^(@)C`. At what rate (in cm/hour) will the ice layer thicken? Thermal conductivity of ice `= 0.005` cgs unit, density of ice `= 0.9 g//cc` and latent heat of fusion of ice = 80 cal/g.
03:52View SolutionA liquid having mass `m = 250` g is kept warm in a vessel by use of an electric heater. The liquid is maintained at `50^(@)C` when the power supplied by heater is 30 watt and surrounding temperature is `20^(@)C`. As the heater is switched off, the liquid starts cooling and it was observed that it took 10 second for temperature to fall down from `40^(@)C` to `39.9^(@)C`. Calculate the specific heat capacity of the liquid. Assume Newton’s law of cooling to be applicable.
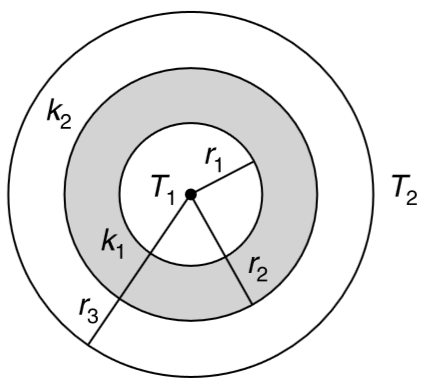
03:38View Solution(i) A cylindrical pipe of length L has inner and outer radii as a and b respectively. The inner surface of the pipe is at a temperature `T_(1)` and the outer surface is at a lower temperature of `T_(2)`. Calculate the radial heat current if conductivity of the mate- rial is K.
(ii) A cylindrical pipe of length L has two layers of material of conduc- tivity `K_(1)` and `K_(2)`. (see figure). If the inner wall of the cylinder is maintained at `T_(1)` and outer surface is at `T_(2) (lt T_(1))`, calcu- late the radial rate of heat flow.
 04:07View Solution
04:07View SolutionA 3 mm diameter and 5 m long copper wire is insu- lated using a 2 mm thick plastic cover whose thermal con- ductivity is `K = 0.15 Wm^(-1)K^(-1)`. The wire has a potential difference of 10 V between its ends and the current through it is 8A. The outer surface of the wire is at `30^(@)C`. Neglect convection.
(i) Calculate the temperature at the interface of the wire and the plastic cover.
(ii) Determine whether doubling the thickness of the plastic cover will increase or decrease the interface temperature. [Given `ln(2.33)=0.85`]03:07View SolutionA potato at initial temperature `T_(0)` is placed inside a hot convection oven maintained at a constant temperature `T_(1)(gt T-(0))`. Assume that the potato receives heat only because of convection phenomenon and the rate at which it receives heat is given as hA `(T_(1) – T)` where h is a constant, A is surface area of the potato and T is instantaneous temperature of the potato. Mass and specific heat capacity of the potato are m and s respectively. In how much time the potato will be at a temperature `T_(2)=(T_(0)+T_(1))/(2)` ? Assume no change in volume of the potato.
02:56View SolutionWhat is emissivity of a perfectly reflecting surface?
View SolutionA body is in thermal equilibrium with surrounding. Absorptive power of the surface of the body is a `= 0.5`. E is the radiant energy incident in unit time on the surface of the body. How much energy propagates from its surface in unit time?
01:54View SolutionA copper sphere is maintained at 500 K temperature by connecting it to a battery of emf `V_(1) = 100` V (see figure). The surrounding temperature is 300 K. When half the surface of the copper sphere is completely blackened (so that the surface behaves almost like a black body), a cell of emf `V_(2)` = 141 V is needed to maintain its temperature at 500 K. Calculate the emissivity of the copper surface.
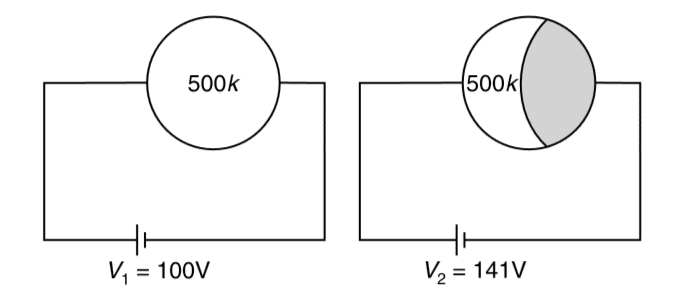 03:04View Solution
03:04View SolutionStefan’s contain (s) derives from other known con- stant of nature, viz. Boltzmann constant, (k) planck’s con- stant (h) and speed of light in vacuum (c). Value of the constant is
`sigma=5.67xx10^(-8)Js^(-1)m^(-2)K^(-4)`
If speed of light were `2%` more than its present value, how much different (in percentage) the value of `sigma` would have been?03:16View SolutionAn iron ball is heated to `727^(@)C` and it appears bright red. The plot of energy density distribution versus wavelength is as shown. The graph encloses an area `A_(0)` under it. Now the ball is heated further and it appears bright yellow. Find the area (A) of the energy density graph now.
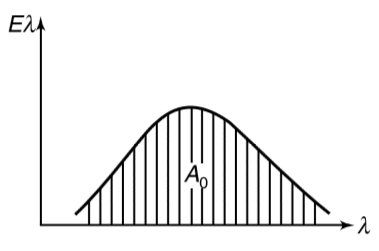
If the given that wavelengths for red and yellow light are 8000 Å and 6000 Å respectively.02:45View SolutionA solid cylinder and a sphere of same material are suspended in a room turn by turn, after heating them to the same temperature. The cylinder and the sphere have same radius and same surface area.
(a) Find the ratio of initial rate of cooling of the sphere to that of the cylinder.
(b) Will the ratio change if both the sphere and the cylinder are painted with a thin layer of lamp black?04:32View SolutionA block body at temperature T radiates same amount of energy in the wavelength range `lambda_(1)` to `lambda_(1)+Deltalambda` and `lambda_(2)` to `lambda_(2)+Deltalambda`. It is given that `Deltaltltlambda_(1)` or `lambda_(2)` and `lambda_(2)gtlambda_(1)`. Prove that `(b)/(lambda_(1))gtTgt(b)/(lambda_(2))` where b is Wien's constant.
03:12View SolutionMajority of radiation from the Sun is in visible and near infra-red `(0.7 t o 4 mum)` region. What can you say about the composition of the radiation from the Earth?
01:48View SolutionA metal ball of mass 1.0 kg is kept in a room at `15^(@)C`. It is heated using a heater. The heater supplies heat to the ball at a constant rate of 24 W. The temperature of the ball rises as shown in the graph. Assume that the rate of heat loss from the surface of the ball to the surrounding is proportional to the temperature difference between the ball and the surrounding. Calculate the rate of heat loss from the ball when it was at temperature of `20^(@)C`.
 03:10View Solution
03:10View SolutionA hot body is suspended inside a room that is maintained at a constant temperature. The temperature difference between the body and the surrounding becomes half in a time interval `t_(0)`. In how much time the temperature difference between the body and the surrounding will becomes `(1)/(4)` the original value?
04:37View SolutionNewton’s law of cooling says that the rate of cooling of a body is proportional to the temperature difference between the body and its surrounding when the difference in temperature is small.
(a) Will it be reasonable to assume that the rate of heating of a body is proportional to temperature difference between the surrounding and the body (for small difference in temperature) when the body is placed in a surrounding having higher temperature than the body?
(b) Assuming that our assumption made in (a) is correct estimate the time required for a cup of cold coffee to gain temperature from `10^(@)C` to `15^(@)C` when it is kept in a room having temperature `25^(@)C`. It was observed that the temperature of the cup increases from `5^(@)C` to `10^(@)C` in 4 min04:12View Solution“Blue hot is hotter than red hot”. Explain.
01:37View SolutionA planet of radius `r_(0)` is at a distance r from the sun `(r gtgt r_(0))`. The sun has radius R. Temperature of the planet is `T_(0)`, and that of the surface of the sun is `T_(s)`. Calculate the temperature of another planet whose radius is `2r_(0)` and which is at a distance 2r from the sun. Assume that the sun and the planets are black bodies.
04:40View SolutionA star having radius R has a small planet revolving around it at a distance d `(gtgt R)`. The star and the planet both behave like black bodies and radiate maximum amount of energy at wavelength `lambda_(s)` and `lambda_(p)` respectively.
(i) Find d in terms of other given parameters.
(ii) Show that `lambda_(p)gtgtlambda_(s) `05:43View SolutionA 20 mm diameter copper pipe is used to carry heated water. The external surface of the pipe is at `T = 80^(@)C` and its surrounding is at `T_(0) = 20^(@)C`. The outer surface of the pipe radiates like a black body and also loses heat due to convection. The convective heat loss per unit area per unit time is given by `h(T – T_(0))` where h = 6 W `(m^(2)K)^(-1)`. Calculate the total heat lost by the pipe in unit time for one meter of its length.
04:24View SolutionSolar constant, `I_(s)` is defined as intensity of solar radiation incident on the Earth. Its value is close to `1.4 kW//m^(2)`. Nearly `68%` of this energy is absorbed by the Earth. The average temperature of Earth is about 290 K. Radius of the Earth is `R_(e) = 6000 km` and that of the Sun is `R_(s) = 700,000 km`. Earth - Sun distance is `r = 1.5 xx 10_(8) km`. Assume Sun to be a black body.
(a) Estimate the effective emissivity of earth.
(b) Find the power of the sun.
(c) Estimate the surface temperature of the Sun.04:45View SolutionA tapering rod of length L has cross sectional radii of a and `b(lt a)` at its two ends. Its thermal conductivity is k. The end with radius a is maintained at a higher temperature `T_(1)` and the other end is maintained at a lower temperature `T_(2)`. The curved surface is insulated.
(i) At which of the two points` – 1` and `2 –` shown in the figure will the temperature gradient be higher?
(ii) Calculate the thermal resistance of the rod.
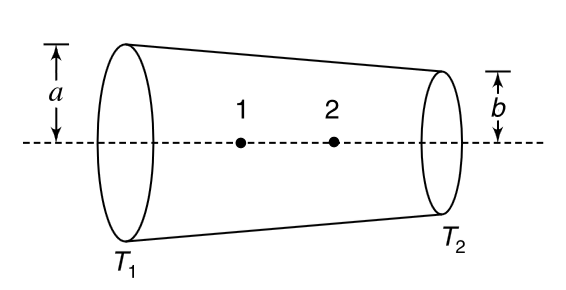 04:23View Solution
04:23View SolutionA thick cylindrical shell made of material of thermal conductivity k has inner and outer radii r and R respectively and its length is L. When the curved surface of the cylinder are lagged (i.e., given insulation cover) and one end is maintained at temperature `T_(1)` and the other end is maintained at `T_(2)(lt T_(1))`, the heat current along the length of the cylinder is H. In another experiment the two ends are lagged and the inner wall and outer wall are maintained at `T_(1)` and `T_(2)` respectively. Find the radial heat flow in this case.
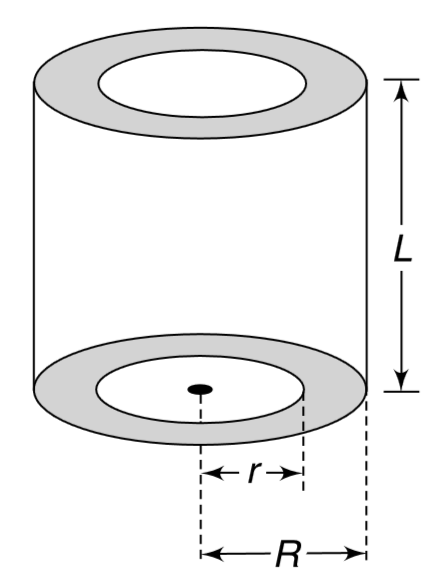 06:53View Solution
06:53View SolutionA double pan window used for insulating a room thermally from outside consists of two glass sheets each of area 1 `m^(2)` and thickness `0.01m` separated by `0.05` m thick stagnant air space. In the steady state, the room-glass interface and the glass-outdoor interface are at constant temperatures of `27^(@)C` and `0^(@)C` respectively. The thermal conductivity of glass is `0.8 Wm^(-1)K^(-1)` and of air `0.08 Wm^(-1)K^(-1)`. Answer the following questions.
(a) Calculate the temperature of the inner glass-air interface.
(b) Calculate the temperature of the outer glass-air interface.
(c) Calculate the rate of flow of heat through the window pane.07:06View SolutionThe container A contains ice at `O^(@)C`. A conducting uniform rod PQ of length 4R is used to transfer heat to the ice in the container. The end P of the rod is maintained at `100^(@)C` and the other end Q is kept inside container A. The complete ice melts in 23 minutes. In another experiment, two conductors in shape of quarter circle of radii 2R and R are welded to the conductor PQ at M and N respectively and their other ends are inserted inside the container A. All conductors are made of same material and have same cross sectional area. Once again the end P is maintained at `100^(@)C` and this time the com- plete ice melts in t min- ute. Find t. Assume no heat loss from the curved surface of the rods. [Take `pi~=3.0`]
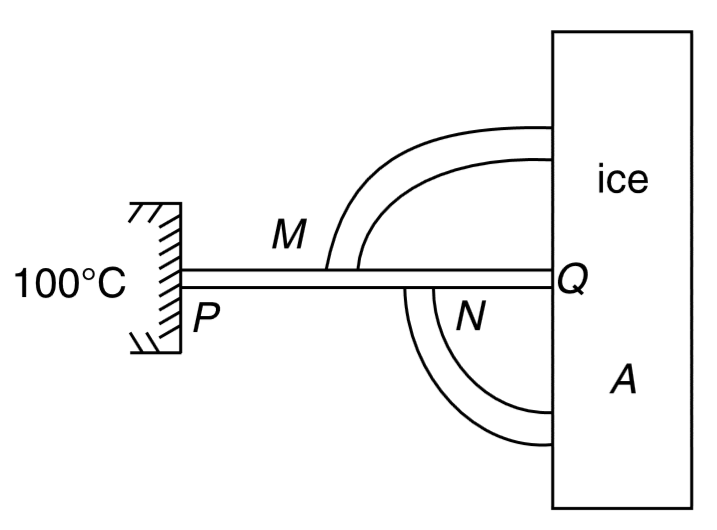 08:55View Solution
08:55View SolutionTwo identical adiabatic containers of negligible heat capacity are connected by conducting rod of length L and cross sectional area A. Thermal conductivity of the rod is k and its curved cylindrical surface is well insulated from the surrounding. Heat capacity of the rod is also negligible. One container is filled with n moles of helium at temperature `T_(1)` and the other one is filled with equal number of moles of hydrogen at temperature `T_(2) (lt T_(1))`. Calculate the time after which the temperature difference between two gases will becomes half the initial difference.
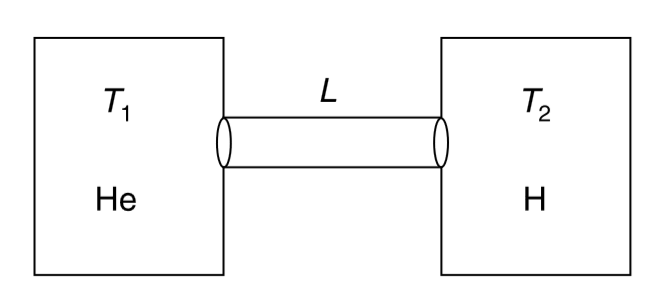 06:34View Solution
06:34View SolutionA copper slab is 2 mm thick. It is protected by a 2 mm layer of stainless steel on both sides. The temperature on one side of this composite slab is `400^(@)C` and `200^(@)C` on the other side. Value of thermal conductivities are-
`k_(cu)=400 Wm^(-1)K^(-1) ` and `k_(s)=16 Wm^(-1)K^(-1)`
(a) Just by knowing that thermal conductivity of steel is much less than copper, find (approximately) the temperature of the copper slab.
(b) Plot the variation of temperature across the thickness of the composite wall.06:50View SolutionA steel plate is `0.3 m` long, `0.1m` wide and `0.012 m` thick. The plate is placed on a heating plate of identical size maintained at `100^(@)C`. The heating plate is receiving energy through a 50 W heater. The heating plate losses heat only to the steel plate which is well insulated from all sides except at the top. The top surface of the steel plate is exposed to an airstream of temperature `20^(@)C`. The top surface of the steel plate radiates like a black body. Calculate the rate at which the top surface looses heat due to convection. The surface of steel plate in contact with heating plate is at `100^(@)C`. Thermal conductivity of steel `k = 16 Wm^(-1)K^(-1)` Stefan’s constant `=5.67xx10^(-8)Wm^(-2)K^(-4)`
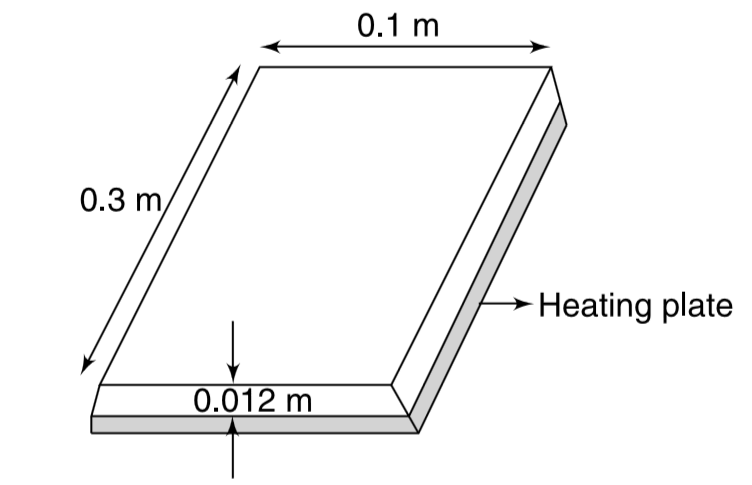 04:30View Solution
04:30View SolutionA straight cylindrical wire is connected to a battery. The wire is maintained at constant temperature of `T_(1)` when the room temperature is `T_(0)(ltT_(1))`. The wire is disconnected from the battery and half of it is cut-off. The remaining half of the wire is connected to the same battery in the same room. Find the constant temperature `(T_(2))` attained by the wire. Assume that wire loses heat to the atmosphere through radiation from curved surface only.
02:39View SolutionA spherical shell is kept in an atmosphere at temperature `T_(0)`. The wavelength corresponding to maximum intensity of radiation for the shell is `lambda_(0)`. A point source of constant power is switched on inside the shell. The power radiated by the source is `P = 04sigmaSeT_(0)^(4)` where S, e and `sigma` are outer surface area of the shell, emissivity of the outer surface of the shell and Stefan’s constant respectively. Calculate the new wavelength `(lambda)` corresponding to the maximum intensity of radiation from the shell. Assume that change in temperature `(DeltaT)` of the shell is small compared to the ambient temperature `T_(0)`.
03:57View SolutionA body at a temperature of `50^(@)C `cools to `49^(@)C` in time `Deltat` when it is placed in a room maintained at `- 3^(@)C`. The same body cools from `50^(@)C` to `49^(@)C` in time `Deltat'` when placed in a room that is maintained at `24^(@)C`. Find `Deltat'` in terms of `Deltat`. Assume heat loss through radiation only and the specific heat capacity of the body remains constant with change in temperature.
04:35View SolutionA plane surface A is at a constant temperature `T_(1)`` = 1000 K`. Another surface B parallel to A, is at a constant lower temperature `T_(2) = 300 K`. There is no medium in the space between two surfaces. The rate of energy transfer from A to B is equal to `r_(1)(J/s)`. In order to reduce rate of heat flow due to radiation, a heat shield consisting of two thin plates C and D, thermally insulated from each other, is placed between A and B in parallel. Now the rate of heat transfer (in steady state) reduces to `r_(2)`. Neglect any effect due to finite size of the surfaces, assume all surfaces to be black bodies and take Stefan’s constant `sigma = 6 xx 10^(- )8 Wm^(- 2)K^(-4)`. Area of all surfaces `A = 1m^(2)`.
(i) Find `r^(1)`
(ii) Find the ratio `(r^(2))/(r^(1))`
(iii)Find the ratio `(r^E(2))/(r_(1))` if temperature of A and B were 2000 K 600 K respectively.
 06:43View Solution
06:43View SolutionA block is kept in a room which is at `20^(@)C`. To raise the temperature of the block, heat is given to it at a constant rate of 600 watt (using an electric heater). The temperature of the block rises with time as shown in the graph. The slope of the graph at time `t = 0` is `3^(@)C s^(-1)`. Once the temperature rises to `60^(@)C`, the heater is switched off and another heater is switched on to maintain the temperature of the block at `60^(@)C`. This new heater supplies heat at a constant rate of 100 watt. Assume that heat capacity of the block remains constant for the range of temperature involved.
(a) Explain why the slope of the given graph is decreasing with time.
(b) Calculate the heat capacity of the block.
(c) If the 100 W heater is also switched off, what will be initial rate of cooling of the block?
(d) Assuming that rate of heat loss by the block to the surrounding is proportional to difference in its temperature with surrounding, calculate the heat radiated per second by the block when it was at `30^(@)C`.
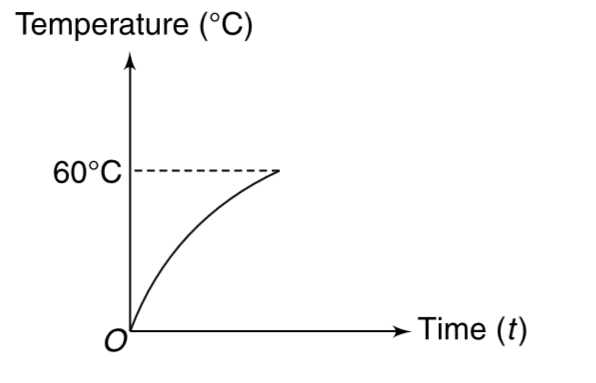 04:35View Solution
04:35View SolutionMass m of a liquid A is kept in a cup and it is at a temperature of `90^(@)C`. When placed in a room having temperature of `20^(@)C`, it takes 5 min for the temperature of the liquid to drop to `30^(@)C`. Another liquid B has nearly same density as that of A and its sample of mass m kept in another identical cup at `50^(@)C` takes 5 min for its temperature to fall to `30^(@)C` when placed in room having temperature `20^(@)C`. If the two liquids at `90^(@)C` and `50^(@)C` are mixed in a calorimeter where no heat is allowed to leak, find the final temperature of the mixture. Assume that Newton’s law of cooling is applicable for given temperature ranges.
04:52View SolutionConsider the Sun to be a black body at temperature `T_(S) = 5780 K`. Radius of the Sun is `r_(S) = 6.96 xx 108 m`. The Earth - Sun distance is `R = 1.49 xx 1011m`. Assume that `30%` of the solar radiation that hits the earth is scattered back into space without absorption.
(a) Calculate the steady state average temperature of the earth assuming it to be a black body. Take `(0.7 )^((1)/(4))= 0.91`
(b) We know that average temperature of earth is `~=288K`. How does this value compare with that obtained in (a)? The difference is due to greenhouse effect. Comment on the following statement - “Emissivity of earth is reduced more than absorptivity due to green house effect.”05:37View SolutionA and B are two sphere made of same material. Radius of A is double that of B and initially they are at same temperature (T). Both of them are kept far apart in a room at temperature `T_(0)(lt T)`. Calculate the ratio of initial rate of cooling (i.e. rate of fall of temperature) of sphere A and B if
(a) the spheres are solid,
(b) the spheres are hollow made of thin sheets of same thickness04:28View SolutionHeat received by the Earth due to solar radiations is `1.35 KWm^(-2)`. It is also known that the temperature of the Earth’s crust increases `1^(@)C` for every 30 m of depth. The average thermal conductivity of the Earth’s crust is `K = 0.75 J (msK)^(-1)` and radius of the Earth is `R = 6400 km`.
(i) Calculate rate of heat loss by the Earth’s core due to conduction.
(ii) Assuming that the Earth is a perfect block body estimate the temperature of its surface.03:59View SolutionA truck of mass M has 4 wheels. The surface area of the metal disc in each wheel is A. When brakes are applied the brake shoe in each wheel rubs against the metal disc. This produces heat. We will assume that this heat is used to heat the disc in the wheel only. Each disc has mass m and is made of material of specific heat capacity s. One day the truck was going downhill on a road inclined at angle `theta` to the horizontal. To maintain a constant speed v the driver had to apply brakes. The only other dissipative force, apart from the brake force, on the truck is the air resistance force that is equal to F. Assume no heating of discs due to air friction.
(a) Find the initial rate of rise of temperature of each metal disc after the brakes are applied.
(b) Find the final temperature (T) of the disc assuming that it is a black body and it loses heat only through radia- tion. Take the atmospheric temperature to be `T_(0)`05:03View SolutionA solid body A of mass m and specific heat capacity ‘s’ has temperature `T_(1) = 400 K`. It is placed, at time `t = 0`, in atmosphere having temperature `T_(0) = 300 K`. It cools, following Newton’s law of cooling and its temperature was found to be `T_(2) = 350 K `at time `t_(0)`. At time `t_(0)`, the body A is connected to a large water bath maintained at atmospheric temperature `T_(0)`, using a conducting rod of length L, cross section A and thermal conductivity k. The cross sectional area A of the connecting rod is small compared to the overall surface area of body A. Find the temperature of A at time `t = 2t_(0)`.
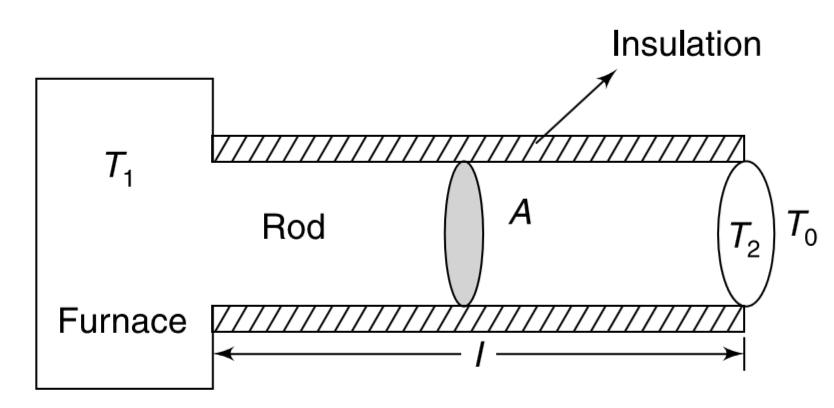
07:49View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is `T_(0)` and the furnace is maintained at `T_(1) = T_(0) + DeltaT_(1)`. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained `T_(2) = T_(0) + DeltaT_(2) [DeltaT_(2) ltlt T_(0)]`. The exposed surface of the rod has emissivity e. Prove that `DeltaT_(1)` is proportional to `DeltaT_(2)` and find the proportionality constant.
 04:05View Solution
04:05View Solution
Heat Transfer questions and complete solutions for chapter HEAT TRANSFER of ARIHANT PHYSICS (HINGLISH) of Class 11
