Complete Solutions to Solved Examples of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| CENGAGE CHEMISTRY | Solved Examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A process in which pressure remians constant is called
02:00View SolutionWhich one of the following is a state property/function?
01:23View SolutionWhich of the following is an extensive property?
07:18View SolutionIf temperature of the system remains constant during the course of change, the change is
02:53View SolutionA process in which volume remians constant is called
01:26View SolutionIdentify intensive property from the following
03:23View SolutionWhich of the following is an extensive property of the system?
02:10View SolutionAn isolated system is that system in which
02:05View SolutionThermodynamic is concerned with
01:08View SolutionInternal enegry of a system of molecules is determined by taking into consideration its
02:30View SolutionA thermodynamic quantity is that
01:30View SolutionThermodynamic equilibrium involves
01:22View SolutionFor an adiabatic process, which of the following relations is correct?
02:12View SolutionTwo liters of `N_(2)` at `0^(@)C` and `5` atm pressure is expanded isothermally against a constant external pressure of `1` atm untill the pressure of gas reaches `1` atm. Assuming gas to be ideal, claculate the work of expansion.
04:09View SolutionCalculate the work done when done when `1.0` mol of water at `373K` vaporises against an atmosheric pressure of `1.0atm`. Assume ideal gas behaviour.
03:11View SolutionIdentify different steps in the following cyclic process:
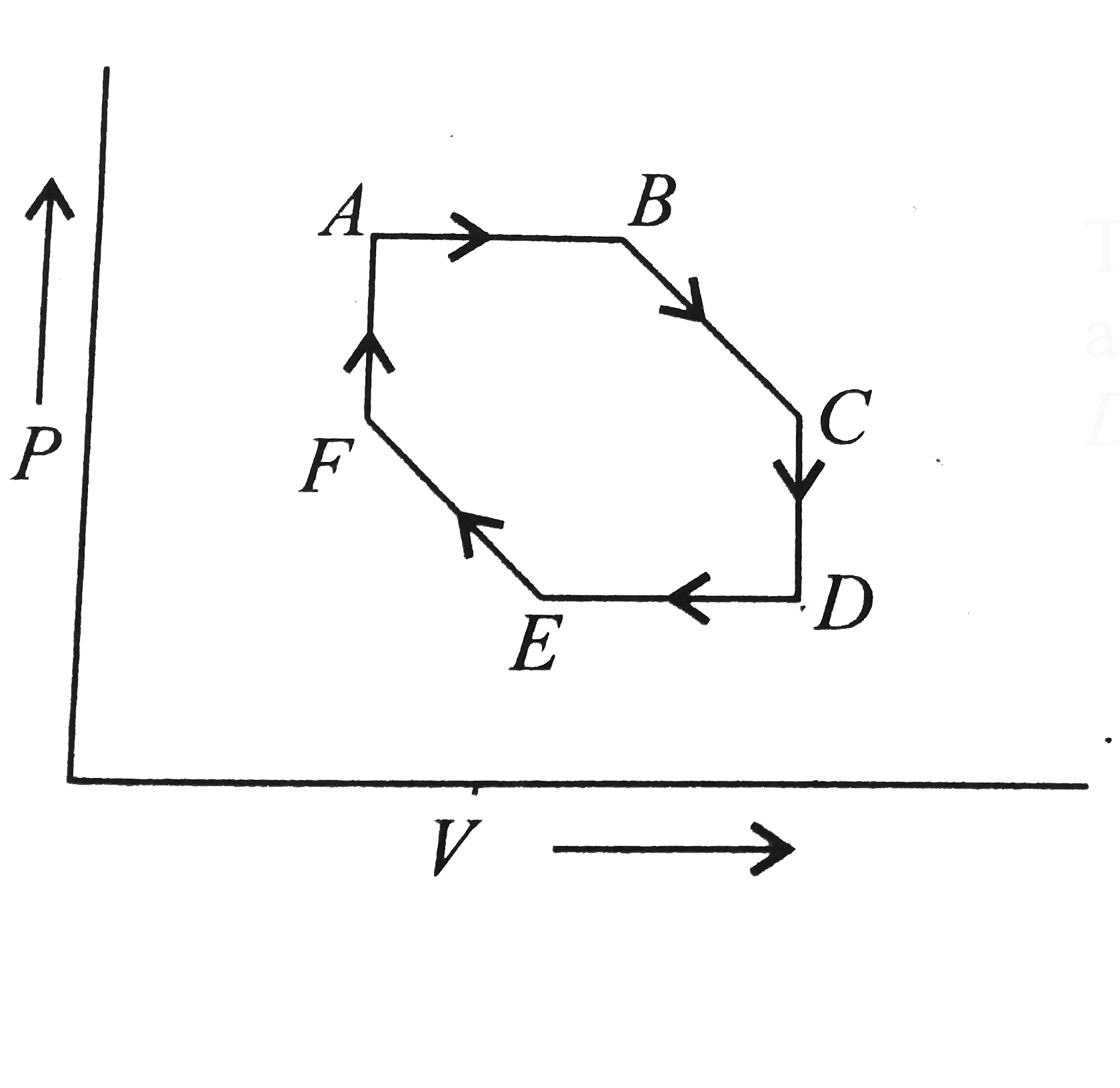 02:31View Solution
02:31View SolutionA gas expands by `0.5L` against a constant pressure of `1 atm`. Calculate the work done in joule and calorie.
03:10View SolutionOne made of an ideal gas is put through a series of changes as shown in the graph in which `A,B,` and `C`, mark the three stages of the system. At each stage the variables are shown in the graph.
a. Calculate the pressure at three stages of system.
b. Name the process during the following chnages:
i. `A` to `B` ii. `B` to `C`
iii. `C`to`A` iv. Overall change
 04:16View Solution
04:16View SolutionA thermodynamic system consists of a cylinder-piston attangement with ideal gas in it. It goes from the state `i` to the state `f` as shwon in the figure. The work done by gas during the process is
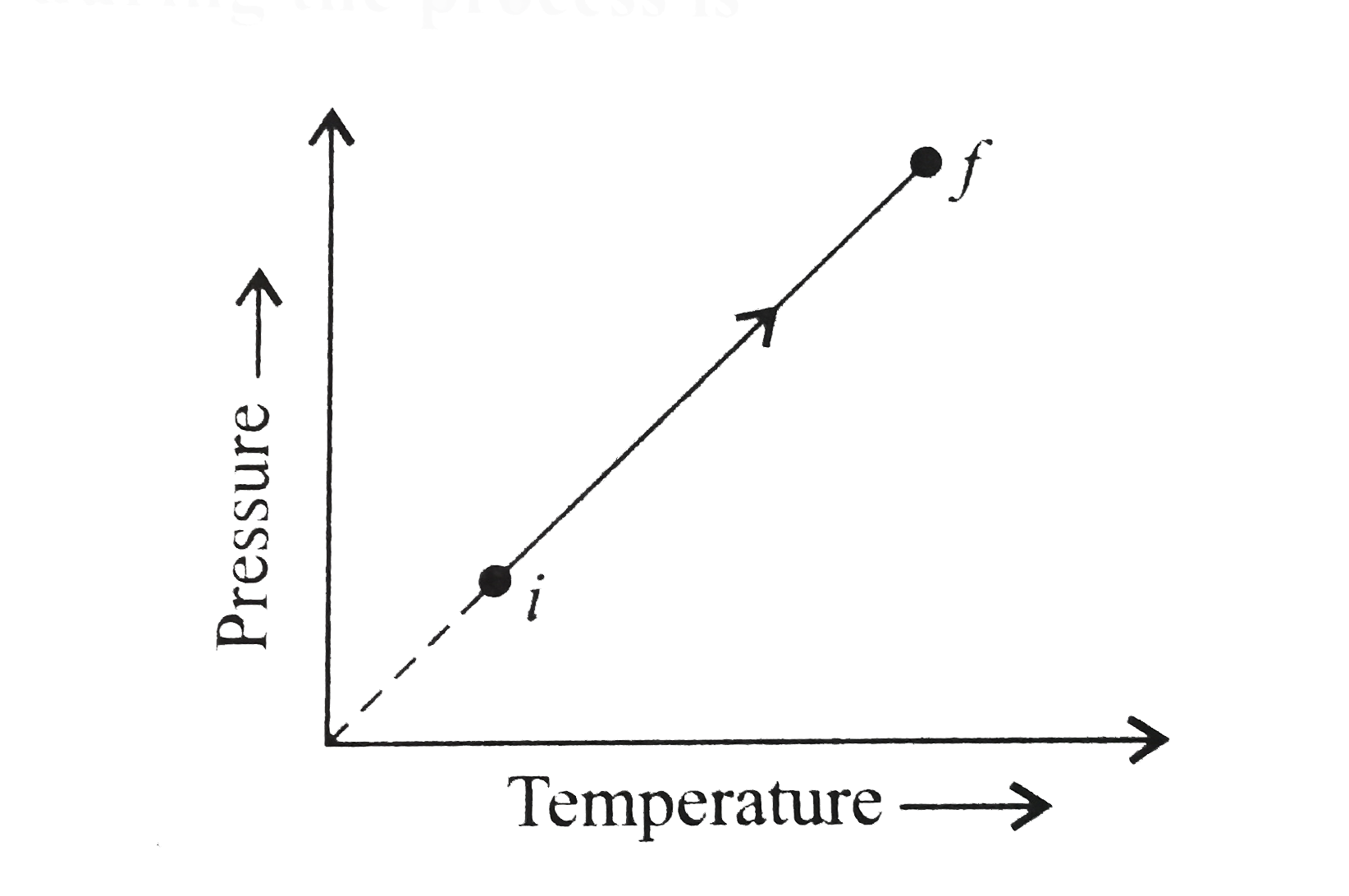 01:14View Solution
01:14View SolutionA cyclie process `ABCA` is shwon in a `V-T` diagram. The corresponding `P-V` diagram is
 03:37View Solution
03:37View SolutionWhich one of the following statements about state function is correct?
06:51View SolutionConsider the modes of transformations of a gas form state `A` to state `B` as shown in the given `P-V` diagram. Which one of the following is true?
 05:18View Solution
05:18View SolutionWhich of the following statements is/are correct?
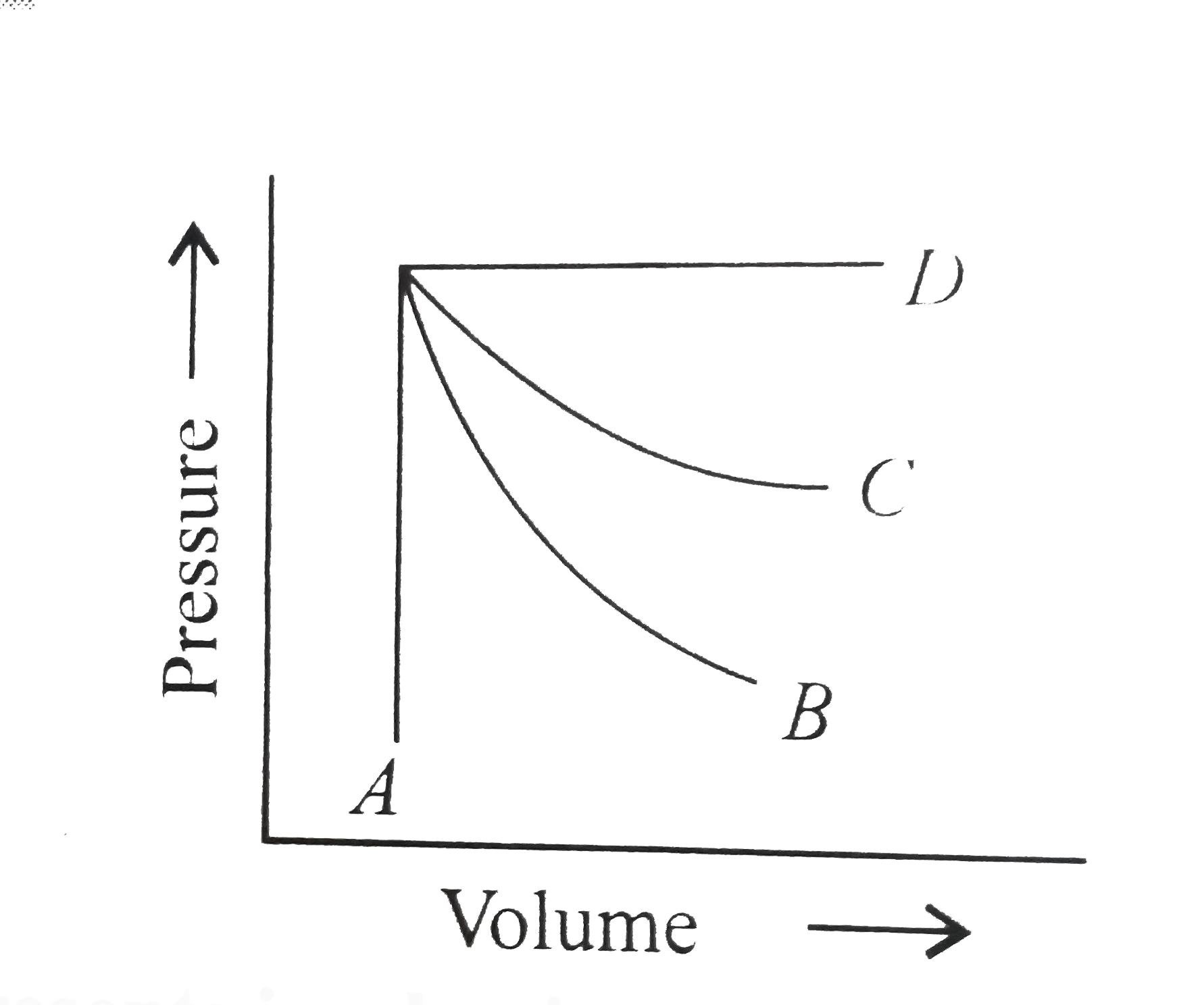 01:07View Solution
01:07View SolutionIn `P-V` diagram shown below,
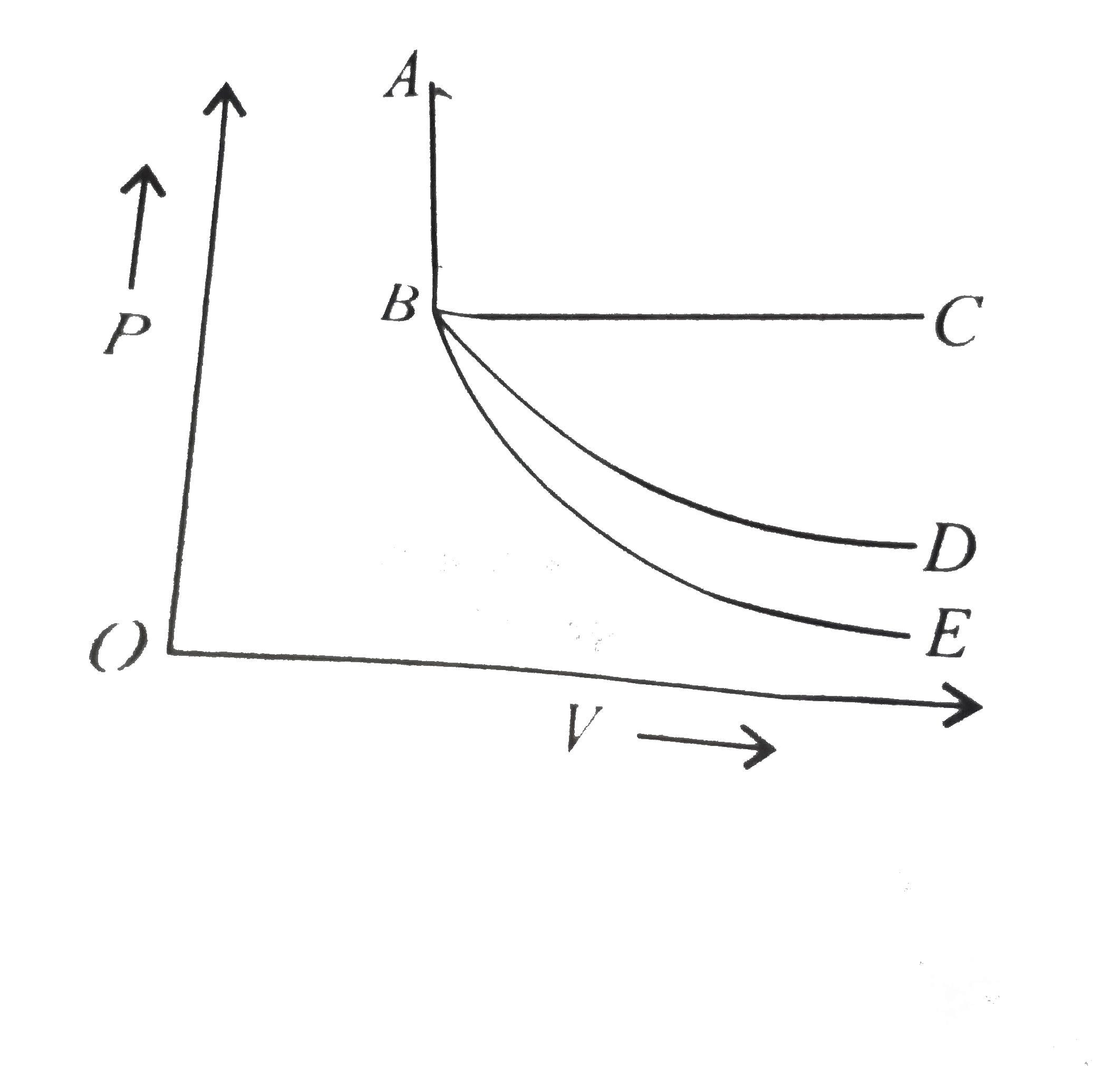 00:58View Solution
00:58View SolutionThe following are the `P-V` diagram for cyclic process for a gas. In which of these processes, heat is not obsorbed by the gas?
01:14View SolutionThe graph betwene `P` and `V` at constant temperature should look like
03:58View SolutionIn the cyclic process shown on `V-P` diagram, the magnitude of the work done is
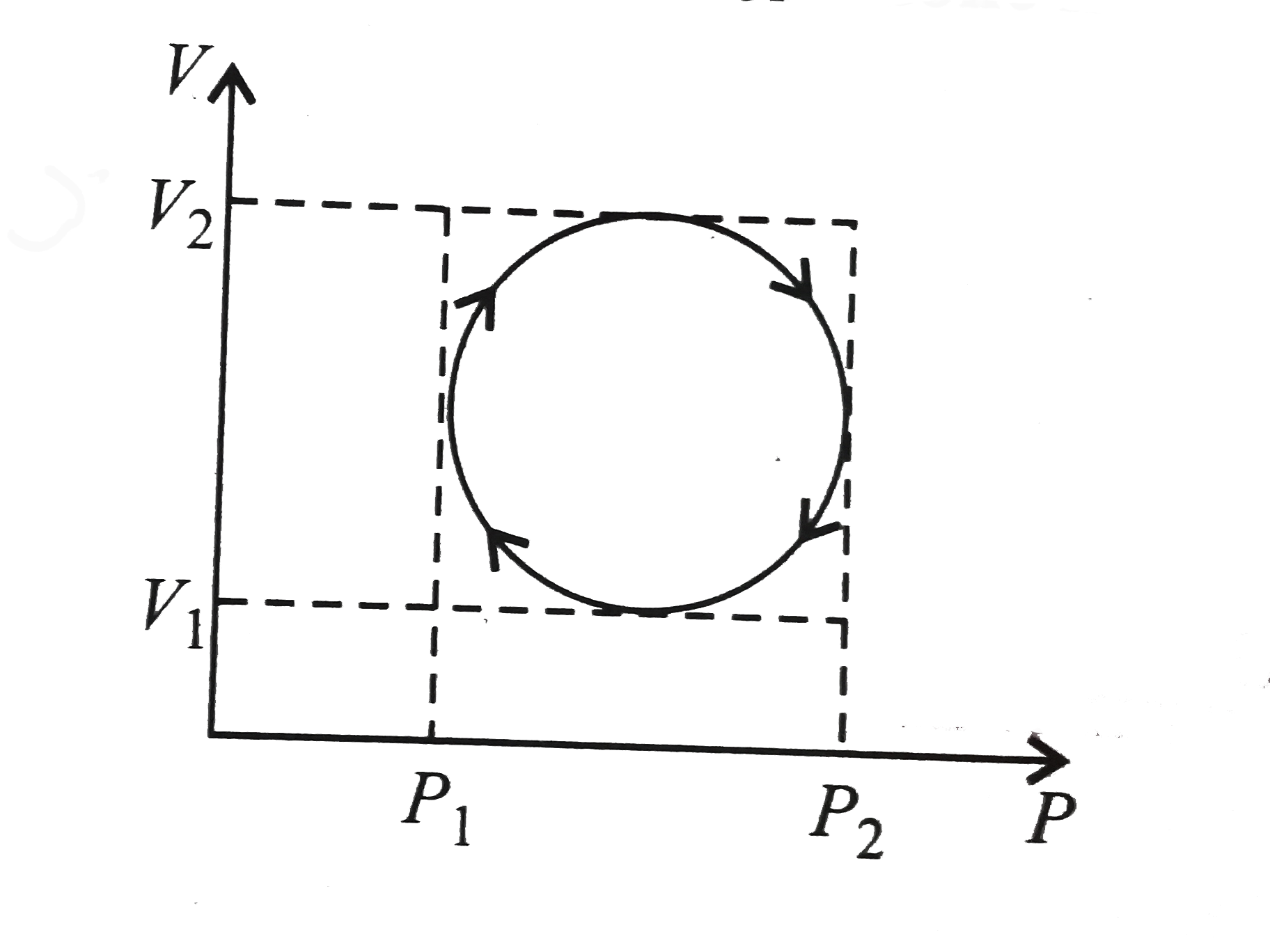 04:14View Solution
04:14View SolutionA cyclic process is shown in the `P-T` diagram.
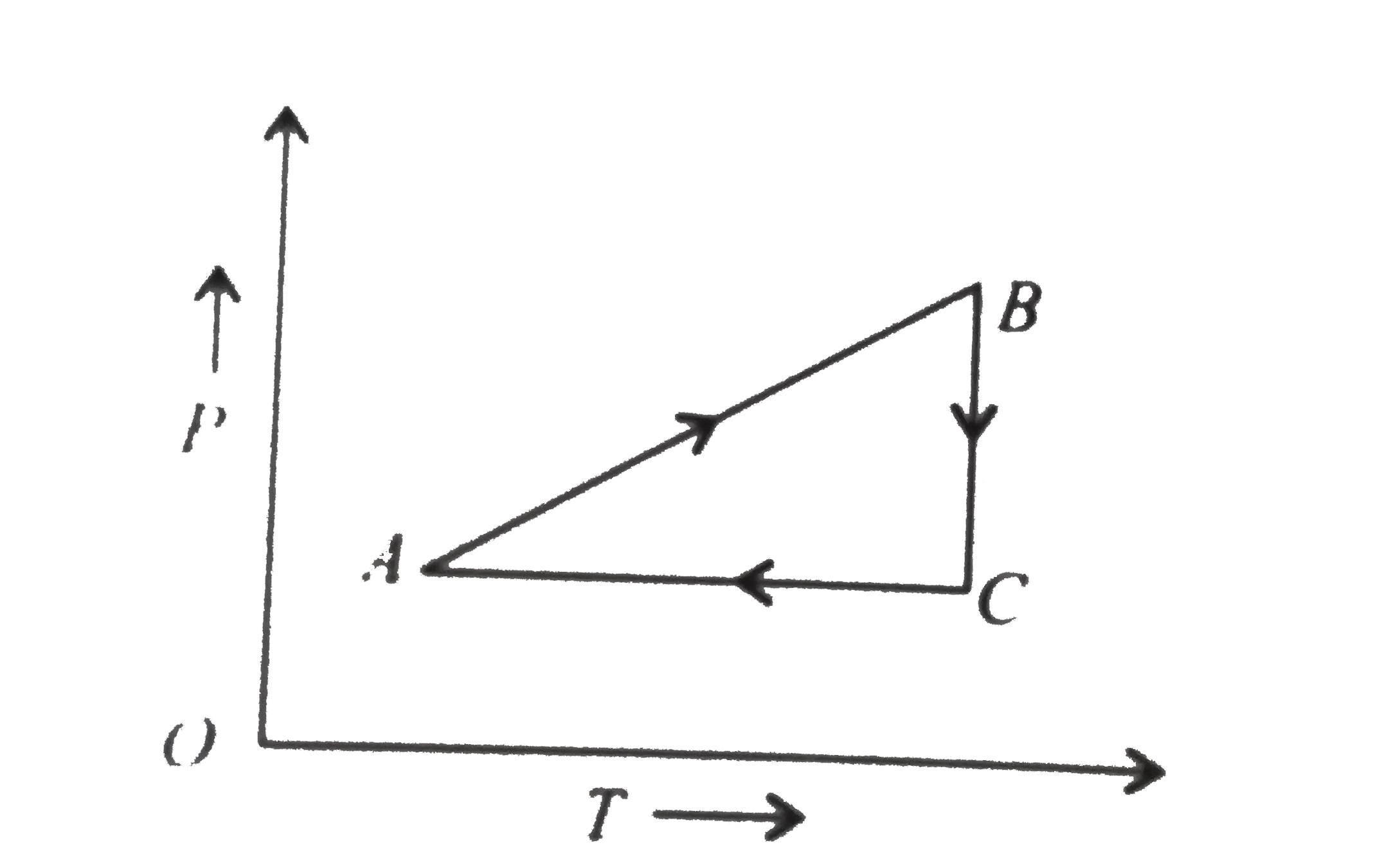
Which of the curve shows the same process on a `V-T` diagram?02:31View SolutionCalculate the work done in open vessel at `300K`, when `92g Na` reacts with water. Assume ideal gas neture.
03:54View SolutionCalculate the work done when a system raises a colume of water of radius `5.0mm` through `10cm`.
02:58View SolutionCalculate the work done when `56g` of iron reacts with hydrochloric acid in `(a)` a closed vessel of fixed volume and `(b)`an open beaker at `25^(@)C`.
05:29View SolutionA system is provided `50J` of heat and work done on the system is `20J`. What is the change in the internal enegry?
02:20View SolutionThe work done by a system is `10J`, when `40J` heat is supplied to it. Calculate the increase in the internal enegry of system.
02:09View SolutionA gas occupies `2L` at `STP`. It is provided `300J` heat so that it volume becomes `2.5L` at `1atm`. Caluclate the change in its internal enegry.
02:15View SolutionA certain electric motor produced `16kJ` of energy each second as mechanical work and lost `3kJ` as heat to the surroundings. What is the change in the internal energy of the motor and its power supply each second?
03:13View SolutionAn insulated container is divided into two equal portions. One portion contains as ideal gas at pressure `P` and tenperature `T`. The othe portion is a perfect vaccume. If a hole is opened between the two portions, claculate
a. the change in internal energy.
b. the change in temperature.03:33View Solution`2.8g` of `N_(2)` gas at `300K` and `20atm` was allowed to expand isothermally against a constant external pressure of `1atm`. Calculate `DeltaU, q,` and `W` for the gas.
04:50View SolutionAt `27^(@)C`, one mole of an ideal gas is compressed isothermally and reversibly from a pressure of `20atm` to `100 atm`. Calculate `DeltaE` and `q.(R = 2 calK^(-1)mol^(-1))`
02:12View SolutionOne mole of an ideal gas is heated at constant pressure from `0^(@)C` to `100^(@)C`.
a. Calculate the work done.
b. If the gas were expanded isothermally and reversibly at `0^(@)C` from `1 atm` to some othe pressure `P`, what must be the final pressure if the maixmum work is equal to the work in `(a)`?03:01View SolutionCalculate the maximum work done in expanding `16g` of oxygen at `300K` occupying volume of `5dm^(3)` and isothermally untill the volume become `25dm^(3)`?
04:19View SolutionCalculate `q,w`, and `DeltaU` for the isothermal reversible expansion of one mole of an ideal gas from an initial pressure of `2.0` bar to a final pressure of `0.2` bar at a constant temperature of `273K`.
05:15View SolutionCalculate the maximum work down when pressure on `10g` of hydrogen is reduced from `20` to `1atm` at a constant temperature of `273K`. The gas behaves ideally. Will there be any change in internal energy. Also calculate `q. (R = 2 cal K^(-1) mol^(-1))`
04:25View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process `ABC` as shown in figure below. Calculate work done
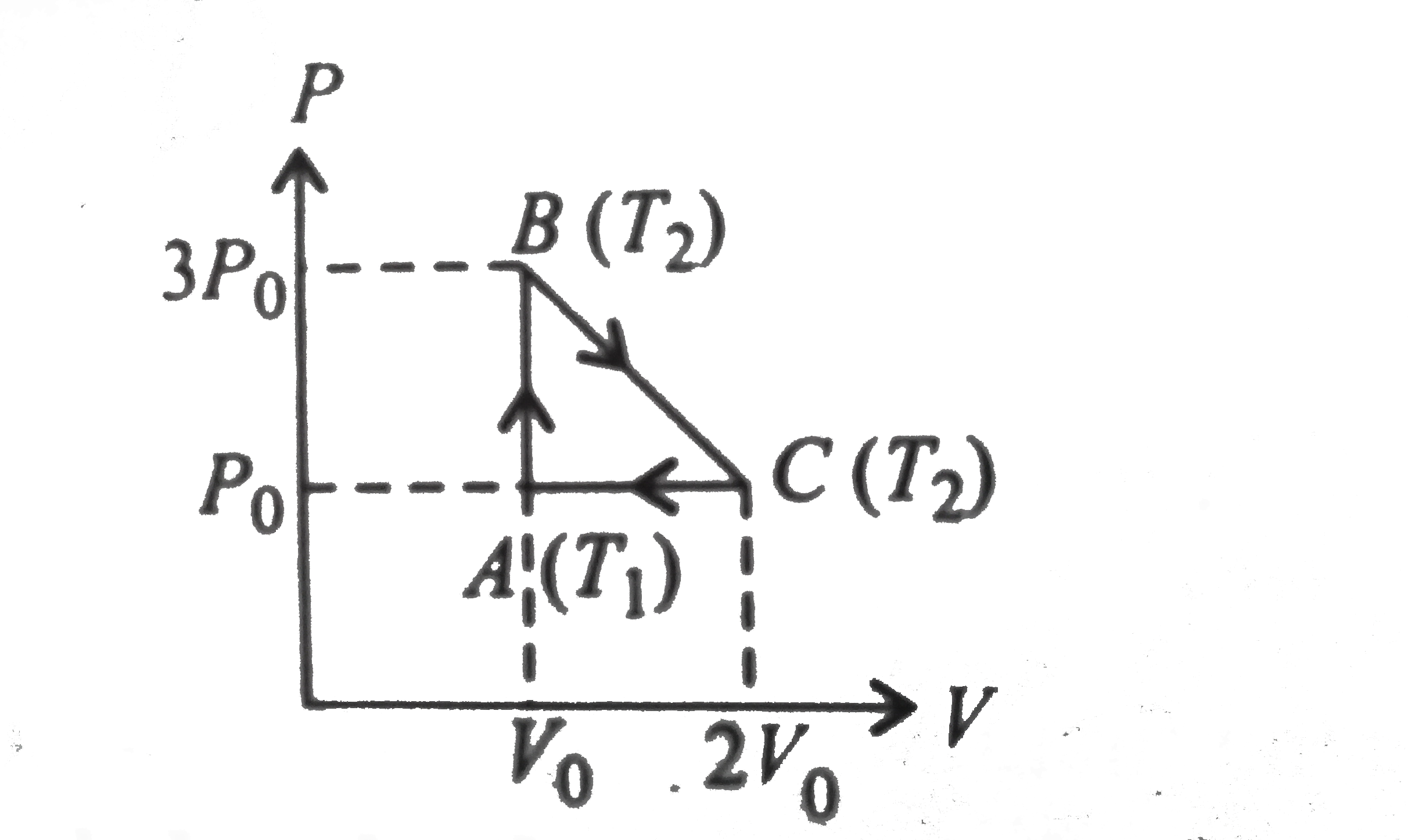 01:35View Solution
01:35View SolutionAn ideal gas absorbs `600cal` of heat during expansion from `10L` to `20L` against the constant pressure of `2atm`. Calculate the change in internal enegry.
03:19View SolutionCalculate the workdone taking place when an ideal gas undergoes isothermal expansion.
06:06View SolutionAn ideal mono-atomic gas follows the path `ABCD`. The work donw during the complete cycle is
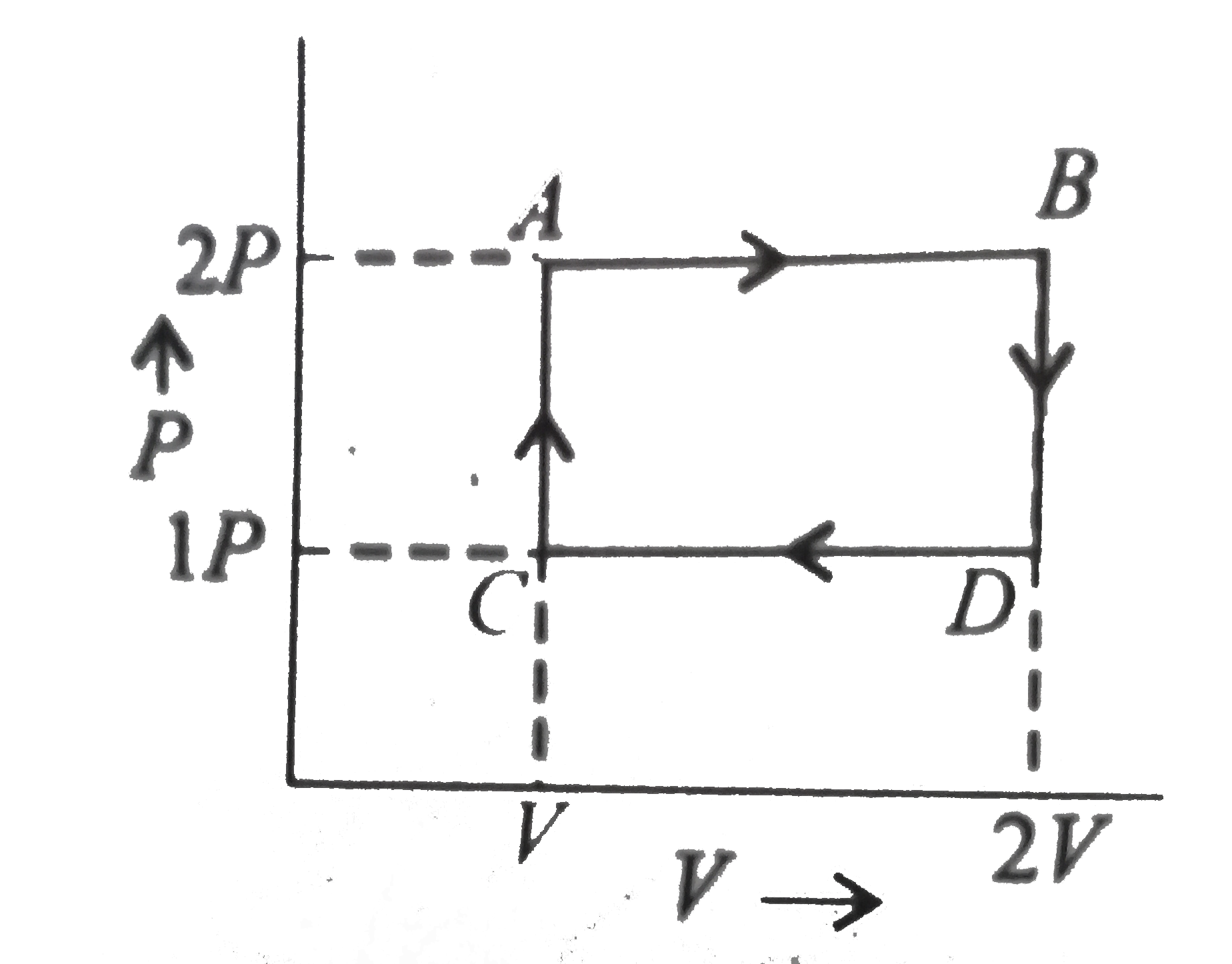 01:12View Solution
01:12View SolutionThe net work done through a series of changes reported in figure for an ideal gas is
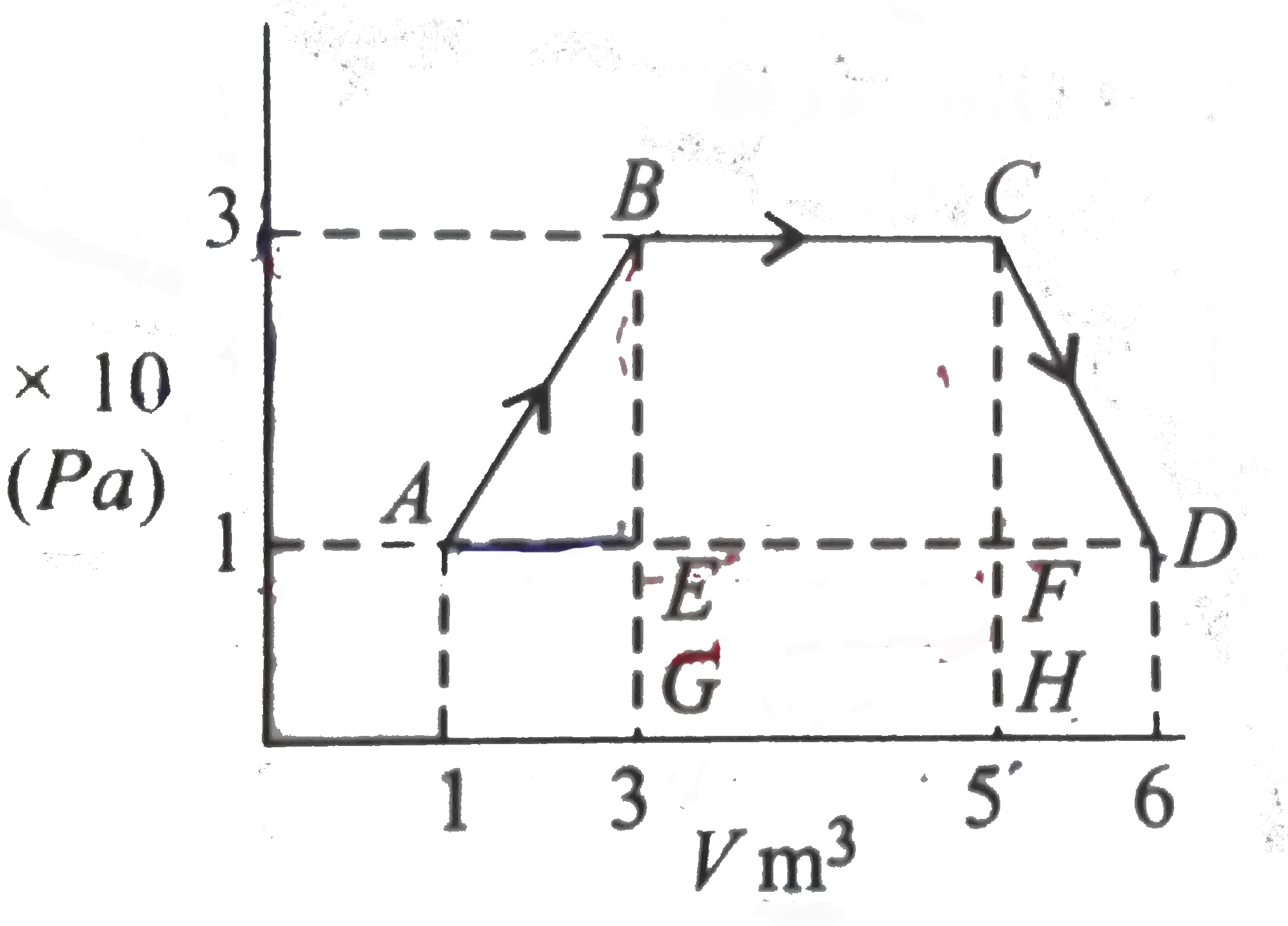 02:04View Solution
02:04View SolutionHeat energy absorbed by a system in going through a cyclic process shown in figure is
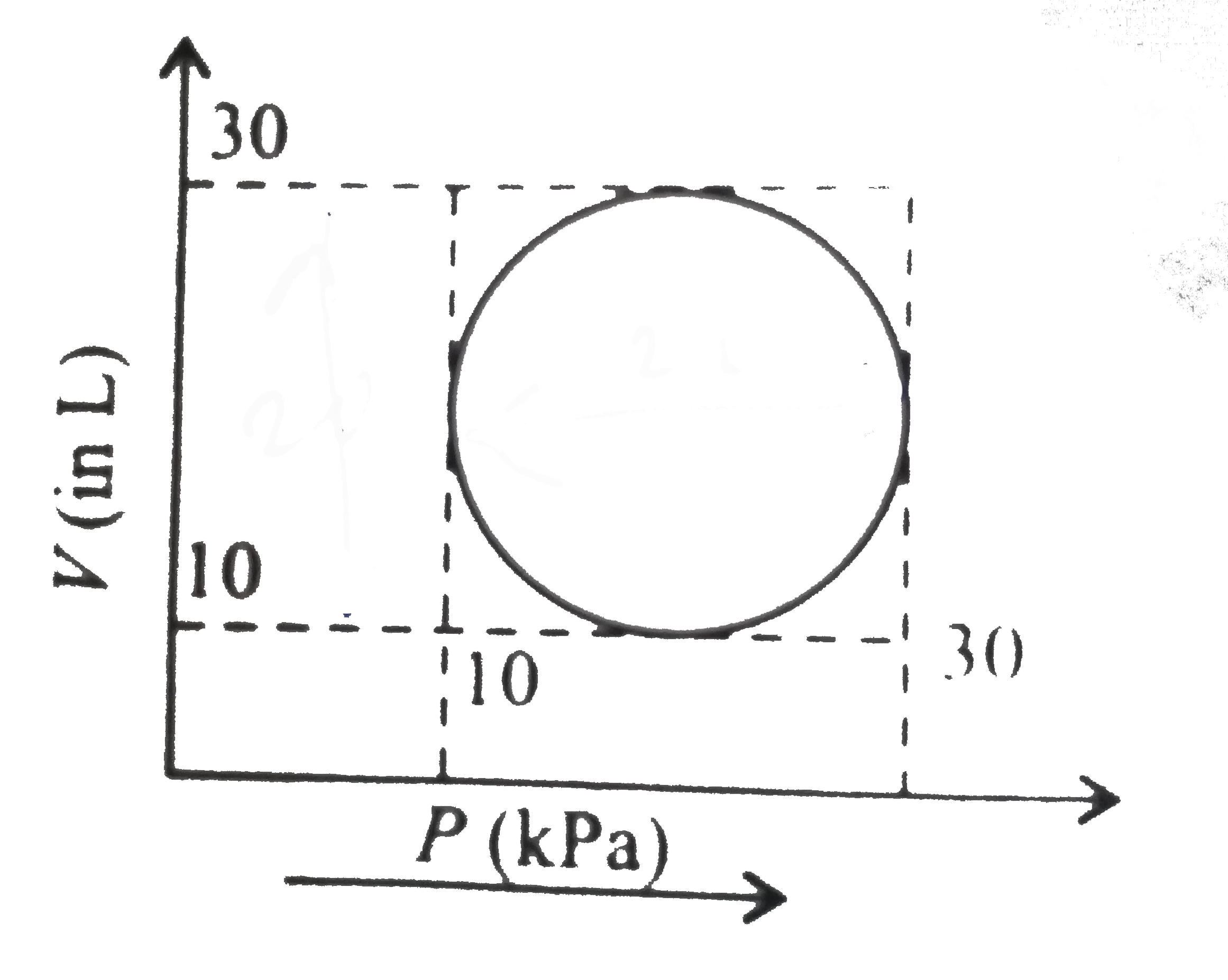 03:11View Solution
03:11View SolutionA given mass of gas expands from state `A` to state `b` by three paths `1,2`, and `3` as shown in the figure below. If `w_(1),w_(2)` and `w_(3)`, respectively, be the work done by the gas along three paths, then
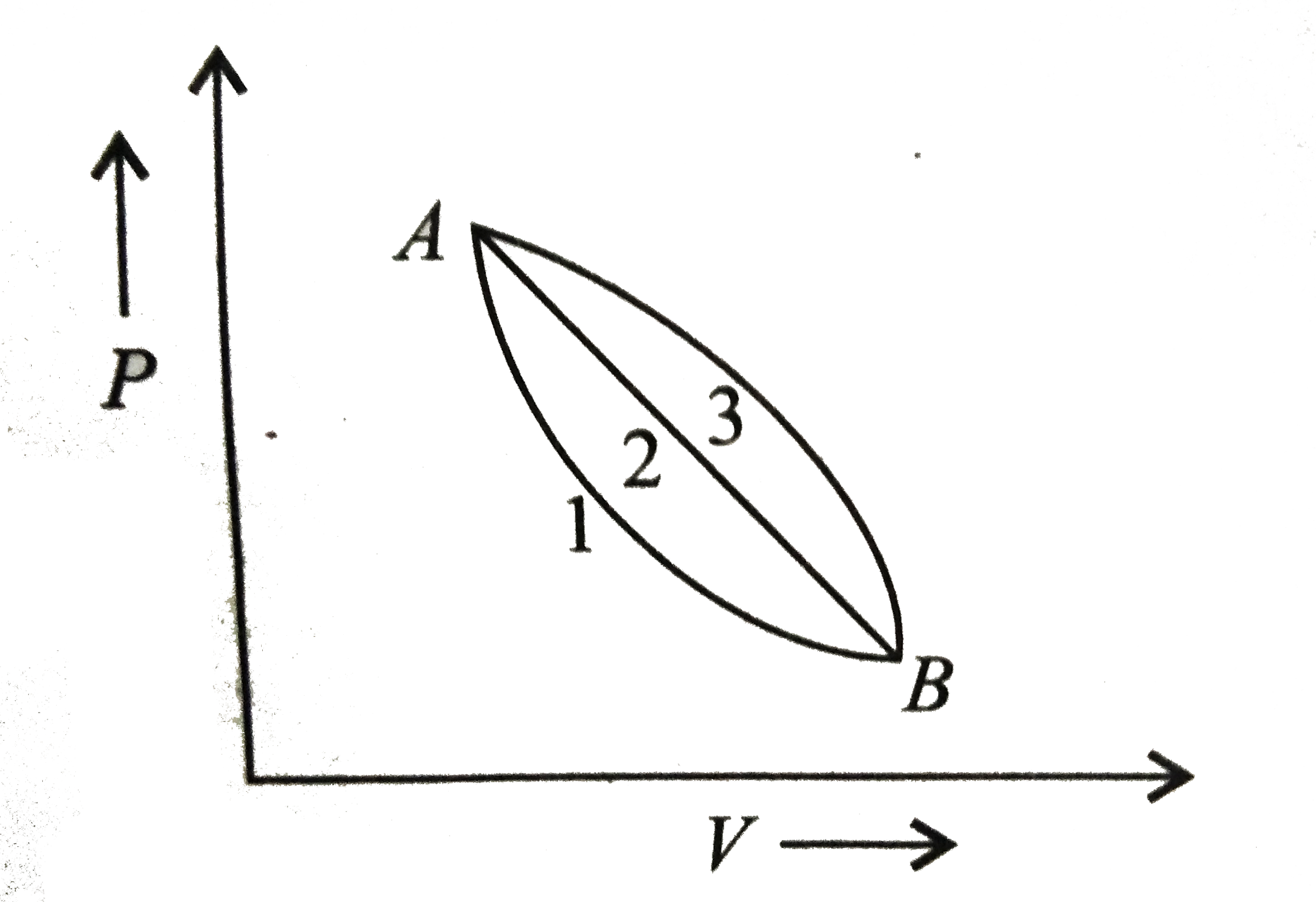 04:56View Solution
04:56View SolutionAn ideal gas is taken around the cycle `ABCD` shown in the `P_V` diagram below. The net work done by the gas during the cycle is equal to
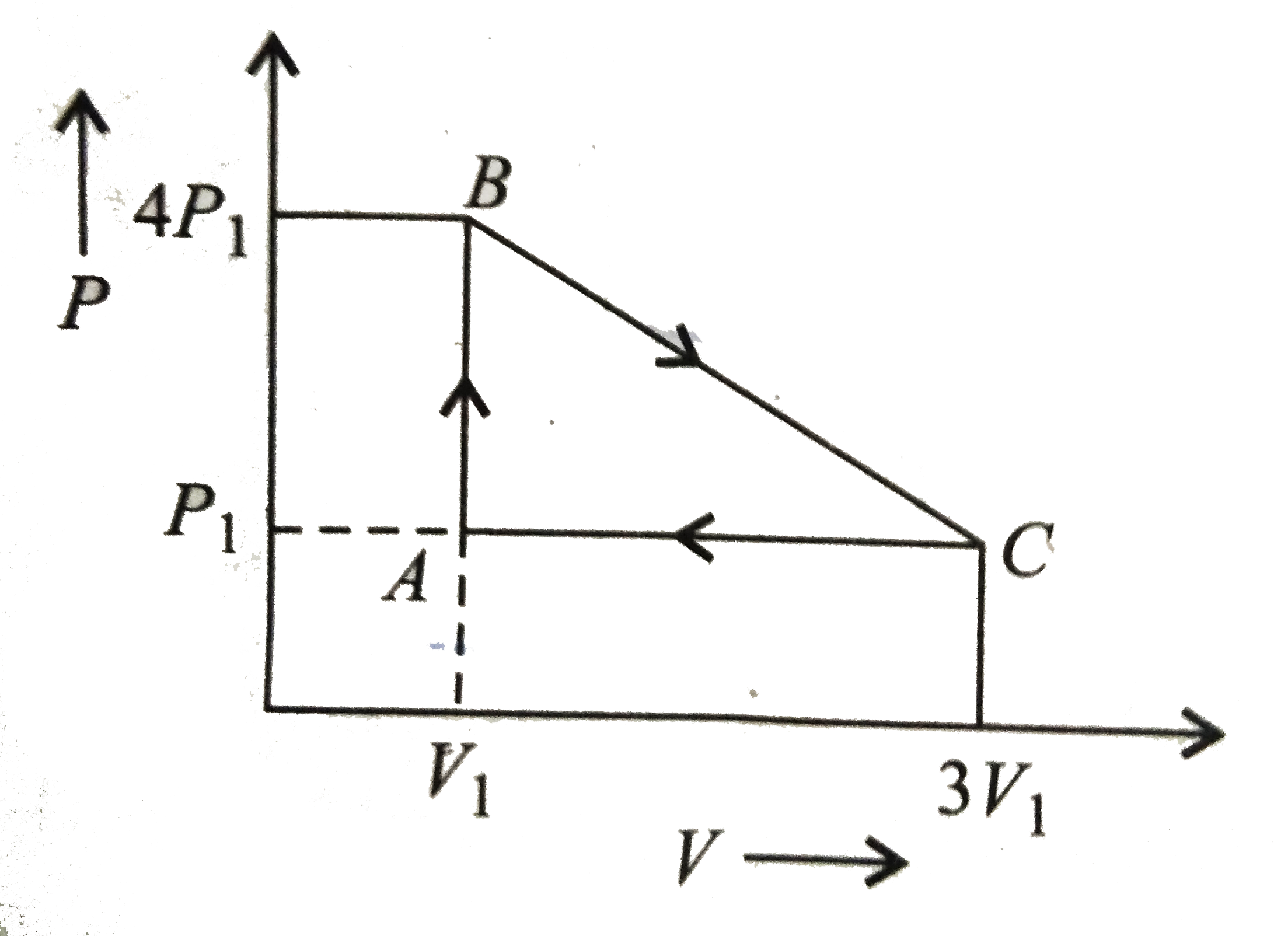 03:41View Solution
03:41View SolutionAn ideal mono-atomic gas follows the path `ABDC`. The work done during the complete cycle is
 01:12View Solution
01:12View SolutionCan we measure the absolute value of internal enegry?
02:02View SolutionOne mole of `SO_(2)` at `298K` and `1atm` pressure is heated in a closed vessel so that its temperature is `475K` and pressure is `4atm`. It is then cooled so that temperature becomes `298K` and pressure is `1atm`. What is that change in the internal energy of the gas?
02:09View SolutionNeither `q` nor `w` is a state function but `q +w` is a state function. Explain why?
00:53View SolutionWhich one of the following is a state property/function?
01:23View SolutionUnder what conditions is the heat of reaction equal to enthalpy change?
02:54View SolutionA gas expands from `3 dm^(3)` to `5dm^(3)` against a constant pressure of `3atm`. The work done during the expansion if used to heat `10mol` of water at temperature `290K`. Find the final temperature of water, if the specific heat of water `= 4.18g^(-1)K^(-1)`.
03:12View SolutionClassify the following as open, closed, or isolated system.
a. A beaker containing as open, boiling water.
b. A chemical reaction taking place in an enclosed flask.
c. A cup of tea placed on a table.
d. Hot water placed in perfectly insulated closed container.
e. A thermos flask containing hot coffee.07:54View SolutionIf `DeltaH` is the enthalpy change and `DeltaU` the change in internal energy accompanying a gaseous reaction, then
03:21View SolutionWater is boiled under a pressure of `1.0 atm`. When an electric current of `0.50A` from a `12V` supply is passed for `300`s through a resistance in thermal contact with it, it is found that `0.789 g` of water is vaporied. Calculate the molar internal enegry and enthalpy chnages at boiling point `(373.15K)`.
03:21View Solution`10g` of argon gas is compressed isothermally and reversibly at a temperature of `27^(@)C` from `10L` to `5L`. Calculate `q, w, DletaU`, and `DeltaH` for this process. `R = 2.0 cal K^(-1) "mol"^(-1), log_(10)2 = 0.30`. Atomic weight of `Ar = 40`.
05:03View SolutionThe internal enegry change in the conversion of `1.0 mol` of the calcite form of `CaCO_(3)` to the aragonite from is `+0.2kJ`. Calculate the enthalpy change when the pressure is 1 bar, given that the densities of the solids are `2.71` and `2.93 gcm^(-3)`, respectively.
03:34View SolutionOne mole of a liquid (`1` bar, `100 mL)` is taken in an adiabatic container and the pressure increase steeply to `100bar`. Then at a constant pressure of `100` bar, volume decreases by `1mL` . Find `DeltaU` and `DeltaH`.
02:46View Solution`(Delta H - Delta U)` for the formation of carbon monoxide `(CO)` from its elements at `298K` is
`(R = 8.314 K^(-1)mol^(-1))`02:07View SolutionThe difference between the heats of reaction at constant pressure and a constant volume for the reaction `2C_(6)H_(6)(l) + 15O_(2)(g) rarr 12CO_(2)(g) + 6H_(2)O(l)` at `25^(@)C` in `kJ` is
02:55View SolutionThe latent heat of vapourisation of a liquid at `500K` and `atm` pressure is `10kcal mol^(-1)`. What will be change in internal energy of `3mol` of liquid at same temperature?
02:55View SolutionWhat is value of `DeltaU` for reversible isothernal evaporation of `90g` water at `100^(@)C`? Assuming water vapour behaves as an ideal gas, `Delta_(vap. Water)H = 540cal g^(-1)`
03:08View SolutionOne moles of strem is compressed reversibly of water at boiling point `100^(@)C`. The heat of vapourisation of water at `100^(@)C` and `1atm` is `540cal g^(-1)`. Calculate `DeltaU` and `DeltaH`.
03:49View SolutionThe enthalpy combustion of a substance
00:55View SolutionOne litre-atmosphere is approximately equal to
02:04View SolutionCalorific value of fat
02:39View Solution`Xg` of ethanal was subjected to combustion in a bomb calorimeter and the heat produced is `Y J`. Then
03:48View SolutionThe reaction
`SO_(2)(g) +1//2O_(2)(g) rarr SO_(3)(g)` should be02:21View SolutionA hypothetical reaction, `A rarr 2B`, proceeds via following sequence of steps
`{:(ArarrC,,DeltaH = q_(1),,,),(CrarrD,,DeltaH = q_(2),,,),((1)/(2)D rarrB,,DeltaH = q_(3),,,):}`
The heat of reaction is04:21View SolutionA gas expands from `3 dm^(3)` to `5dm^(3)` against a constant pressure of `3atm`. The work done during the expansion if used to heat `10mol` of water at temperature `290K`. Find the final temperature of water, if the specific heat of water `= 4.18g^(-1)K^(-1)`.
03:12View SolutionThe magnitude of ethalphy changes for reversible adiabatic expansion of a gas from volume `V_(1)` to `V_(2)`(in `L)`is `DeltaH_(1)` and for irreversible adiabatic expansion for the same expansion is `DeltaH_(2)`. Then
when `DeltaU_(1)` and `DeltaU_(2)` are the changes in magnitudes for the internal energy of gas in the two expansions.05:44View Solution`1mol` of a mono-atomic gas is subjected to following cyclic process:
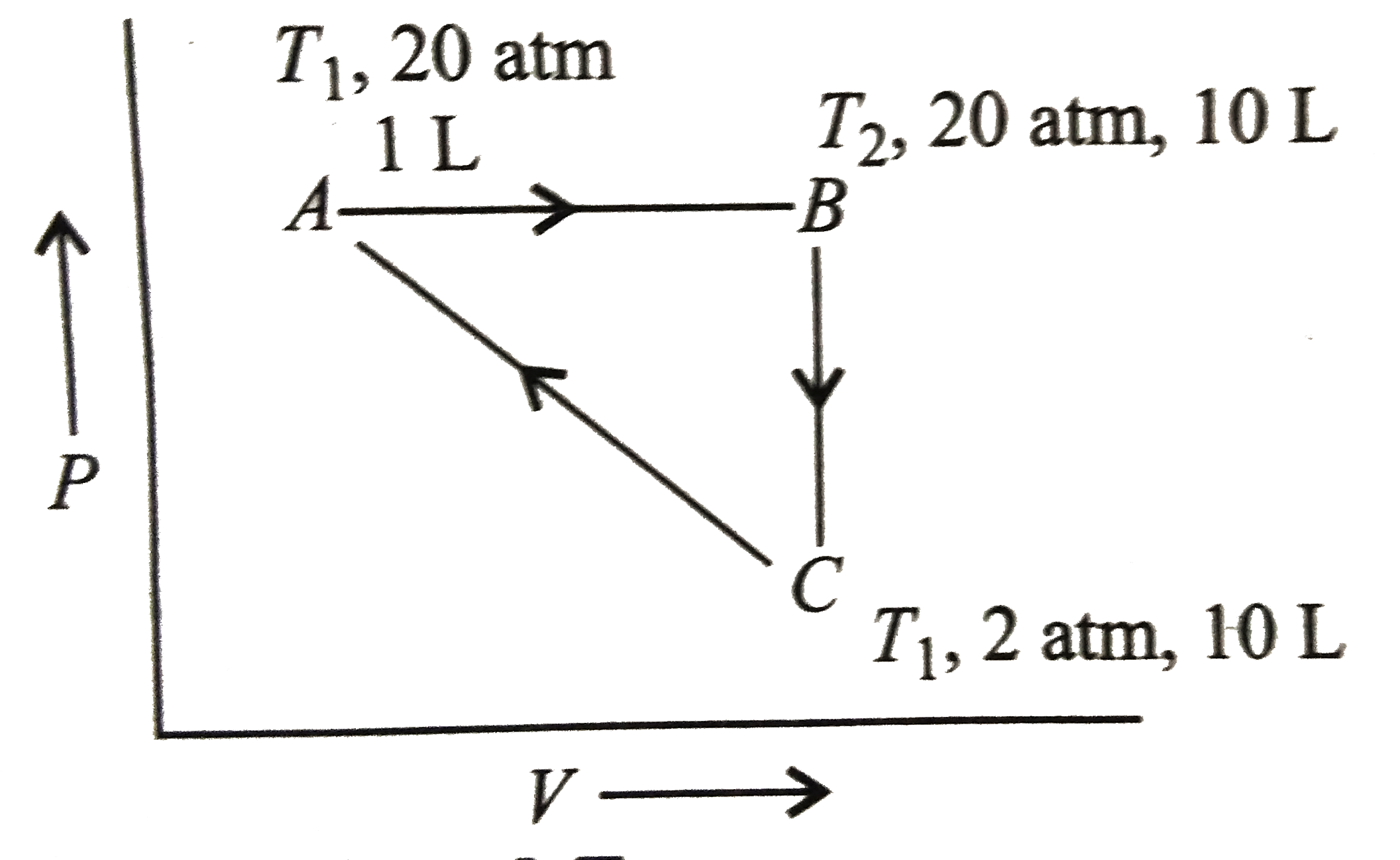
a. Calculate `T_(1)` and `T_(2)`.01:44View SolutionA mono-atomic ideal gas of two moles is taken through a cyclic process starting from `A` as shwon in the figure below.
The volume ratios are `V_(B)//V_(A) = 2` and `V_(D)//V_(A) = 4`. If the temperature `T_(A)` at `A` is `27^(@)C`. Calculate
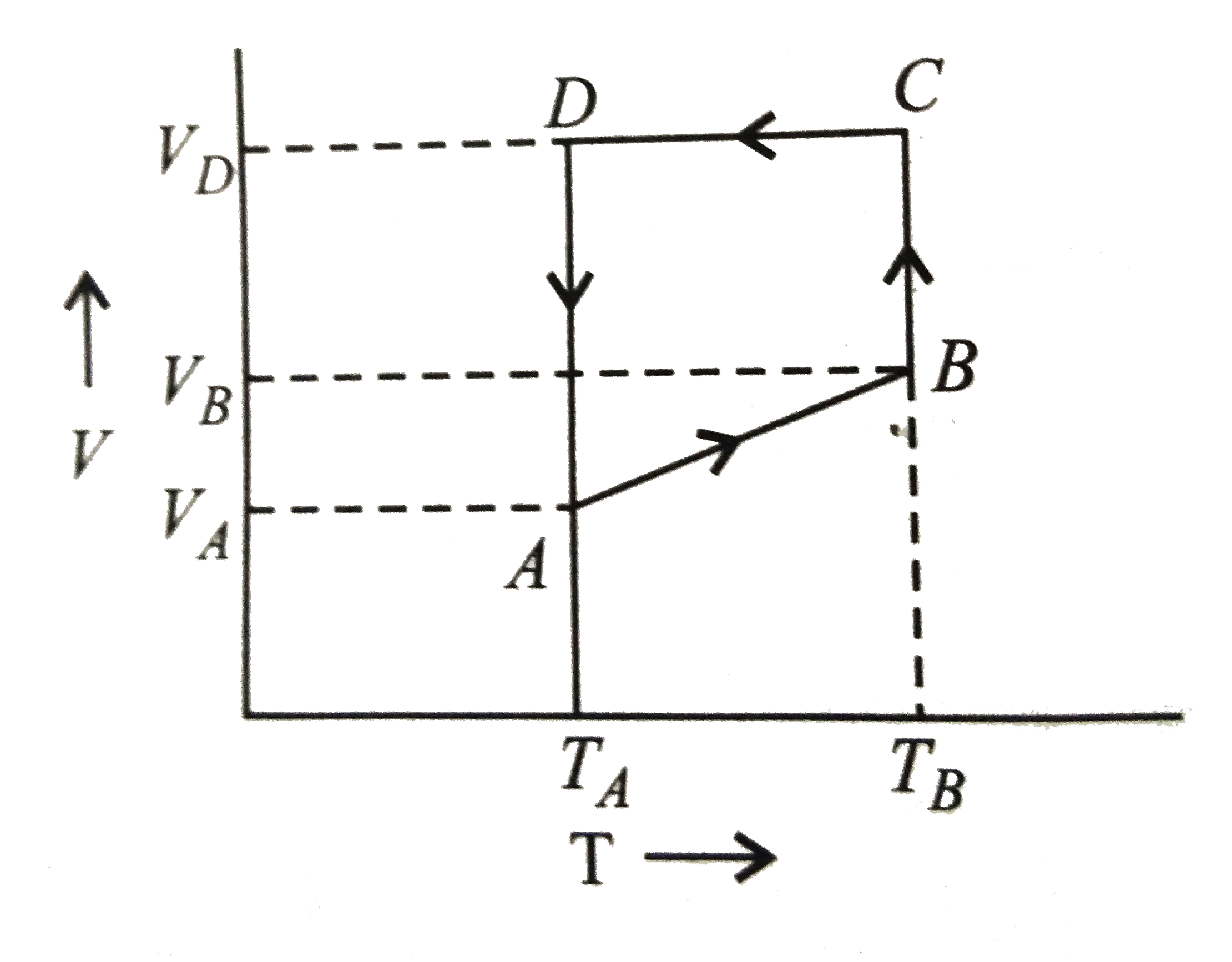
a. The temperature of gas at `B`.
b. Heat absorbed or evolved in each process.
c. Total wrok done in cyclic process.08:17View Solution`4.0 mol` of an ideal gas initially at `1.5atm` and `300K` is heated to `600K` where the pressure is `4.5atm`. Also, `C_(vm) = a+bT, a = 25 J K^(-1)mol^(-1), b = 0.03 J K^(-2) mol^(-1)`. Determine `DeltaU, DeltaH`.
04:57View SolutionThe molar heat capacity for a gas at constant `T` and `P` is
01:06View SolutionA system has internal energy equal to `U_(1), 450J` of heat is taken out of it and `600J` of work is done on it. The final energy of the system will be
01:47View SolutionA lead bullet weighing `18.0g` and travelling at `500 m//s` is embedded in a wooden block of `1.00kg`. If both the nullet and the block were initially at `25.0^(@)C`, what is the final temperature of the block containing bullet? Assume no temperature loss to the surrounding. (Heat capacity of wood `= 0.5 kcal kg^(-1) K^(-1)`, heat capacity of lead `= 0.030 kcal kg^(-1) K^(-1))`
04:04View SolutionA mixture contains `8g He` and `14 g N_(2)` in a vessel at `300K`. How much heat is required to increase the rms speed of these molecules to double their value. Also calculate the final temperatures.
07:44View SolutionAt very low temperatures, heat capacity of a solid is proportional to `T^(3)` and can be written as: `C_(P) = alphaT^(3)` where `alpha = 3xx10^(8)J mol^(-1) K^(-1)`. What is the change in enthalpy when a solid is heated from `0K` to `300K`?
03:27View Solution`50` students sitting in the room of `5 xx 10 xx 3m^(3)` dimensions. The air inside the room is at `27^(@)C` and `1atm` pressure. If each student loses `100` watt heat per second assuming the walls, ceiling floor, and all the material present inside the room is perfectly insulated as well as neglecting loss of air to the outside as the temperature is raised, how much rise in temperature will be noticed in `10min`? Given `C_(P) = (7)/(2)R` for air.
03:46View Solution`50` students sitting in the room of `5 xx 10 xx 3m^(3)` dimensions. The air inside the room is at `27^(@)C` and `1atm` pressure. If each student loses `100` watt heat per second assuming the walls, ceiling floor, and all the material present inside the room is perfectly insulated as well as neglecting loss of air to the outside as the temperature is raised, how much rise in temperature will be noticed in `10min`? Given `C_(P) = (7)/(2)R` for air.
03:46View SolutionA sample of ideal gas `(gamma = 1.4)` is heated at constant pressure. If `140 J` of heat is supplied to gas, find `DeltaU` and `W`.
04:13View SolutionGraph for specific heat at constant volume for a monoatomic gas
01:07View SolutionHeat is supplied to a certain homogeneous sample of amtter, at a uniform rate. Its temperature is plotted against time, as shown in the figure below. Which of the following conclusions can be drawn?
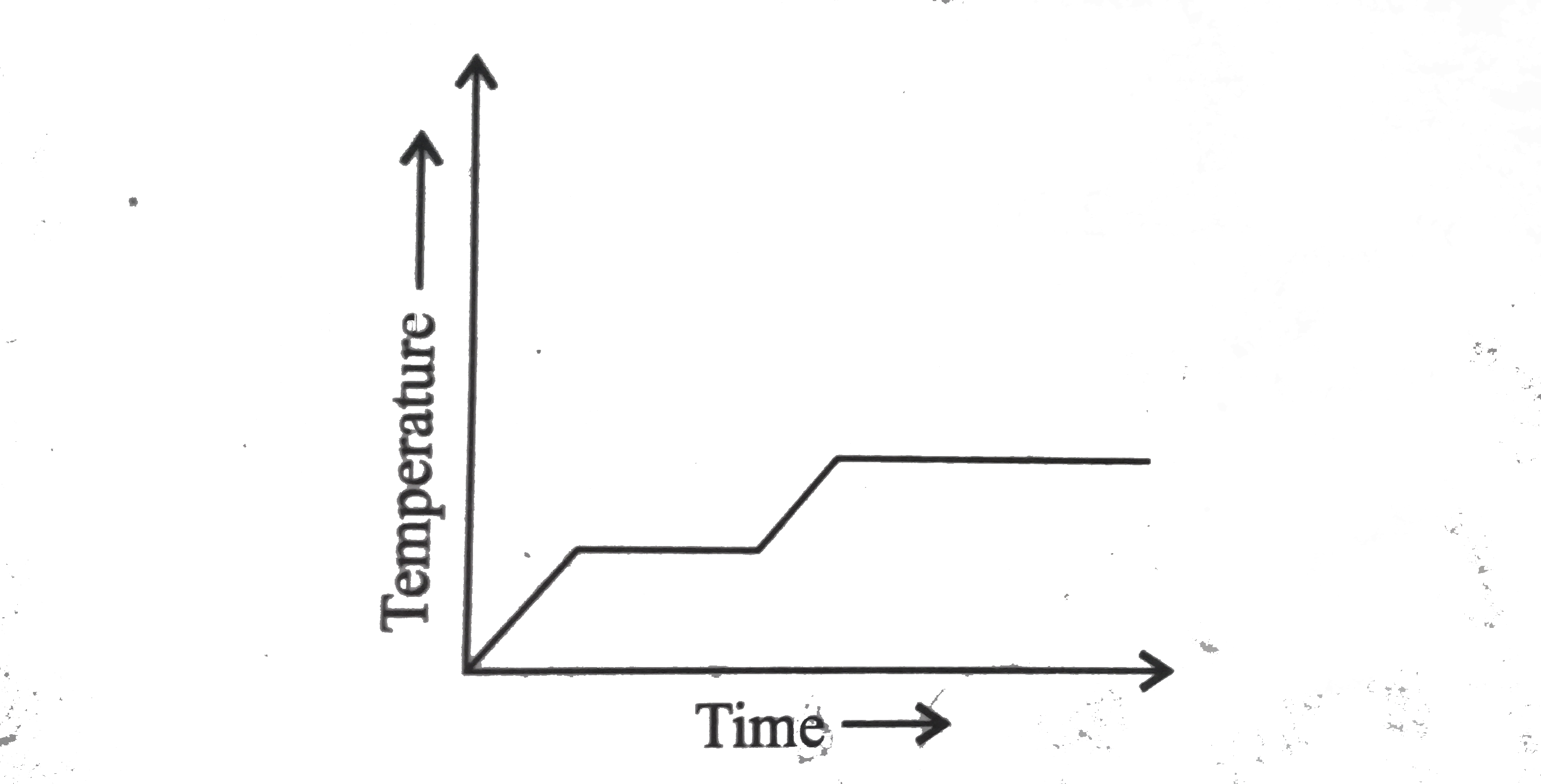 02:00View Solution
02:00View SolutionSpecific heat of constant pressure of a diatomic gas having molar mass `M` is approximately equal to
01:50View SolutionThe following is not an endothermic reactions:
03:11View SolutionFor the reaction
`N_(2)(g) + 3H_(2)(g) rarr 2NH_(2)(g)`
Which of the following is correct?02:00View Solution`100mL` of a liquid is contained in an insulated container at a pressure of 1bar. The pressure is steeply increased to `100`bar. The volume of the liquid is decreased by `1mL` at this constant pressure. Find `DeltaH` and `DeltaU`.
02:46View Solution`14 g` oxygen at `0^(@)C` and `10 atm` is subjected to reversible adiabatic expansion to a pressure of `1atm`. Calculate the work done in
a. Litre atmosphere.
b. Calorie (given, `C_(P)//C_(V) = 1.4)`.06:22View SolutionWhen a polyatomic gas undergoes an adiabatic process, its tempertaure and volume are related by the equation `TV^(n) =` constant, the value of `n`will be
01:50View SolutionA mono-atomic gas `X` and an diatomic gas `gamma` both initially at the same temperature and pressure are compressed adiabatically from a volume `V` to `V//2`. Which gas will be at higher temperature?
01:43View SolutionA flask of `1L` having `NH_(3)(g)` at `2.0atm` and `200K` is connected with the another flask of volume `800 mL` having `HCI(g)` at `8atm` and `200K` through a narrow tube of negligible volume. The two gases react to form `NH_(4)(CI(s)` with evolution of `43kJ mol^(-1)` heat. if heat capacity of `HCI(g)` at constant volume is `20 JK^(-1) mol^(-1)` and neglecting heat capacity of flask, `NH_(4)CI`, and volume of solid `NH_(4)CI` formed, calculated in the flasks, produced, final temperature, and final pressure in the flasks. (Assume `R = 0.08 L atm K^(-1) mol^(-1))`
07:21View SolutionA gas originally at `1.10atm` and `298K` underwent a reversible adiabatic expansion to `1.00atm` and `287K`. What is the molar heat capacity of the gas?
01:59View SolutionOne mol of an ideal diatomic gas underwent an adiabatic expansion form `298K, 15.00atm`, and `5.25L` to `2.5atm` against a constant external pressure of `1.00atm`. What is the final temperature of the system?
04:07View SolutionA sample of organ gas at `1atm` pressure and `27^(@)C` expands reversibly and adiabatically from `1.25 dm^(3)` to `2.50 dm^(3)`. Calculate the enthalpy change in this process. `C_(vm)` for orgon is `12.48J K^(-1) mol^(-1)`.
03:53View Solution
Solved Examples questions and complete solutions for chapter THERMODYNAMICS of CENGAGE CHEMISTRY (ENGLISH) of Class 11
All Exercises from CENGAGE CHEMISTRY Class 11 CHEMISTRY THERMODYNAMICS
- Archives (Assertion-Reasoning)
- Archives (Fill In The Blanks)
- Archives (Interger)
- Archives (Multiple Correct)
- Archives (Single Correct)
- Archives (Subjective)
- Archives (True/False)
- Ex 6.1
- Ex 6.2
- Ex 6.3
- Ex 6.4
- Ex 6.5
- Exercise
- Exercises (Assertion-Reasoning)
- Exercises (Fill In The Blanks)
- Exercises (Interger)
- Exercises (Linked Comprehension)
- Exercises (Multiple Correct)
- Exercises (Single Correct)
- Exercises (Subjective)
- Exercises (True/False)
- Multiple correct Answer Type
- Paragraph for Problem
- Solved Examples
- True/False Type
