Complete Solutions to Subjective of chapter TRAVELLING WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TRAVELLING WAVES |
| CENGAGE PHYSICS | Subjective |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
A 100 Hz sinusoidal wave is travelling in the positive x-direction along a string with a linear mass density of `3.5xx10^(3) kg//m` and a tension of 35 N. time t=0, the point x=0 has maximum displacement in the positive y-direction. Next, when this point has zero displacement the slope (iii) the expression which represents the displacement of string as a function of x (in metres) and t (in seconds).
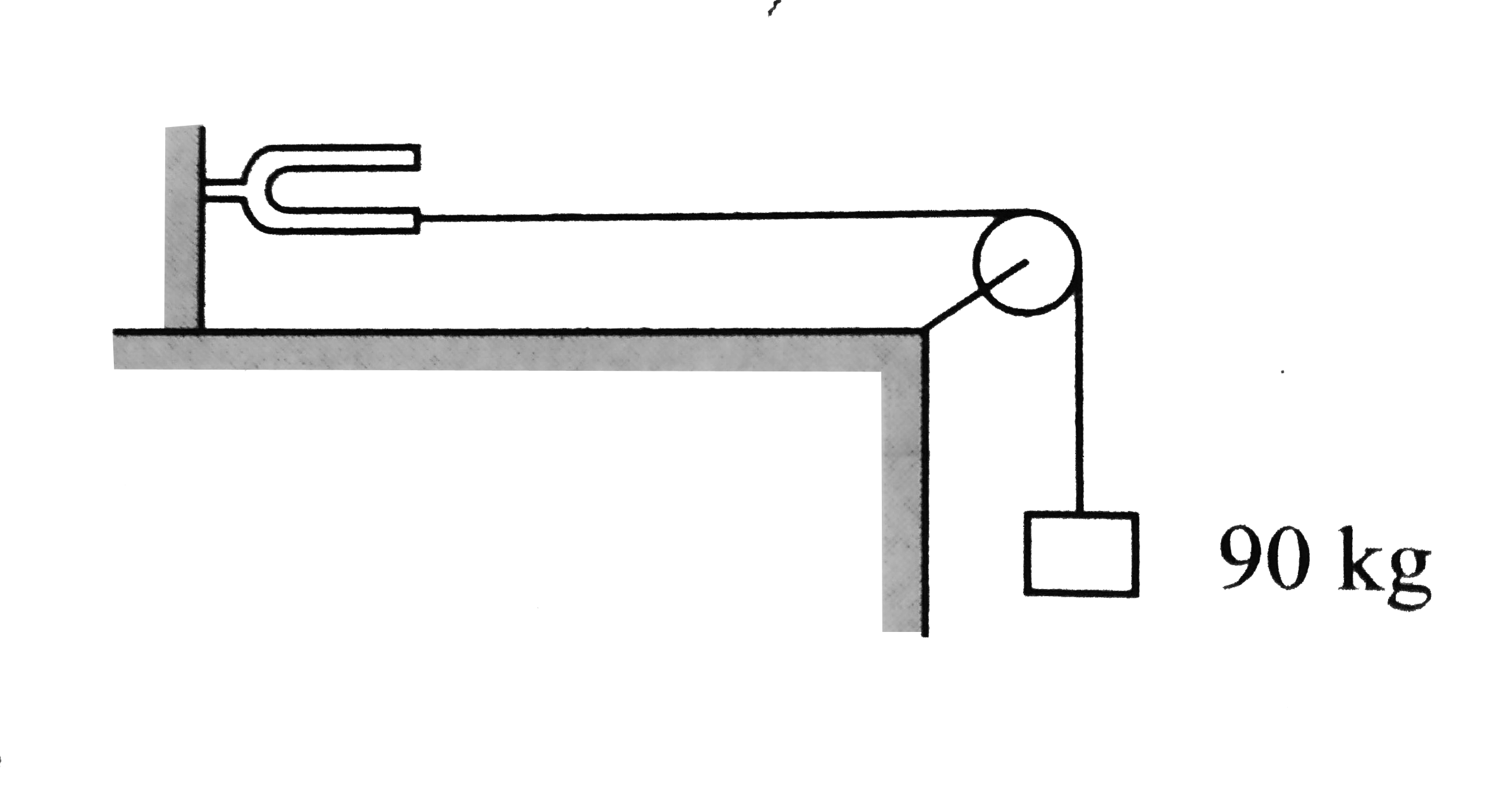
View SolutionOne end of a long string of linear mass density `10^(-2) kg m^(-1)` is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
View SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View SolutionA harmonic wave is travelling in a stationary medium whose equation of this wave w.r.t. a frame which is moving along -ve x-axis with a constant speed v w.r.t. stationary medium. Also, find speed of wave in moving frame.
View SolutionA plane undamped harmonic wave progates in a medium. Find the mean space density of energy becomes equal to `W_(0)` at an instant `t=t(0)+T//6`, where `t_(0)` is the instant when amplitude is maximum at this location and T is the time period of oscillation.
View SolutionA steel wire has a mass of `50 g//m` and is under tension 450N.
(a) Find the maximum average power that can be carried by the transverse wave in the wire if the amplitude not to exceed 20% of the wavelength. (b) The change in maximum average power if the mass per unit length of the wire is doubled. `(Use pi^(2)~=10.)`
View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
`y=y_0e^-(t/T-x/lamda)^2`
where `y_0=4mm, T=1.0s and lamda=4cm`. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.
View SolutionA travelling wave pulse is given by `y = (10)/(5 + (x + 2t)^(2))`
Here, `x and y` are in meter and `t` in second. In which direction and with what velocity is the pulse propagation. What is the ampitude of pulse?
View SolutionA 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of `19.2xx10^-3 kgm^-1`. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of `2.0ms^-2. Take g=10 ms^-2`.
View SolutionThe speed of a transverse wave going on a wire having a length 50 cm and maas 5.0 g is `80ms^(-1)` The area of cross section of the wire is `1.0mm.^2` and its Young modulus is `16 xx 10^(11) N m^(-2).` Find the extension of the wire over its natural lenth.
View SolutionTwo blocks each having a mass of 3.2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB . The linear mass density of the wire AB is `10 gm^-1` and that of CD is `8 g m^-1.` Find the speed of a transverse wave pulse produced in AB and in CD.
View SolutionA transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
View Solutionshows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.

(a) write down the equation of the curve. (b) find the angle `theta` made by the tangent at point P with the x-axis. (c ) If the particle at P has a velocity `v_(p) m//s`, in the negative y-direction, as shown in figure, then determine the speed and direction of the wave. (d) find the frequency of the wave. (e) find the displacement equation of the particle at the origin as a function of time. (f) find the displacement equation of the wave.
View SolutionFigure shows two snapshots of medium particle within a time interval of `1/60` s. find the possible time periods of the wave

View SolutionThe equetion of a progressive wave travelling along a string is given by
`y=10 sinpi(0.01x-2.00t)`
where x and y are in centimetres and t in seconds. Find the (a) velocity of a particle at x=2 m and `t=5//6` s. (b) acceleration of a particle at x=1 m and `t=1//4` s. also find the velocity amplitude and acceleration amplitude for the wave.
View SolutionA travelling wave is given by
`y=(0.8)/((3x^(2)+24xt+48t^(2)+4))`
where `x` and `y` are in metres and `t` is in seconds. Find the velocity in `m//s`.
View Solution
Subjective questions and complete solutions for chapter TRAVELLING WAVES of CENGAGE PHYSICS (HINGLISH) of Class 11