Complete Solutions to Single Correct of chapter TRAVELLING WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TRAVELLING WAVES |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
The speed of a wave in a certain medium is `960 m//s`. If 3600 waves pass over a certain point of the medium in 1 min, the wavelength is
View SolutionA simple harmonic progressive wave is representive by the equation `y=8 sin 2pi (0.1x -2t)` where x and y are in centimetres and t is in seconds. At any instant the phase difference between two particle separted by 2.0 cm along the x-direction is
View SolutionThe equation of a transverse travelling on a rope is given by `y=10sinpi (0.01x-2.00t)` where y and x are in cm and t in seconds. The maximum transverse speed of a particle in the rope is about
View SolutionA wave is represented by the equetion
`y=7 sin(7pi t-0.04pix+(pi)/(3))`
x is in metres and t is in seconds. The speed of the wave is
View SolutionThe path difference between the two waves
`y_(1)=a_(1) sin(omega t-(2pi x)/(lambda)) and y(2)=a_(2) cos(omega t-(2pi x)/(lambda)+phi)` is
View SolutionA travelling wave is described by the equation `y = y_(0) sin ((ft - (x)/lambda))`. The maximum particle velocity is equal to four times the wave velocity if
View SolutionThe equetion of a wave travelling on a string is
`y pi 4 sin(pi)/(2)(8t-(x)/(8))`
if x and y are in centimetres, then velocity of waves is
View SolutionIf `x pi asin[omega pi pi //6]` and x' acosomegat, then what is the phase difference between the two waves?
View SolutionA simple harmonic wave is represent by the relation
`y(x,t)=a_(0) sin 2pi(vt-(x)/(lambda))`
if the maximum particle velocity is three times the wave velocity, the wavelength `lambda` of the wave is
View SolutionThe equation of a travelling wave is
`y60 cos(1800t-6x)`
where y is in microns, t in seconds and x in metres. The ratio of maximum particle velocity to velocity of wave propagation is
View SolutionThe equation of a progressive wave is
`y=0.02sin2pi[(t)/(0.01)-(x)/(0.30)]`
here x and y are in metres and t is in seconds. The velocity of propagation of the wave is
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by
`y =(1)/(1 + x^(2))`at `t = 0` and `y =(1)/(1 +(x - 1)^(2))` at `t =2s`
where, `x` and `y` are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionIn a medium in which a transverse prograssive wave is travelling, the phase difference between two points with a separation of 1.25 cm is `(pi//4). If the frequancy of wave is 1000 Hz. Its velocity will be
View SolutionA plane sound wave is travelling in a medium. In reference to a frame A, its equation is y=a cos `(omegat-kx)`. Which refrence to frame B, moving with a constant velocity v in the direction of propagation of the wave, equation of the wave will be
View SolutionSmall amplitude progressive wave in a stretched string has a speed of `100 cm//s` and frequency 100 Hz. The phase difference between two points 2.75 cm apart on the string in radians, is
View SolutionThe linear density of a vibrating string is `10^(-4) kg//m`. A transverse wave is propagating on the string, which is described by the equation `y=0.02 sin (x+30t)`, where x and y are in metres and time t in seconds. Then tension in the string is
View SolutionTwo blocks of masses 40 kg and 20 kg are connected by a wire that has a linear mass density of `1 g//m`. These blocks are being pulled across horizontal frictionless floor by horizontal force F that is applied to 20 kg block. A transverse wave travels on the wave between the blocks with a speed of `400 m//s` (relative to the wire). the lmass of the wire is negligible compared to the mass of the blocks. the magnitude of F is
View SolutionAt t=0, the shape of a travelling pulse is given by
`y(x,0)=(4xx10^(-3))/(8-(x)^(-2)`
where x and y are in metres. The wave function for the travelling pulse if the velocity of propagation is `5 m//s` in the x direction is given by
View SolutionThe amplitude of a wave represented by displacement equation `y=(1)/(sqrta)sinomega+-(1)/(sqrtb)cosomegat` will be
View Solutiontwo particle of medium disturbed by the wave propagation are at `x_(1)=0 and x_(2)=1 cm`. The respective displacement (in cm) of the particles can be given by the equation:
`y_(1)=2 sin 3pi t, y_(2) sin (3pi t-pi//8)` the wave velocity is
View SolutionThe displacement vs time graph for two waves A and B which travel along the same string arre shown in the figure. Their intensity ratio `I_(A)|I_(B)` is

View SolutionAt t=0,a transverse wave pulse travelling in the positive x direction with a speed of `2 m//s` in a wire is described by the function `y=6//x^(2)` given that `x!=0`. Transverse velocity of a particle at x=2 m and t= 2 s is
View SolutionWave pulse on a string shown in figure is moving to the right without changing shape. Cosider two particle at positions `x_(1)=1.5 m and x_(2)=2.5 m`. Their transverse velocities at the moment shown in figure are along direction

View SolutionA wave pulse is generated in a string that lies along `x-`axis. At the points `A` and `B`, as shown in figure, if `R_(A)` and `R_(B)` are ratio of magnitudes of wave speed to the particle speed, then
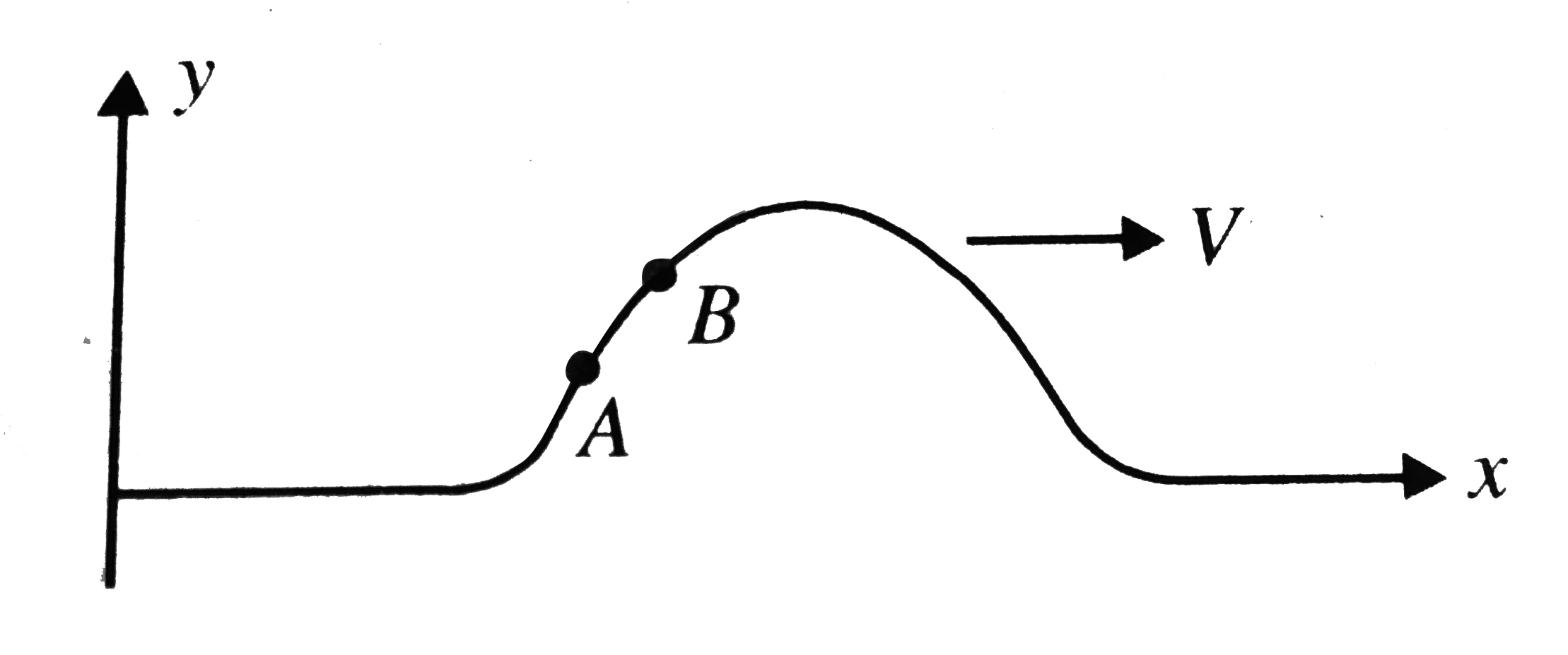
View SolutionSinusoidal waves `5.00 cm ` in amplitude are to be transmitted along a string having a linear mass density equal to `4.00xx10^-2kg//m`. If the source can deliver a maximum power of `90W` and the string is under a tension of `100N`, then the highest frequency at which the source can operate is (take `pi^2=10`)
View SolutionAdjoining figure shows the snapshot of two waves A and B at any time t. the equation for A is `y=Asin (kx-omegat-phi)`, and for B it is `y=A sin (kx-omega t)`. It is clearly shown in the figure that wave A is ahead of B by a distance `phi//k`.

View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by `2.0 cm`. the motion of bar is continuous and is repeated regularly `125` times per second. If klthe distance between adjacent wave crests is observed to be `15.6 cm` and the wave is moving along positive `x-`direction, and at `t=0` the element of the string at `x=0` is at mean position `y =0` and is moving downward, the equation of the wave is best described by
View SolutionIf the maximum speed of a particle on a travelling wave is `v_(0)`, then find the speed of a particle when the displacement is half of the maximum value.
View SolutionA sinusoidal wave is generated by moving the end of a string up and down, periodically. The generated must apply the energy has ………..x and least power when the end of the string attached to generated to generated has ………..Y. the most suitable option which correctly fills blanks X and Y, is
View SolutionA point source of sound is placed in a non-absorbing medium two points A and B are at the distance of 1 m and 2 m, respectively, from the source. The ratio of amplitudes of waves at A to B is
View SolutionTwo canoes are 10 m apart on a lake. Each bobs up and down with a period of 4.0 s. when one canoe is at its highest point, the other canoe is at its lowest point. Both canoes are always within a single cycle of the waves determine the speed of the wave.
View SolutionThe mathmaticaly form of three travelling waves are given by
`Y_(1)=(2 cm) sin (3x-6t)`
`Y_(2)=(3 cm) sin (4x-12t)`
And `Y_(3)=94 cm) sin(5x-11t)`
of these waves,
View SolutionA transverse wave on a string travelling along + ve x-axis has been shown in the figure below:
The mathmetical form of the shown wave is
`y=(3.0 cm) sin [2pixx0.1t-(2pi)/(100)x]`
where t is in seconds and x is in centimetres. Find the total distance travelled by the particle at (1) in 10 min 15 s. measured from the instant shown in the figure and direction of its motion at the end of this time.
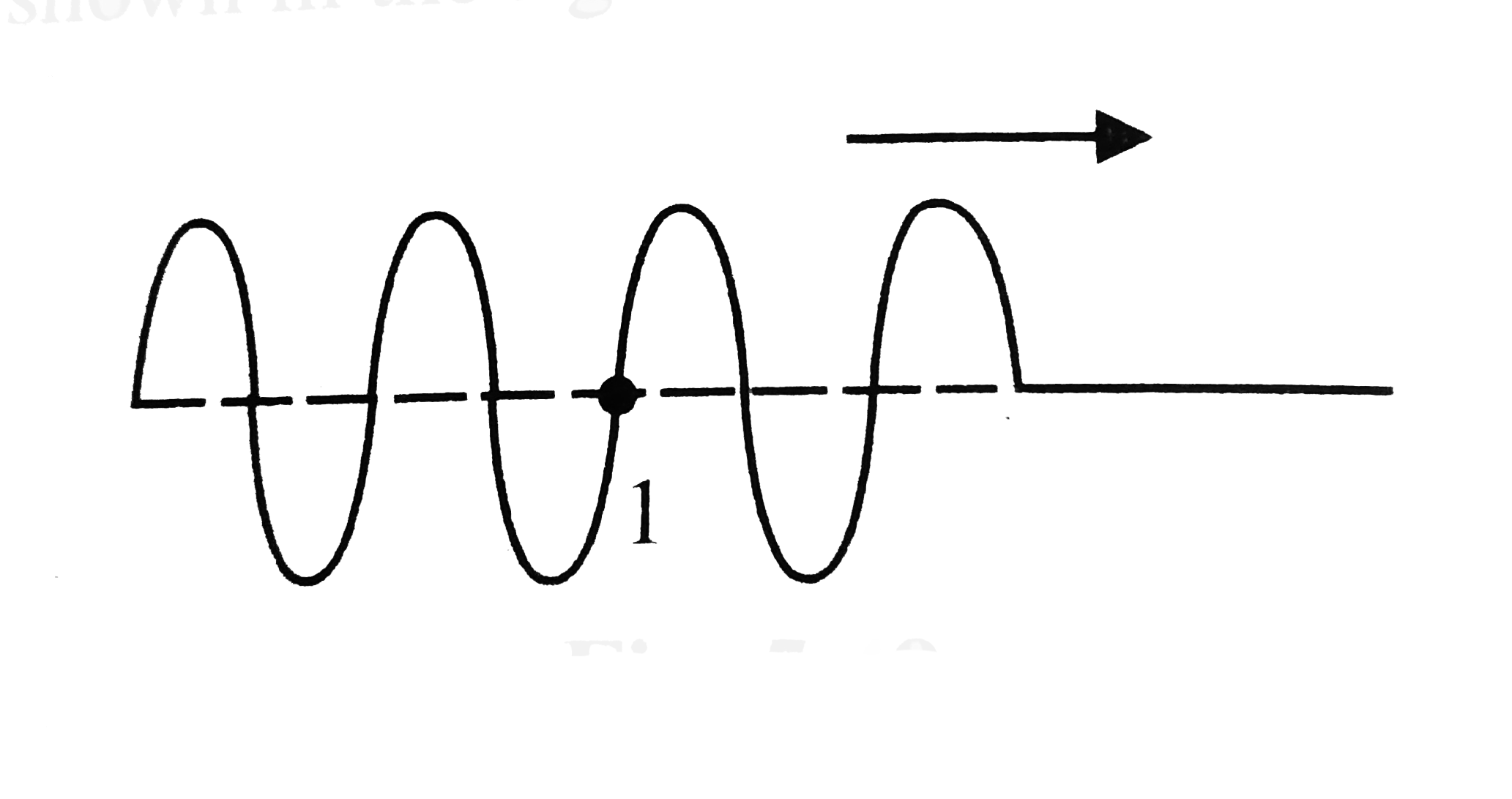
View SolutionA water surfer is moving at a speed of `15 m//s`. When he is surfing in the direction of wave, he swing upwards every 0.8 s because of wave crests. While surfing in opposite direction to that of wave motion, he swings upwards every 0.6 s. determine the wavelength of transverse component of the water wave.
View SolutionA transverse wave on a string has an amplitude of 0.2 m and a frequency of 175 Hz. Consider a particle of the string at x=0. it begins with a displacement y=0, at t=0, according to equation `y=0.2 sin (kx+-omegat)`. How much time passed between the first two instant when this particle has a displacement of y=0.1 m?
View SolutionIf a wave is going from one medium to another, then
View SolutionAt t=0,a transverse wave pulse travelling in the positive x direction with a speed of `2 m//s` in a wire is described by the function `y=6//x^(2)` given that `x!=0`. Transverse velocity of a particle at x=2 m and t= 2 s is
View SolutionA harmonic wave has been set up on a very long string which travels along the length of string. The wave has frequency of 50 Hz. Amplitude 1 cm and wavelength 0.5 m. for the above described wave.
Statement (i): time taken by a point on the string to travel a distance of 8 m along the length of strime is 0.32 s.
Statement (ii): time taken by a point in the string to travel a distance of 8m, once the wave has reached at that point and sets it into motion is 0.32 s.
View SolutionA point source of sound is placed in a non-absorbing medium two points A and B are at the distance of 1 m and 2 m, respectively, from the source. The ratio of amplitudes of waves at A to B is
View SolutionA wave is represented by the equetion
`y=y_(0)sin [10pix-15pit+(pi//3)]`
where x is in metres and t in seconds. The equation represent a travelling wave:
View SolutionA progressive wave is given by
`y=3 sin 2pi [(t//0.04)-(x//0.01)]`
where x, y are in cm and t in s. the frequency of wave and maximum accelration will be:
View SolutionA transverse waves is travelling in a string. Study following statement.
(i) Equation of the wave is equal to the shape of the string at an instant t. (ii) Equation of thhe wave is general equation for displacement of a particle of the string (iii) Equation of the wave must be sinusoidal equation (iv) Equation of the wave is an equation for displacement of the particle at one end only.correct statement are
View SolutionThe equuation of a wave is given by
`y=0.5 sin (100 t+25x)`
The ratio of maximum particle velolcity to wave velocity is:
View SolutionThe two waves are represented by
`y_(1) 10^(-6) sin(100t (x)/(50) 0.5)m`
`Y_(2) 10^(-2) cos(100t (x)/(50))m`
where x is ihn metres and t in seconds. The phase difference between the waves is approximately:
View SolutionWhich of the following is not true for the progressive wave
`ypi4sin2pi((t)/(0.02)-(x)/(100))`
where x and y are in cm and t in seconds.
View SolutionThe amplitude of a wave disturbance propagating along positive X-axis is given by `=1/(1+x^(2))` at t=0 and `y=1/[1+(x-2)^(2)]` at t=4 s where x and y are in metre. The shape of wave diturbance does not change with time. The velocity of the wave is
View SolutionConsider a wave rpresented by `y= a cos^(2) (omega t-kx)` where symbols have their usual meanings. This wave has
View SolutionAt t=0, a transverse wave pulse in a wire is described by the function `y=6//(x^(2)-3)` where x and y are in metres. The function y(x,t) that describes this wave equation if it is travelling in the positive x direction with a speed of `4.5 m//s` is
View SolutionA stretched rope having linear mass density `5xx10^(-2)kg//m` is under a tension of `80 N`. the power that has to be supoplied to the rope to generate harmonic waves at a frequency of `60 Hz` and an amplitude of `(2sqrt2)/(15pi)m` is
View SolutionAstring of length 2L, obeying hooke's law, is stretched so that its extension is L. the sped of the tansverse wave travelling on the string is v. if the sting is further on the string will be
View SolutionA sinusoidal wave travelling in the positive direction on a stretched string has amplitude `2.0 cm`, wavelength `1.0 m` and velocity `5.0 m//s`. At `x = 0` and ` t= 0` it is given that `y = 0` and `(dely)/(delt) lt 0`. Find the wave function `y (x, t)`.
View SolutionFor the wave shown in figure, write the equation of this wave if its position is shown at `t= 0`. Speed of wave is `v = 300m//s`.
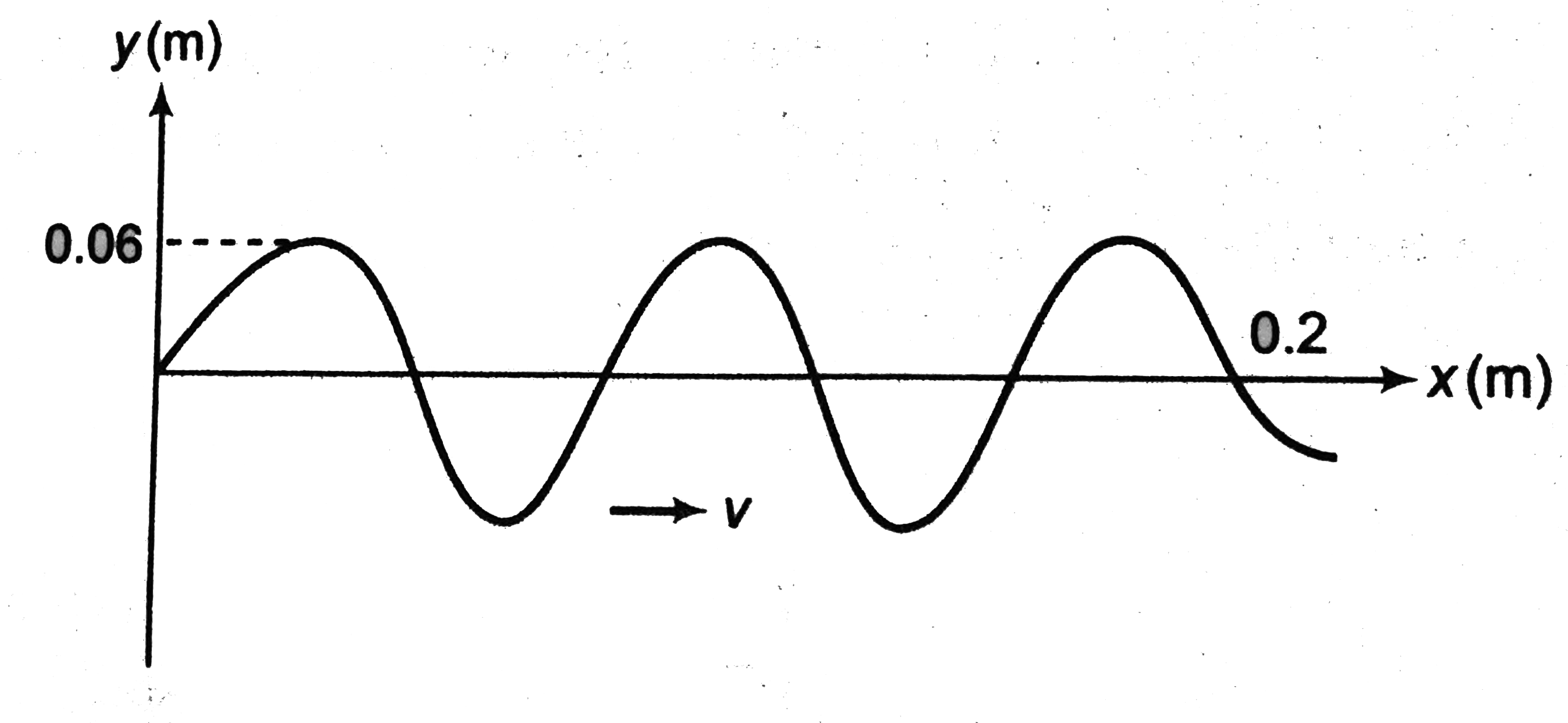
View Solution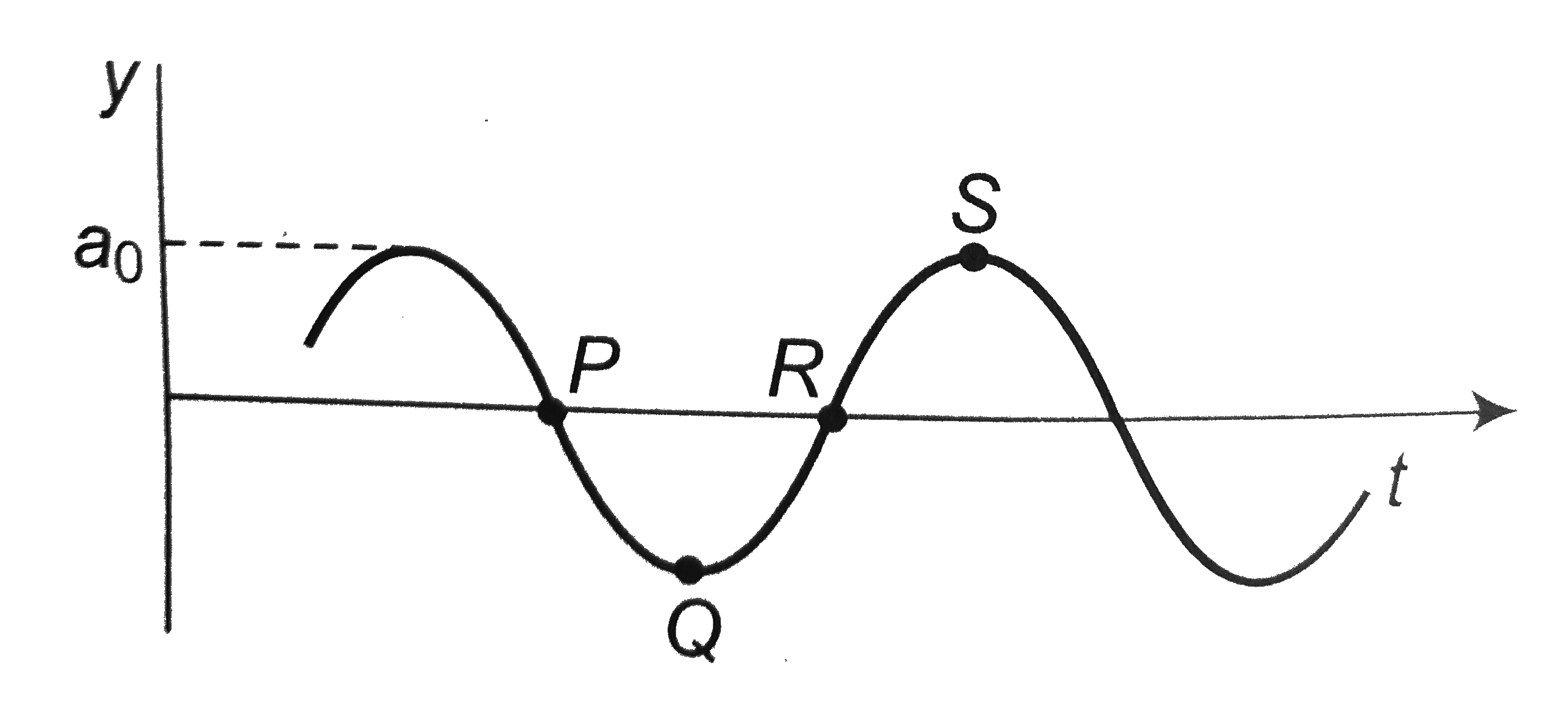
A wave motion has the function `y=a_0sin(omegat-kx)`. The graph in figure shows how the displacement y at a fixed point varies with time t. Which one of the labelled points Shows a displacement equal to that at the position `x=(pi)/(2k)` at time `t=0`?
View SolutionThe prong of an electrically operated tuning fork is connected to a long string of `mu=1 kg//m` and tension 25 N, the maximum velocity of the prong is `1 cm//s`, then the average power needed to drive the prong is

View SolutionThe figure below is a representation of a simple harmonic progressive in the negative X-axis, at a given instant. The direction of the velocity of the particle at stage P in the figure is best represent by the arrow.
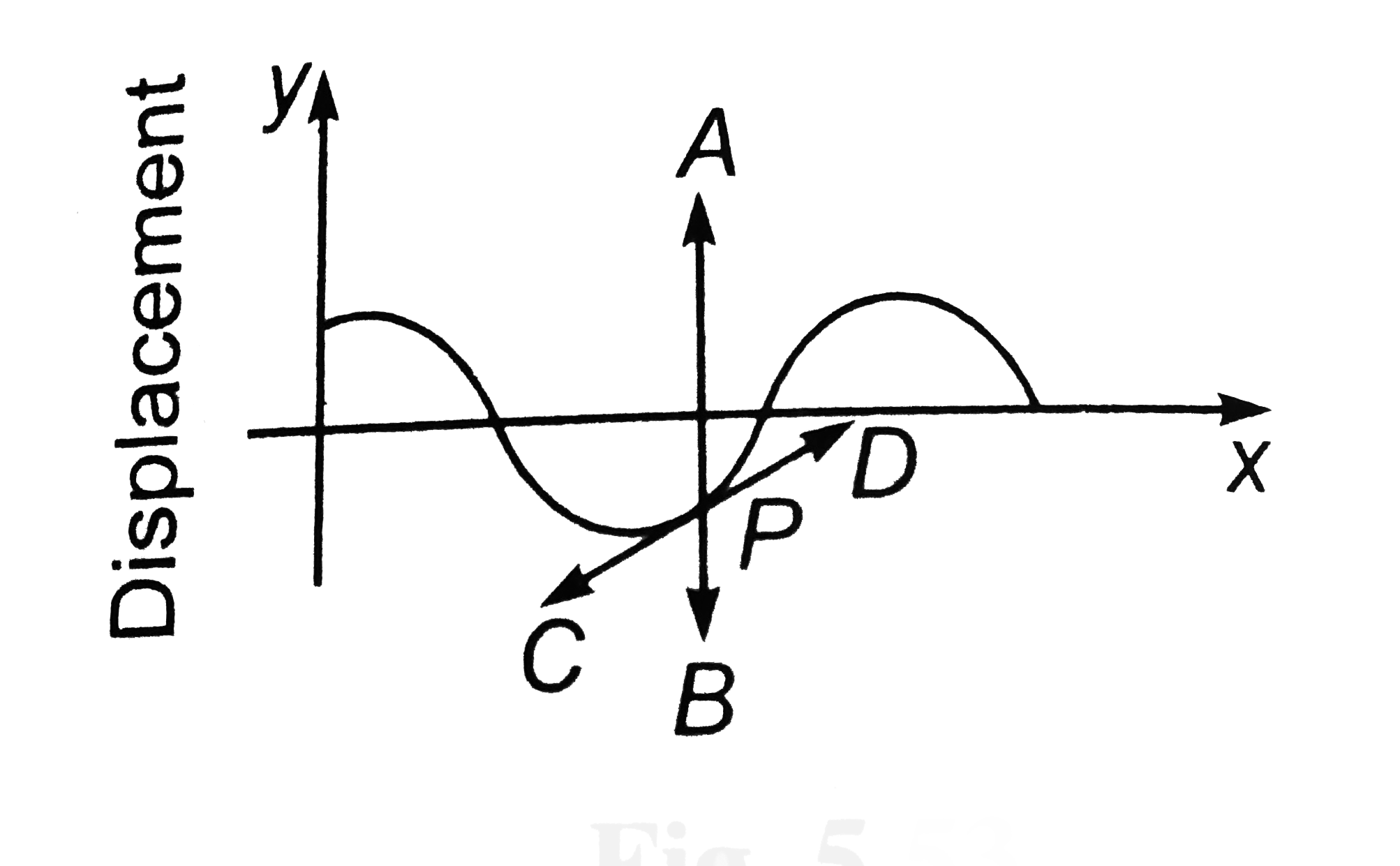
View SolutionThe graph shows a wave at t=0 travelling to the right with a velocity of `4 m//s`. The equation that best represents the wave is

View SolutionA circular loop of rope of length L rotates with uniform angular velocity `omega` about an axis through its centre on a horizontal smooth platform. Velocity of pulse (with resppect to rope ) produce due to slight radiul displacement is given by

View SolutionIn the above question, if the motion of the pulse and rotation of the loop, both are in same direction then the velocity of the pulse w.r.t. to ground will be:
View SolutionIn the above question,if both are in opposite direction. Then the velocity of the pulse w.r.t. to groun will be:
View SolutionGraph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If `omega_(1),omega_(2) and omega_(3)` are their angular frequencies, respectively, then:

View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View Solution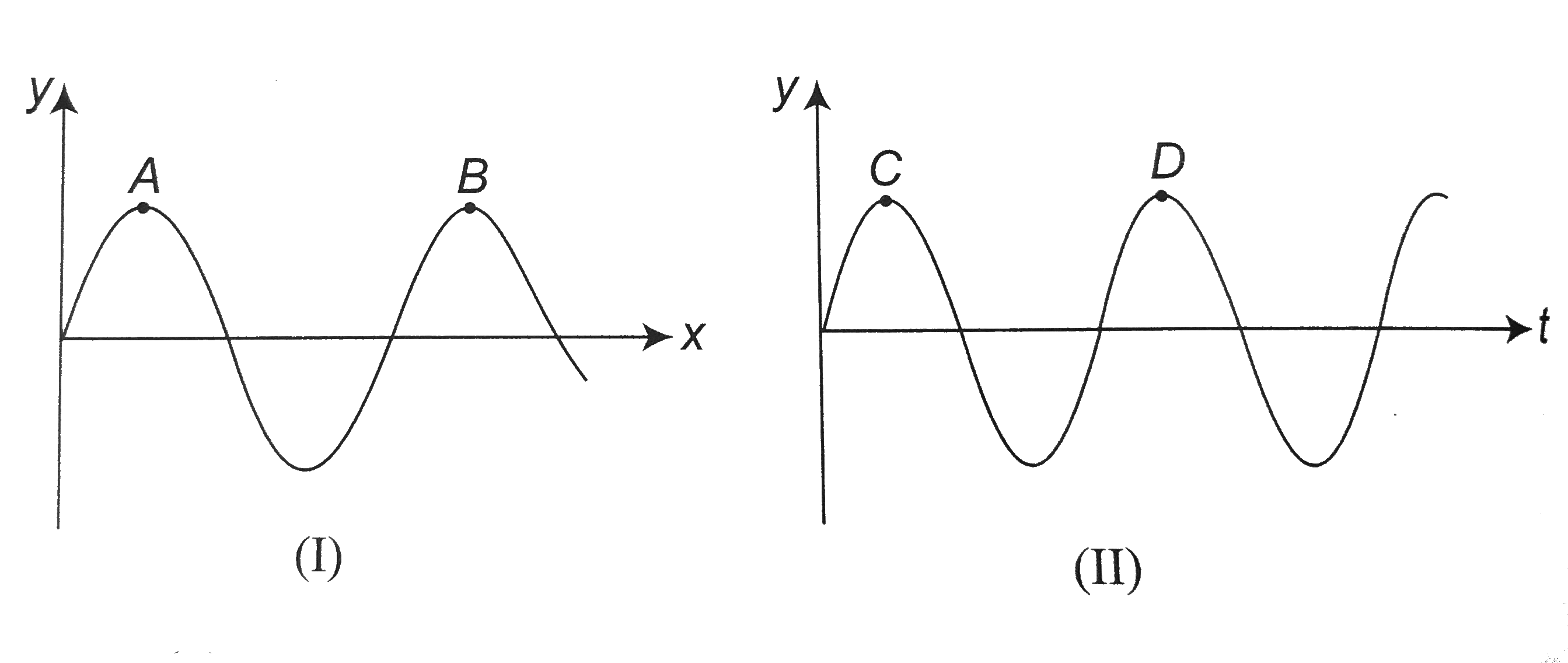
The same progressive wave is represented by two graphs I and II. Graph I shows how the displacement `y` varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curves represents:
View Solution
Single Correct questions and complete solutions for chapter TRAVELLING WAVES of CENGAGE PHYSICS (HINGLISH) of Class 11