Complete Solutions to Comprehension of chapter TRAVELLING WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TRAVELLING WAVES |
| CENGAGE PHYSICS | Comprehension |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
The figure represents two snaps of a travelling wave on a string of mass per unit length `mu=0.25 kg//m`. The first snap is taken at t=0 and the second is taken at `t=0.05 s`.
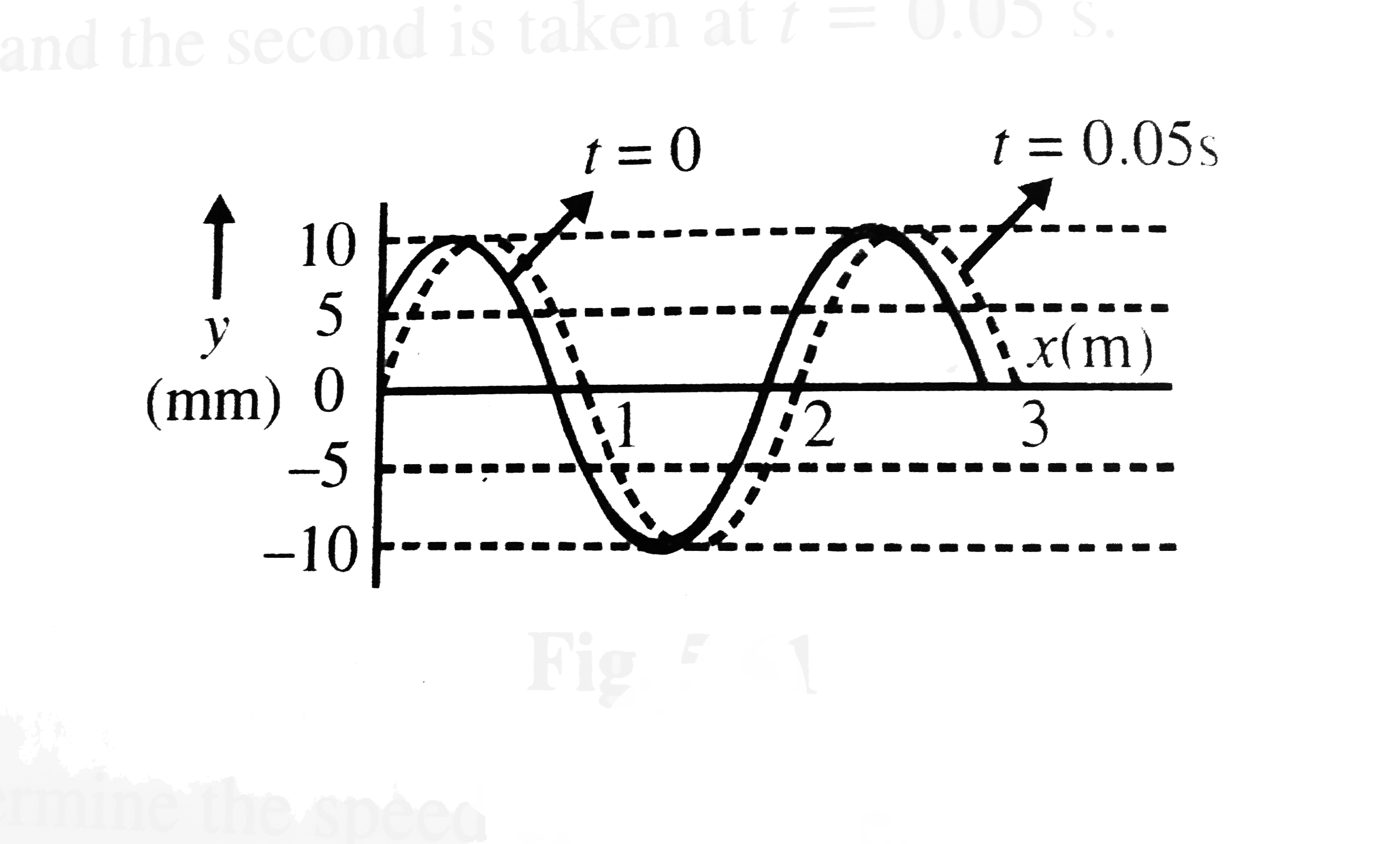
Determine the speed of the wave.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length `mu=0.25 kg//m`. The first snap is taken at t=0 and the second is taken at `t=0.05 s`.
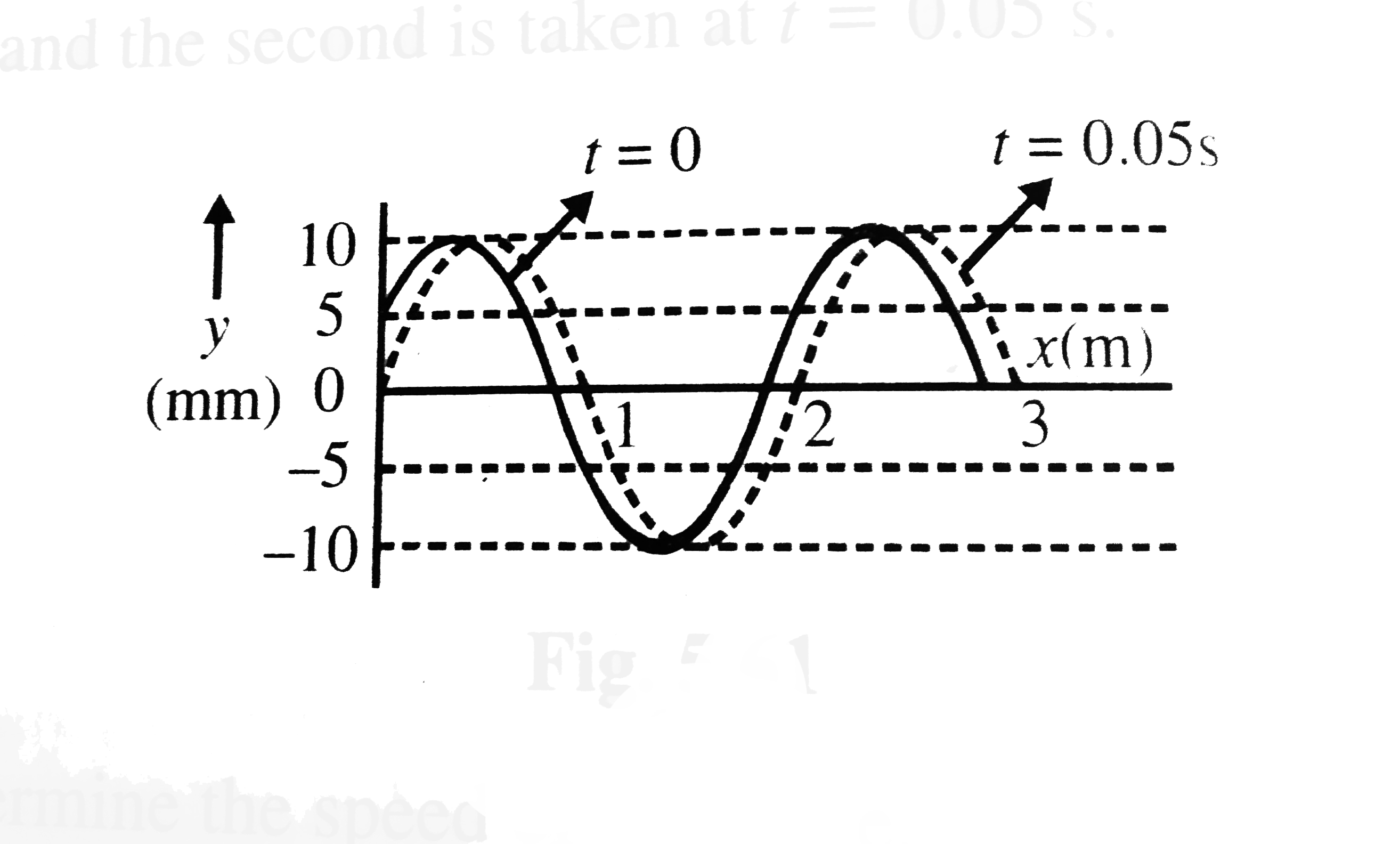
Determine the frequency of the wave.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length `mu=0.25 kg//m`. The first snap is taken at t=0 and the second is taken at `t=0.05 s`.
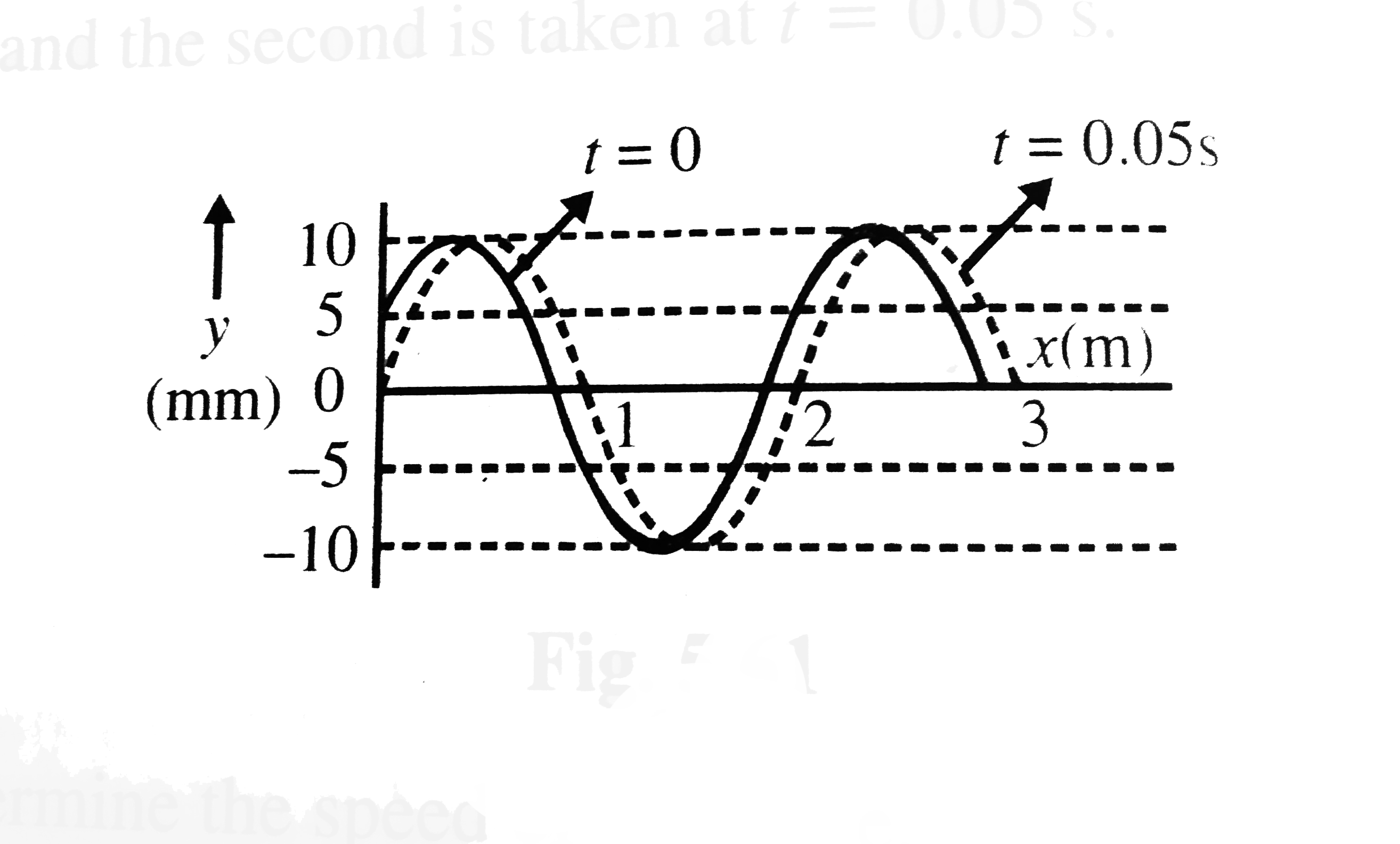
Determine the maximum speed of the particle.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length `mu=0.25 kg//m`. The first snap is taken at t=0 and the second is taken at `t=0.05 s`.

Determine the tension in the string.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length `mu=0.25 kg//m`. The first snap is taken at t=0 and the second is taken at `t=0.05 s`.
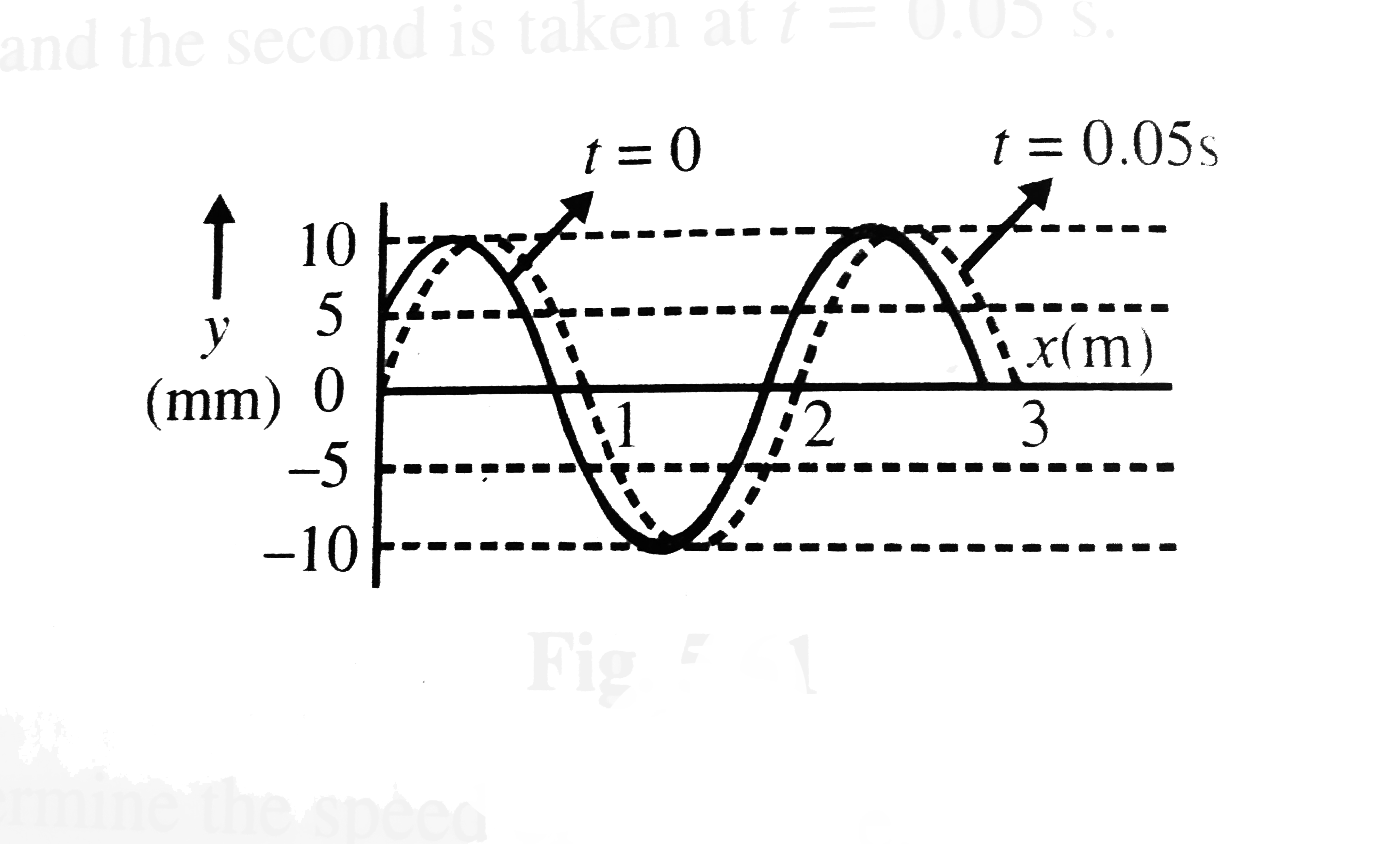
Determine the equation of the wave.
View SolutionA long string having a cross- sectional area `0.80 mm^2` and density `12.5 g cm^(-3)` is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (c ) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (d) What is the velocity of this particle at this instant ?
View SolutionA long string having a cross- sectional area `0.80 mm^2` and density `12.5 g cm^(-3)` is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (c ) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (d) What is the velocity of this particle at this instant ?
View SolutionA long string having a cross- sectional area `0.80 mm^2` and density `12.5 g cm^(-3)` is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (c ) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (d) What is the velocity of this particle at this instant ?
View SolutionA long string having a cross- sectional area `0.80 mm^2` and density `12.5 g cm^(-3)` is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (c ) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (d) What is the velocity of this particle at this instant ?
View SolutionConsider a sinusoidal travelling wave shown in figure. The wave velocity is `+ 40 cm//s`.
Find
(a) the frequency
(b) the phase difference between points `2.5 cm` apart
( c ) how long it takes for the phase at a given position to (pi//3)
(d) the velocity of a particle at `P` at the instant shown.
View SolutionConsider a sinusoidal travelling wave shown in figure. The wave velocity is `+ 40 cm//s`.
Find
(a) the frequency
(b) the phase difference between points `2.5 cm` apart
( c ) how long it takes for the phase at a given position to (pi//3)
(d) the velocity of a particle at `P` at the instant shown.
View SolutionConsider a sinusoidal travelling wave shown in figure. The wave velocity is `+ 40 cm//s`.
Find
(a) the frequency
(b) the phase difference between points `2.5 cm` apart
( c ) how long it takes for the phase at a given position to (pi//3)
(d) the velocity of a particle at `P` at the instant shown.
View SolutionConsider a sinusoidal travelling wave shown in figure. The wave velocity is `+ 40 cm//s`.
Find
(a) the frequency
(b) the phase difference between points `2.5 cm` apart
( c ) how long it takes for the phase at a given position to (pi//3)
(d) the velocity of a particle at `P` at the instant shown.
View SolutionA plane wave propagates along positive x-direction in a homogeneous medium of density `p=200 kg//m^(3)`. Due to propagation of the wave medium particle oscillate. Space density of their oscillation energy is `E=0.16pi^(2) J//m^(3)` and maximum shear strain produced in the mendium is `phi_(0)=8pixx10^(-5)`. if at an instant, phase difference between two particles located at points `(1m,1m,1m)` and `(2m, 2m, 2m,)` is `Deltatheta=144^(@)`, assuming at `t=0` phase of particle at `x=0` to be zero,
Wave velocity is
View SolutionA plane wave propagates along positive x-direction in a homogeneous medium of density `p=200 kg//m^(3)`. Due to propagation of the wave medium particle oscillate. Space density of their oscillation energy is `E=0.16pi^(2) J//m^(3)` and maximum shear strain produced in the mendium is `phi_(0)=8pixx10^(-5)`. if at an instant, phase difference between two particles located at points `(1m,1m,1m)` and `(2m, 2m, 2m,)` is `Deltatheta=144^(@)`, assuming at `t=0` phase of particle at `x=0` to be zero,
wave length is
View SolutionA plane wave propagates along positive x-direction in a homogeneous medium of density `p=200 kg//m^(3)`. Due to propagation of the wave medium particle oscillate. Space density of their oscillation energy is `E=0.16pi^(2) J//m^(3)` and maximum shear strain produced in the mendium is `phi_(0)=8pixx10^(-5)`. if at an instant, phase difference between two particles located at points `(1m,1m,1m)` and `(2m, 2m, 2m,)` is `Deltatheta=144^(@)`, assuming at `t=0` phase of particle at `x=0` to be zero,
Equation of wave is
View SolutionA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at `x=2` cm is found at its mean position and it is moving in positive y-direction at `t=1` s. the amplitude of the wave, the wavelength and the angular frequency of the wave are `0.1m,pi//4m` and `4pi rad//s`, respectively.
The equation of the wave is
View SolutionA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at `x=2` cm is found at its mean position and it is moving in positive y-direction at `t=1` s. the amplitude of the wave, the wavelength and the angular frequency of the wave are `0.1m,pi//4m` and `4pi rad//s`, respectively.
The speed of particle at `x=2 m` and `t=1 s` is
View SolutionA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at `x=2` cm is found at its mean position and it is moving in positive y-direction at `t=1` s. the amplitude of the wave, the wavelength and the angular frequency of the wave are `0.1m,pi//4m` and `4pi rad//s`, respectively.
The instantaneous power transfer through `x=2 m` and `t=1.125 s` is
View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are `mu,4mu,9mu and 16mu`, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency `f` (ignore any reflection and absorption). string has been stretched under a tension `F`.

Find the time taken by wave to reach from source end to fixed end.
View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are `mu,4mu,9mu and 16mu`, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency `f` (ignore any reflection and absorption). string has been stretched under a tension `F`.

Find the ratio of wavelength of the wave on four string, starting from right hand side.
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in `0.4 s` and in each up and down movement the hand moves by a height of `0.3 m`. The wavelength of the waves on the string is `0.8 m`.
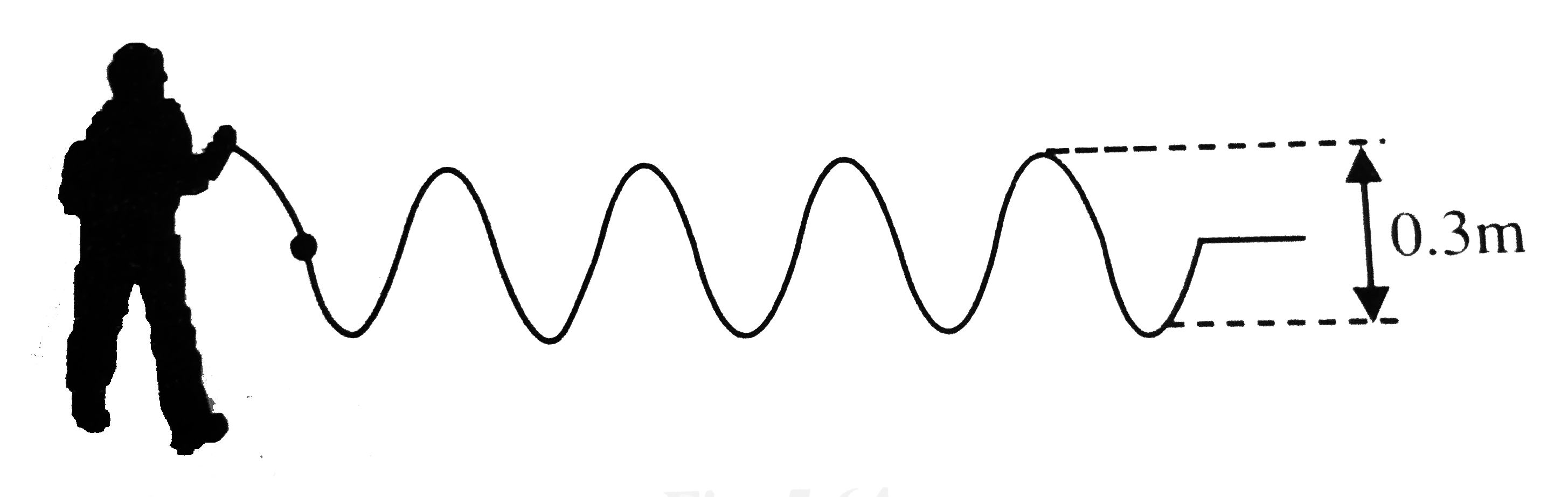
The frequency of the wave is
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in `0.4 s` and in each up and down movement the hand moves by a height of `0.3 m`. The wavelength of the waves on the string is `0.8 m`.
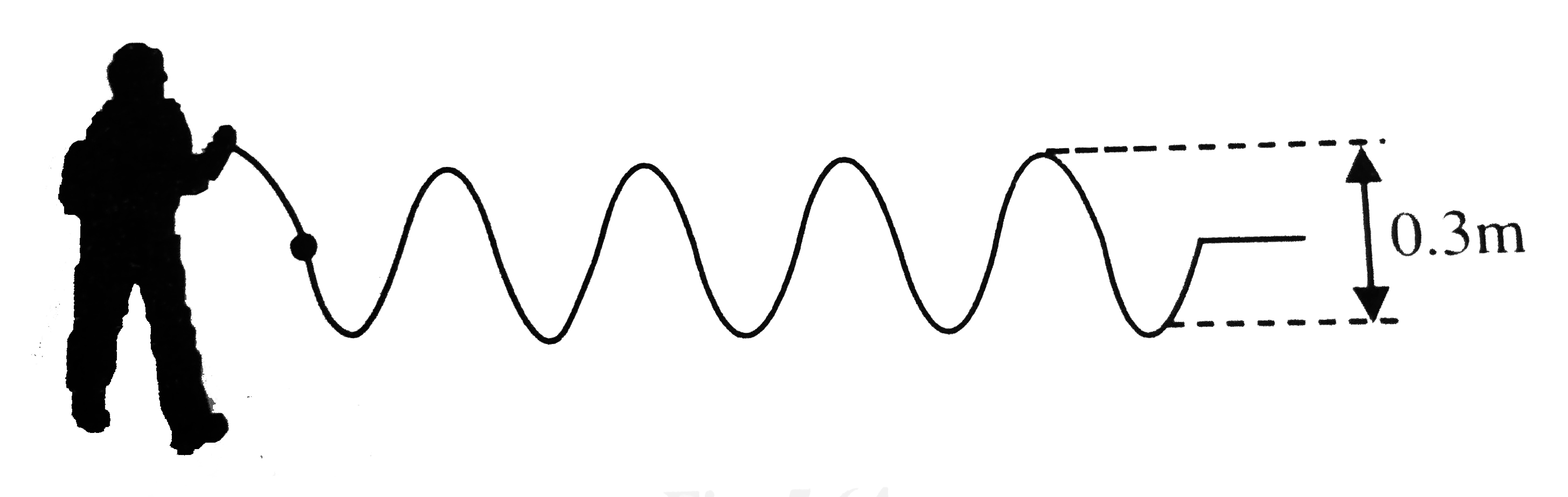
The amplitude of the wave is
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in `0.4 s` and in each up and down movement the hand moves by a height of `0.3 m`. The wavelength of the waves on the string is `0.8 m`.

The wave speed is
View SolutionA child playing with a long rope ties one end holds the other. The rope is stretched taut along the horizontal. The child shakes the end he is holding, up and down, in a sinusoidal manner with amplitude `10 cm` and frequency `3` Hz.
Speed of the wave is `15 m//s` and, at `t=0`, displacement at the child's end is maximum positive. Assuming that there is no wave reflected from the fixed end, so that the waves in the rope are plane progressive waves, answer the following quetions.
(Also assume that the wave propagates along the positive `x-`direction.)
A wave function that describe the wave in the given sutuation is
View SolutionA child playing with a long rope ties one end holds the other. The rope is stretched taut along the horizontal. The child shakes the end he is holding, up and down, in a sinusoidal manner with amplitude `10 cm` and frequency `3` Hz.
Speed of the wave is `15 m//s` and, at `t=0`, displacement at the child's end is maximum positive. Assuming that there is no wave reflected from the fixed end, so that the waves in the rope are plane progressive waves, answer the following quetions.
(Also assume that the wave propagates along the positive `x-`direction.)
A wave function that describe the wave in the given sutuation is
View SolutionA child playing with a long rope ties one end holds the other. The rope is stretched taut along the horizontal. The child shakes the end he is holding, up and down, in a sinusoidal manner with amplitude `10 cm` and frequency `3` Hz.
Speed of the wave is `15 m//s` and, at `t=0`, displacement at the child's end is maximum positive. Assuming that there is no wave reflected from the fixed end, so that the waves in the rope are plane progressive waves, answer the following quetions.
(Also assume that the wave propagates along the positive x-direction.)
Phase difference between the child,s end and a point `2.5m` from the child's end will be
View SolutionOne end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension `8 N` . Let us consider the length of the rope to be along x-axis. A simple harmonic oscillator at `x=0` generates a transverse wave of frequency `100 Hz` and amplitude `2 cm` along the rope. Mass of a unit length of the rope is `20 g//m`. ignoring the effect of gravity, answer the following questions.
Wavelength of the wave is
View SolutionOne end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension `8 N` . Let us consider the length of the rope to be along x-axis. A simple harmonic oscillator at `x=0` generates a transverse wave of frequency `100 Hz` and amplitude `2 cm` along the rope. Mass of a unit length of the rope is `20 g//m`. ignoring the effect of gravity, answer the following questions.
Assuming that the oscillator has its maximum negative displacement at `t=0`, wave equation function ) for the wave can be expressed as `y=`
View SolutionOne end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension `8 N` . Let us consider the length of the rope to be along x-axis. A simple harmonic oscillator at `x=0` generates a transverse wave of frequency `100 Hz` and amplitude `2 cm` along the rope. Mass of a unit length of the rope is `20 g//m`. ignoring the effect of gravity, answer the following questions.
which of the following is correct?
View SolutionOne end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension `8 N` . Let us consider the length of the rope to be along x-axis. A simple harmonic oscillator at `x=0` generates a transverse wave of frequency `100 Hz` and amplitude `2 cm` along the rope. Mass of a unit length of the rope is `20 g//m`. ignoring the effect of gravity, answer the following questions.
maximum magnitude of transverse acceleration of any point on the rope will be nearly
View SolutionOne end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension `8 N` . Let us consider the length of the rope to be along x-axis. A simple harmonic oscillator at `x=0` generates a transverse wave of frequency `100 Hz` and amplitude `2 cm` along the rope. Mass of a unit length of the rope is `20 g//m`. ignoring the effect of gravity, answer the following questions.
Tension in the given rope remaining the same, if a simple harmonic oscillator of frequency `200 Hz` is used instead of the earlier oscillator of frequency `100 Hz`
View SolutionA rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension `T` . Suppose at `t=0`, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant `t`.
Ignoring the effect of gravity, answer the following quetions.
A.. If you move your hand up and down once but to a greater distance and in the same amount of time.
View SolutionA rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension `T` . Suppose at `t=0`, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant `t`.
Ignoring the effect of gravity, answer the following quetions.
If you move your hand up and down once but to a greater distance and in the same amount of time.
View SolutionA rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension `T` . Suppose at `t=0`, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant `t`.
Ignoring the effect of gravity, answer the following quetions.
If you use a string of same length but of greater mass
View SolutionA rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension `T` . Suppose at `t=0`, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant `t`.
Ignoring the effect of gravity, answer the following quetions.
In all the above, quetions we have considered a fixed value of tension. however, if tension in a given rope is increased and a pulse is genrated as described,
View SolutionA simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for `x=0`(curve 1) and `x=7` (curve 2)
The two particle are with a span of onewavelength.
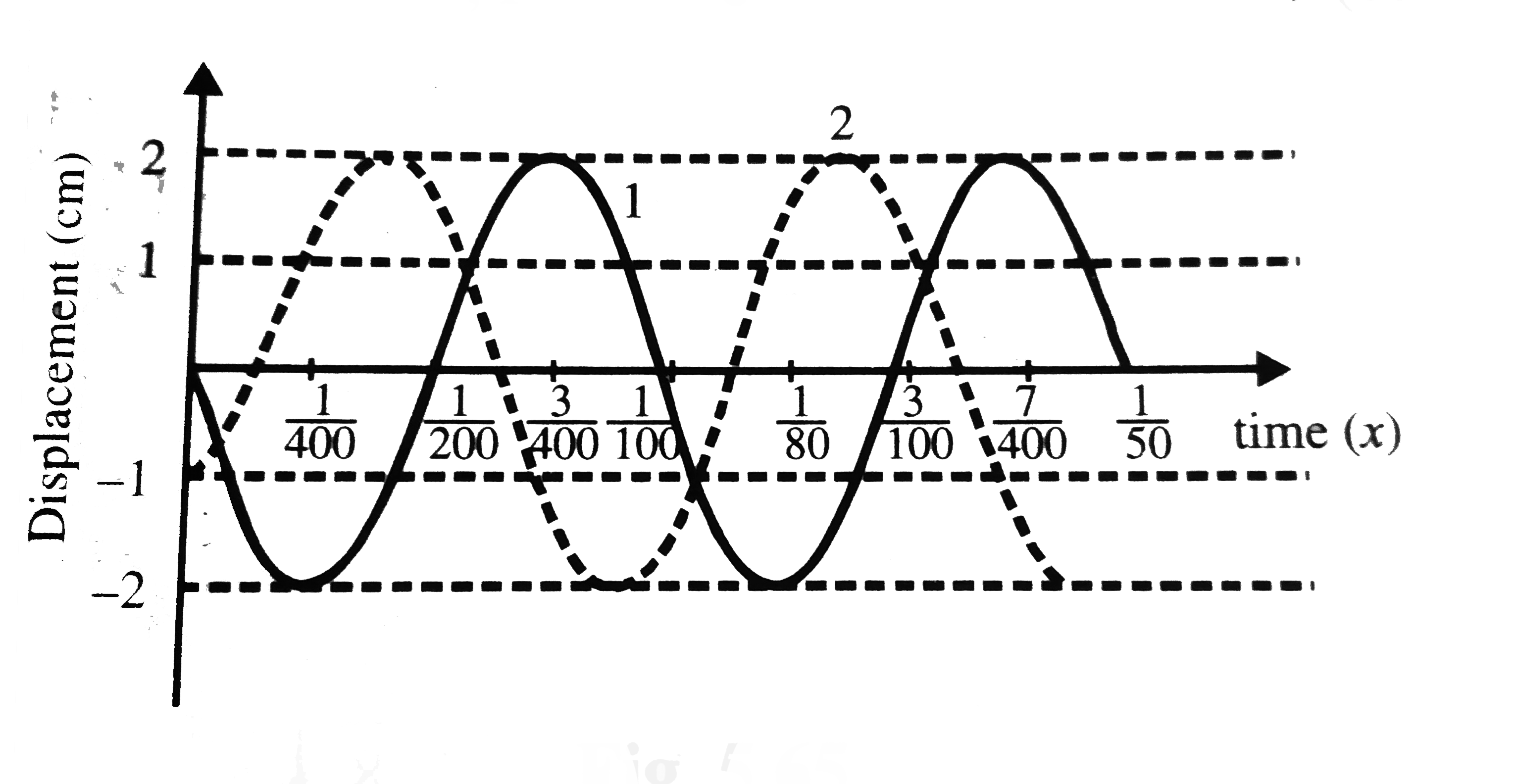
The wavelength of the wave is
View SolutionA simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for `x=0`(curve 1) and `x=7` (curve 2)
The two particle are with a span of onewavelength.
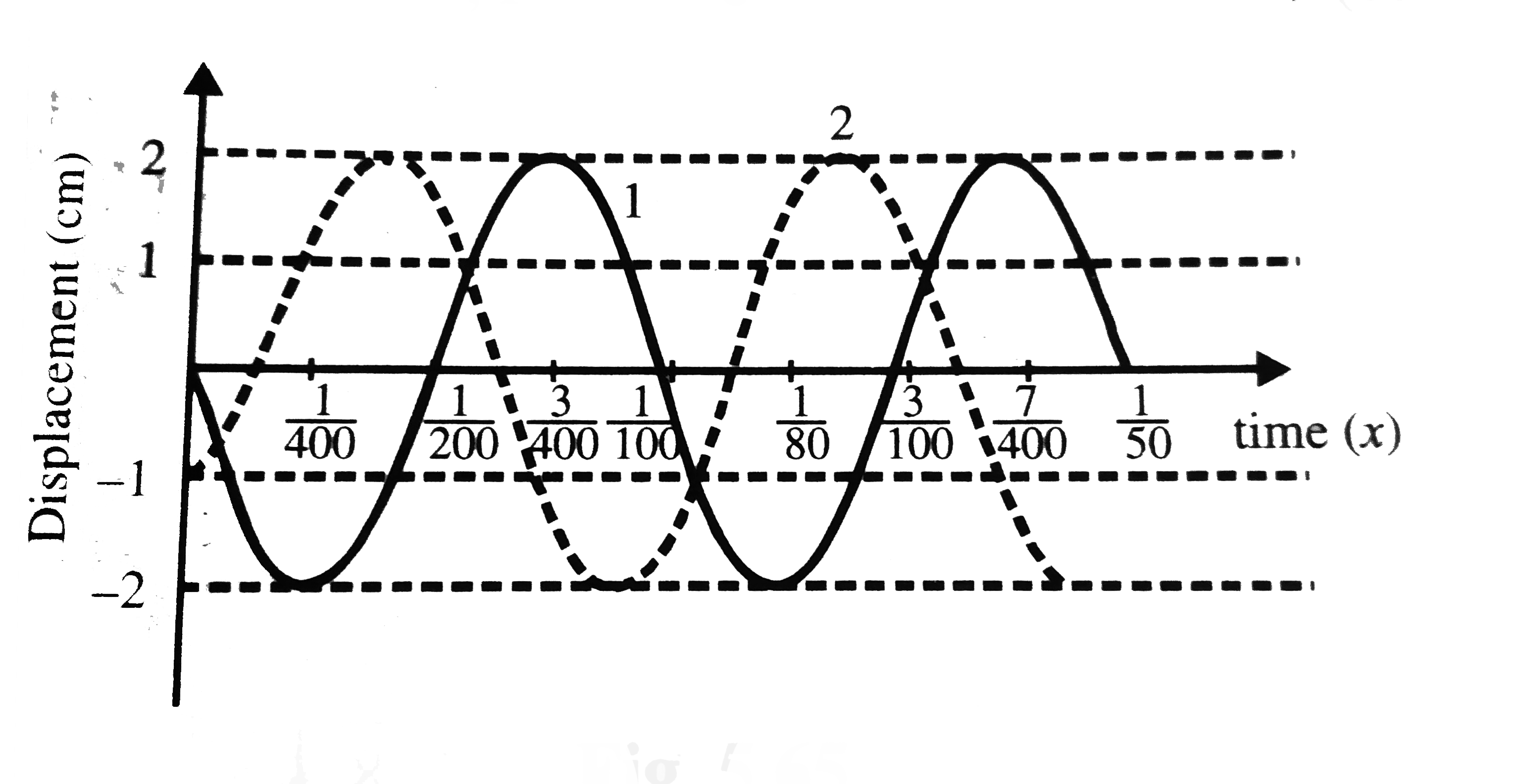
The speed of the wave is
View SolutionFigure. shows two snapshots of medium particle supporting a plane progressive wave travelling along positive `x-`axos, corresponding to instants `t=0.002 s` and `t=0.008 s`, respectively shown by curves numbered `1` and `2`.
Assume that the interval between the two snapshots is less than the time period.

Velocity of the wave is
View SolutionFigure .shows two snapshots of medium particle supporting a plane progressive wave travelling along positive x-axos, corresponding to instants `t=0.002 s` and `t=0.008 s`, respectively shown by curves numbered `1` and `2`.
Assume that the interval between the two snapshots is less than the time period.
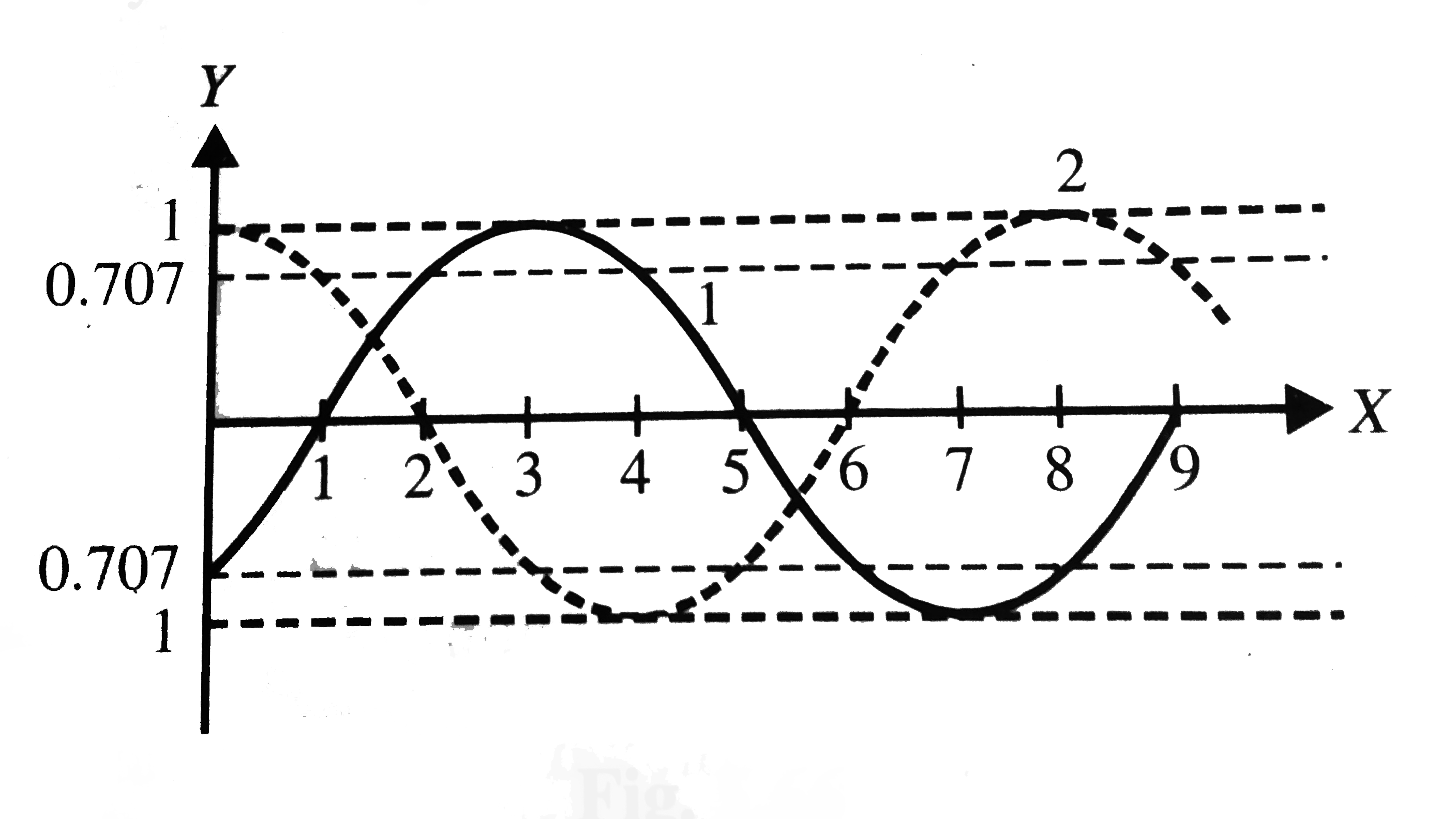
The frequency of the wave
View SolutionThe figure shows a snap photograph of a vibrating string at `t = 0`. The particle `P` is observed moving up with velocity `20sqrt(3) cm//s`. The tangent at `P` makes an angle `60^(@)` with x-axis.
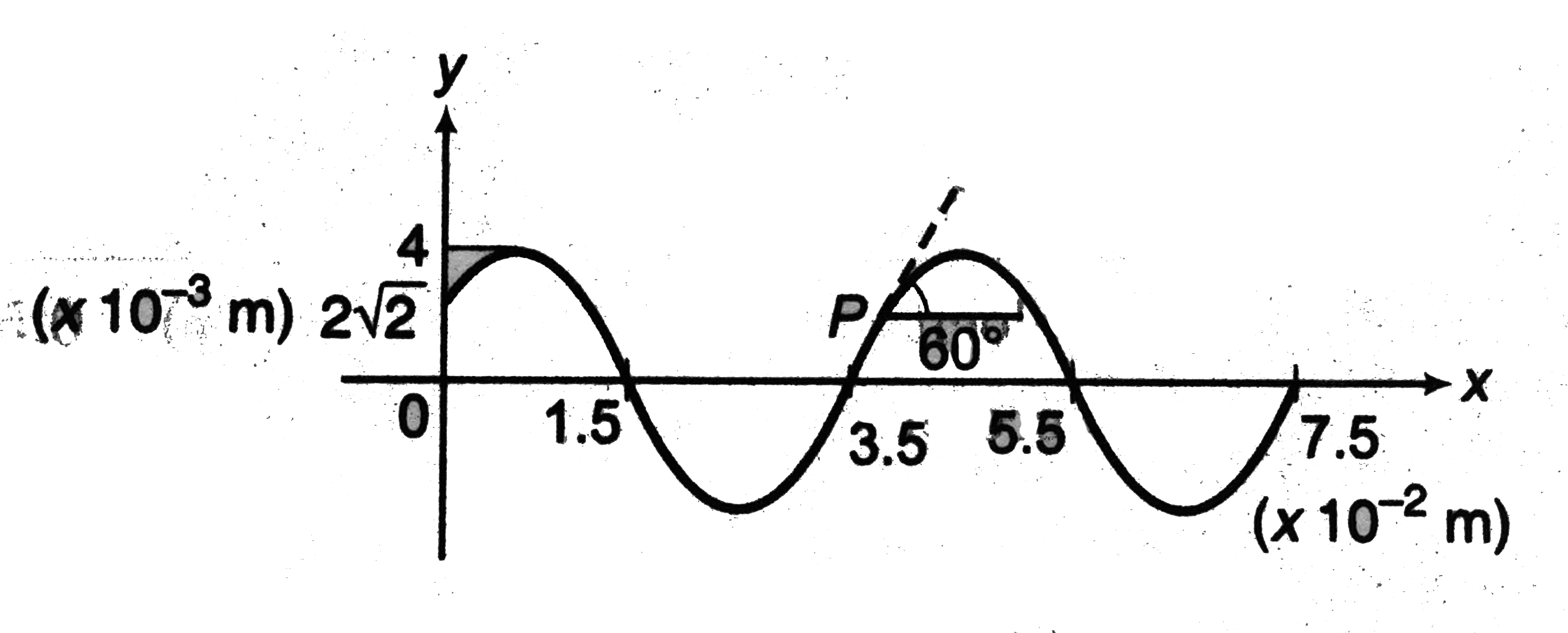
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is `50g//m`.
View SolutionThe figure shows a snap photograph of a vibrating string at `t = 0`. The particle `P` is observed moving up with velocity `20sqrt(3) cm//s`. The tangent at `P` makes an angle `60^(@)` with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is `50g//m`.
View SolutionA pulse is started at a time `t=0` along the `+x`direction on a long, taut string. The shape of the pulse at `t=0` is given by function `f(x)` with
here `f` and `x` are in centimeters. The linear mass density of the string is `50 g//m` and it is under a tension of `5N`.
There shape of the string is drawn at `t=0` and the area of the pulse enclosed by the string the x-axis is measured. it will be equjal to
View SolutionA pulse is started at a time `t=0` along the `+x`direction on a long, taut string. The shape of the pulse at `t=0` is given by function `f(x)` with ` {((x-vt)/4+1,for,vt-4ltx,le,vt),(-(x-vt)+1,for,vt,ltxlt,vt+1):}`
`0`, otherwise
`{((x-vt)/4+1,for,vt-4ltx,le,vt),(-(x-vt)+1,for,vt,ltxlt,vt+1):}`
`0`, otherwise
here `f` and `x` are in centimeters. The linear mass density of the string is `50 g//m` and it is under a tension of `5N`.
The verticle displacement of the particle of the string at `x=7 cm` and `t=0.01 s` will be
View SolutionA pulse is started at a time `t=0` along the `+x`direction on a long, taut string. The shape of the pulse at `t=0` is given by function `f(x)` with
here `f` and `x` are in centimeters. The linear mass density of the string is `50 g//m` and it is under a tension of `5N`.
The transverse velocity of the particle at `x=13 cm` and `t=0.015 s` will be
View Solution
Comprehension questions and complete solutions for chapter TRAVELLING WAVES of CENGAGE PHYSICS (HINGLISH) of Class 11