Complete Solutions to Comprehension of chapter KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS |
| CENGAGE PHYSICS | Comprehension |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
A fixed mass of gas is taken through a process `A rarr B rarr C rarrA`. Here `A rarr B` is isobaric, `B rarr C` is adiabatic and `C rarr A `is isothermal.
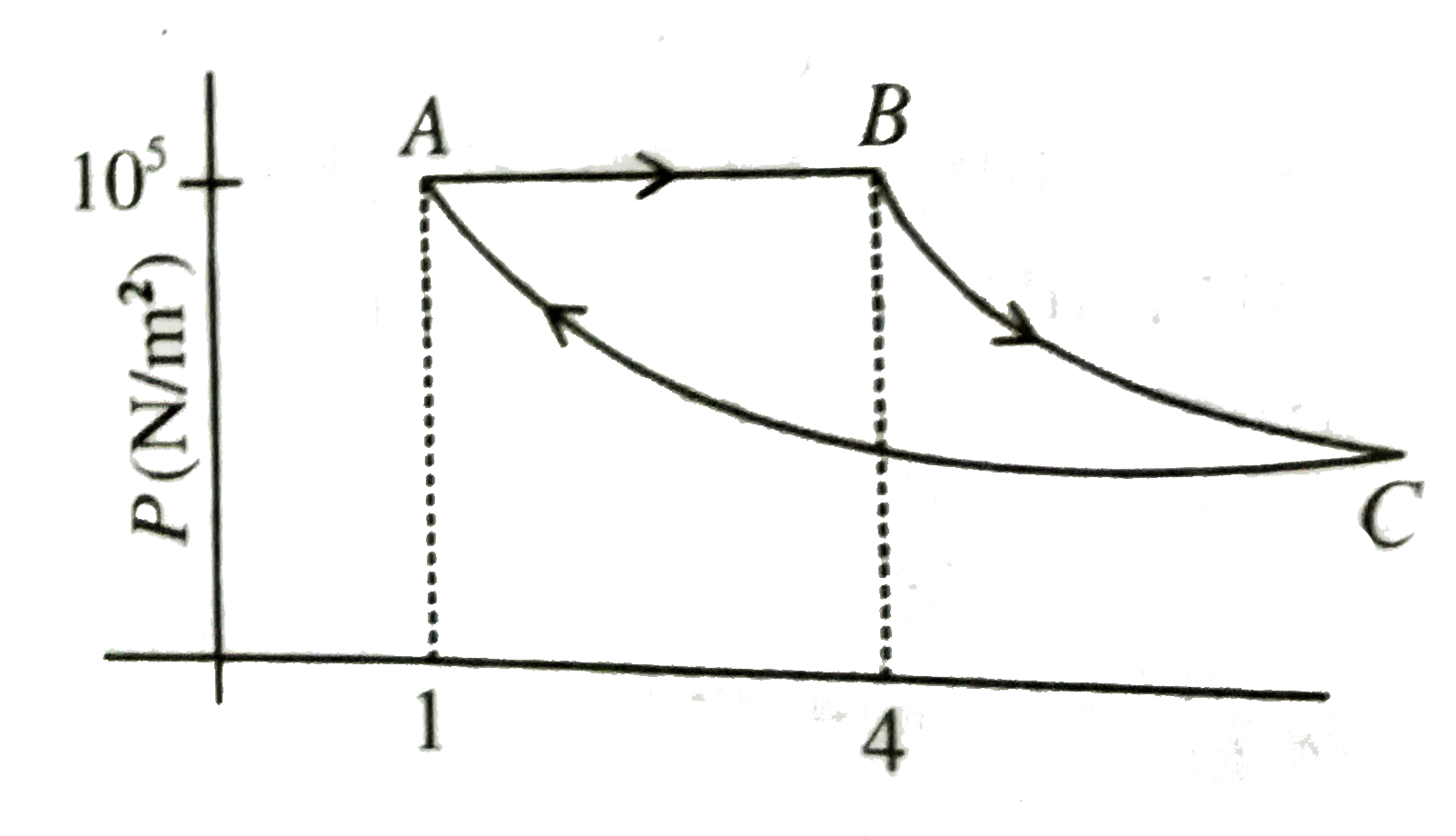
Find pressure at `C`.
View SolutionA fixed mass of gas is taken through a process `A rarr B rarr C rarrA`. Here `A rarr B` is isobaric, `B rarr C` is adiabatic and `C rarr A `is isothermal.
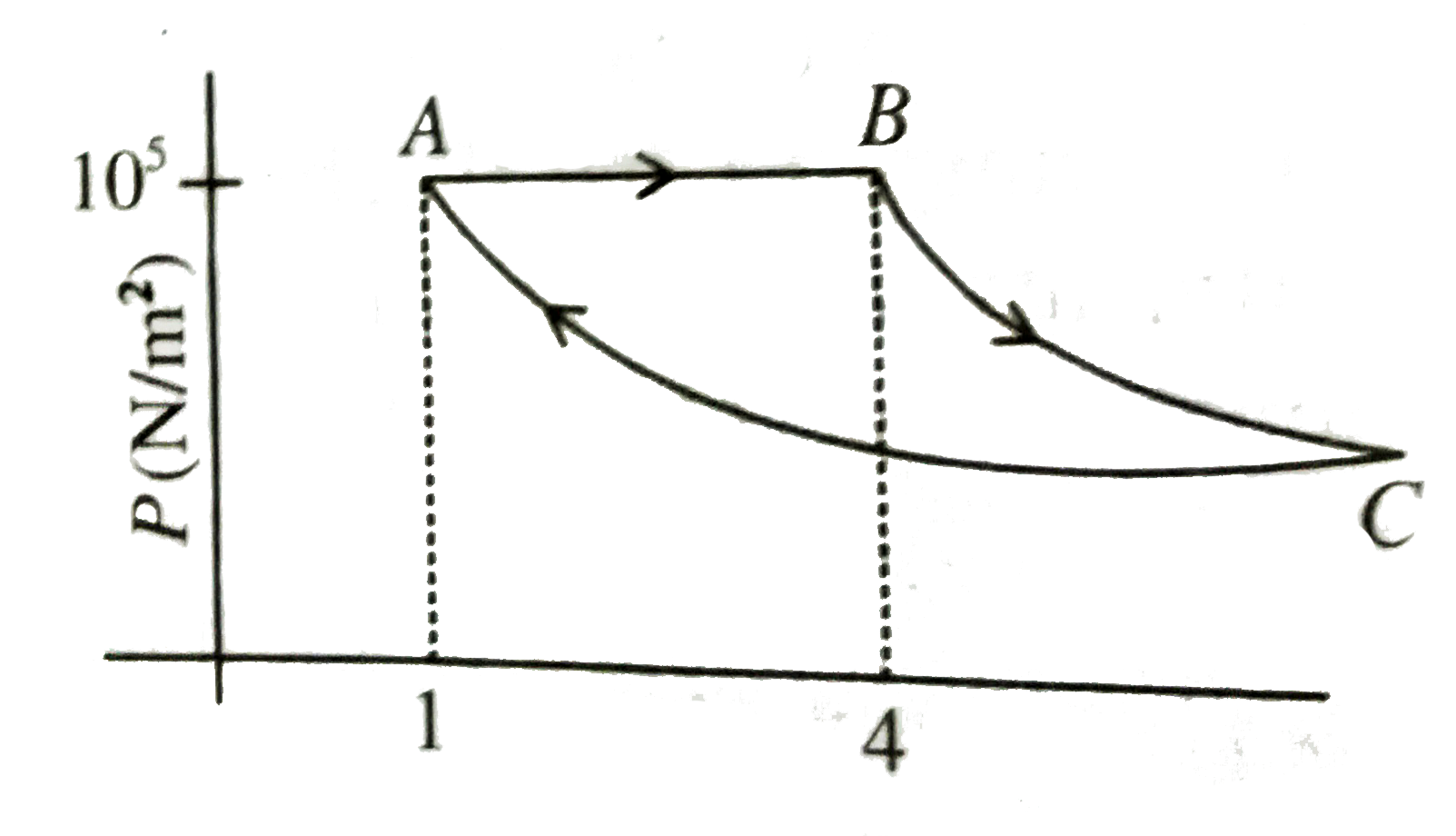 Find volume at `C`.
Find volume at `C`.
View SolutionA fixed mass of gas is taken through a process `A rarr B rarr C rarrA`. Here `A rarr B` is isobaric, `B rarr C` is adiabatic and `C rarr A `is isothermal.
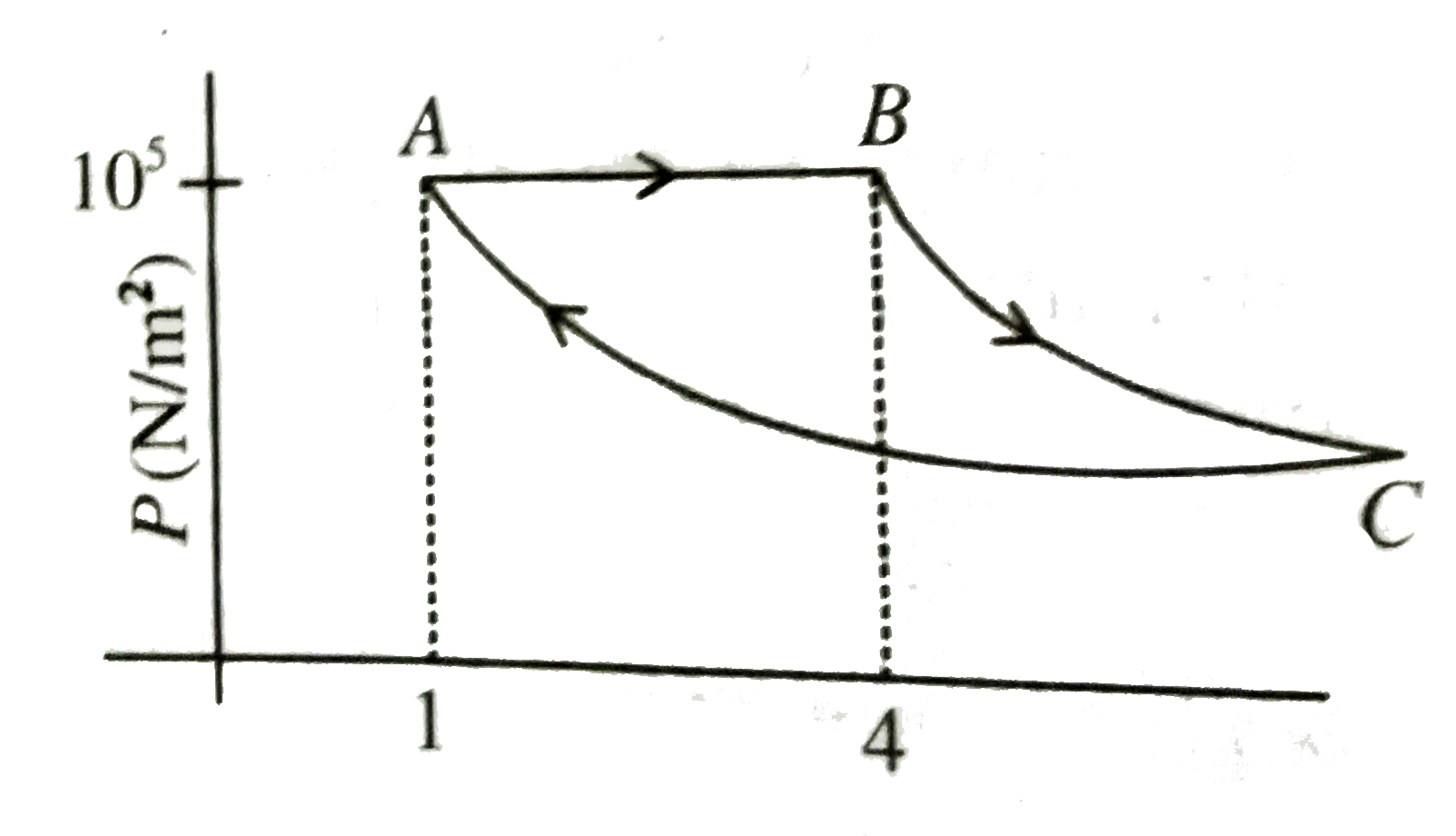
Find work done is the process `(` take `gamma=1.5)`.
View SolutionFour moles of an ideal gas is initially in state `A` having pressure ` 2 xx 10^(5) N//m^(2)` and temperature ` 200 K` . Keeping the pressure constant the gas is taken to state `B` at temperature of `400K`. The gas is then taken to a state `C` in such a way that its temperature increases and volume decreases. Also from `B` to `C` , the magnitude of `dT//dV` increases. The volume of gas at state `C` is eqaul to its volume at statem `A`. Now gas is taken to initial state `A` keeping volume constant. A total `1000 J` of heat is withdrawn from the sample of the cyclic process . Take `R=8.3 J// K// mol`.
Which graph between temperature `T` and volume `V` for the cyclic process is correct.
View SolutionFour moles of an ideal gas is initially in state `A` having pressure ` 2 xx 10^(5) N//m^(2)` and temperature ` 200 K` . Keeping the pressure constant the gas is taken to state `B` at temperature of `400K`. The gas is then taken to a state `C` in such a way that its temperature increases and volume decreases. Also from `B` to `C` , the magnitude of `dT//dV` increases. The volume of gas at state `C` is eqaul to its volume at statem `A`. Now gas is taken to initial state `A` keeping volume constant. A total `1000 J` of heat is withdrawn from the sample of the cyclic process . Take `R=8.3 J// K// mol`.
The work done in path `B` to `C` is
View SolutionFour moles of an ideal gas is initially in state `A` having pressure ` 2 xx 10^(5) N//m^(2)` and temperature ` 200 K` . Keeping the pressure constant the gas is taken to state `B` at temperature of `400K`. The gas is then taken to a state `C` in such a way that its temperature increases and volume decreases. Also from `B` to `C` , the magnitude of `dT//dV` increases. The volume of gas at state `C` is eqaul to its volume at statem `A`. Now gas is taken to initial state `A` keeping volume constant. A total `1000 J` of heat is withdrawn from the sample of the cyclic process . Take `R=8.3 J// K// mol`. The volume of gas at state `C` is
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by `W` and increase in internal energy as `Delta U` then
`W prop Delta U`
or `W=K_(1) DeltaU` ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
`PV^( eta)= K_(2)` (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat `'C'` for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat `'C'` with `eta` for a monatomic gas is plotted as in the graph shown.

In the graph shown, the `y-` coordinate of point `A` is ( for monatomic gas )
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by `W` and increase in internal energy as `Delta U` then
`W prop Delta U`
or `W=K_(1) DeltaU` ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
`PV^( eta)= K_(2)` (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat `'C'` for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat `'C'` with `eta` for a monatomic gas is plotted as in the graph shown.

In the graph shown, the `y-` coordinate of point `A` is ( for monatomic gas )
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by `W` and increase in internal energy as `Delta U` then
`W prop Delta U`
or `W=K_(1) DeltaU` ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
`PV^( eta)= K_(2)` (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat `'C'` for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat `'C'` with `eta` for a monatomic gas is plotted as in the graph shown.

In the graph shown, the `y-` coordinate of point `A` is ( for monatomic gas )
View SolutionFigure, shows the variation of potential energy `(U)` of 2 mol of Argon gas with its density in a cyclic process `ABCA`. The gas was initiallly in the state `A` whose pressure and temperature are `P_(A)=2 atm, T_(A)=300K`, respectively. It is also stated the path `AB` is a rectangular hyperbola and the internal energy of the gas at state `C` is `3000r`. Based on the above information answer the following question `:`
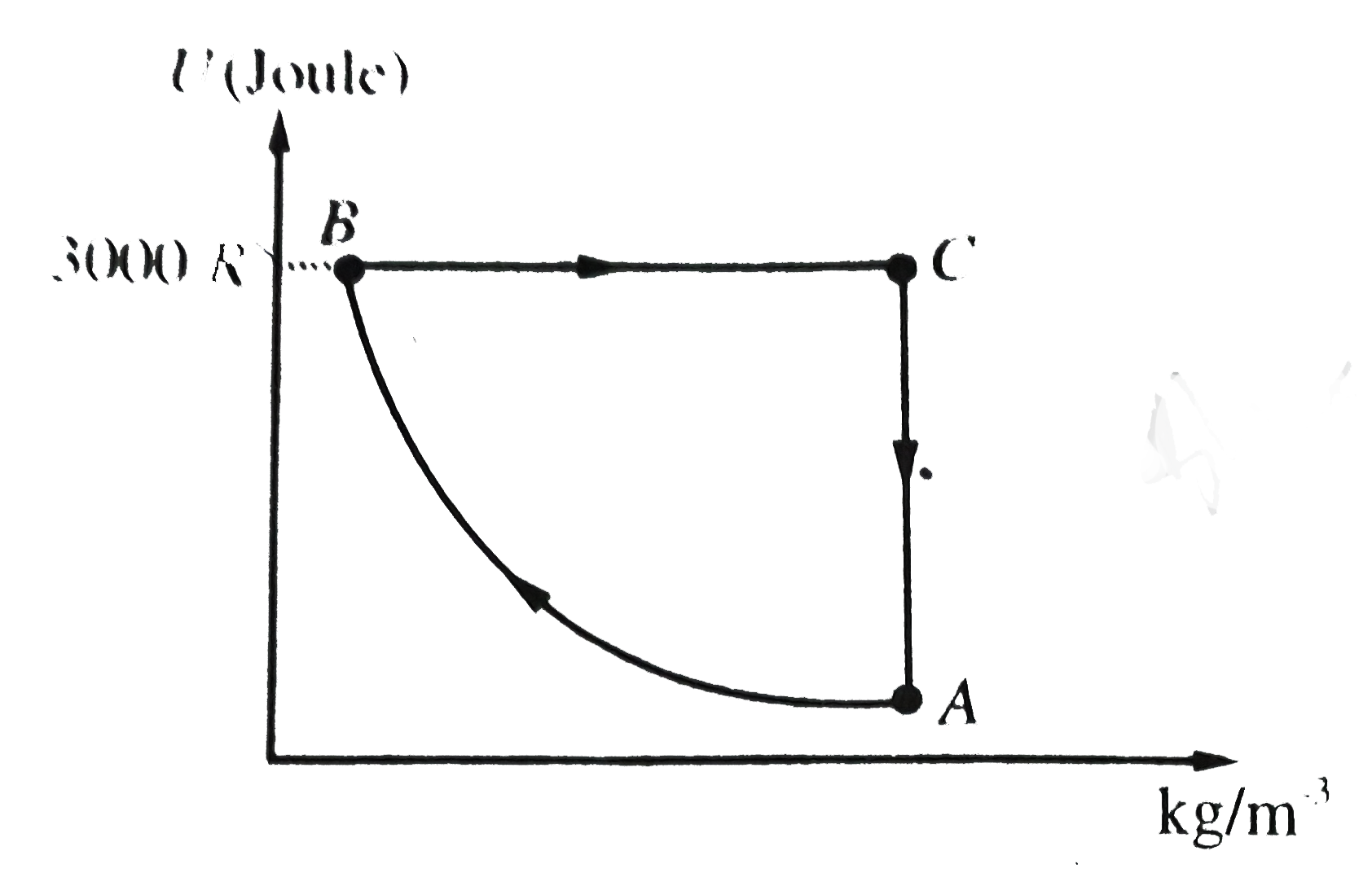
View SolutionFigure, shows the variation of potential energy `(U)` of 2 mol of Argon gas with its density in a cyclic process `ABCA`. The gas was initiallly in the state `A` whose pressure and temperature are `P_(A)=2 atm, T_(A)=300K`, respectively. It is also stated the path `AB` is a rectangular hyperbola and the internal energy of the gas at state `C` is `3000r`. Based on the above information answer the following question `:`
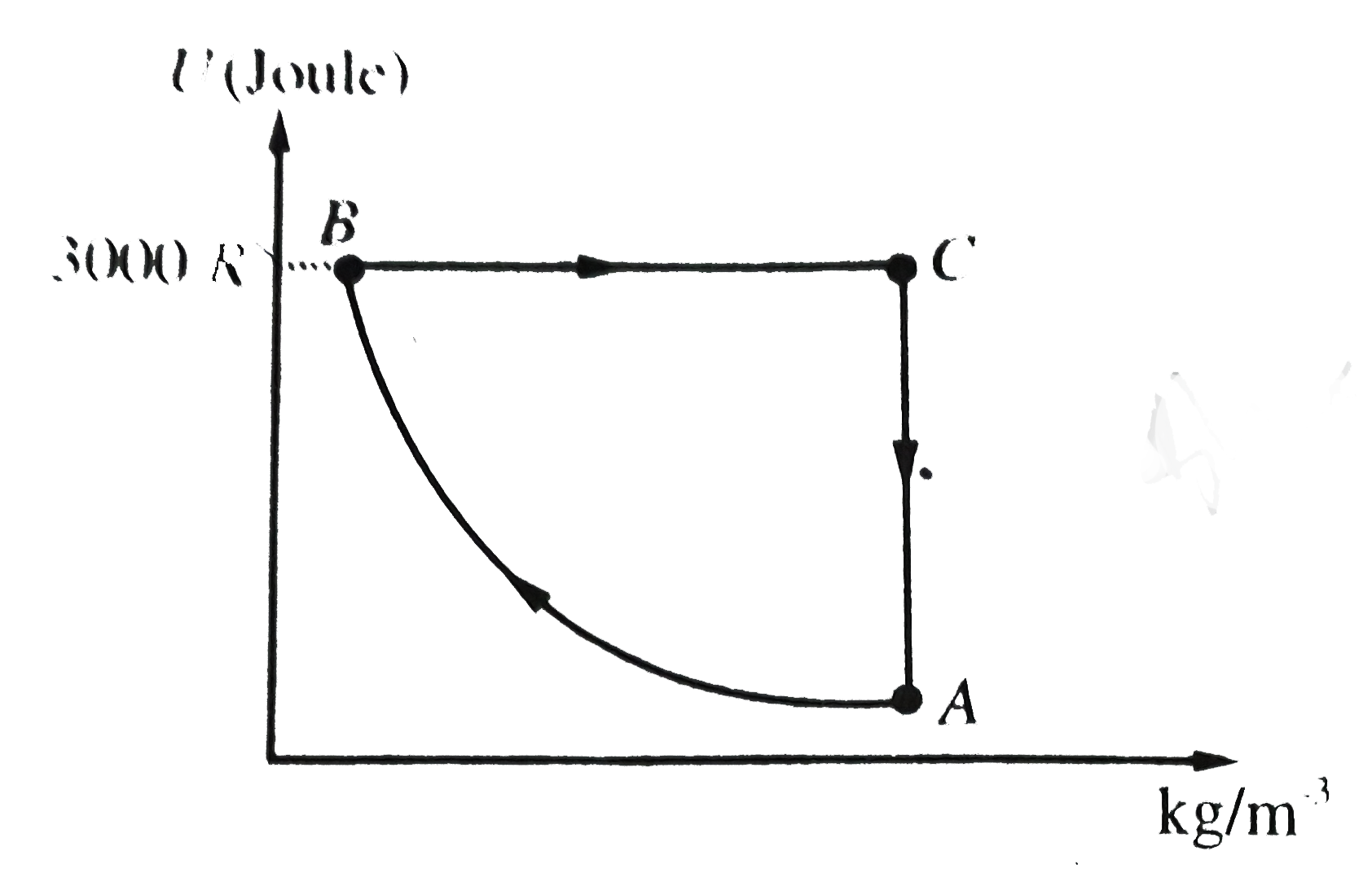
The heat supplied to the gas in the process `AB` is
View SolutionFigure, shows the variation of potential energy `(U)` of 2 mol of Argon gas with its density in a cyclic process `ABCA`. The gas was initiallly in the state `A` whose pressure and temperature are `P_(A)=2 atm, T_(A)=300K`, respectively. It is also stated the path `AB` is a rectangular hyperbola and the internal energy of the gas at state `C` is `3000r`. Based on the above information answer the following question `:`
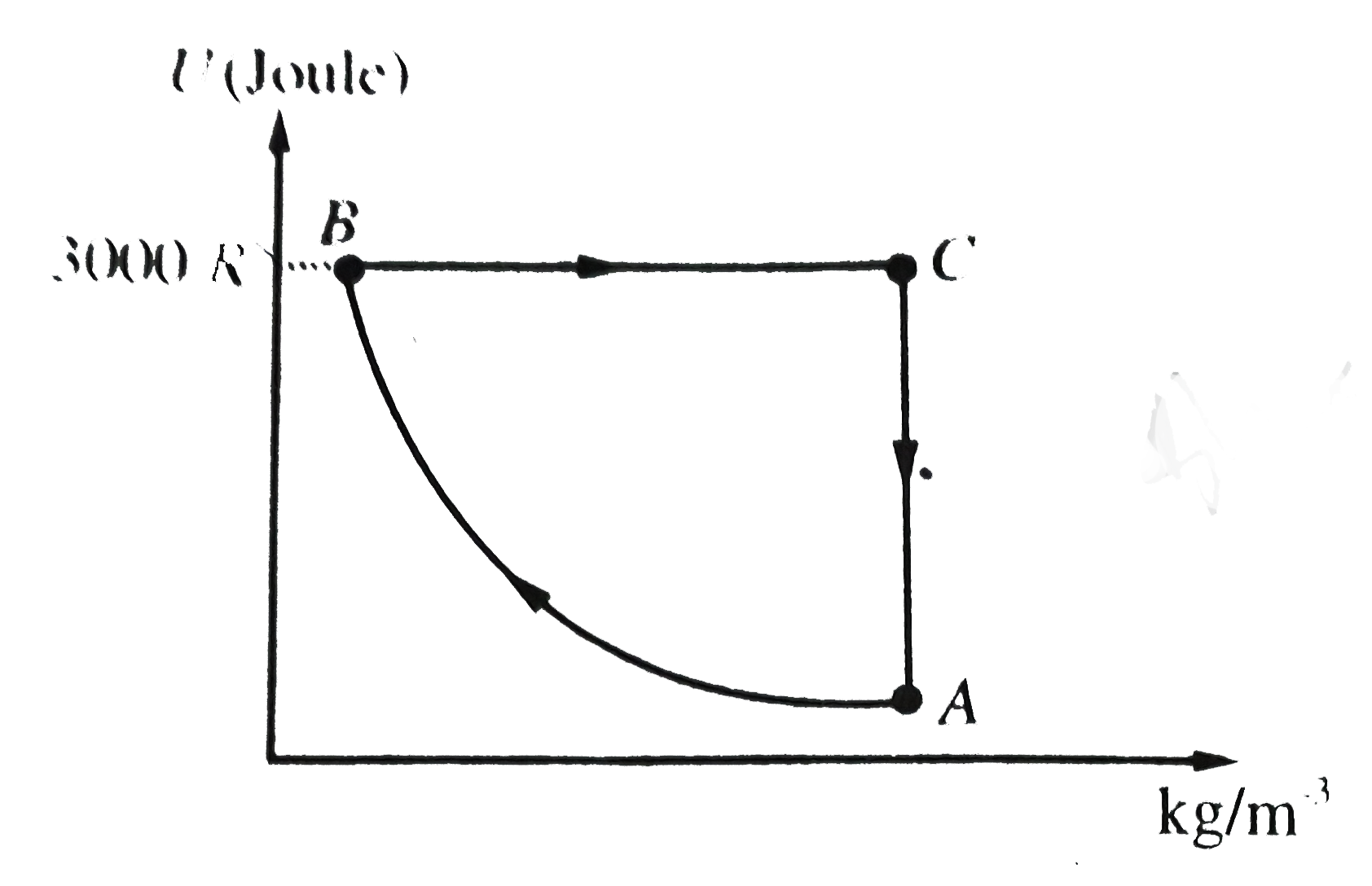
Heat supplied in the process `CA` is
View SolutionOne mole of an ideal gas has an interal energy given by `U=U_(0)+2PV` , where `P` is the pressure and `V` the volume of the gas. `U_(0)` is a constant. This gas undergoes the quasi`-` static cyclic process `ABCD` as shown in the `U-V` diagram.
 The molar heat capacity of the gas at constant pressure is
The molar heat capacity of the gas at constant pressure is
View SolutionOne mole of an ideal gas has an interal energy given by `U=U_(0)+2PV` , where `P` is the pressure and `V` the volume of the gas. `U_(0)` is a constant. This gas undergoes the quasi`-` static cyclic process `ABCD` as shown in the `U-V` diagram.

The work done by the ideal gas in the process `AB` is
View SolutionOne mole of an ideal gas has an interal energy given by `U=U_(0)+2PV` , where `P` is the pressure and `V` the volume of the gas. `U_(0)` is a constant. This gas undergoes the quasi`-` static cyclic process `ABCD` as shown in the `U-V` diagram.

The gas must be
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy.
The molar specific heat of the gas in this process is given by `C` whose value is
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy.
The process can be represented by the equation `TV^(n) =` constant, where the value of `n` is
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy.
If in the above process, the initial temperature of the gas be `T_(0)` and the final volume by 32 times the initial volume, the work done `(` in joules `)` by the gas during the process will be
View SolutionA cylinder containing an ideal gas ( see figure ) and closed by a movable pistong is submerged in an ice- water mixture. The pistone is quickly pushed down from position (1) to position (2)( process `AB)`. The piston is held at position `(2)` until the gas is again at `0^(@)C` ( processs `BC)`. Then the pistone is slowly raised back to position (1) ( process `CA)`
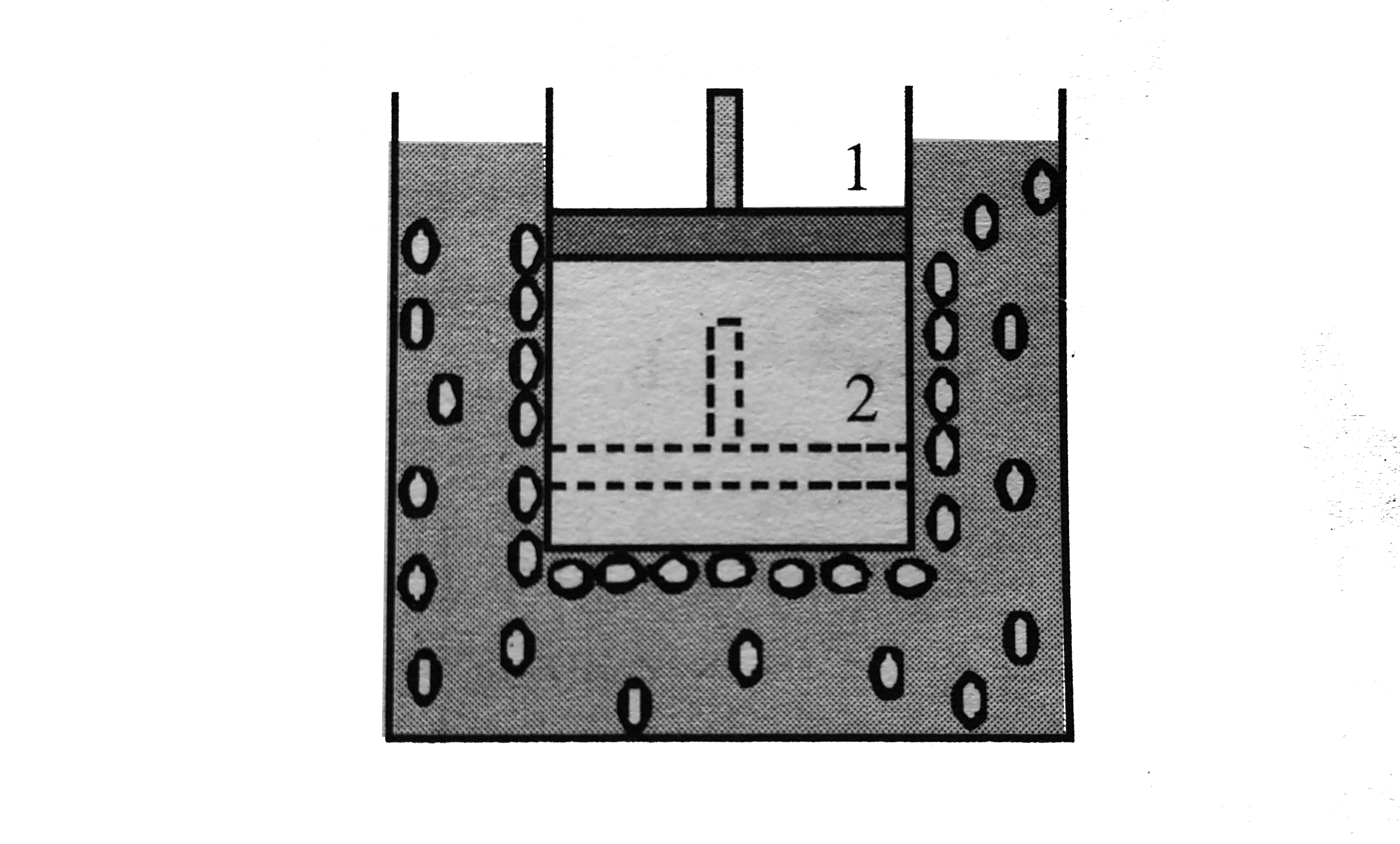
Which of the following `P-V` diagram will correctly represent the processes `AB, BC` and `CA` and the cycle `ABCA?`
View SolutionA cylinder containing an ideal gas ( see figure ) and closed by a movable pistong is submerged in an ice- water mixture. The pistone is quickly pushed down from position (1) to position (2)( process `AB)`. The piston is held at position `(2)` until the gas is again at `0^(@)C` ( processs `BC)`. Then the pistone is slowly raised back to position (1) ( process `CA)`

Which of the following `P-V` diagram will correctly represent the processes `AB, BC` and `CA` and the cycle `ABCA?`
View SolutionA cylinder containing an ideal gas ( see figure ) and closed by a movable pistong is submerged in an ice- water mixture. The pistone is quickly pushed down from position (1) to position (2)( process `AB)`. The piston is held at position `(2)` until the gas is again at `0^(@)C` ( processs `BC)`. Then the pistone is slowly raised back to position (1) ( process `CA)`
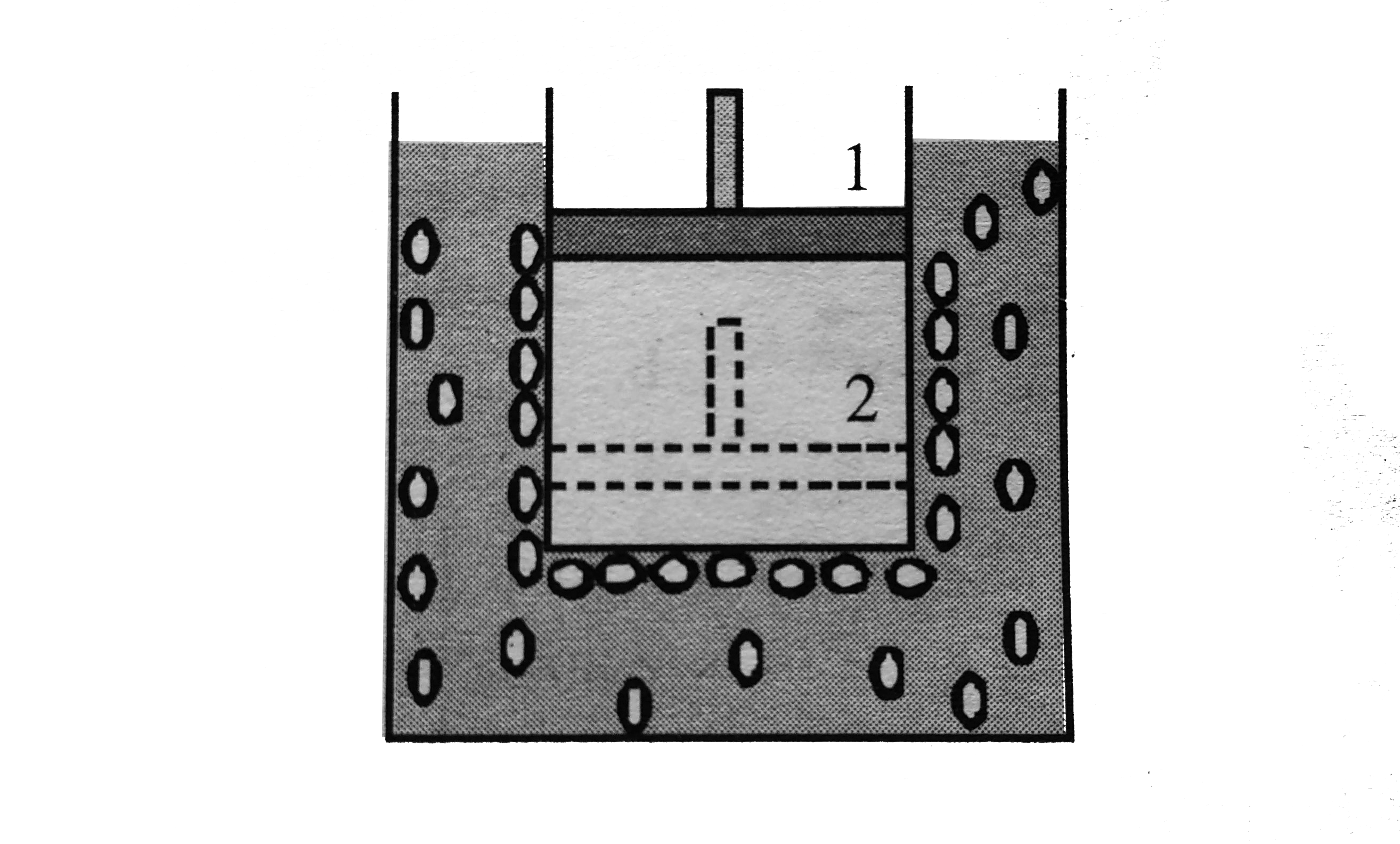
Which of the following `P-V` diagram will correctly represent the processes `AB, BC` and `CA` and the cycle `ABCA?`
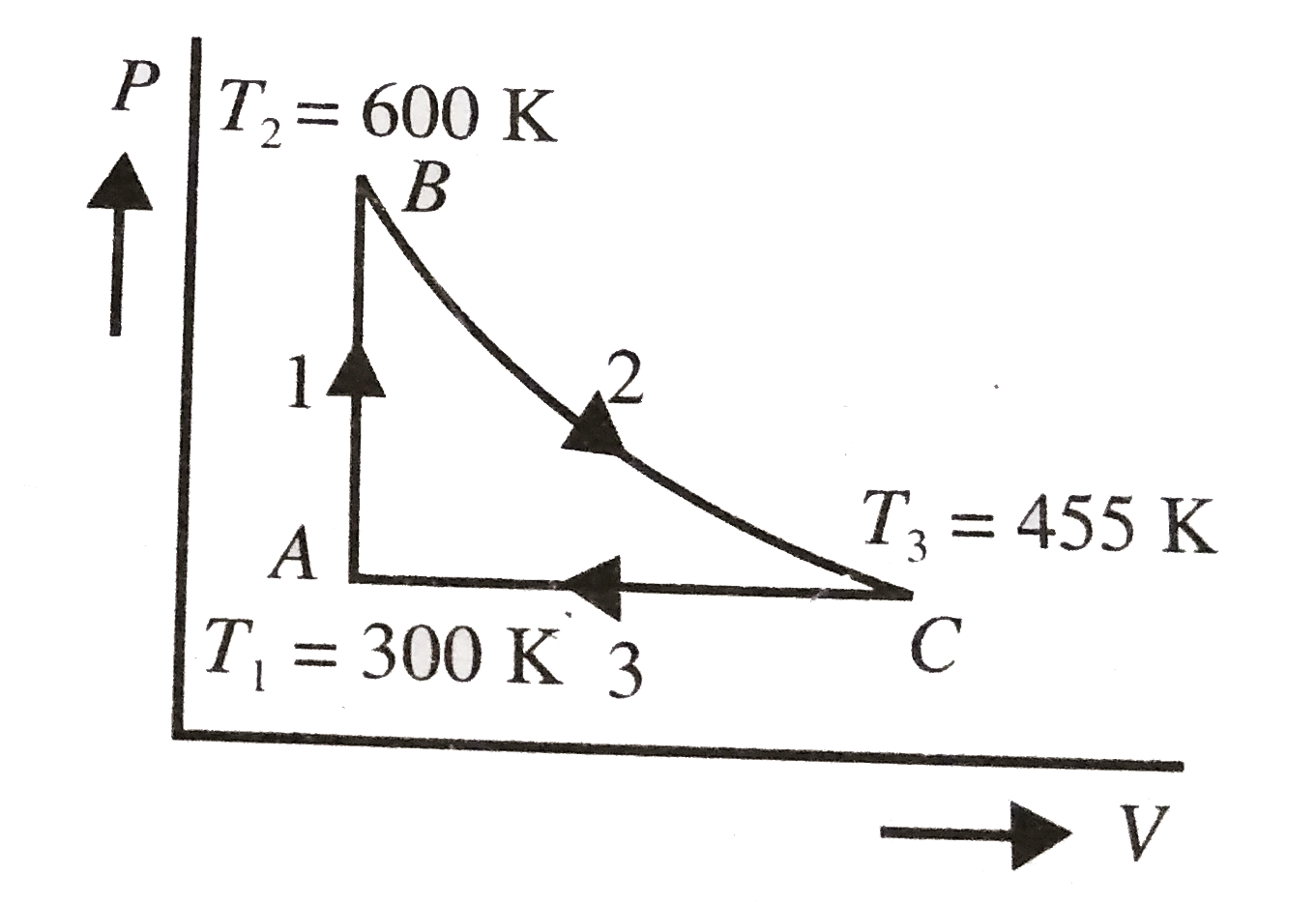
View SolutionA reversible heat engine carries `1 mol` of an ideal monatomic gas around the cycle `ABCA`, as shown in the diagram. The process `BC` is adiabatic. Call the processes `AB, BC` and `CA` as `1,2` and `3` and the heat `( DeltaQ)_(r)`, change in internal energy `(DeltaU)`, and work done `( DeltaW)_(r), r=1,2,3` respectively. The temperature at `A,B,C` are `T_(1)=300K,T_(2)=600K` and `T_(3)=455K`. Indicate the pressure and volume at `A,B` and` C` by `P_(r)` and `V_(r), r=1,2,3,` respectively. Assume that intially pressure `P_(1)=1.00atm.`
Which of the following represents the correct values of the quantities indicated ?
View SolutionA reversible heat engine carries `1 mol` of an ideal monatomic gas around the cycle `ABCA`, as shown in the diagram. The process `BC` is adiabatic. Call the processes `AB, BC` and `CA` as `1,2` and `3` and the heat `( DeltaQ)_(r)`, change in internal energy `(DeltaU)`, and work done `( DeltaW)_(r), r=1,2,3` respectively. The temperature at `A,B,C` are `T_(1)=300K,T_(2)=600K` and `T_(3)=455K`. Indicate the pressure and volume at `A,B` and` C` by `P_(r)` and `V_(r), r=1,2,3,` respectively. Assume that intially pressure `P_(1)=1.00atm.`
Which of the following represents the correct values for the quantities indicated ?
View SolutionA reversible heat engine carries `1 mol` of an ideal monatomic gas around the cycle `ABCA`, as shown in the diagram. The process `BC` is adiabatic. Call the processes `AB, BC` and `CA` as `1,2` and `3` and the heat `( DeltaQ)_(r)`, change in internal energy `(DeltaU)`, and work done `( DeltaW)_(r), r=1,2,3` respectively. The temperature at `A,B,C` are `T_(1)=300K,T_(2)=600K` and `T_(3)=455K`. Indicate the pressure and volume at `A,B` and` C` by `P_(r)` and `V_(r), r=1,2,3,` respectively. Assume that intially pressure `P_(1)=1.00atm.`
Suppose the gas had been taken along an isothermal process from `B` instead of along the adiabatic process `BC` shown, so as to reach the same volume `V_(3)`, and the total heat `Q_(1)` is taken during the complete cycle involving the isothermal, while `Q_(a)` is the total heat taken in the cycle `ABCA` shown in the diagram. Then
View SolutionA monatomic ideal gas undergoes the shown cyclic process in which path of the process `2 rarr 3` is a semicircle. If `2 mol` of gas is taken, find

Heat given to the system in semicirculat process
View SolutionA monatomic ideal gas undergoes the shown cyclic process in which path of the process `2 rarr 3` is a semicircle. If `2 mol` of gas is taken, find

Total heat rejected in one cycle
View SolutionA gas take part in two thermal processes in which it is heated from the same initial state to the same final temperature. The processes are shown on the `P-V` diagram by straight lines `1 rarr 3 ` and `1 rarr 2`

View SolutionA gas take part in two thermal processes in which it is heated from the same initial state to the same final temperature. The processes are shown on the `P-V` diagram by straight lines `1 rarr 3 ` and `1 rarr 2`

View SolutionA monatomic idea gas of `2 mol` is taken through a cyclic process starting from `A` as shown in figure. The volume ratio are `V_(B)//V_(A)=2` and `V_(D)//V_(A)=4`. If the temperature `T_(A)` at `A` is `27^(@)C`, and gas constant is `R`. Calculate.
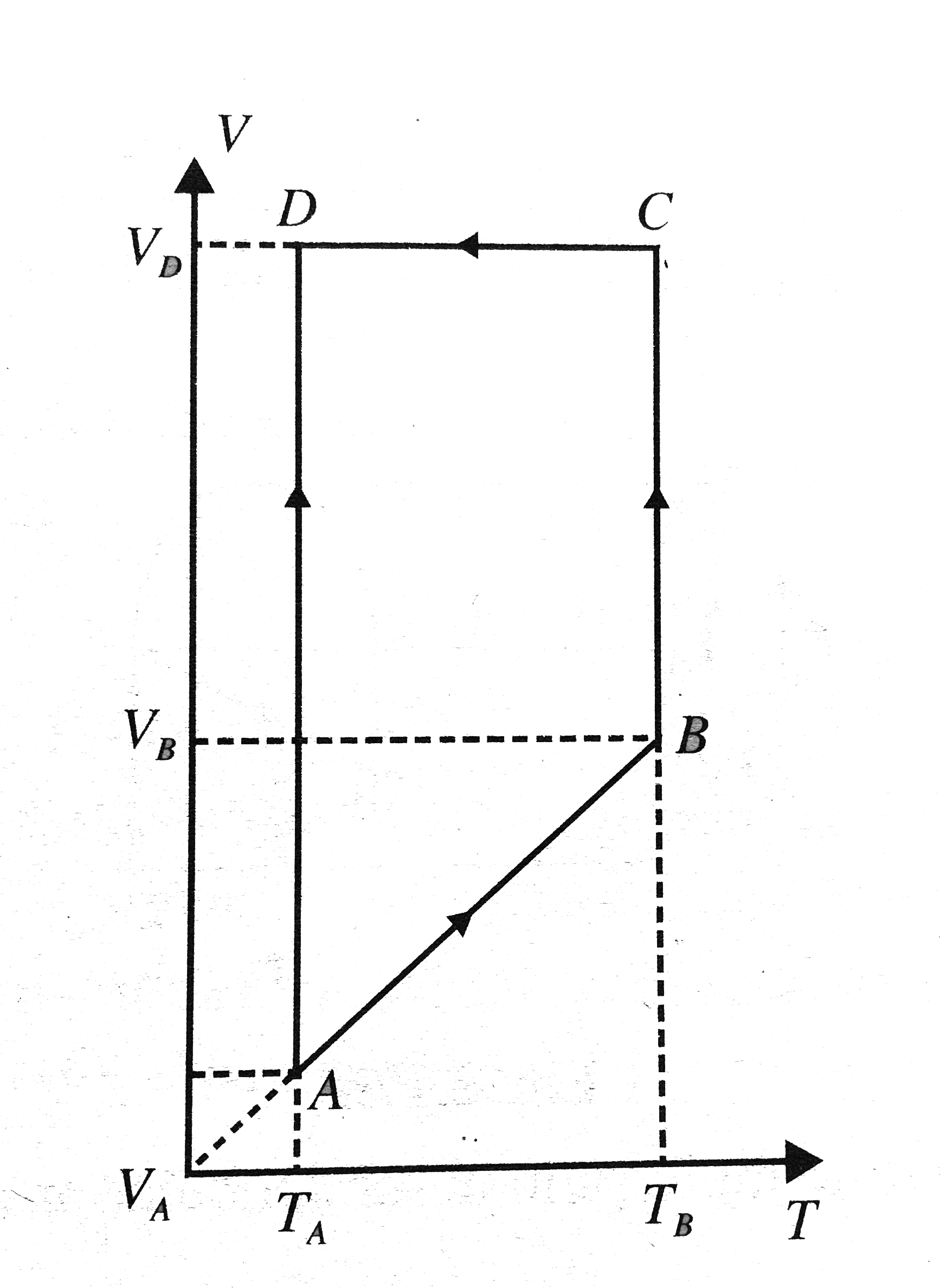
The temperature of the gas at point `B`
View SolutionA monatomic idea gas of `2 mol` is taken through a cyclic process starting from `A` as shown in figure. The volume ratio are `V_(B)//V_(A)=2` and `V_(D)//V_(A)=4`. If the temperature `T_(A)` at `A` is `27^(@)C`, and gas constant is `R`. Calculate.
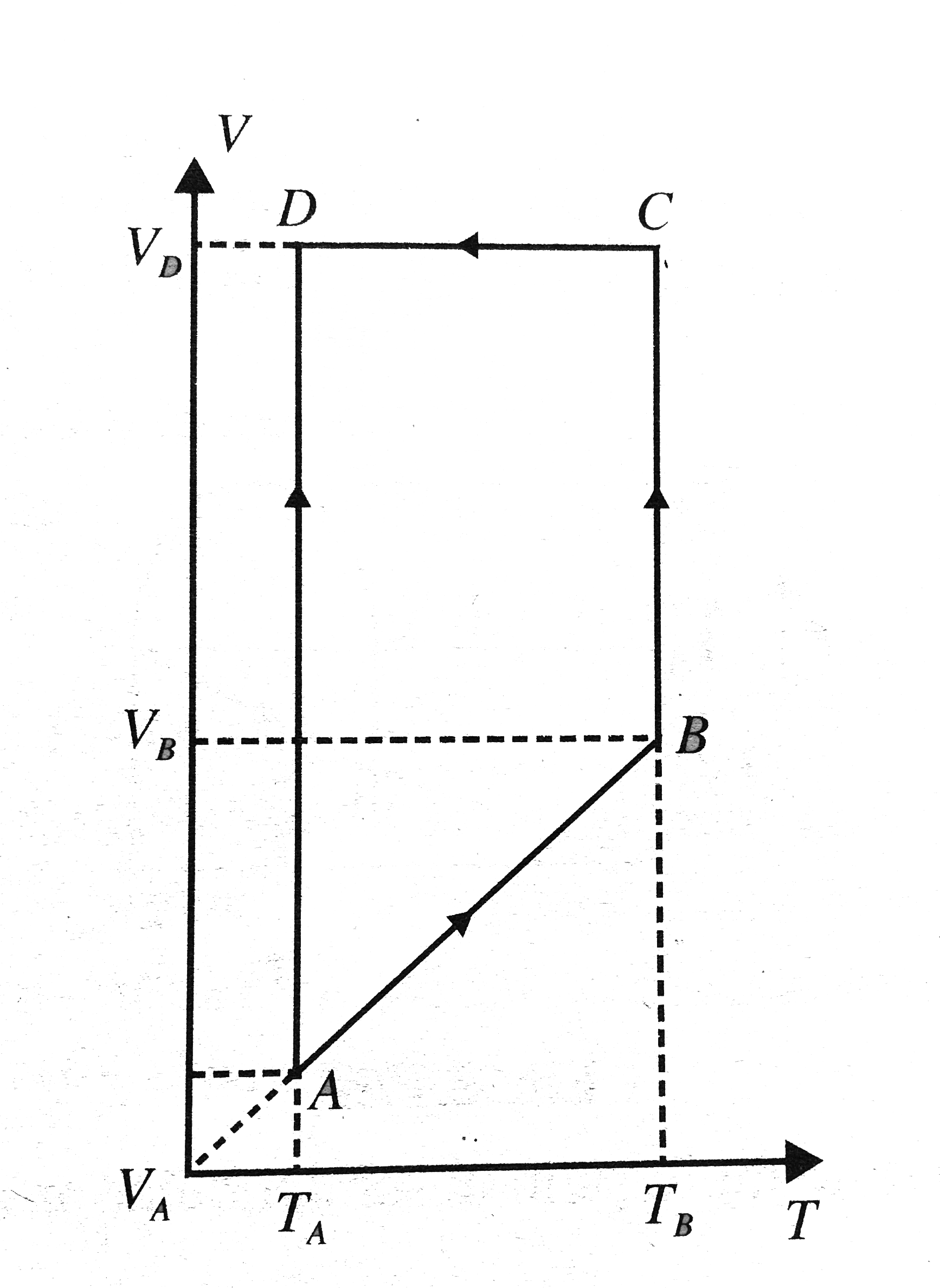
Heat absorbed or released by the gas in process `A rarr B`
View SolutionA monatomic idea gas of `2 mol` is taken through a cyclic process starting from `A` as shown in figure. The volume ratio are `V_(B)//V_(A)=2` and `V_(D)//V_(A)=4`. If the temperature `T_(A)` at `A` is `27^(@)C`, and gas constant is `R`. Calculate.
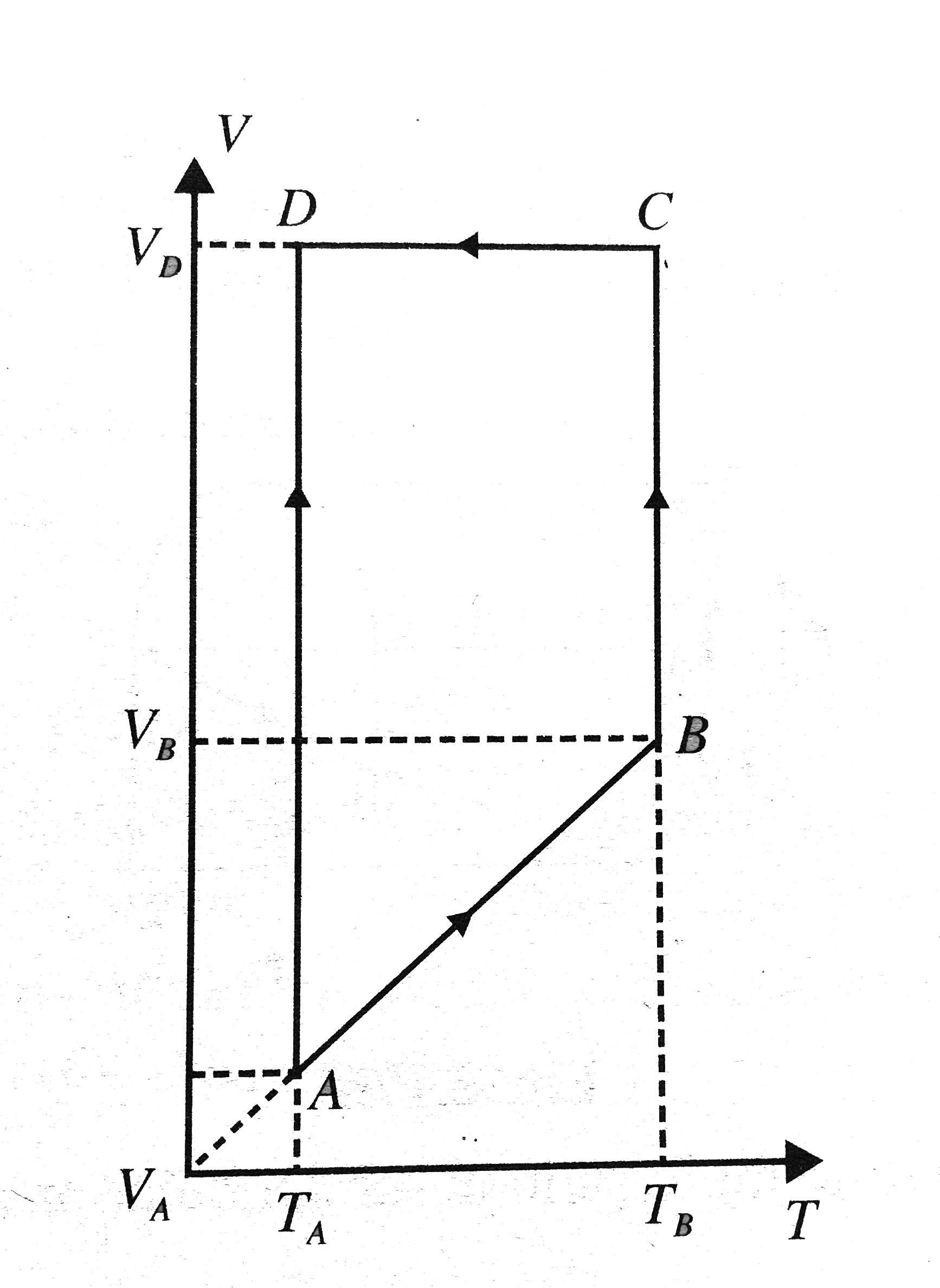 Heat absorbed or released by the gas in process `B rarr C`
Heat absorbed or released by the gas in process `B rarr C`
View SolutionA monatomic idea gas of `2 mol` is taken through a cyclic process starting from `A` as shown in figure. The volume ratio are `V_(B)//V_(A)=2` and `V_(D)//V_(A)=4`. If the temperature `T_(A)` at `A` is `27^(@)C`, and gas constant is `R`. Calculate.
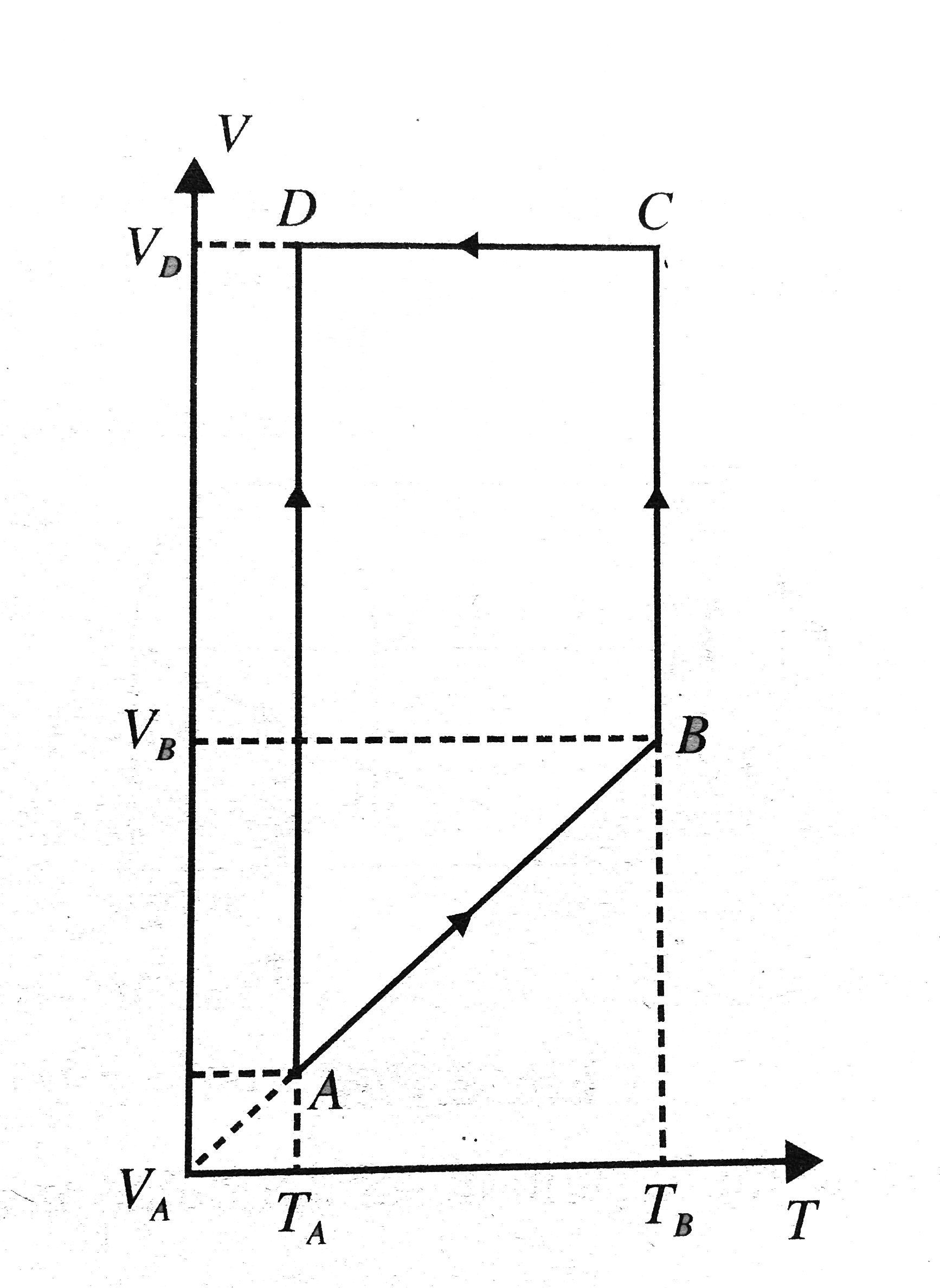
Heat absorbed or released by the gas in process `C rarr D`.
View SolutionA monatomic idea gas of `2 mol` is taken through a cyclic process starting from `A` as shown in figure. The volume ratio are `V_(B)//V_(A)=2` and `V_(D)//V_(A)=4`. If the temperature `T_(A)` at `A` is `27^(@)C`, and gas constant is `R`. Calculate.

Heat absorbed or released by the gas in procedd `D rarr A`.
View SolutionA monatomic idea gas of `2 mol` is taken through a cyclic process starting from `A` as shown in figure. The volume ratio are `V_(B)//V_(A)=2` and `V_(D)//V_(A)=4`. If the temperature `T_(A)` at `A` is `27^(@)C`, and gas constant is `R`. Calculate.
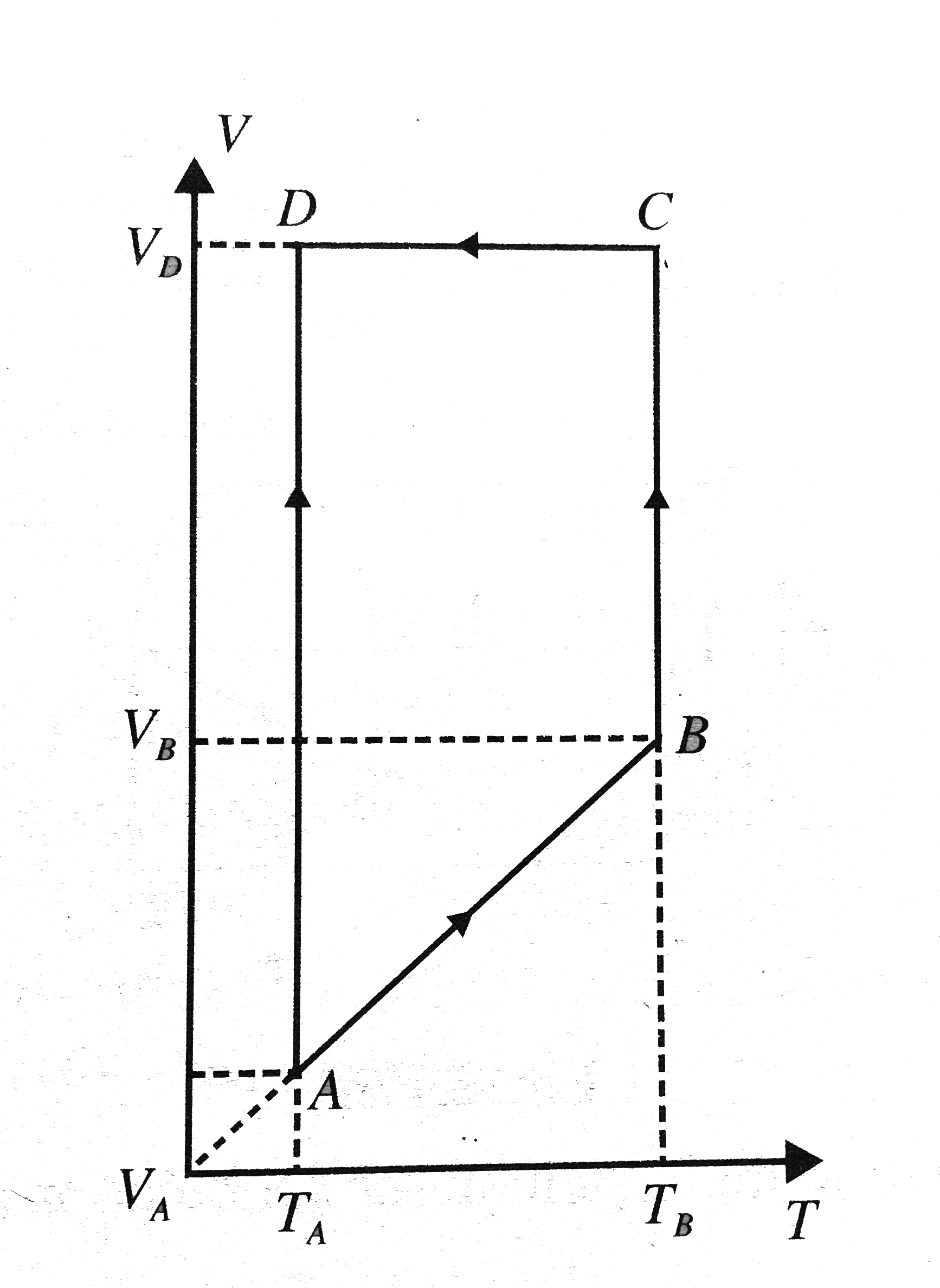
The total work done by the gas during the complete cycle.
View SolutionOne mole of an ideal monatomic gas udnergoes thermodynamic cycle `1 rarr 2 rarr 3 rarr 1` as shown in figure. Initial temperature of gas in `T_(0)=300K`.
Process ` 1 rarr2 : P=a V`
Process ` 2 rarr 3: PV=` Constant
Process `3 rarr 1 : P=` Constant
`(` Take `1n |3|=1.09)`
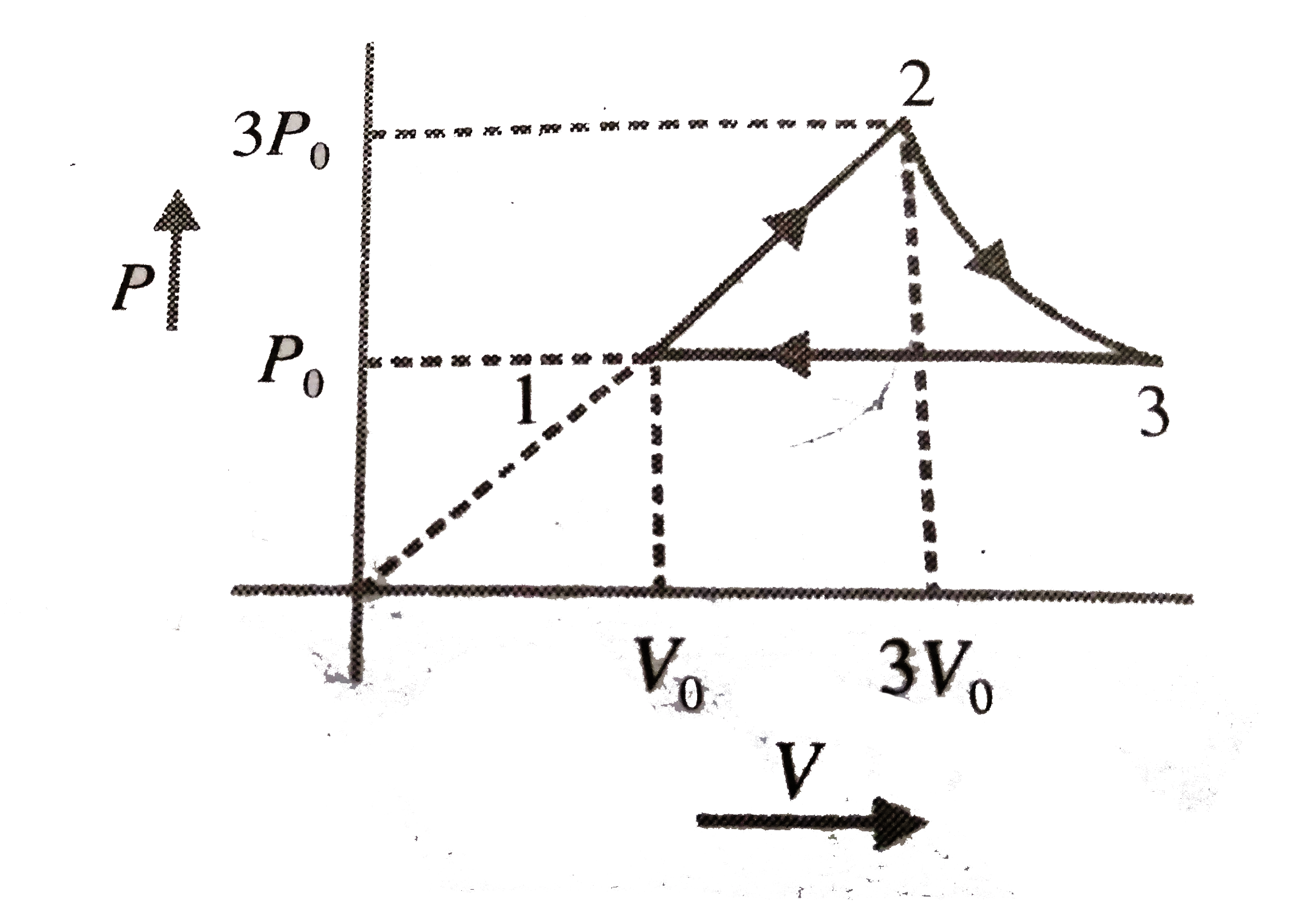
Find the net work done by the cycle.
View SolutionOne mole of an ideal monatomic gas udnergoes thermodynamic cycle `1 rarr 2 rarr 3 rarr 1` as shown in figure. Initial temperature of gas in `T_(0)=300K`.
Process ` 1 rarr2 : P=a V`
Process ` 2 rarr 3: PV=` Constant
Process `3 rarr 1 : P=` Constant
`(` Take `1n |3|=1.09)`
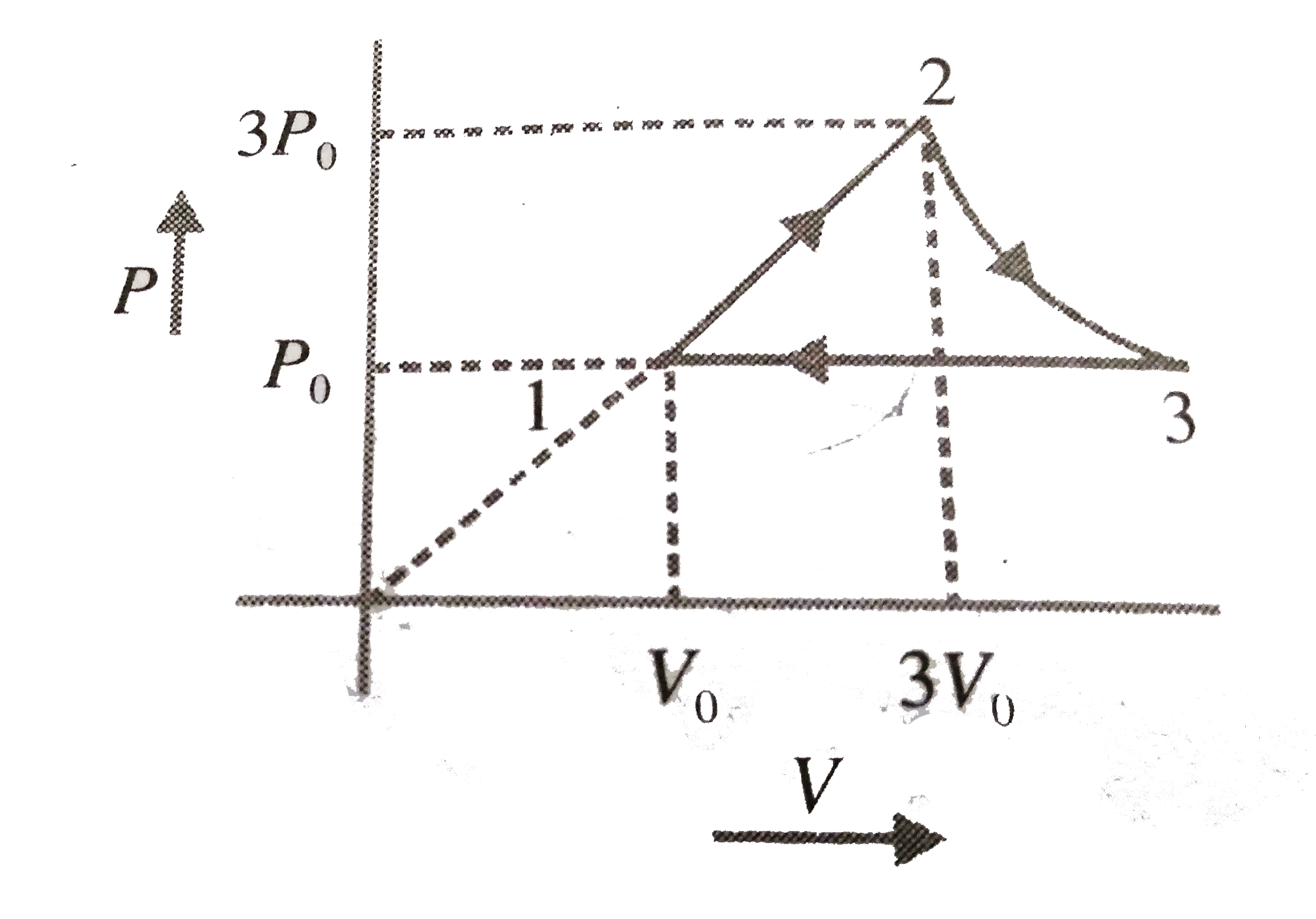
Determine the heat capacity of each process.
View SolutionA monatomic gas undergoes a cycle consisting of two isothermals and two isobarics. The minimum and maximum temperatures of gas during the cycle are `T_(1)= 400 K` and `T_(2)=800 K`, respectively, and the ratio of maximum to minimum volume is 4.
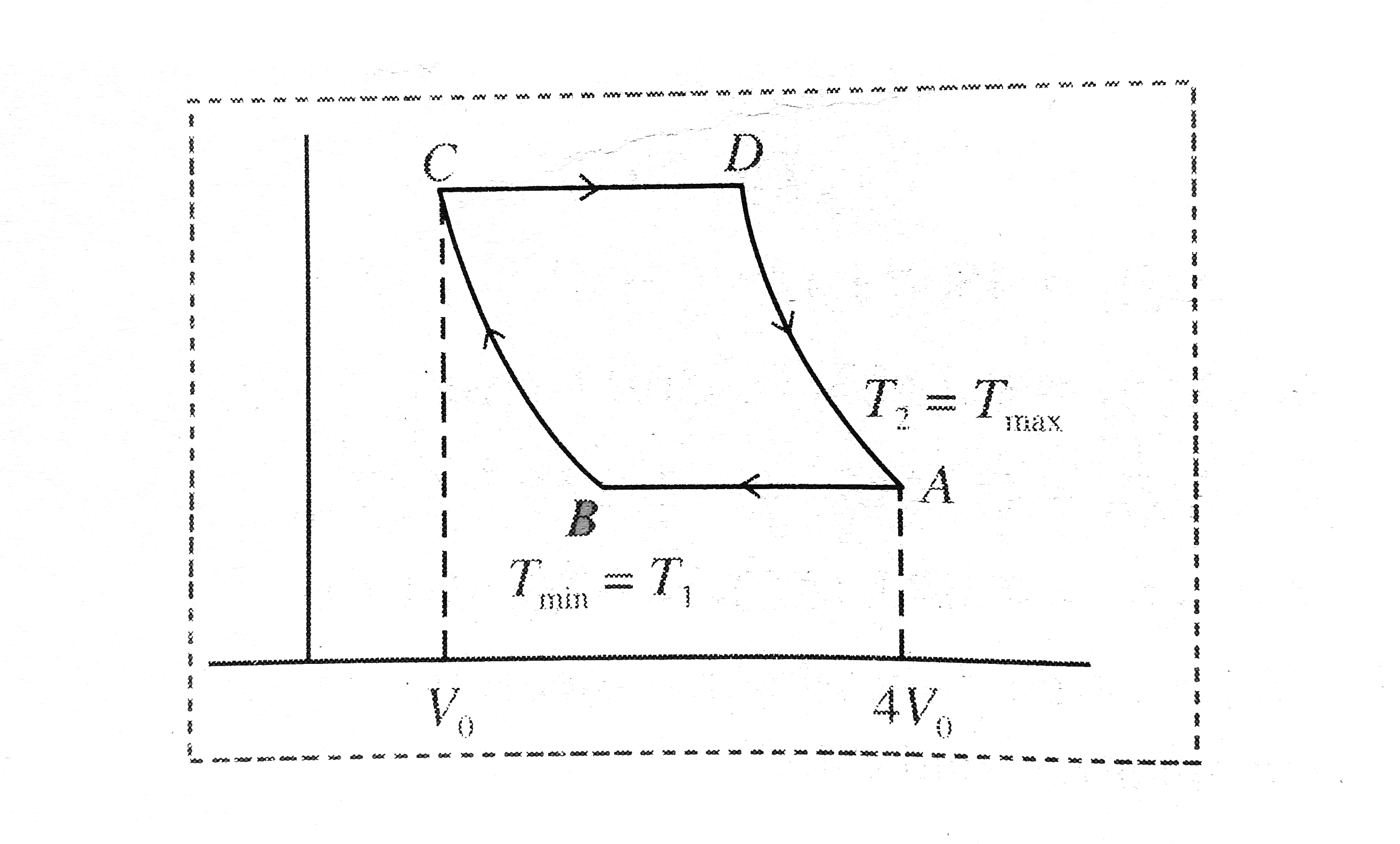
The volume at `B` is
View SolutionA monatomic gas undergoes a cycle consisting of two isothermals and two isobarics. The minimum and maximum temperatures of gas during the cycle are `T_(1)= 400 K` and `T_(2)=800 K`, respectively, and the ratio of maximum to minimum volume is 4.
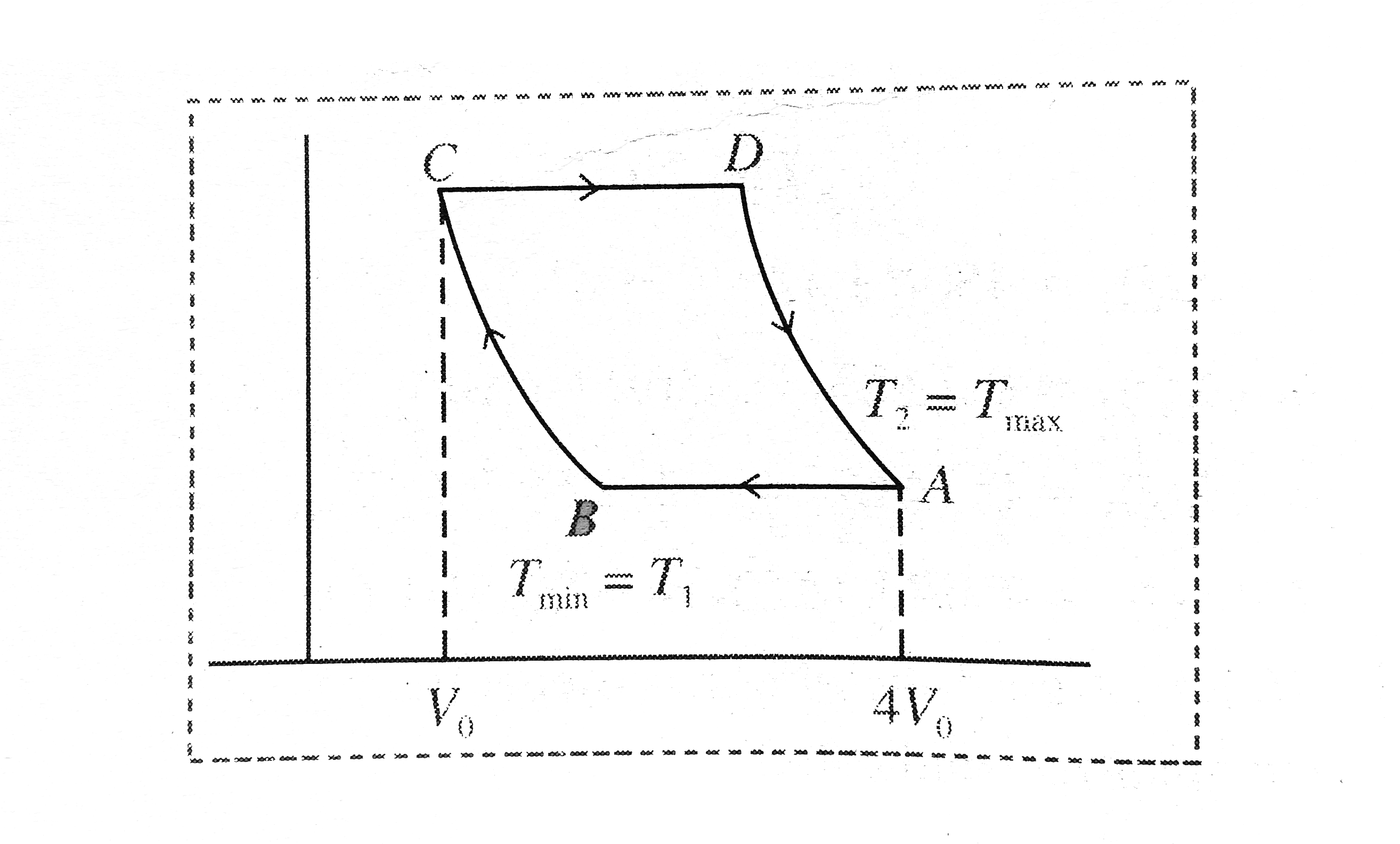
The volume is `D` is
View SolutionA monatomic gas undergoes a cycle consisting of two isothermals and two isobarics. The minimum and maximum temperatures of gas during the cycle are `T_(1)= 400 K` and `T_(2)=800 K`, respectively, and the ratio of maximum to minimum volume is 4.
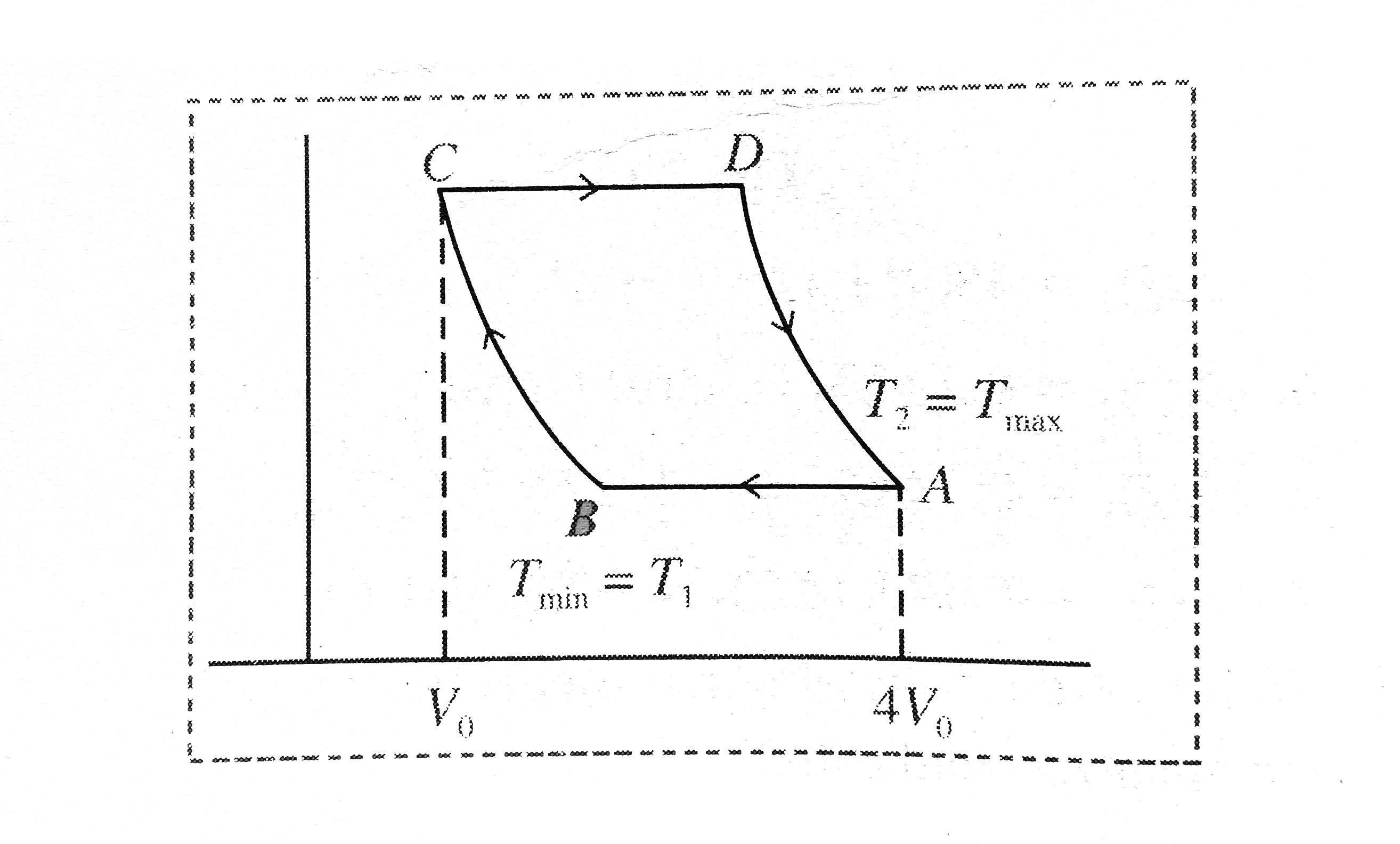
The heat is extracted from the system in process
View SolutionA monatomic gas undergoes a cycle consisting of two isothermals and two isobarics. The minimum and maximum temperatures of gas during the cycle are `T_(1)= 400 K` and `T_(2)=800 K`, respectively, and the ratio of maximum to minimum volume is 4.

The efficiency of the cycle is
View SolutionFigure shows an insulated cylinder of volume `V` containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final temperature
View SolutionFigure shows an insulated cylinder of volume `V` containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final pressures of left and right compartment respectively are
View SolutionFigure shows an insulated cylinder of volume `V` containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The heat that flows from `RHS` to `LHS`, Given `T_(2)gt T_(1)`.
Now, the pin which was keeping the piston fixed is removed. and the piston is set free to move. The piston is allowed to slide slowly, such that of mechanical equilibrium is also achieved and `T_(1)P_(2)gt P_(1)T_(2)`. Find.
View SolutionFigure shows an insulated cylinder of volume `V` containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.
View SolutionFigure shows an insulated cylinder of volume `V` containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of right compartment.
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas `(lambda=5//3)` at a pressure `P_0`, volume `V_0` and temperature `T_0`. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes `243P_0//32`. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
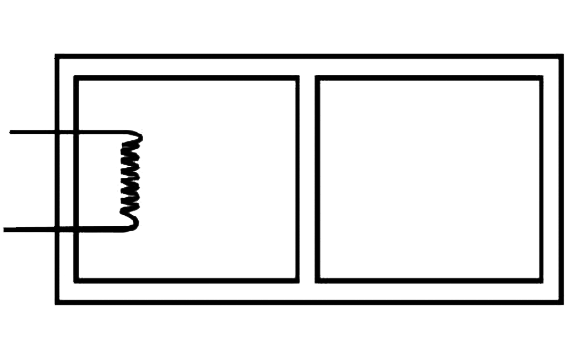
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas `(lambda=5//3)` at a pressure `P_0`, volume `V_0` and temperature `T_0`. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes `243P_0//32`. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.

View SolutionA container of volume `4V_(0)` made of a perfectly non`-` conducting material is divided into two equal parts by a fixed rigid wall whose lower half is non`-` conducting and upper half is purely conducting. The right side of the wall is divided into equal parts `(` initially `0` by means of a massless non`-` conducting piston free to move as shown . Section`A` constains `2 mol` of a gas while the section `B` and `C` contain ` 1 mol` each of the same gas `( gamma = 15. )` at pressure `P_(0)` . The heater in left part is switched on till the final pressure in section `C` becomes `125//27 P_(0)`. Calculate
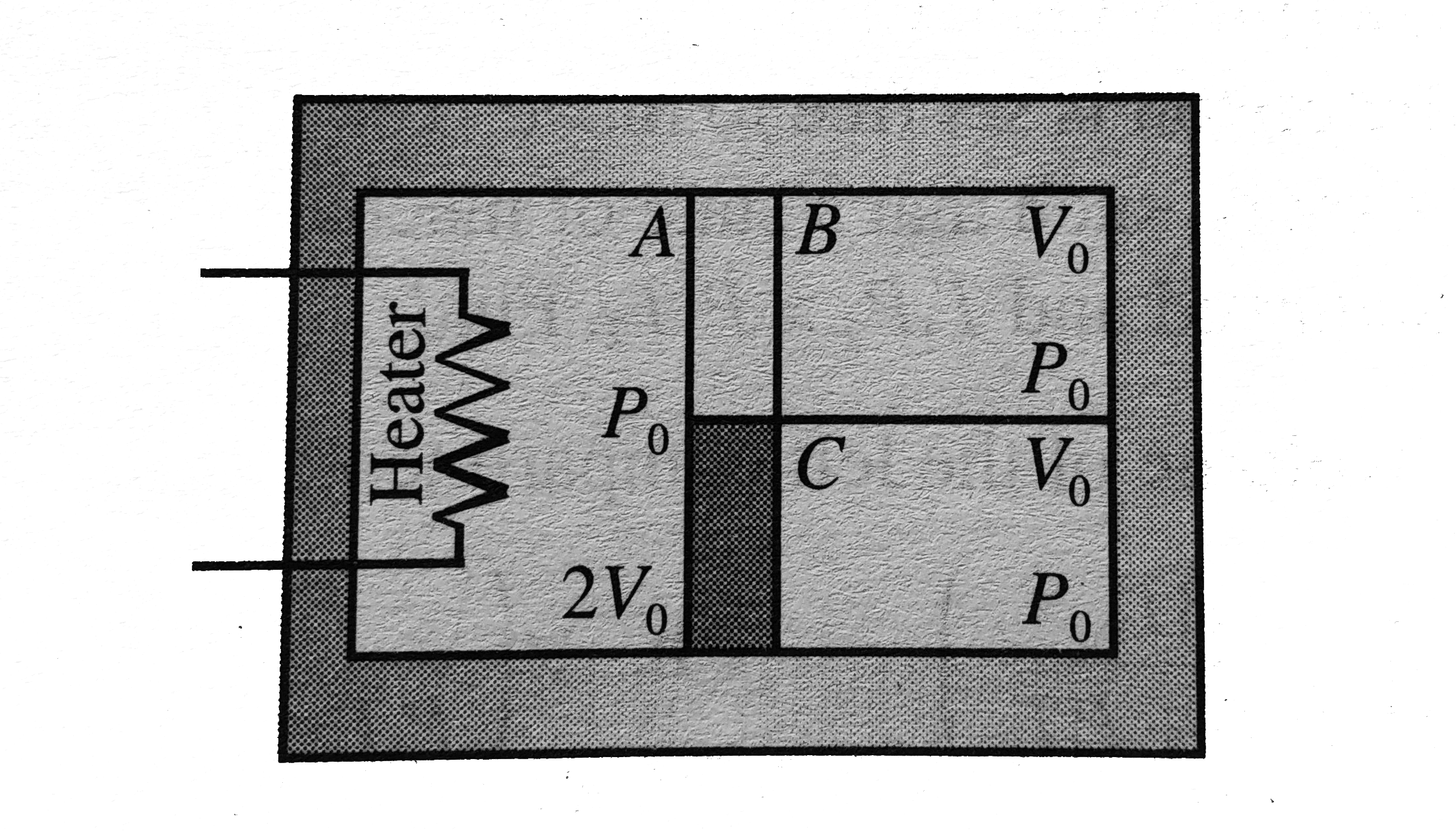
Final temperature in part `A`.
View SolutionA container of volume `4V_(0)` made of a perfectly non`-` conducting material is divided into two equal parts by a fixed rigid wall whose lower half is non`-` conducting and upper half is purely conducting. The right side of the wall is divided into equal parts `(` initially `0` by means of a massless non`-` conducting piston free to move as shown . Section`A` constains `2 mol` of a gas while the section `B` and `C` contain ` 1 mol` each of the same gas `( gamma = 15. )` at pressure `P_(0)` . The heater in left part is switched on till the final pressure in section `C` becomes `125//27 P_(0)`. Calculate
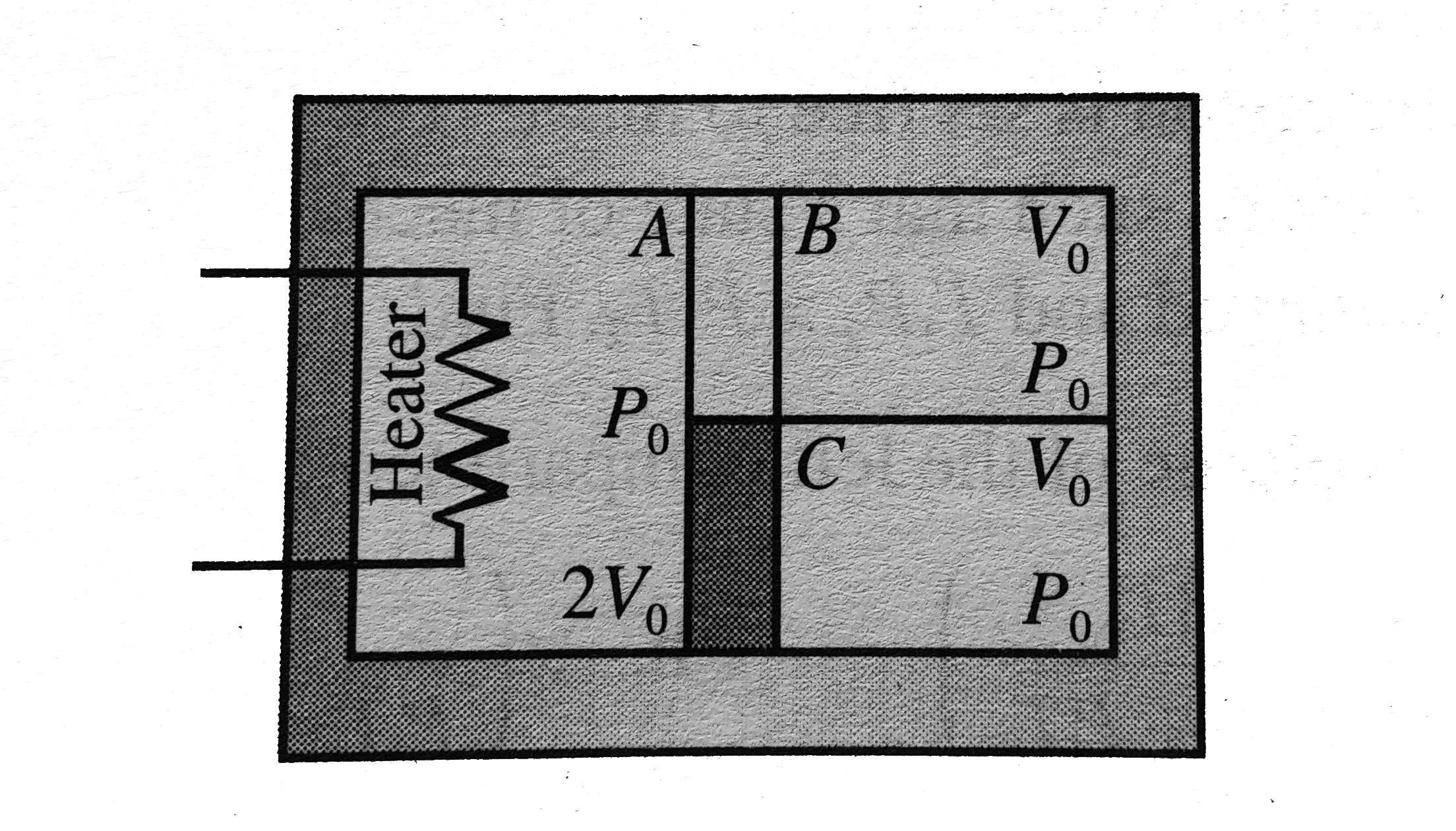
Final temperature in part `C`.
View SolutionA container of volume `4V_(0)` made of a perfectly non`-` conducting material is divided into two equal parts by a fixed rigid wall whose lower half is non`-` conducting and upper half is purely conducting. The right side of the wall is divided into equal parts `(` initially `0` by means of a massless non`-` conducting piston free to move as shown . Section `A` contains `2 mol` of a gas while the section `B` and `C` contain ` 1 mol` each of the same gas `( gamma = 15. )` at pressure `P_(0)` . The heater in left part is switched on till the final pressure in section `C` becomes `125//27 P_(0)`. Calculate
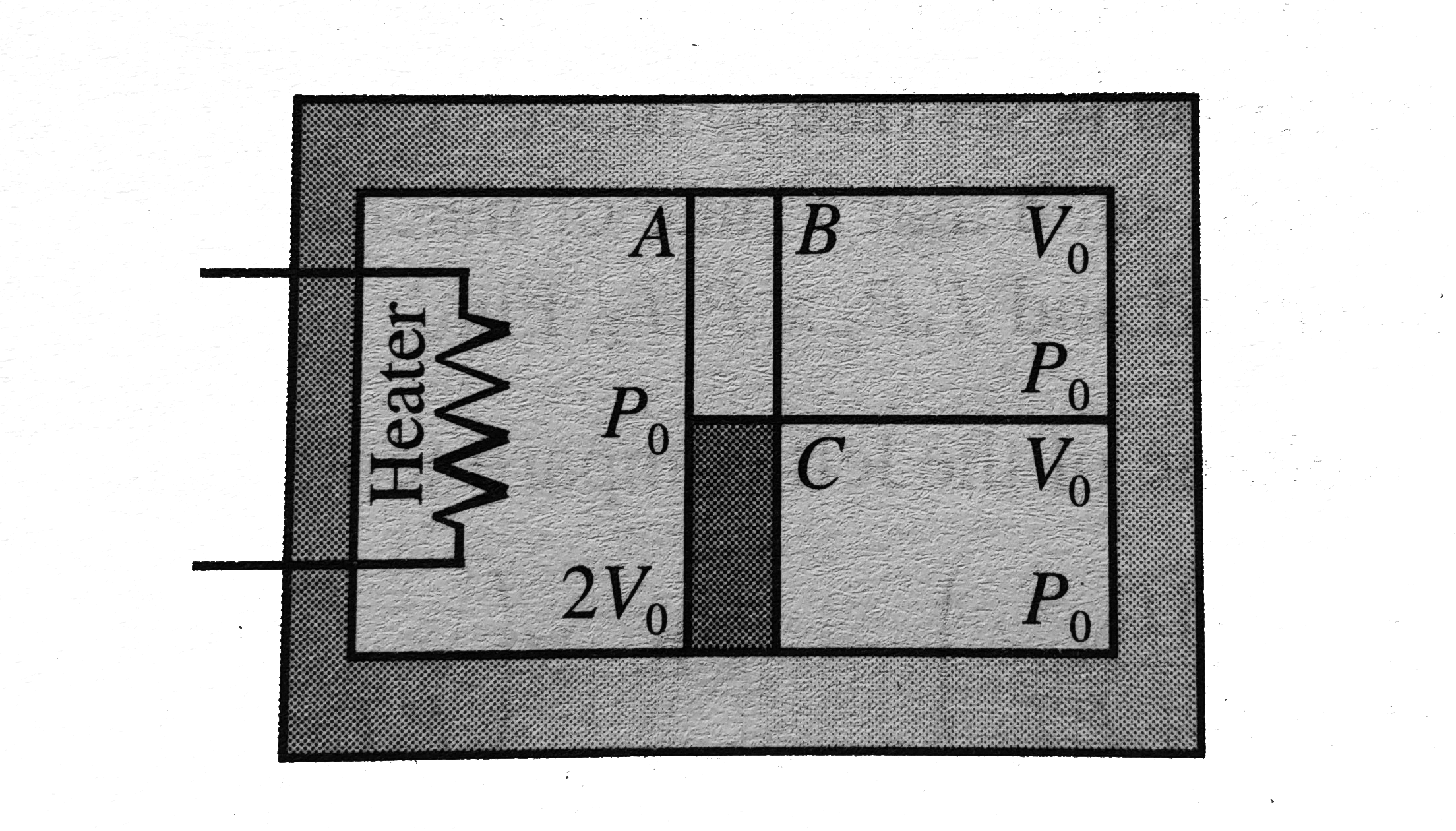
The heat supplied by the heater.
View SolutionAn ideal gas at `NTP` is enclosed in an adiabatic vertical cylinder havin an area of cross section `A=27 cm^(2)` between two light movable pistons as shown in figure. Spring with force constant `K=37-- N//m` is in a relaxed state initially. Now the lower position is moved upwards a distance `h//2`, `h` being the initial length of gas column . It is observed that the upper piston moves up by a distance `h//16`. Final temperature of gas` 4//3 xx 273 K`. Take `gamma` for the gas to be `3//2`.

When the lower pistone is moved upwards a distance `h//2`, the compression.
View SolutionAn ideal gas at `NTP` is enclosed in an adiabatic vertical cylinder havin an area of cross section `A=27 cm^(2)` between two light movable pistons as shown in figure. Spring with force constant `K=37-- N//m` is in a relaxed state initially. Now the lower position is moved upwards a distance `h//2`, `h` being the initial length of gas column . It is observed that the upper piston moves up by a distance `h//16`. Final temperature of gas` 4//3 xx 273 K`. Take `gamma` for the gas to be `3//2`.

Which of the following statements is correct ?
View SolutionAn ideal gas at `NTP` is enclosed in an adiabatic vertical cylinder havin an area of cross section `A=27 cm^(2)` between two light movable pistons as shown in figure. Spring with force constant `K=37-- N//m` is in a relaxed state initially. Now the lower position is moved upwards a distance `h//2`, `h` being the initial length of gas column . It is observed that the upper piston moves up by a distance `h//16`. Final temperature of gas` 4//3 xx 273 K`. Take `gamma` for the gas to be `3//2`.

The value of `h` is
View SolutionPiston cylinder device initially contains `0.5m^(3)` of nitrogen gas at `400 kPa` and `27^(@)C`. An electric heater within the device is turned on and is allowed to apss a current of `2 A` for `5 mi n` from a `120 V` source. Nitrogen expands at constant pressure and a heat loss of `2800 J` occurs during the process.
`R=25//3 kJ //k mol - K`
Electric work done on the nitrogen gas is
View SolutionPiston cylinder device initially contains `0.5m^(3)` of nitrogen gas at `400 kPa` and `27^(@)C`. An electric heater within the device is turned on and is allowed to apss a current of `2 A` for `5 mi n` from a `120 V` source. Nitrogen expands at constant pressure and a heat loss of `2800 J` occurs during the process.
`R=25//3 kJ //k mol - K`
Number of moles of nitrogen gas is
View SolutionPiston cylinder device initially contains `0.5m^(3)` of nitrogen gas at `400 kPa` and `27^(@)C`. An electric heater within the device is turned on and is allowed to pass a current of `2 A` for `5 mi n` from a `120 V` source. Nitrogen expands at constant pressure and a heat loss of `2800 J` occurs during the process.
`R=25//3 kJ //k mol - K`
The final temperature of nitrogen is
View Solution
Comprehension questions and complete solutions for chapter KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS of CENGAGE PHYSICS (HINGLISH) of Class 11