Complete Solutions to Single Correct of chapter KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The temperature of a gas is raised while its volume remains constant, the pressure exerted by the gas on the walls of the container increases because its molecules
View SolutionA cylinder of capacity `20 L` is filled with `H_(2)` gas. The total average kinetic energy of translatory motion of its molecules is `1,5 xx 10^(5) J`. The pressure of hydrogen in the cylinder is
View SolutionA flask is filled with `13 g` of an ideal gas at `27^(@)C` and its temperature is raised to `52^(@)C`. The mass of the gas that has to be released to maintain the temperature of the gas in the flask at `52^(@)C`, the pressure remaining the same is
View SolutionAir is filled at `60^(@)C` in a vessel of open mouth. The vessle is heated to a temperature `T` so that `1//4th` of air escapes. Assuming the volume of vessel remaining constant, the value of `T` is
View SolutionIf the intermolecules forces vanish away, the volume occupied by the molecules contained in `4.5 kg` water at stantard temperature and pressure will be given by
View SolutionThe expansion of an ideal gas of mass `m` at a constant pressure `P` is given by the straight line `D`. Then the expanison of the same ideal gas of mass `2m` at a pressure `P//2` is given by the straight line

View SolutionTwo containers of equal volume contain the same gas at pressure `P_(1)` and `P_(2)` and absolute temperature `T_(1)` and `T_(2)`, respectively. On joining the vessels, the gas reaches a common pressure `P` and common temperature `T`. The ratio `P//T` is equal to
View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section `8.0xx10^-3m^2`. Initially the gas is at 300K and occupies a volume of `2.4xx10^-3m^3` and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is `8000 N//m`, atmospheric pressure is `1.0xx10^5 Nm^-2`. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionA box contains `N` molecules of a perfect gas at temperature `T_(1)` and temperature `P_(1)`. The number of molecule in the box is double keeping the total kinetic energy of the gas same as before. If the new pressure is `P_(2)` and temperature `T_(2), then
View SolutionA gas is filled in the cylinder shown in fig. The two pistons are joined by a string. If the gas is heated, the right piston will
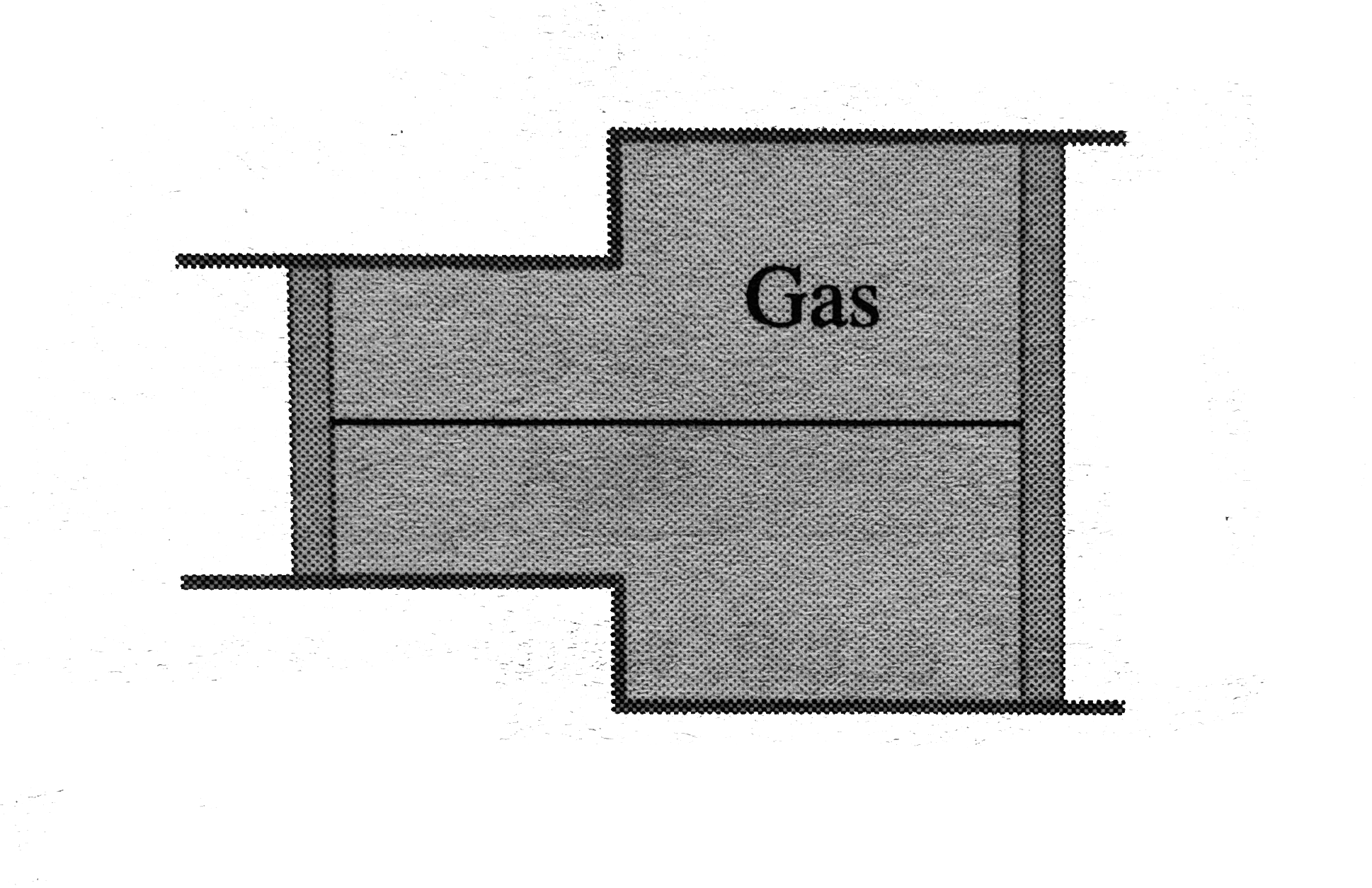
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by `DeltaV` due to an increase in temperature `DeltaT,` pressure remaining constant. The quantity `delta=(DeltaV)/(VDeltaT)` varies with temperature as
View SolutionThe pressure of a gas filled in a closed vessel increase by 0.4% when temperature is increased by `1^(@) C`. Find the initial temperature of the gas.
View SolutionPressure versus temperature graph of an ideal gas of equal number of moles of different volumes is plotted as shown in Fig. Choose the correct alternative.
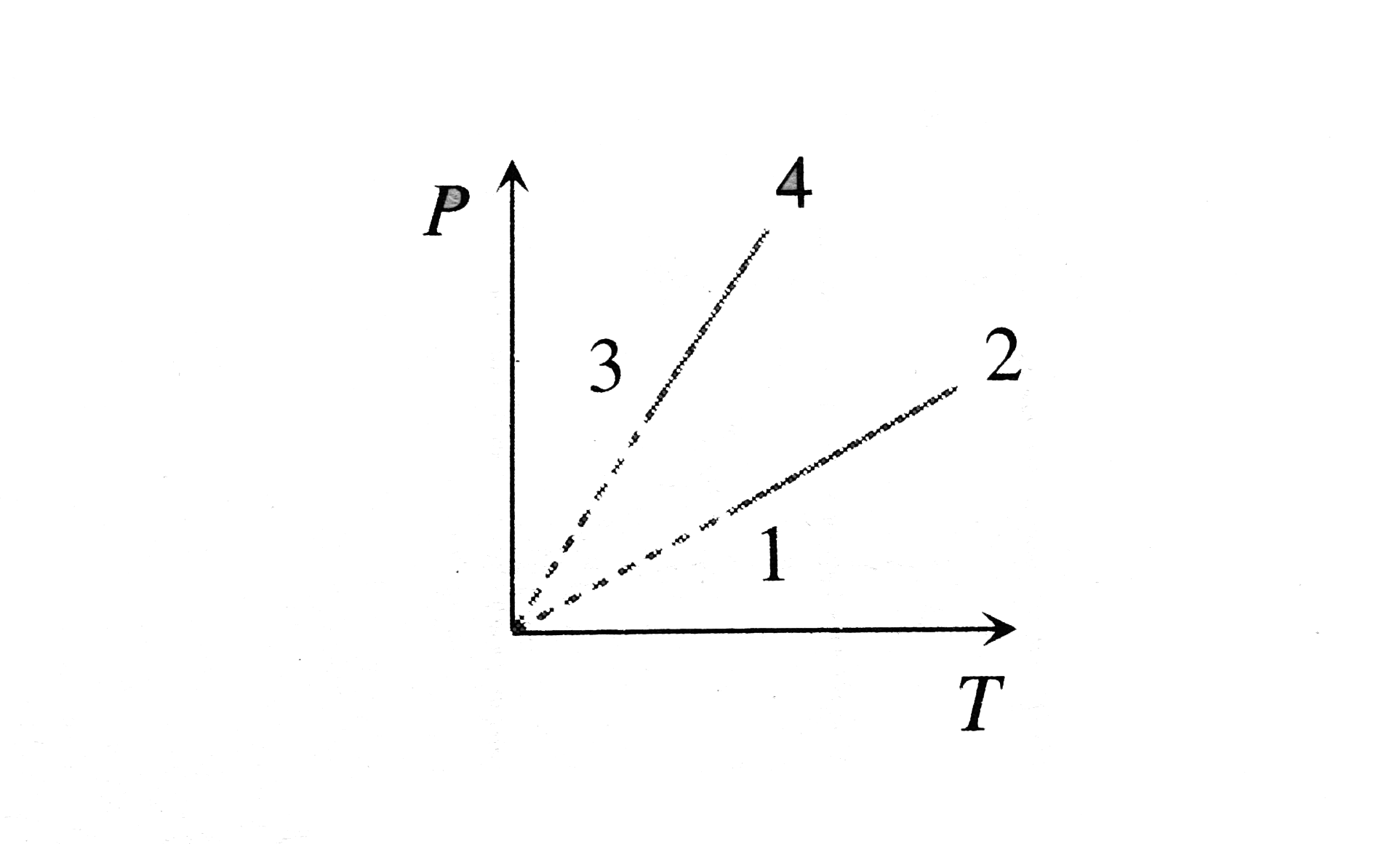
View SolutionThe capacity of a vessel is `3 L`. It contains `6 g` oxygen, `8 g` nitrogen and `5 g CO_(2)` mixture at `27^(@)C`, If `R = 8.31 J//mol K`, then the pressure in the vessel in `N//m^(2)` will be (approx.)
View SolutionTwo gases occupy two containers `A` and `B` then gas in `A`, of volume `0.10 m^(3)`, exerts a pressure of `1.40 Mpa` and that in `B`, of volume `0.15 m^(3)`, exerts a pressure `0.7 MP a`. The two containers are joined by a tube of negligible volume and the gases are allowed to intermingle. Then if the temperature remains constant, the final pressure in the container will be (in MPa)
View SolutionA closed vessel contains `8 g` of oxygen and ` 7 g` of nitrogen. The total pressure is 10 atm at a given temperature. If now oxygen is absorbed by introducing a suitable absorbent, the pressure of the remaining gas in atm will be
View SolutionEnergy of all molecules of a monatomic gas having a volume `V` and pressure `P` is `3//2 PV`. The total translational kinetic energy of all molecules of a diatomic gas at the same volume and pressure is
View SolutionForty calories of heat is needed to raise the temperature of 1 mol of an ideal monatomic gas from `20^(@)C` to `30^(@)C` at a constant pressure. The amount of heat required to raise its temperature over the same interval at a constant volume `(R = 2 cal mol^(-1) K^(-1))` is
View SolutionFor a gas the differce between the two specific heat is `4150 J//kg K`. What is the specific heat at constant volume of gas if the ratio of sepcific heat is 1.4
View SolutionThe sepific heat at constant volume for the monatomic argon is `0.075 kcal//kg-K`, whereas its gram molecular specific heat is `C_(V) = 2.98 cal//mol//K`. The mass of the argon atom is (Avogadro's number `= 6.02 xx 10^(23) "molecules"//"mol")
View SolutionThe temperature of `5 mol` of gas which was held at constant volume was change from `100^(@)C` to `120^(@)C`. The change in internal energy was found to ve `80 J`. The total heat capacity of the gas at constant volume will be equal to
View SolutionA gas is heated at a constant pressure. The fraction of heat supplied used of external work is
View SolutionA monatomic gas expands at constant pressure on heating. The percentage of heat supplied that increases the internal energy of the gas and that is involed in the expansion is
View SolutionThe average degrees of freedom per molecule for a gas are 6. The gas performs `25 J` of work when it expands at constant pressure. The heat absorbed by gas is
View SolutionCertain amount of an ideal gas is contained in a closed vessel. The vessel is moving with a constant velcity `v`. The molecular mass of gas is `M`. The rise in temperature of the gas when the vessel is suddenly stopped is `(gamma C_(P) // C_(V))`
View SolutionThe density of a polyatomic gas in stantard conditions is `0.795 kg m^(-3)`. The specific heat of the gas at constant
View SolutionThe value of `C_(P) - C_(v) = 1.00 R` for a gas in state `A` and `C_(P) - C_(v) = 1.06 R` in another state. If `P_(A)` and `P_(B)` denote the pressure and `T_(A)` and `T_(B)` denote the temperature in the two states, then
View SolutionWhen 1 mole of monoatomic gas is mixed with 2 moles of diatomic gas, then find `C_(P), C_(v), f and gamma` for the mixture of gases.
View SolutionTwenty-two grams of `CO_(2)` at `27^(@)C` is mixed with `16 g` of `O_(2)` at `37^(@)C`. The temperature of the mixture is about
View SolutionA gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
View SolutionA thermodynamic system is taken through the cyclic `PQRSP` process. The net work done by the system is

View SolutionAnideal gas is taken around `ABCA` as shown in the above `P-V` diagram. The work done during a cycle is
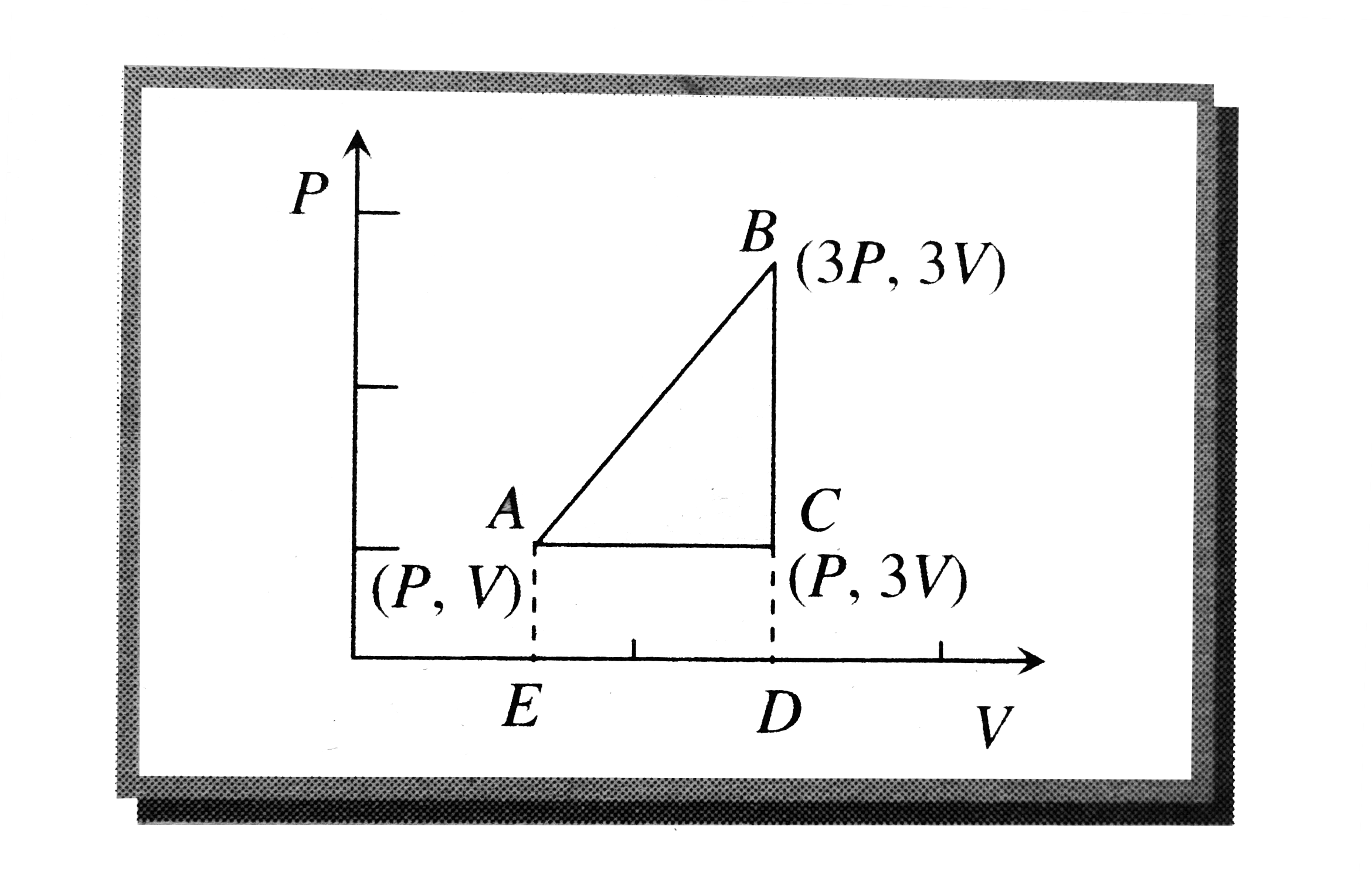
View SolutionAn ideal gas of mass `m` in a state `A` goes to another state `B` via three different processes as shown in Fig. If `Q_(1), Q_(2)` and `Q_(3)` denote the heat absorbed by the gas along the three paths, then

View SolutionThe relation between the internal energy `U` adiabatic constant `gamma` is
View SolutionA thermodynamic process is shown in Fig. The pressures and volumes corresponding to some points in the figure are : `P_(A) = 3 xx 10^(4) Pa, P_(B) = 8 xx 10^(4) Pa` and `V_(A) = 2 xx 10^(-3) m^(3) , V_(D) = 5 xx 10^(-3) m`.
In process `AB, 600 J` of heat is added to the system and in process `BC, 200 J` of heat is added to the system. The change in internal energy of the energy of the process `AC` would be.

View SolutionIf `R = ` universal gas constant, the amount of heat needed to raise the temperature the temperature of `2 mol` of an ideal monatomic gas from `273 K` to `373 K` when no work is done is
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
View SolutionAn ideal gas at `27^(@)C` is compressed adiabatically to `8//27` of its original volume. If `gamma = 5//3`, then the rise in temperature is
View SolutionFour curves `A, B, C` and `D` are drawn in Fig. for a given amount of gas. The curves which represent adabatic and isothermal changes

View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are `P` and `T` for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionTwo sample `A` and `B` of a gas initially at the square at the same pressure and temperature are compressed from volume `V` to `V//2` (A isothermally and `B` adiabatically). The final pressure of `A` is
View Solution`1 cm^(3)` of water at its boiling point absorbs `540 cal` of heat to become steam with a volume of `1671 cm^(3)`. If the atmospheic pressure is `1.013 xx 10^(5) N//m^(2)` and the mechanical equivalent of heat `= 4.19 J//cal`, the energy spent in this process in overcoming intermolecular forces is
View SolutionFive moles of hydrogen gas are heated from `30^(@)C` to `60^(@)C` at constant pressure. Heat given to the gas is (given `R = 2 cal//mol` degrees)
View SolutionWhen an ideal gas `(gamma = 5//3)` is heated under constant pressure, what percentage of given heat energy will be utilized in doing external work ?
View SolutionAt `100^(@)C` the volume of `1 kg` of water is `10^(-3) m^(3)` and volume of `1 kg` of steam at normal pressure is `1.671 m^(3)`. The latent heat of steam is `2.3 xx 10^(6) J//kg` and the normal pressure is `10^(5) N//m^(2)`. If `5 kg` of water at `100^(@)C` is converted into steam, the increase in the internal energy of water in this process will be
View SolutionIn the following pressure-volume diagram, the isochoric, isothermal and isobaric parts, respectively, are

View SolutionThe `P-V` diagram of a system undergoing thermodynnaic transformation is shown in Fig. The work done on the system in going from `A rarr B rarr C` is `50 J` and `20 cal` heat is given to the system. The change in internal erergy between `A` and `C` is

View SolutionIn the following indicator diagram, the net amount of work done will be

View SolutionThe cyclic process for 1 mole of an ideal gas is shown in the V-T diagram. The work done in AB, BC and CA respectively is

View SolutionA cyclic process `ABCD` is shown is shown in the following `P-V` diagram. Which of the following curves represent the same process ?

View SolutionAn ideal gas expands in such a manner that its pressure and volume can be related by equation `PV^(2) = ` constant. During this process, the gas is
View SolutionA cyclic process `ABCA` is shown in the `V-T` diagram process on the `P-V`

View SolutionOne mole of a diatomic gas undergoes a process `P = P_(0)//[1 + (V//V_(0)^(3))]` where `P_(0)` and `V_(0)` are constant. The translational kinetic energy of the gas when `V = V_(0)` is given by
View SolutionIf `50 cal` of heat is supplied to the system containing `2 mol` of an ideal monatomic gas, the rise in temperature is `(R = 2 cal//mol-K)`

View SolutionIn the given elliptical `P-V` diagram
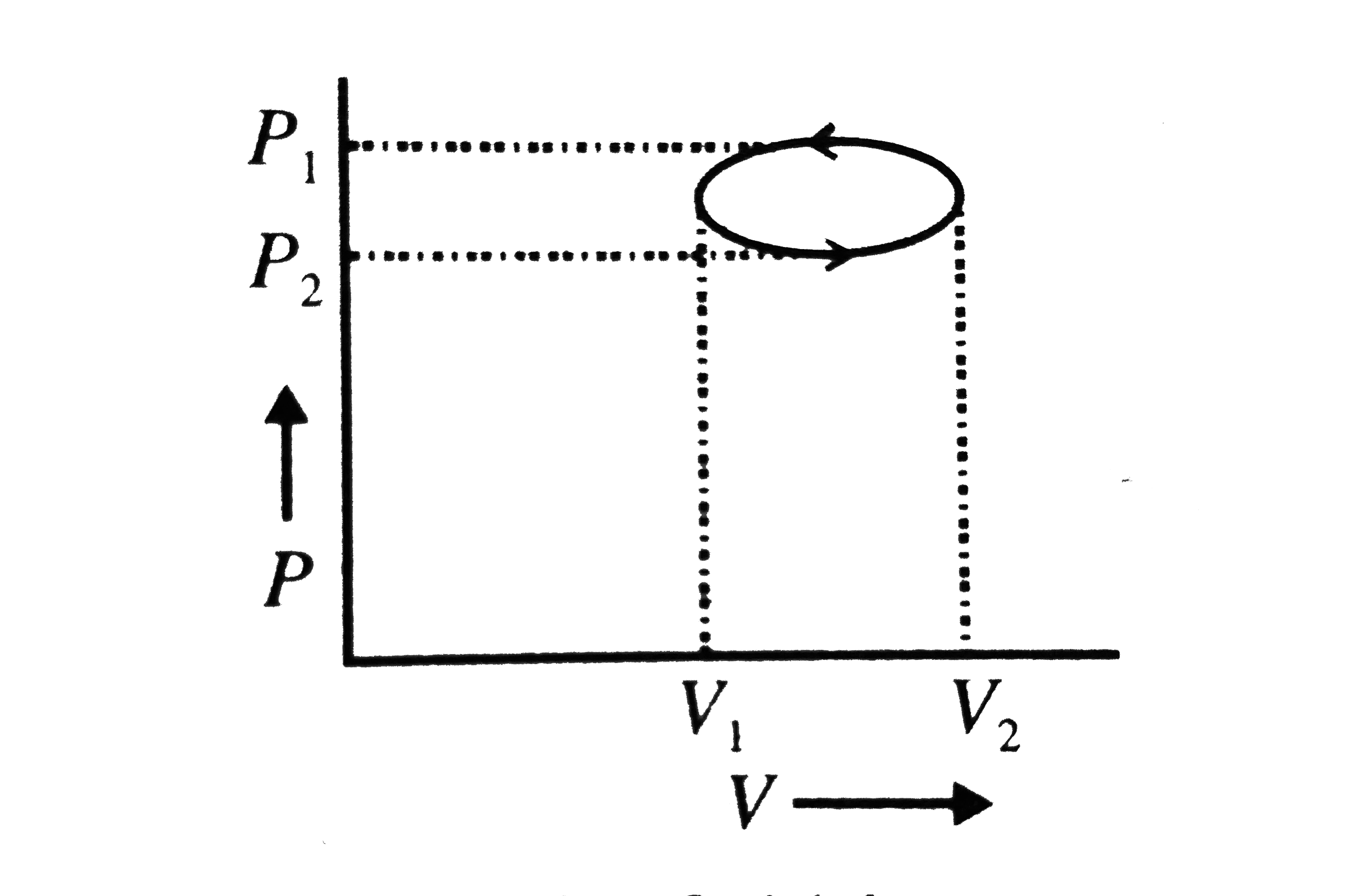
View SolutionThree processes compose a thermodynamic cycle shown in the accompanying `P-V`, diagram of an ideal gas.
Process `1 rarr 2` take place at constant temperature, during this process `60 J` of heat enters the system.
Process `2 rarr 3` takes place at constant volume. During this process `40 J` of heat leaves the system.
Process `3 rarr 1` is adiabatic.
What is the change in internal energy of the during process `3 rarr 1`?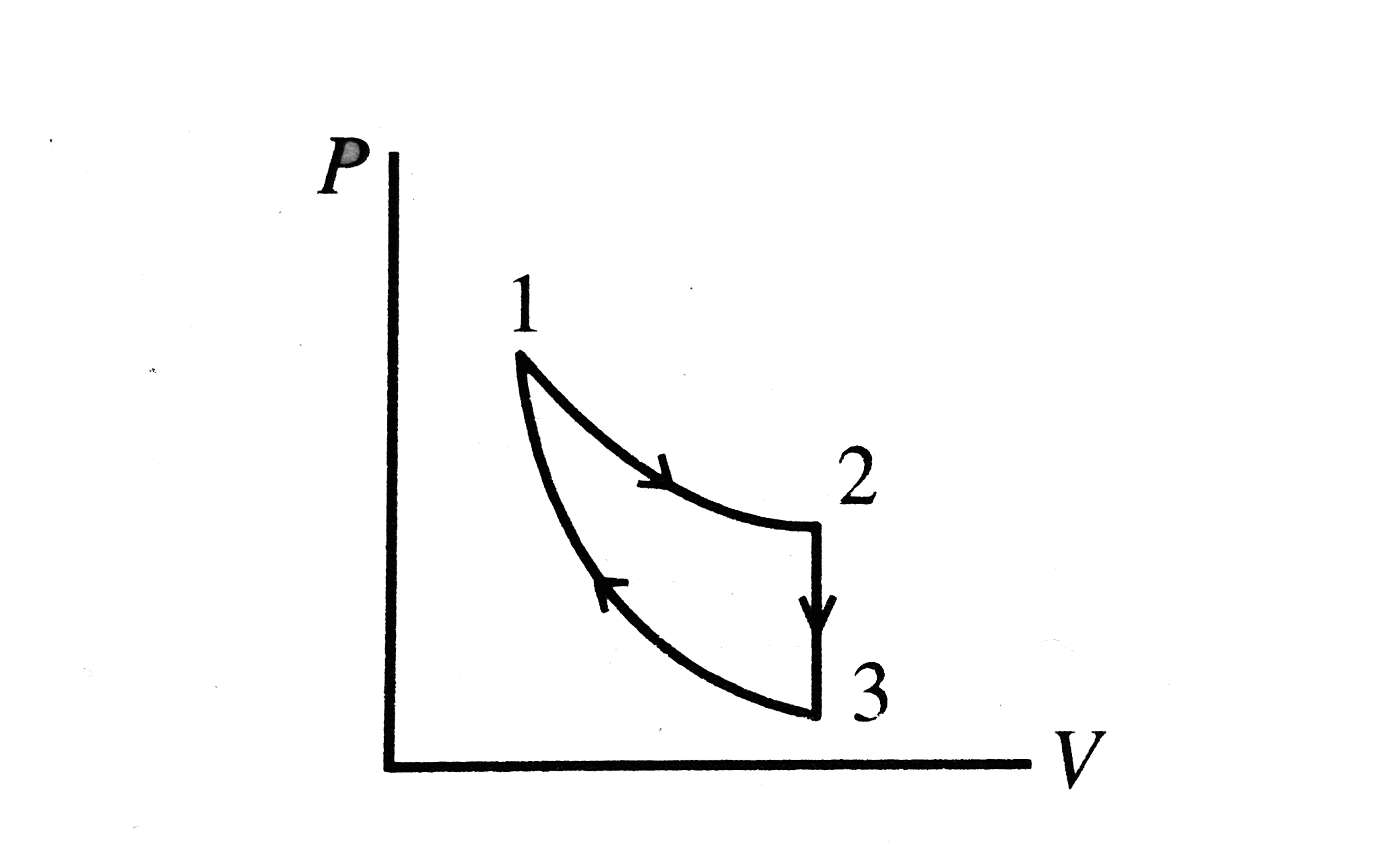
View SolutionWhen an ideal gas is taken from state `a` to `b`, along a path `acb, 84 kJ` of heat flows into the gas and the gas does `32 kJ` of work. The following conclusions are drawn. Mark the one which is not correct.

View SolutionA sample of an ideal gas is taken through the cyclic-process `ABCA` shown in Fig. It rejects `50 J` of heat during the part `AB`, doens not absorb or reject the heat during `BC`, and accepts `70 J` of heat during `CA`. Forty joules of works is done on the gas during the part `BC`. The internla energies at `B` and `C`, respectively, will be

View SolutionVariation of internal energy with density of `1 "mole"` of monatomic gas is depicted in Fig. Corresponding variation of pressure with voluem can be depicted as (assume the curve is rectangular hyperbola)
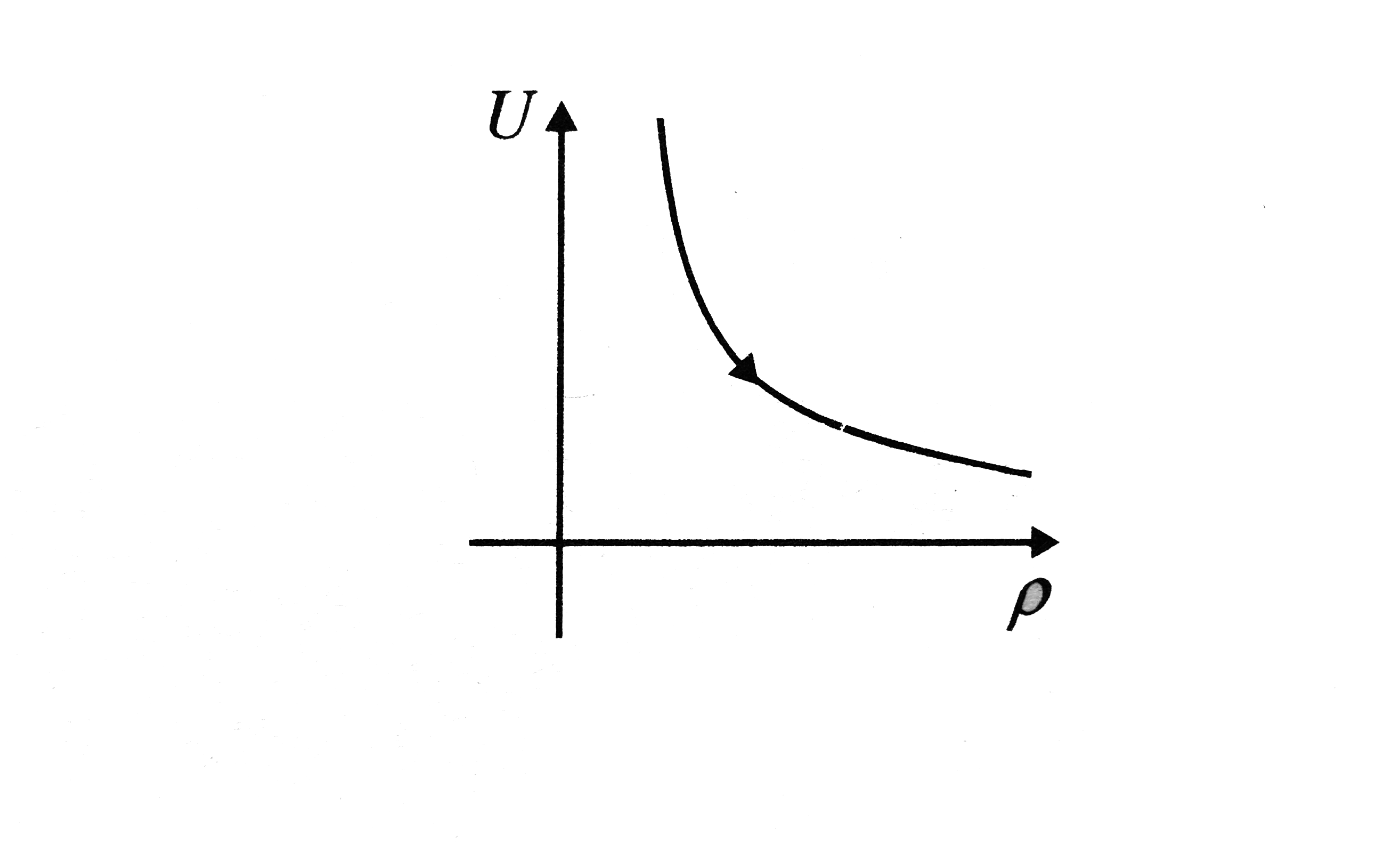
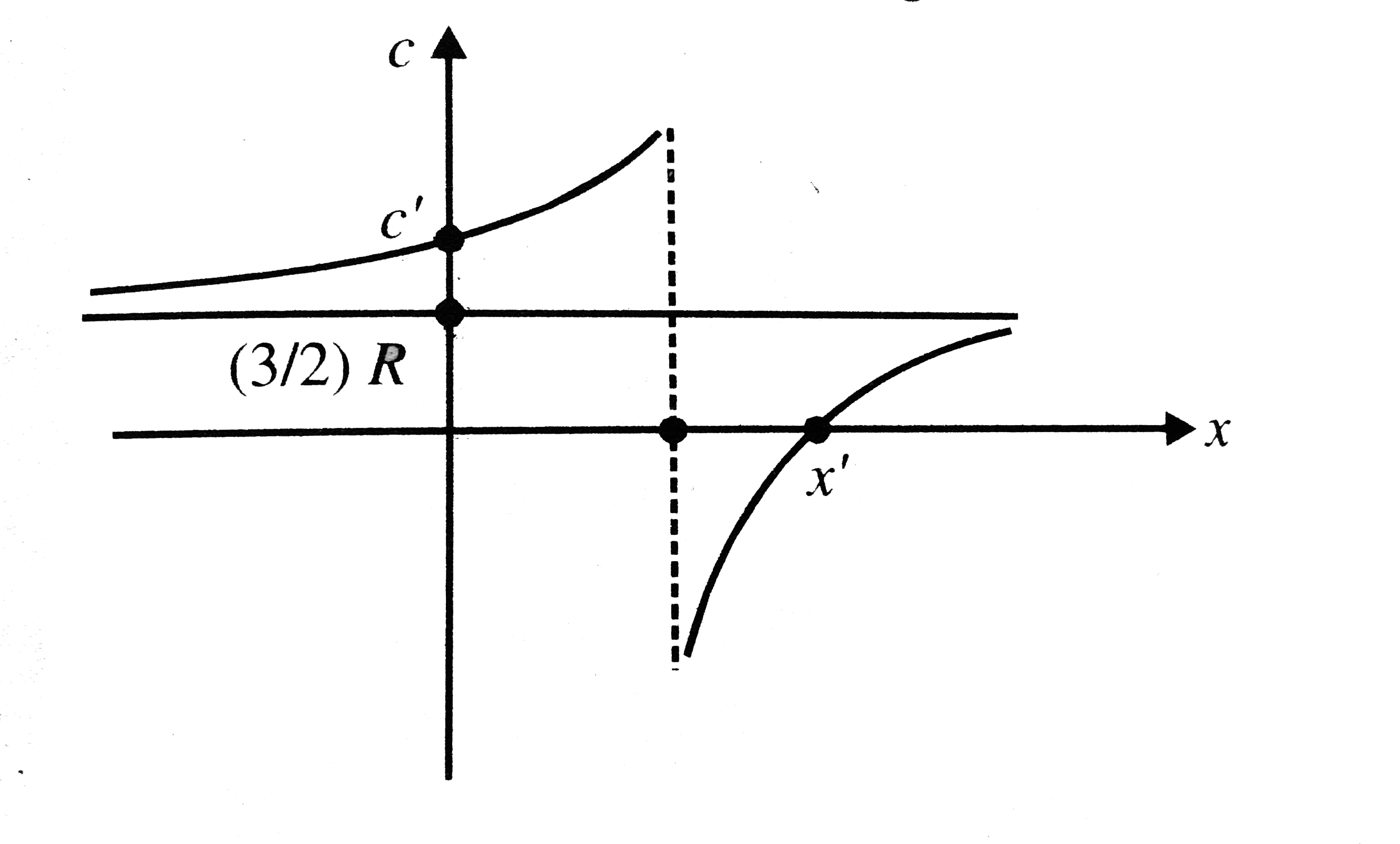
View SolutionOne mole of an ideal gas is taken along the process in which `PV' = ` constant. The graph shown represents the variation of molar heat capacity of such a gas with respect to `x`. The value of `c'` and `x'c` respectively, are given by
View SolutionA vessel of volume `20 L` contains a mixture o hydrogen and helium at temperature of `27^(@)C` and pressure `2.0 atm` The mass of the mixture is `5 g`. Assuming the gases to be ideal, the ratio of the mass of hydrogen to heat of helium in the given mixture will be
View SolutionA cylinder of ideal gas is closed by an 8kg movable piston of area `60cm^2`. The atmospheric pressure is 100kPa. When the gas is heated form `30^@C` to `100^@C`, the piston rises 20 cm. The piston is then fastened in the place and the gas is cooled back to `30^@C`. If `DeltaQ_1` is the heat added to the gas during heating and `DeltaQ_2` is the heat lost during cooling, find the difference.
View SolutionA certain ideal gas undergoes a polytropic process `PV^(n)` = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be `gamma`, then the range of values of `n` will be
View SolutionA cylindrical chamber `A` of uniform cross section is divided into two parts `X` and `Y` by a movalbe piston `P` which can slide without friction inside the chamber. Initially part `X` contains `1 "mol"` of a monochromatic gas and `Y` contains `2 mol` of a diatomic gas, and the volumes of `X` and `Y` are in the ratio `1:2` with both parts `X` and `Y` being at the same temperature `T`. Assuming the gases to be ideal, the work `W` that will be done in moving the piston slowly to the position where the ratio of the volumes of `X` and `Y` is `2:1` will be
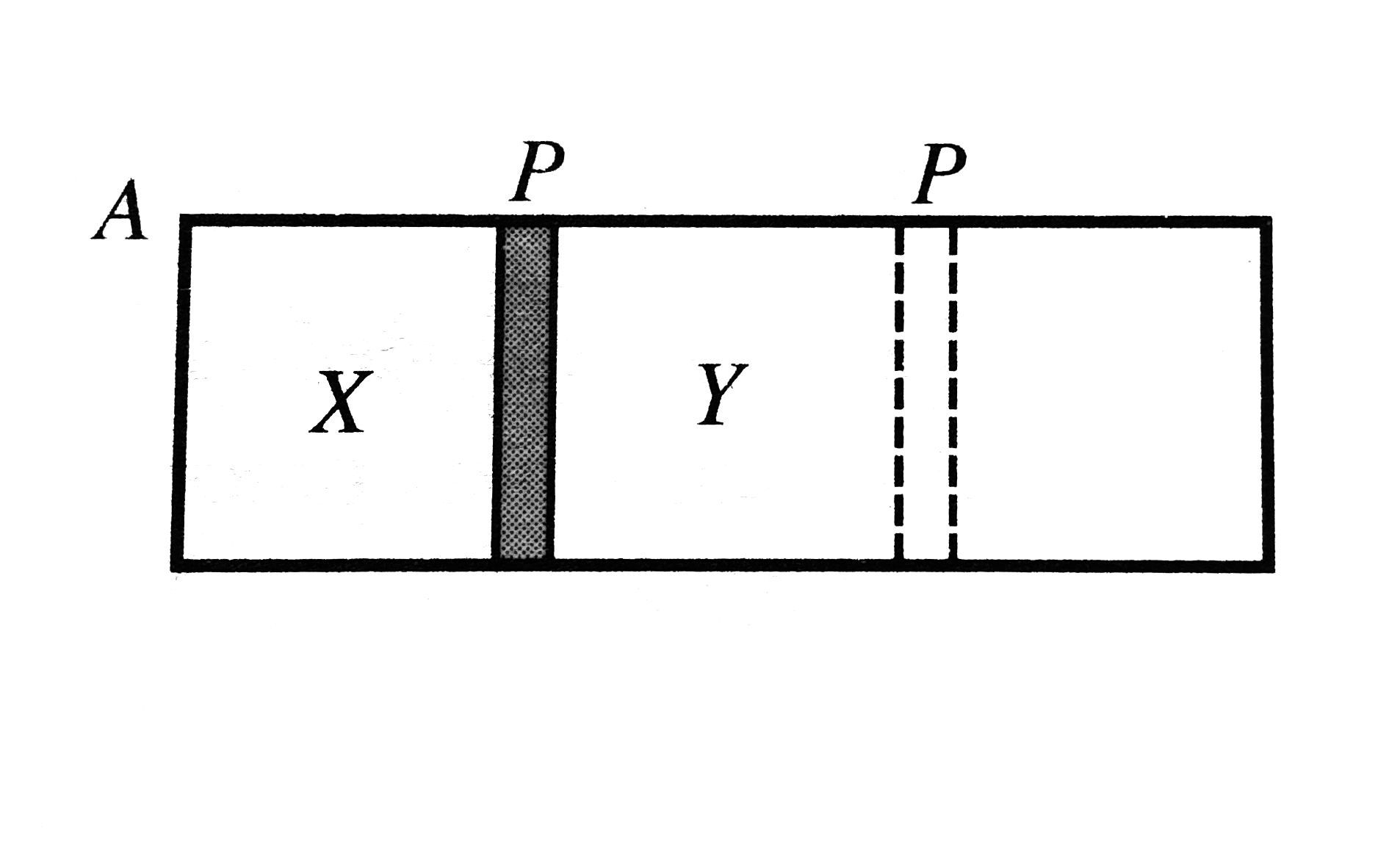
View SolutionAn ideal gas `(1` mol, monatomic) is in the intial state `P` (see Fig.) on an isothermal `A` at temperature `T_(0)`. It is brought under a constant volume `(2V_(0))` process to `Q` which lies on an adiabatic `B` intersecting the isothermal `A` at `(P_(0),V_(0),T_(0))`. The change in the internal energy of the gas during the process is (in terms of `T_(0)) (2^(2//3) = 1.587)`

View SolutionFigure shows an isochore, an isotherm, an adiabatic and two isobars of two gases on a work done versus heat supplied curve. The initial states of both gases are the same and the scales for the two axes are same.

View SolutionA stationary cylinder of oxygent used in a hospital has the following characteristics at room temperature `300 K`, gauge pressure `1.38 xx 10^(7)` Pa. volume `16 L`. If the flow area, measured at atmospheric pressure, is constant at `2.4 L//min`, the cylinder will last for nearly
View SolutionA sample of ideal gas is expanded to twice its original volume of `1.00m^3` in a quasi-static process for which `p=alphaV^2`, with `alpha=5.00 atm//m^6`, as shown in Fig. How much work is done by the expanding gas?
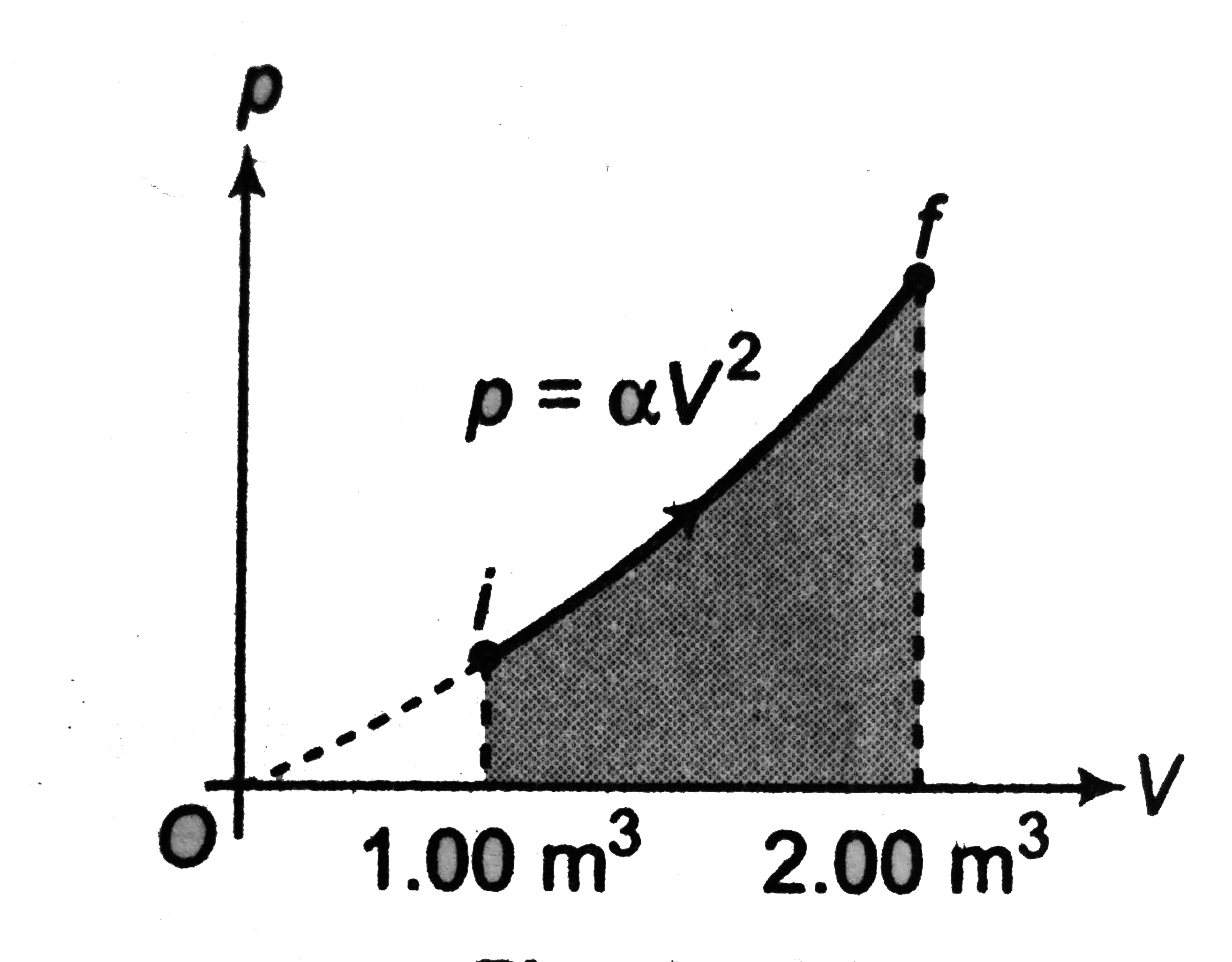
View SolutionOne mole of air `(C_(V) = 5R//2)` is confined at atmospheric pressure in a cylinder with a piston at `0^(@)C`. The initial volume occupied by gas is`V`. After the equivalent of `13200 J` of heat is transferred to it, the volume of gas `V` is nearly `(1 atm = 10^(5) N//m^(3))`
View SolutionA thermodynamic process is shown in Fig. The pressures and volumes corresponding to some points in the figure are
`P_(A) = 3 xx 10^(4) Pa` `V_(A) = 2 xx 10^(-3) m^(3)`
`P_(B) = 8 xx 10^(4) Pa` `V_(D) = 5 xx 10^(-3) m^(3)`
In the process `AB` `600 J` of heat is added to the system. The change in internal energy of the system in the process `AB` would be

View SolutionCarbon monoxide is carried around a closed cyclic processes `abc`, in which `bc` is an isothermal process, as shown in Fig. The gas absorbs `7000 J` of heat as its temperature is increased from `300 K` to `1000 K` in going from `a` to `b`. The quantity of heat ejected by the gas during the process `ca` is

View SolutionAn ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are `Q_1=5960J, Q_2=-5585J, Q_3=-2980J and Q_4=3645J`, respectively. The corresponding quantities of work involved are `W_1=2200J, W_2=-825J, W_3=-1100J and W_4` respectively.
(1) Find the value of `W_4`.
(2) What is the efficiency of the cycle
View SolutionPressure versus temperature graph of an ideal gas as shown in Fig.
Corresponding density `(rho)` versus volume `(V)` graph will be
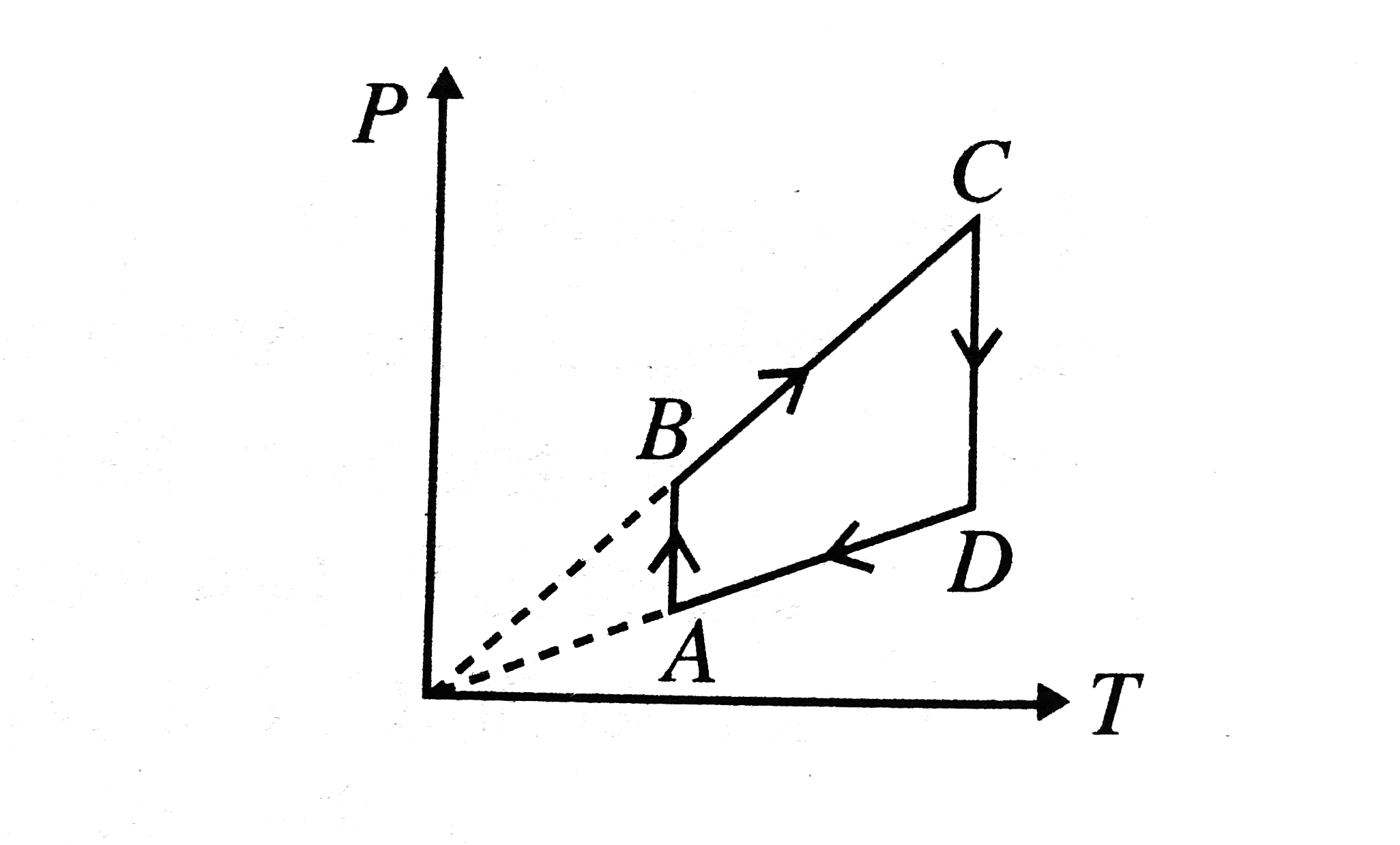
View SolutionAn ideal gas is taken through the cycle `AtoBtoCtoA,` as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
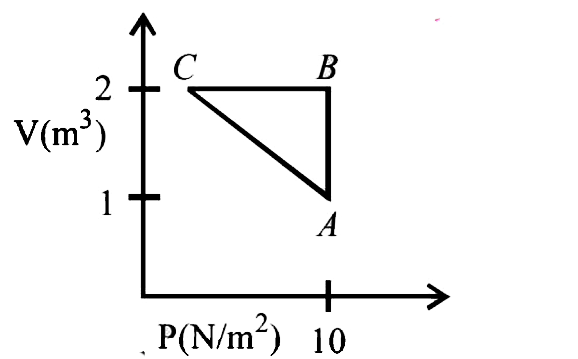
View SolutionTwo identical containers A and B with frictionless pistons contain the same ideal gas at the same temperature and the same velocity V. The mass of the gas in A is `m_A,` and that in B is `m_B`. The gas in each cylinder is now allowed to expand isothermally to the same final volume 2V. The changes in the pressure in A and B are found to be `DeltaP and 1.5 DeltaP` respectively. Then
View SolutionArgon gas is adiabatically compressed to half its volume. If `P, V` and `T` represent the pressure, volume and temperature of the gasous, respectively, at any stage, then the correct equation representing the process is
View SolutionA fixed mass of helium gas is made to undergo a process in which its pressure varies linearly from `1 kPa` to `2 kPa`, in relation to its volume as the latter varies from `0.2 m^(3)` to `0.4 m^(3)`. The heat absorbed by the gas will be
View SolutionOxygen gas is made to undergo a process in which its molar heat capacity `C` depends on its absolute temperature `T` as `C = alpha T`. Work done by it when heated from an initial temperature `T_(0)` to a final temperature `2 T_(0)`, will be
View SolutionIf the ratio of specific heat of a gas of constant pressure to that at constant volume is `gamma`, the change in internal energy of the mass of gas, when the volume changes from `V` to `2V` at constant pressure `p` is
View SolutionA gas is at 1 atm pressure with a volume `800 cm^(3)`. When `100 J` of heat is supplied to the gas, it expands to `1L` at constant pressure. The change in its internal energy is
View SolutionA fixed mass of a gas is first heated isobarically to double the volume and then cooled isochorically
View SolutionAn ideal heat engine has an efficiency `eta`. The cofficient of performance of the engine when driven backward will be
View SolutionTwo moles of helium gas are taken along the path `ABCD` (as shown in Fig.) The work done by the gas is

View SolutionFigure shows the adiabatic curve for `n` moles of an ideal gas, the bulk modulus for the gas corresponding to the point `P` will be

View SolutionTwo moles of an ideal gas is contained in a cylinder fitted with a frictionless movalbe piston, exposed to the atmosphere, at an initial temperature `T_(0)`. The gas is slowly heated so that its volume becomes fout times the initial value. The wor done by gas is
View SolutionThe equation of state for a gas is given by `PV = eta RT + alpha V`, where `eta` is the number of moles and `alpha` a positive constant. The intinal pressure and temperature of 1 mol of the gas contained in a cylinder is `P_(0)` and `T_(0)`, respectively. The work done by the gas when its temperature doubles isobarically will be
View SolutionA sound wave passing volume `1 m^(3)` is divided into two equal compartments by a partition. One of these compartments contains an ideal gas at `300 K`. The other compartment is vacuum. The whole system is thermally isolated from its surroundings. The partition is removed and the gas expands to occupy the whole volume of the container. Its temperature now would be
View SolutionA container of volume `1m^3` is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View SolutionThe molar specific heat of oxygen at constant pressure `C_(P) = 7.03 cal//mol .^(@)C` and `R = 8.31 J//mol .^(@)C`. The amount of heat taken by 5 mol of oxygen when heated at constant volume from `10^(@)C` to `20^(@)C` will be approximately.
View SolutionFour moles of hydrogen, 2 moles of helium and 1 mole of water form an ideal gas mixture. What is the molar specific heat at constant pressure of mixture ?
View SolutionIn a adiabatic process is increased by `2//3%` if `C_(P)//C_(V) = 3//2`. Then the volume decreases by about
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionCarbon monoxide is carried around a closed cyclic processes `abc`, in which `bc` is an isothermal process, as shown in Fig. The gas absorbs `7000 J` of heat as its temperature is increased from `300 K` to `1000 K` in going from `a` to `b`. The quantity of heat ejected by the gas during the process `ca` is

View SolutionIf for hydrogen `C_(P) - C_(V) = m` and for nitrogen `C_(P) - C_(V) = n`, where `C_(P)` and `C_(V)` refer to specific heats per unit mass respectively at constant pressure and constant volume, the relation between `m` and `n` is (molecular weight of hydrogen = 2 and molecular weight or nitrogen = 14)
View SolutionFive moles of hydrogen `(gamma = 7//5)`, initially at `STP`, is compressed adiabatically so that its temperature becomes `400^(@)C`. The increase in the internal energy of the gas in kilojules is `(R = 8.30 J//mol-K)`
View SolutionOne mole of gas having `gamma = 7//5` is mixed with 1 mole of a gas having `gamma = 4//3`. What will be `gamma` for the mixture ?
View SolutionThe specific heats of argon at constant pressure and constant volume are `525 J//kg` and `315 J//kg`, respectively. Its density at `NTP` will be\
View SolutionAn ideal gas expands isothermally from volume `V_(1)` to `V_(2)` and is then compressed to original volume `V_(1)` adiabatically. Initialy pressure is `P_(1)` and final pressure is `P_(3)`. The total work done is `W`. Then
View SolutionInternal energy of `n_(1)` mol of hydrogen of temperature `T` is equal to the internal energy of `n_(2)` mol of helium at temperature `2T`. The ratio `n_(1) // n_(2)` is
View SolutionAn ideal gas `(gamma = 1.5)` is expanded adiabatically. How many times has the gas to be expanded to reduce the roo-mean-square velocity of molecules becomes half ?
View Solution
Single Correct questions and complete solutions for chapter KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS of CENGAGE PHYSICS (HINGLISH) of Class 11