Complete Solutions to Illustration of chapter KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
The mass of hydrogen molecule is `3.23 xx 10^(23)` hydrogen molecules strike `2 cm^(2)` of a wall per second at an angle of `45^(@)` with the normal when moving with a speed of `10^(5) cm s^(-1)`, what pressure do they exert on the wall ? Assume collision to be elasitc.
View SolutionA parallel beam of nitrogen molecules moving with velocity `v = 400 m s^(-1)` imprings on a wall at an angle `theta = 30^(@)` to its normal. The concentration of molecules in the beam is `n = 9 xx 10^(18) cm^(-3)`. Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.
View Solution(a) Calculate (i) root-mean-square speed and (ii) the mean energy of 1 mol of hyderogen at STP given that density of hydrogen is `0.09 kg//m^(3)`. (b) Given that the mass of a molecule of hydergen is `3.34 xx 10^(-27)` kg, calculate Avogadro's number. (c ) Calculate Boltmann's constant.
View SolutionGiven molecular weight of hydrogen molecule is `M = 2.016 xx 10^(-3) kg//mol`. Calculate the root-mean-square speed of hydrogen molecules `(H_(2))` at `373.15 K (100^(@) C)`.
View SolutionOne mole of oxygen occupies a volume of 24 L at `20^(@) C` and 1 atm pressure. What is the rms speed of an oxygen? Find the total translational kinetic energy and the total momentum of the molecules.
View SolutionOne gram mole of oxygen at `27^@` and one atmospheric pressure is enclosed in vessel.
(i) Assuming the molecules to be moving the `V_(rms)`, Find the number of collisions per second which the molecules make with one square metre area of the vessel wall.
(ii) The vessel is next thermally insulated and moved with a constant speed `V_0`. It is then suddenly stopped. The process results in a rise of the temperature of the gas by `1^@C`. Calculate the speed `V_0`.
View SolutionA glass bulb of volume `400 cm^(3)` is connected to another bulb of volume `200 cm^(3)` by means of a tube of negligible volume. The bulbs contain dry air and are both at a common temperature and pressure of `20^(@) C` and 1.000 atm, respectively. The larger bulb is immersed in steam at `100^(@) C` and the smaller in melting ice at `0^(@)`. Find the final common pressure.
View SolutionExplain whether (a) `T_(2) gt T_(1)`, (b) `P_(2) gt P_(1)` and (c ) `V_(2) gt V_(1)` or otherwise in Fig., which represent in isothermal, isobaric, and isochoric processes for the same mass of an ideal gas, respedtively.

View SolutionThe three diagrams below depict three different processes for a given mass of an ideal gas. What information can be drawn regarding the change of (a) pressure, (b) volume and (c ) temperature of the gas from the plots as shown in Fig., respectively.

View SolutionDraw the P-T and V-T diagrams of an isochoric process of n moles an ideal gas from pressure `P_(0)` volume `V_(0)` to pressure `4P_(0)`, indicating the pressures and temperatures of the gas in the initial and the final states.
View SolutionDraw the P-T and V-T diagrams for an isobaric process of expansion, corresponding to n moles of an ideal gas at pressure `P_(0)` from `V_(0)` to `2 V_(0)`
View SolutionA Cycle process ABCA shown in V-T diagram Fig. is preformed with a constant mass of an ideal gas. Show the same process on a P-V diagram.
View SolutionCalculate (a) the average kinetic energy of translation of an oxygen molecule at `27^(@) C` (b) the total kinetic energy of an oxygen molecule at `27^(@)C` (c ) the total kinetic energy in joule of one mole of oxygen at `27^(@)`. Given Avogadro's number `= 6.02 xx 10^(23)` and Boltzmann's constant `= 1.38 xx 10^(-23) J//(mol-K)`.
View SolutionA light container having a diatomic gas enclosed with in is moving with velocity v. Mass of the gas is M and number of moles is n,
a. What is the kinetic energy of gas w.r.t. centre of mass of the system ?
b. What is K.E. of gas w.r.t. ground ?
View SolutionTwo monconducting containers having volume `V_(1)` and `V_(2)` contain monoatomic and dimatomic gases respectivley. They are connected as shown in figure. Pressure and temperature in the two containers are `P_(1), T_(1)` and `P_(2), T_(2)` respectively. Initially stop cock is closed, if the stop coc is opened find the final pressure and temperature.
View SolutionAn ideal gas has a specific heat at constant pressure `C_P=(5R)/2`. The gas is kept in a closed vessel of volume `0.0083m^3`, at a temperature of 300K and a pressure of `1.6xx10^6 N//m^2`. An amount of `2.49xx10^4` Joules of heat energy is supplied to the gas. Calculate the final temperature and pressure of the gas.
View SolutionA vessel of volume `0.2 m^(3)` contains hydrogen gas at temperature 300 K and pressure 1 bar. Find the heat required to raise the temperature to 400 K. The molar heat capacity of hydrogen at constant volume is `5 cal//mol K`.
View SolutionAbout 0.014 kg nitrogen is enclosed in a vessel at temperature of `27^(@)C` How much heat has to be transferred to the gas to double the rms speed of its molecules ? `(R = 2 cal//mol K)`
View SolutionA gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with `gamma=(5/3)` and some amount of gas B with `gamma=7/5` at a temperature T.
The gases A and B do not react with each other and are assumed to be ideal. Find the number of gram moles of the gas B if `gamma` for the gaseous mixture is `(19/13)`.
View SolutionHow much heat energy should be added to the gaseous mixture consisting of 1 g of hydrogen and 1g of helium to raise it s temperature from `0^(@)C` to `100^(@)C`
(a) at constant volume,
b. at constant pressure `(R = 2 cal//mol K)`?
View SolutionCalculate the specific heat capacity `C_(r)` of a gaseous mixture consisting of `v_(1)` moles of a gas of adiabatic exponent `gamma_(1)` and `v_(2)` moles of another gas of adiaqbatic exponent `gamma_(2)`.
View SolutionA vessel of volume `2 xx 10^(-2) m^(3)` contains a mixture of hydrogen at `47^(@)C` temperature and `4.15 xx 10^(5) N//m^(2)` Pressure. The mass of the mixture is `10^(-2) kg`. Calculate the masses of hydrogen and helium in the given mixture.
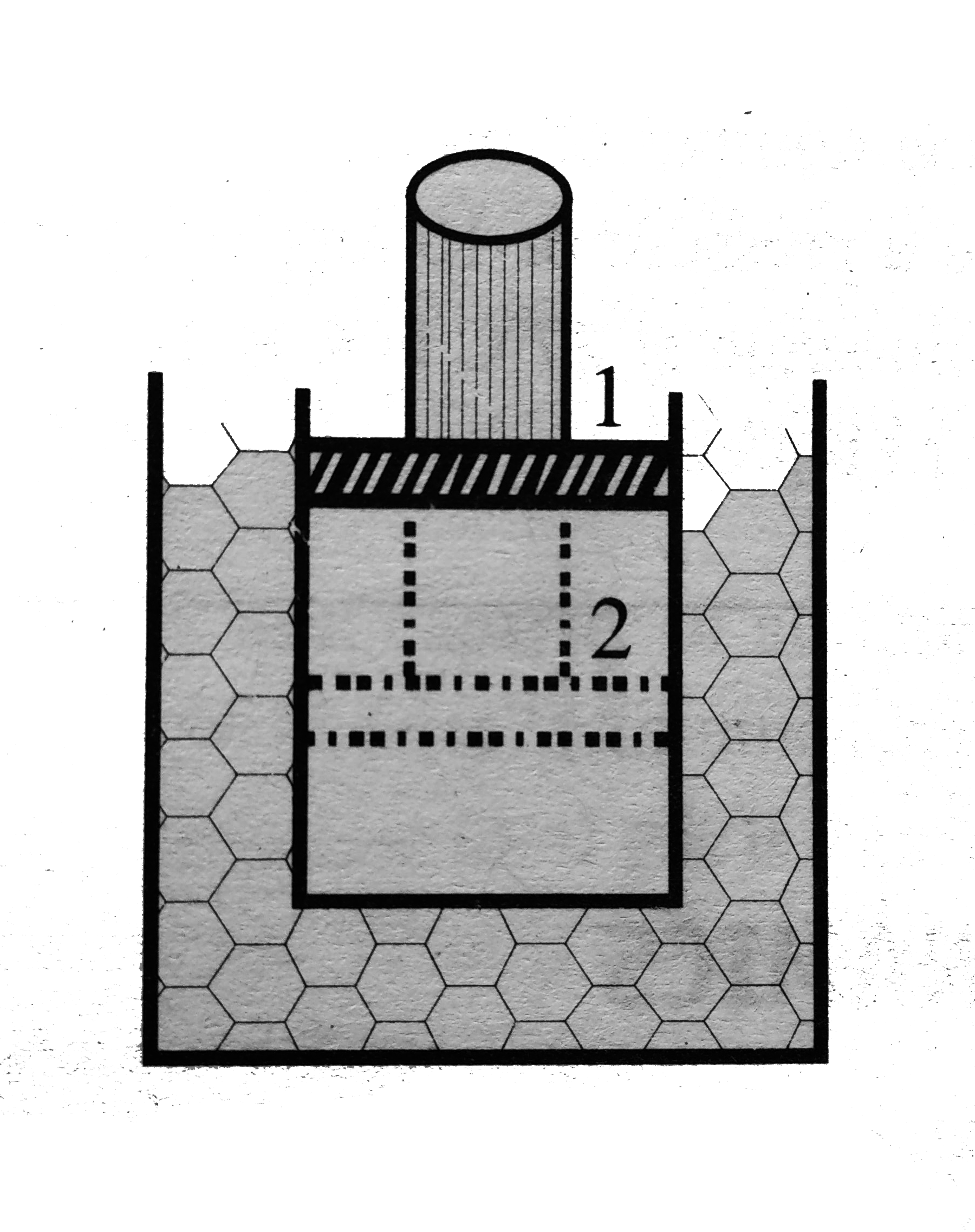
View SolutionFigure shows a cylinder closed by a movable piston containing an ideal gas. The piston is quickly pushed down from position 2. The piston is held at position 2 until the gas is again at `0^(@)C` and then is slowly raised back to position 1. If 100 g of ice melts during the cycle, how much work is done on the gas?
View SolutionA quantity of gas occupies an initial volume `V_(0)` at pressure `p_(0)` and temperature `T_(0)`. It expands to a volume V (a) constant temperature and (b) constant pressure. In which case does the gas do more work ?

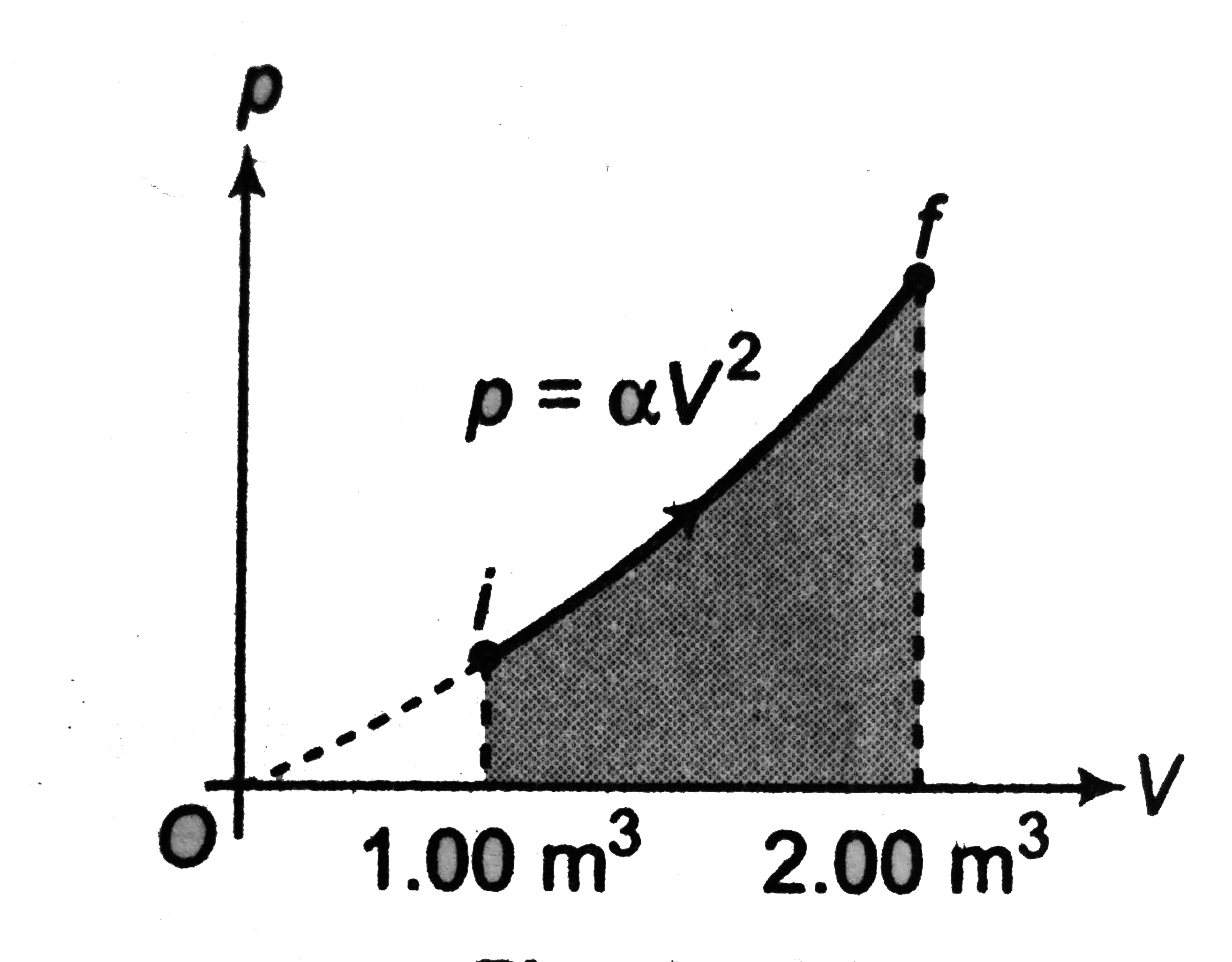
View SolutionA sample of ideal gas is expanded to twice its original volume of `1.00m^3` in a quasi-static process for which `p=alphaV^2`, with `alpha=5.00 atm//m^6`, as shown in Fig. How much work is done by the expanding gas?
View SolutionDetermine the work done by an ideal gas doing `1 rarr 4 rarr 3rarr 2 rarr 1`.
Given `P_(1) = 10^(5) Pa, P_(0) = 3 xx 10^(5) Pa, P_(3) = 4 xx 10^(5) Pa` and `V_(2) - V_(1) = 10 L`.

View SolutionAn ideal gas is enclosed in a cylinder with a movable piston on top of it. The piston has a mass of 800 g and an area of `5.00 cm^(2)` and is free slide up and down, keeping the pressure of the gas constant. How much work is done on the gas as the temperature of 0.200 mol of the gas is raised from `20.0^(@)C` to `300^(@)C` ?
View SolutionThe cylinder shown in the figure has conducting walls and temperature of the surrounding is T, the pistonj is initially in equilibrium, the cylinder contains n moles of a gas, Now the piston is displaced slowly by an external agent to make the volume double of the initial. Find work done by external agent in term of n, R, T

View SolutionA non conducting piston of mass m and area of cross section A is placed on a non conducting cylinder as shown in figure. Temperature, spring constant, height of the piston are given by T,K,h respectively. Initially spring is relaxed and piston is at rest. Find
(a) Number of moles
(b) Work done by gas to displaced the piston by distance d when the gas is heated slowly.
(c ) Find the final temperature

View SolutionWhen a thermodynamic system is taken from an initial state I to a final state F along the path IAF, as shown in Fig. the heat energy absorbed by the system is `Q = 55 J` and work done by the system is `W = 25 J`. If the same system is taken along the path IBF, the value of `Q = 35 J`.
(a) If `W = - 15 J` for the curved path FI, how much heat energy is lost by the system along this path ?
(b) If `U_(1) = 10 J`, what is `U_(F)` ?
(d) If `U_(B) = 20 J`, what is Q for the process BF and IB ?
View SolutionHow much work is done on the steam when 1.00 mol of water at `100^(@)C` boils and becomes 1.00 mole of steam at `100^(@)C` at 1.00 atm pressure? Assume the steam to behave as an ideal gas , detemine the change in the internal energy of the material as it vapourizes.
View SolutionAn ideal gas initially at 30 K undergoes an isobaric expansion at 2.50 k Pa. If the volume increases from `1.00 m^(2)` to `3.00 m^(3)` and 12.5 kJ is transferred to the gas by heat, what are (a) the change in its internal energy and (b) its final temperature ?
View SolutionThe temperature of 3 kg of nitrogen is raised form `10^(@)C` to `100^(@)C`, Compute the heat added, the work done, and the change in internal energy if (a) this is done at constant volume and (b) if the heating is at constant pressure. For nitrogen
`C_(p) = 1400 J kg^(-1) K^(-1)` and `C_(v) = 740 J kg^(-1) K^(-1)`.
View SolutionGaseous hydrogen contained initially under standard conditions in sealed vessel of volume `V = 5 L` was cooled by `Delta T = 55 K`. Find how much the internal energy of the gas will change and what amount of heat will be lost by the gas.
View SolutionThe volume of a monatomic ideal gas increases linearly with pressure, as shown in Fig. Calculate (a) increase in internal energy, (b) work done by the gas and (c ) heat supplied to the gas.

View SolutionA Vessel contains helium, which expands at constant pressure when 15 kJ of heat is supplied to it. What will be the variation of the internal energy of the gas? What is the work performed in the expansion?
View SolutionThe volume of one mode of an ideal gas with adiabatic exponent `gamma` is varied according to the law `V = a//T`, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by `Delta T`.
View SolutionA 2.00 mol sample of helium gas initially at 300 K and 0.400 atm is compressed isothermally to 1.20 atm. Noting that the helium behaves as an ideal gas, find (a) the final volume of the gas, (b) the work done on the gas and (c ) the energy transferred by heat.
View SolutionAs a result of the isobaric heating by `DeltaT=72K`, one mole of a certain ideal gas obtain an amount of heat `Q=1.6kJ`. Find the work performed by the gas, the increment of its internal energy and `gamma`.
View SolutionSix grams of hydrogen gas at a temperature of 273 K isothoermally expanded to five times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. Find the total amount of heat absorbed by the gas during the entire process.
View SolutionTwo moles of an ideal gas at temperature `T_(0) = 300 K` was cooled isochorically so that the pressure was reduced to half. Then, in an isobaric process, the gas expanded till its temperature got back to the initial value. Find the total amount of heat absorbed by the gas in the processs
View SolutionT-V curve of cyclic process is shown below, number of moles of the gas are n find the total work done during the cycle.

View SolutionP-T curve of a cyclic process is shown. Find out the works done by the gas in the given proces if number of moles of the gas are n.

View SolutionIn a cylinder, 2.0 moles of an ideal monatomic gas initially at `1.0 xx 10^(6)` Pa and 300 K expands until its volume doulbles. Compute the work done if the expansion is (a) isothermal, (b) adiabatic and (c ) isobaric.
View SolutionOne mole of a perfect gas, initally at a pressure and temperature of `10^(5) N//m^(2)` and 300 K, respectively, expands isothermally unitl its volume is doubled and then adiabatically until its volume is again doubled. Find final pressure and temperature of the gas Find the total work done during the isothermal and adiabatic processes. Given `gamma = 1.4`. Also draw the P-V diagram for the process.

View SolutionAn ideal gas `(C_p / C_v = gamma)` is taken through a process in which the pressure and volume vary as `(p = aV^(b))`. Find the value of b for which the specific heat capacity in the process is zero.
View SolutionA cylindrical container having non-conducting walls is partitioned in two equal parts such that the volume of the each parts is eqaul to `V_(0)` A movable non-conducting piston is kept between the two parts. Gas on left is slowly heated so that the gas on right is compressed upto volume `V_(0)//8`. Find pressure and temperature on both sides if initial pressure and temperature, were `P_(0)` and `T_(0)` respectively. Also find heat given by the heater to the gas (number of moles in each parts is n)

View SolutionA reversible heat engine carries 1 mole of an ideal monatomic gas aroung the cycle 1-2-3-1. Process 1-2 takes place at constant volume, process 2-3 take place at constant volume, process 2-3 is adiabatic, and process 3-1 takes place at constant pressure. Complete the values for the heat `Delta Q`, the change in internal energy `Delta U`, and the work done `Delta `, for each of the three processes and for the cycle as a whole.

View SolutionConsider the cyclic process `ABCA` on a sample of `2.0 mol` of an ideal gas as shown in the figure. Temperature of the gas at `A` and `B` are `300 K` and `500 K` respectively. A total of `1200 J` heat is withdrawn from the sample in the process. Find the work done by the gas in part `BC`. take `R=8.3 JK^(-1) mol^(-1)`

View SolutionA sample of an ideal gas has pressure `p_(0)`, volume `V_(0)` and tempreture `T_(0)`. It is isothermally expanded to twice its original volume.It is then compressed at constant pressure to have the original volume `V_(0)`. Finally, the gas is heated at constant volume to get the original temperature.
(a) Show the process in a V-T diagram
(b) Calculate the heat absorbed in the process.
View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionThree moles of an ideal gas `(C_p=7/2R)` at pressure, `P_A` and temperature `T_A` is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure `P_A`.
(a) Sketch P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
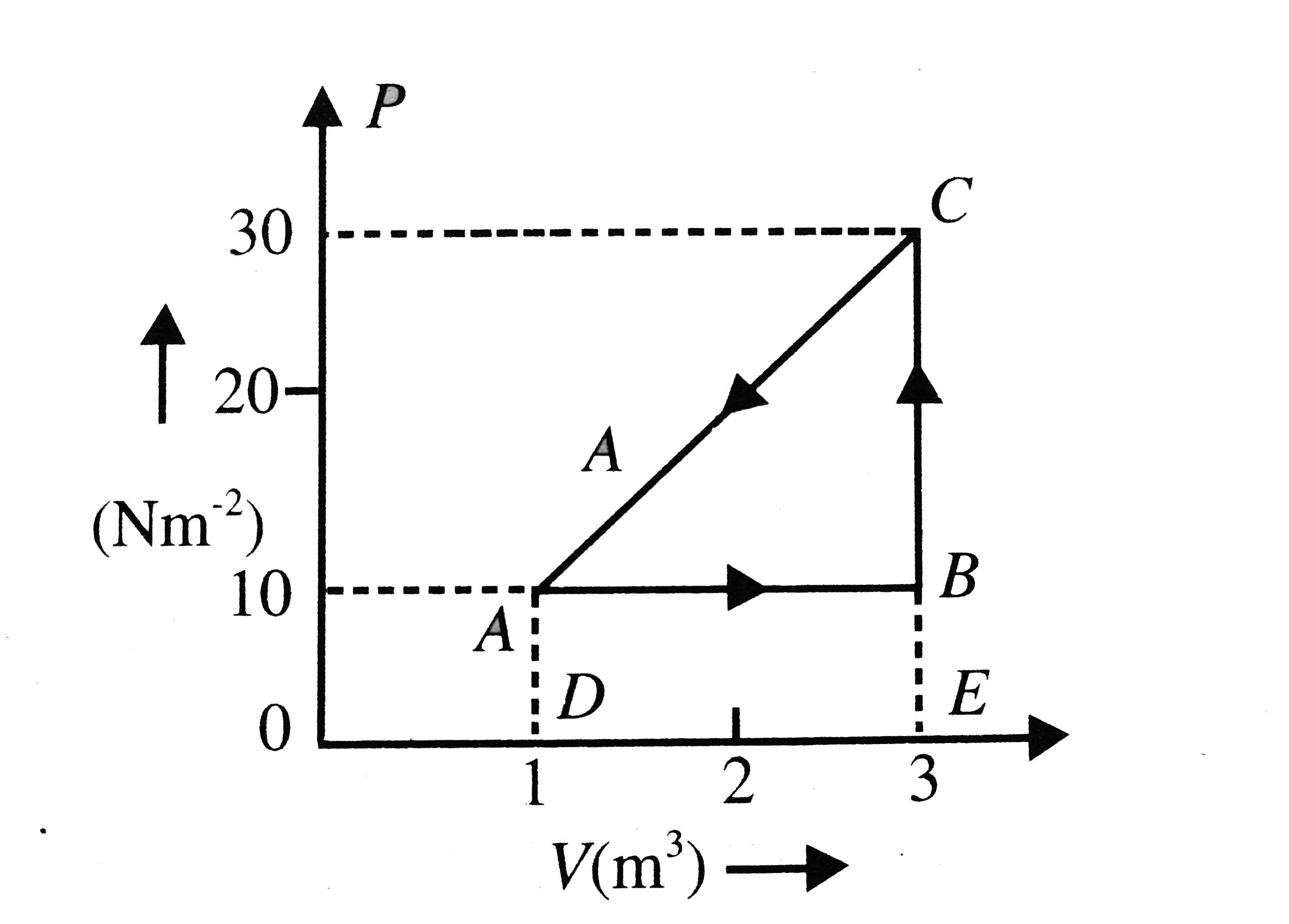
View SolutionAn ideal gas is taken round a cyclci thermodynamic process ABCA as shown if Fig. If the internal energy of the gas at point A is assumed zero while at B it is 50 J. The heat absorbed by the gas in the process BC is 90 J.
(a) What is the internal energy og the gas at point C ?
(b) How much heat energy is absorbed by the gas in the process AB?
(c ) Find the heat energy rejected or absorbed by the gas in the process CA.
(d) What is the net work done by the gas in the complete cycle ABCA ?
View SolutionA fixed mass of oxygen gas performs a cyclic process ABCA as shown. Find the efficiency of the process.

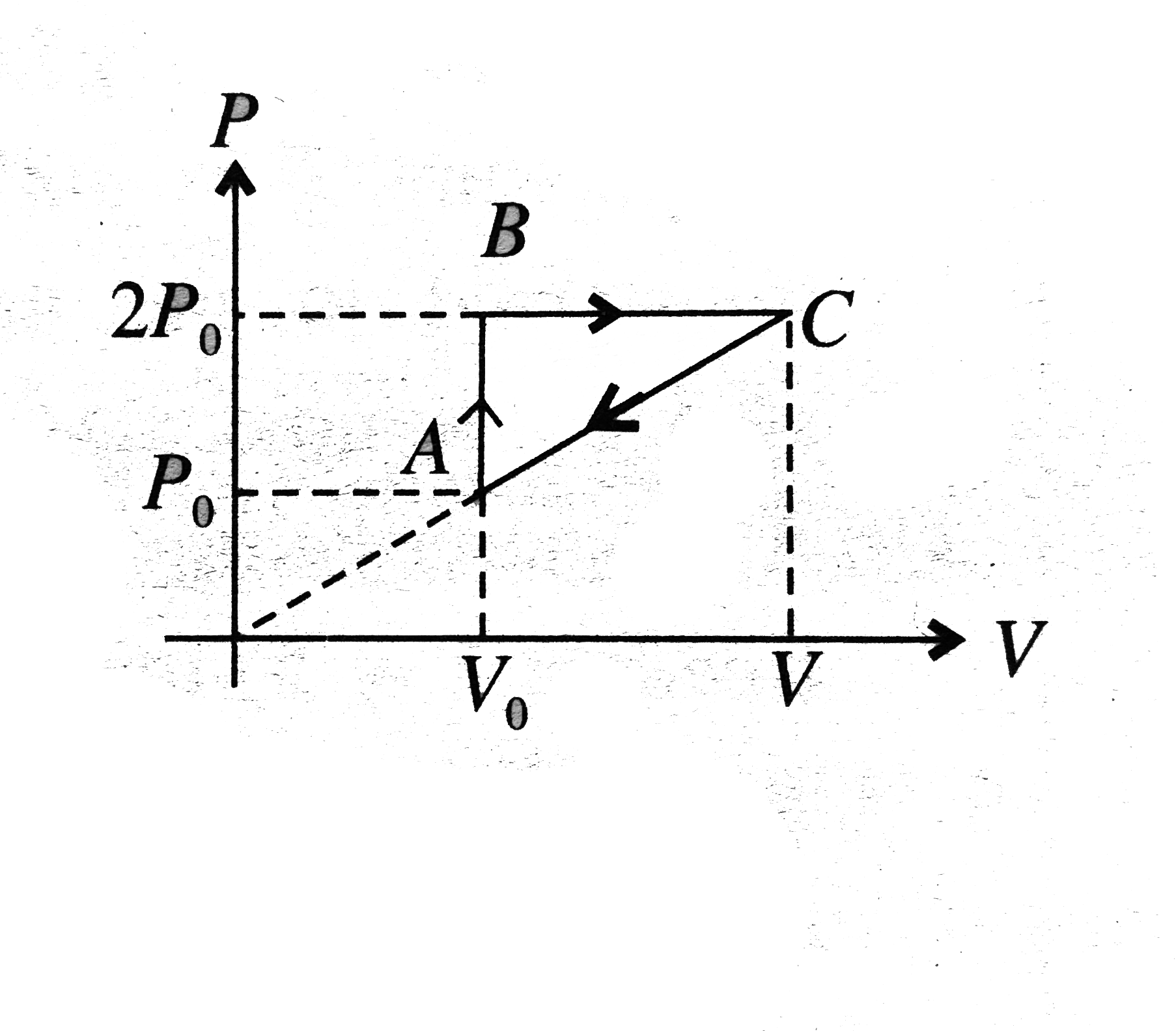
View Solutionn moles of a diatomic gas has undergone a cyclic process ABC as shown in figure. Temperature at a is `T_(0)`. Find
a. Volume at C ?
b. Maximum temperature ?
c. Total heat given to gas ?
d. Is heat rejected by the gas, if yes how much heat is rejected ?
e. Find out the efficiency
View Solution
Illustration questions and complete solutions for chapter KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS of CENGAGE PHYSICS (HINGLISH) of Class 11