Complete Solutions to Linked Comperhension of chapter NEWTON'S LAWS OF MOTION 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 1 |
| CENGAGE PHYSICS | Linked Comperhension |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
In the system shown in fig. `m_(1) gt m_(2)` . The system is held at rest by thread BC. Now thread BC is burnt. Answer the following:

Before burnig the thread, what are the tensions in spring and thread BC, respectively?
View SolutionIn the system shown in fig. `m_(1) gt m_(2)` . The system is held at rest by thread BC. Now thread BC is burnt. Answer the following:
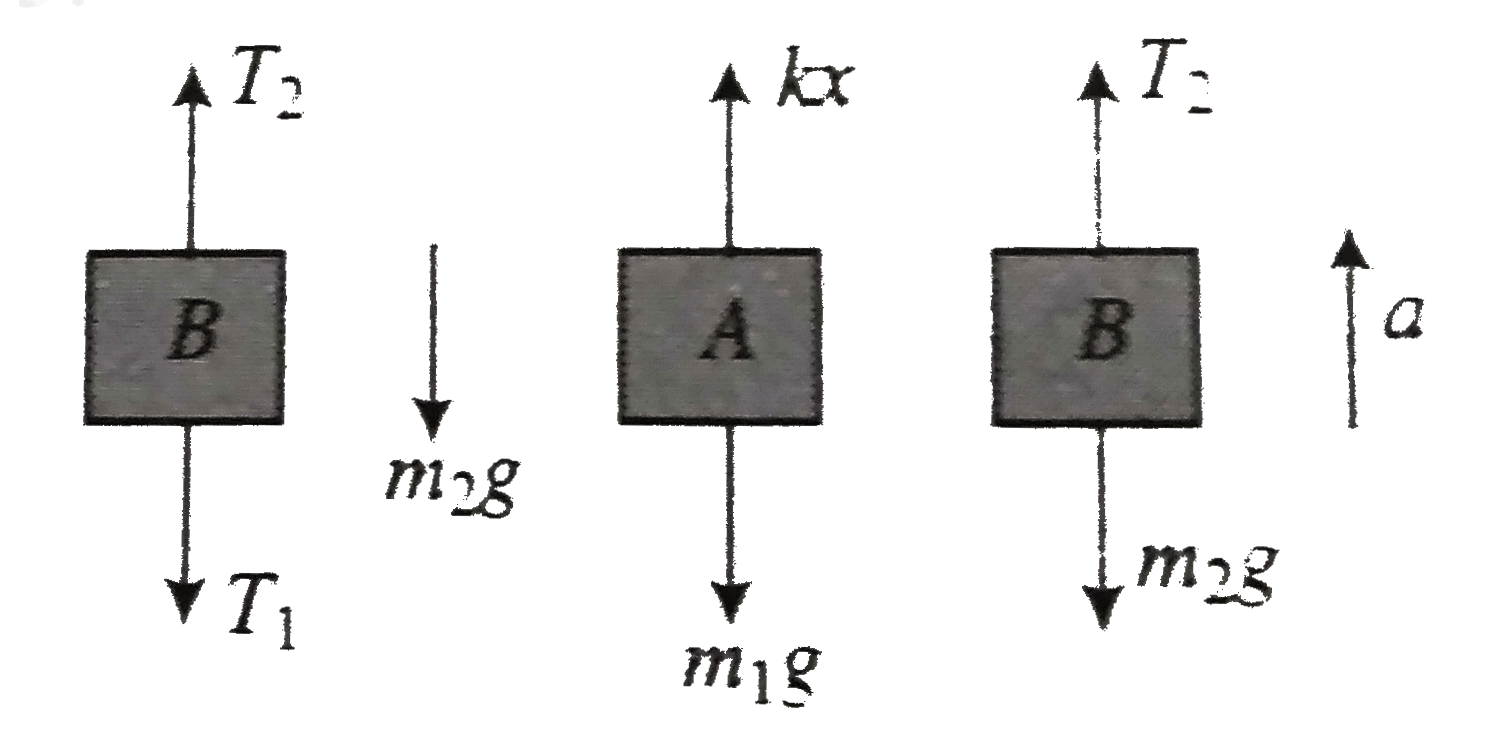
Just after burning the thread, what is the tension in the spring?
View SolutionIn the system shown in fig. `m_(1) gt m_(2)` . The system is held at rest by thread BC. Now thread BC is burnt. Answer the following:
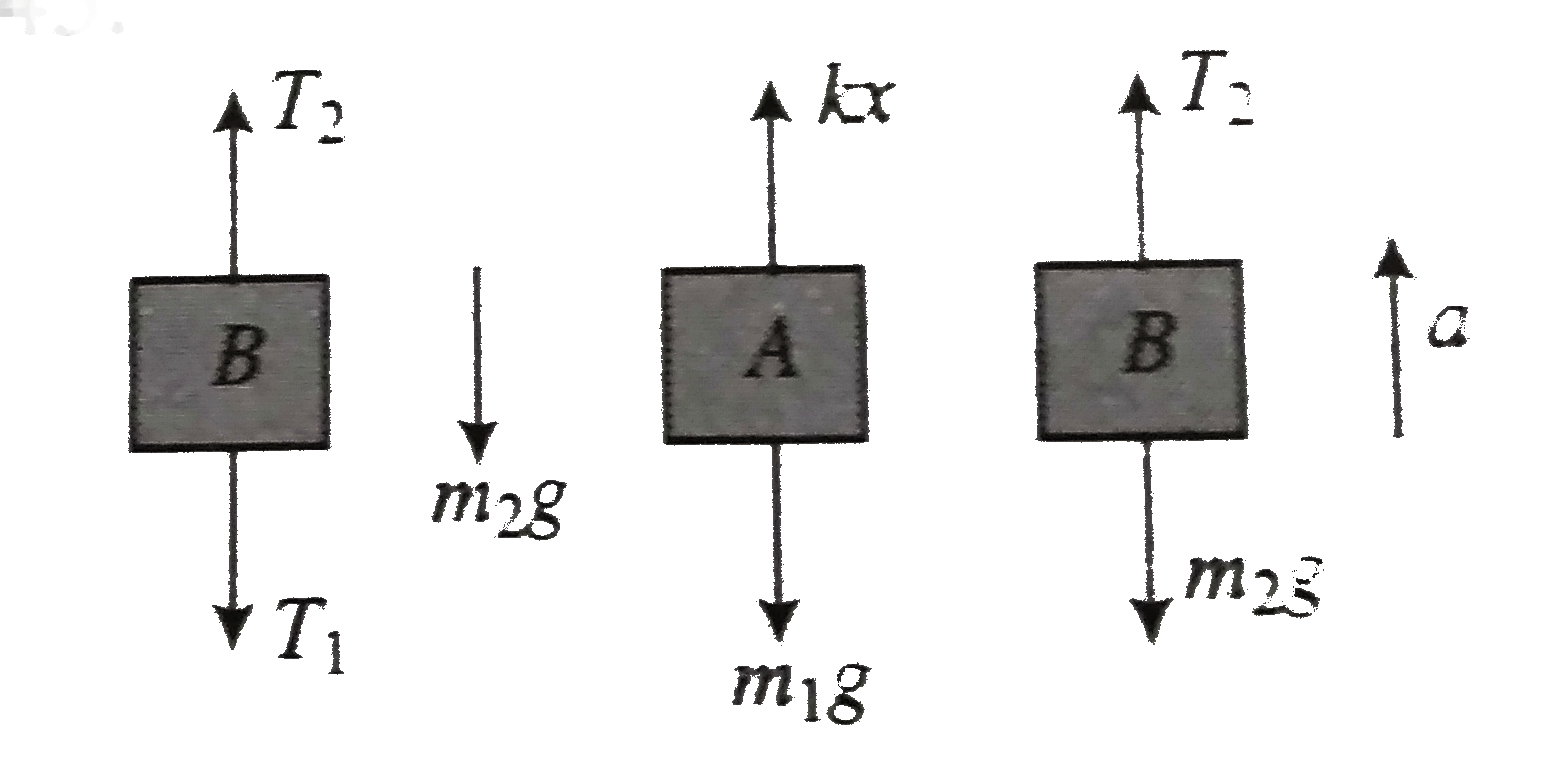
Just after burning the thread, what is the acceleration of `m_(2)`?
View SolutionTwo block `A` and `B` of masses `1kg` and`2kg` respectively are connected by a string, passing over a light frictionless pulley as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment `t = 0`, a force `F = 20 t` starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velocity of `A` when `B` loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =`g =10 m//s^(2))`
View SolutionTwo block `A` and `B` of masses `1kg` and`2kg` respectively are connected by a string, passing over a light frictionless pulley as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment `t = 0`, a force `F = 20 t` starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velocity of `A` when `B` loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =`g =10 m//s^(2))`
View SolutionTwo block `A` and `B` of masses `1kg` and`2kg` respectively are connected by a string, passing over a light frictionless pulley as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment `t = 0`, a force `F = 20 t` starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velocity of `A` when `B` loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =`g =10 m//s^(2))`
View SolutionA ball of mass 0.2 kg travelling in a straight line with a speed of `m//s` along negative x- axis id deflected by a bat `15 m//s` along negative x - axis is deflected by a bat at an angle of `30^(@)` If the speed of the ball after deflection is `10 m//s`, find the impulse on the ball.
View SolutionA ball of mass 0.2 kg travelling in a straight line with a speed of `m//s` along negative x- axis id deflected by a bat `15 m//s` along negative x - axis is deflected by a bat at an angle of `30^(@)` If the speed of the ball after deflection is `10 m//s`, find the impulse on the ball.
View SolutionA ball weighing `10g` hits a hard surface vertically with a speed of `5m//s` and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for `0.01s` The average force exerted by the surface on the ball is .
View SolutionIn the system shown in fig., `m_(A)=4m`, `m_(B)=3m`, and `m_(c)=8m`. Friction is absent everywhere. String is inextensible and light. If the system is released from rest, then

Acceleration of Block B is
View SolutionIn the system shown in fig., `m_(A)=4m`, `m_(B)=3m`, and `m_(c)=8m`. Friction is absent everywhere. String is inextensible and light. If the system is released from rest, then

Acceleration of block C is
View SolutionIn the system shown in fig., `m_(A)=4m`, `m_(B)=3m`, and `m_(c)=8m`. Friction is absent everywhere. String is inextensible and light. If the system is released from rest, then

Acceleration of Block B is
View SolutionIn the system shown in fig., `m_(A)=4m`, `m_(B)=3m`, and `m_(c)=8m`. Friction is absent everywhere. String is inextensible and light. If the system is released from rest, then

Acceleration of Block A in horizontal direction is
View SolutionStudy in fig. and answer the following questions accordingly. Neglect all friction and masses of the pulleys.

What is the tension in the string?
View SolutionStudy in fig. and answer the following questions accordingly. Neglect all friction and masses of the pulleys.

What is the acceleration of block B?
View SolutionStudy in fig. and answer the following questions accordingly. Neglect all friction and masses of the pulleys.

What is the acceleration of Block A?
View SolutionThree blocks A, B, and C of masses `3M, 2M`, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is `a_(1), a_(2)` and `a_(3)` , respectively, then

The value of acceleration `a_(3)` at the moment spring PQ is cut is
View SolutionThree blocks A, B, and C of masses `3M, 2M`, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is `a_(1), a_(2)` and `a_(3)` , respectively, then

The value of acceleration `a_(1)` at the moment string RS is cut is
View SolutionThree blocks A, B, and C of masses `3M, 2M`, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is `a_(1), a_(2)` and `a_(3)` , respectively, then

The value of acceleration `a_(2)` at the moment spring TU is cut is
View SolutionIn fig, all the pulleys and strings are massless and all the surfaces are frictionless. A small block of mass m is placed on fixed wedge (take `f=10ms^(-2)`).

The tension in the string attached to m is
View SolutionIn fig, all the pulleys and strings are massless and all the surfaces are frictionless. A small block of mass m is placed on fixed wedge (take `f=10ms^(-2)`).

The acceleration of m is
View SolutionIn fig, all the pulleys and strings are massless and all the surfaces are frictionless. A small block of mass m is placed on fixed wedge (take `f=10ms^(-2)`).

The acceleration of pulley `p_(4)` is
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given `m_(1)=1kg, m_(2)= 2kg, m_(3)=3kg`.
Find the tension in the string
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given `m_(1)=1kg, m_(2)= 2kg, m_(3)=3kg`.
The acceleration of `m_(1)` is
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given `m_(1)=1kg, m_(2)= 2kg, m_(3)=3kg`.
The acceleration of `m_(3)` is
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are `1 ms^(-2)` downwards and `5ms^(-2)` downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absolute acceleration of block 1.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are `1 ms^(-2)` downwards and `5ms^(-2)` downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 2.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are `1 ms^(-2)` downwards and `5ms^(-2)` downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 3.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are `1 ms^(-2)` downwards and `5ms^(-2)` downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 4.
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected with a light spring of force constant k and the whole system is kept on a frictionless horizontal surface. The masses are applied forces `F_(1)` and `F_(2)` as shown in fig. At any time the blocks have same acceleration `a_(0)` but in opposite direction. Now answer the following :

The value of `a_(0)` is
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected with a light spring of force constant k and the whole system is kept on a frictionless horizontal surface. The masses are applied forces `F_(1)` and `F_(2)` as shown in fig. At any time the blocks have same acceleration `a_(0)` but in opposite direction. Now answer the following :

the value of spring force is
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected with a light spring of force constant k and the whole system is kept on a frictionless horizontal surface. The masses are applied forces `F_(1)` and `F_(2)` as shown in fig. At any time the blocks have same acceleration `a_(0)` but in opposite direction. Now answer the following :

If `F_(2)` is removed at this moment, then just after the acceleration of `m_(2)` is
View SolutionTwo smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases `F(theta = 37^(@)` with horizontal).
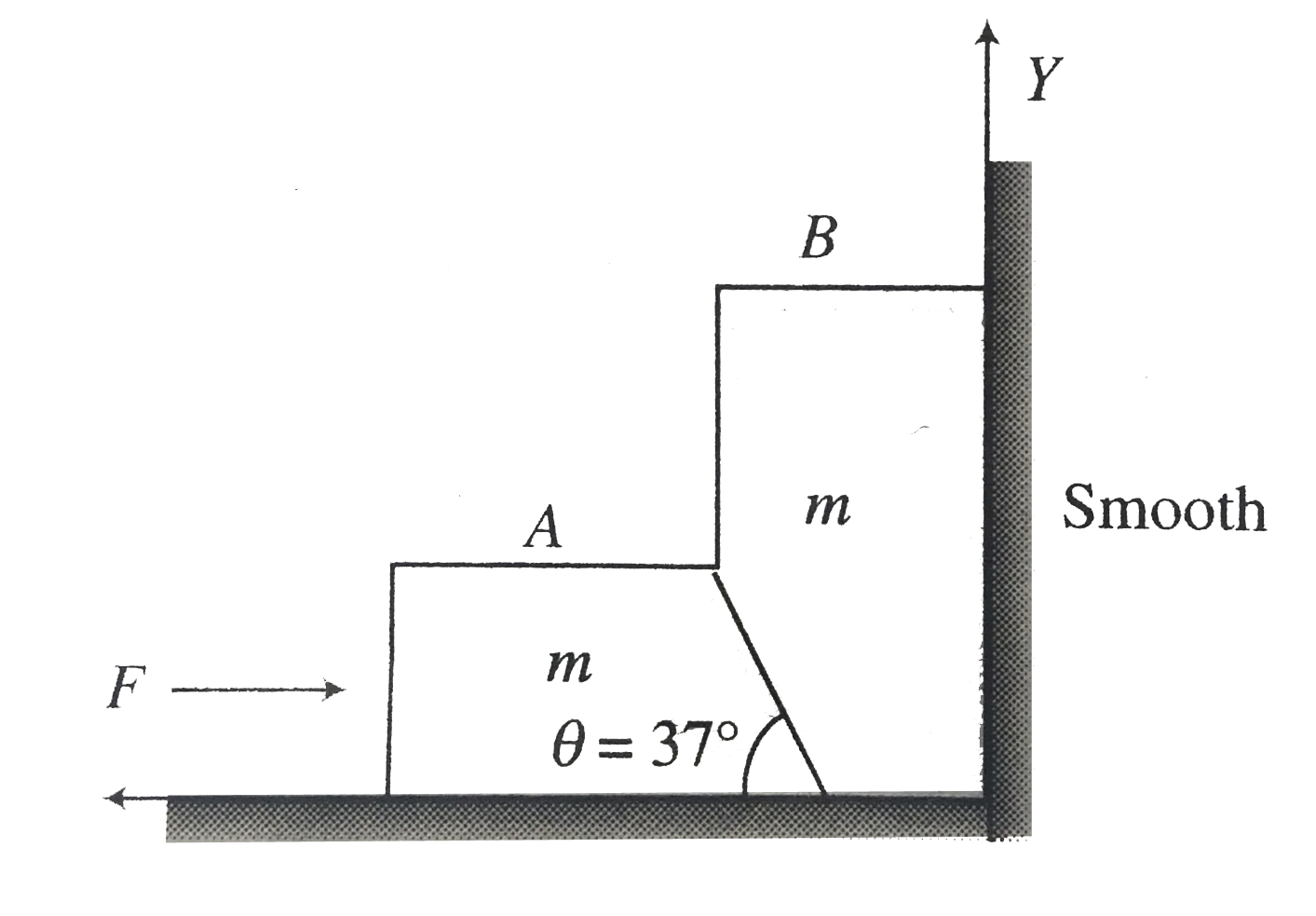
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
What is the minimum value of F to lift block B from ground?
View SolutionTwo smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases `F(theta = 37^(@)` with horizontal).
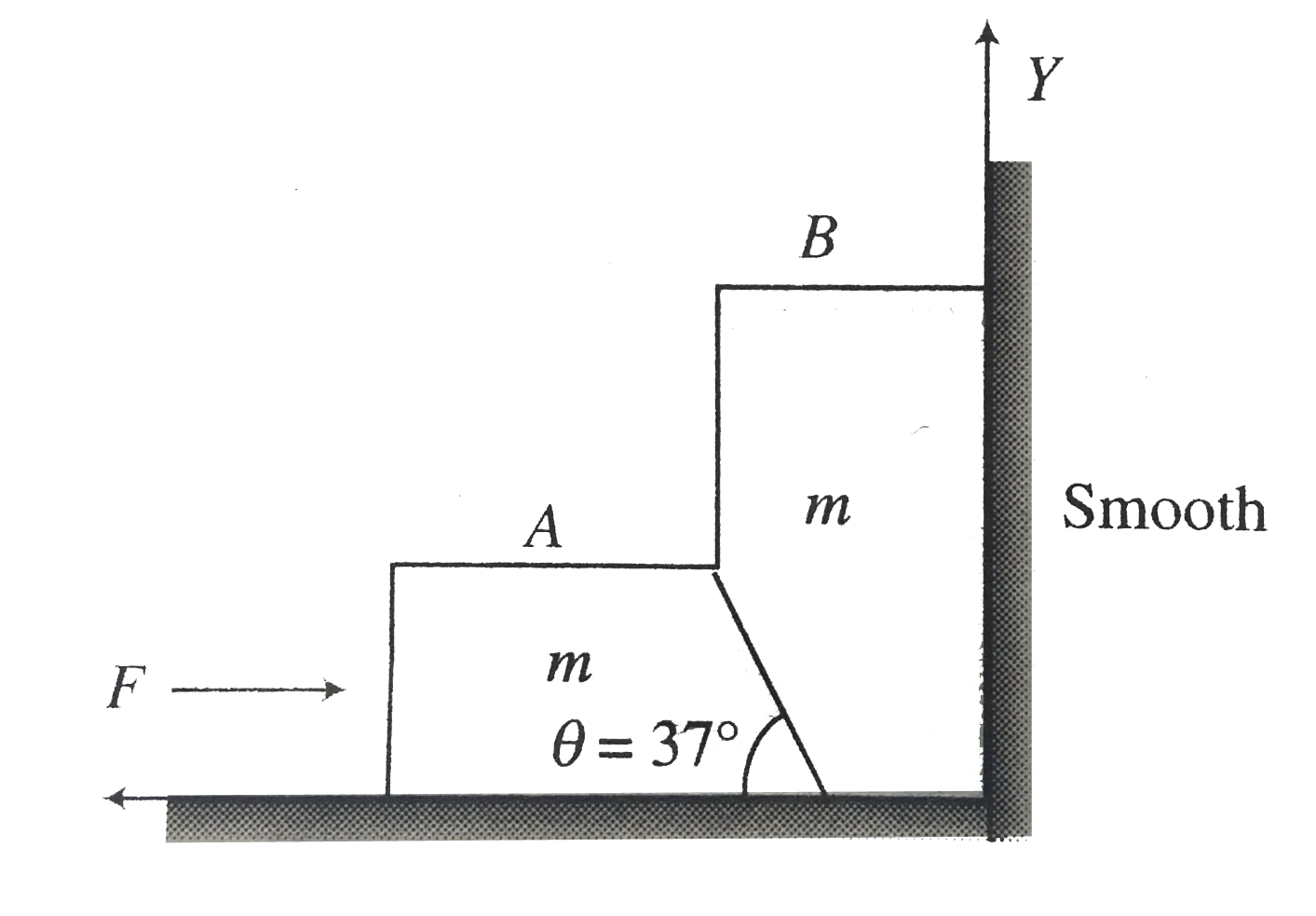
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If both the blocks are stationary, the force exerted by ground of block A is
View SolutionTwo smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases `F(theta = 37^(@)` with horizontal).
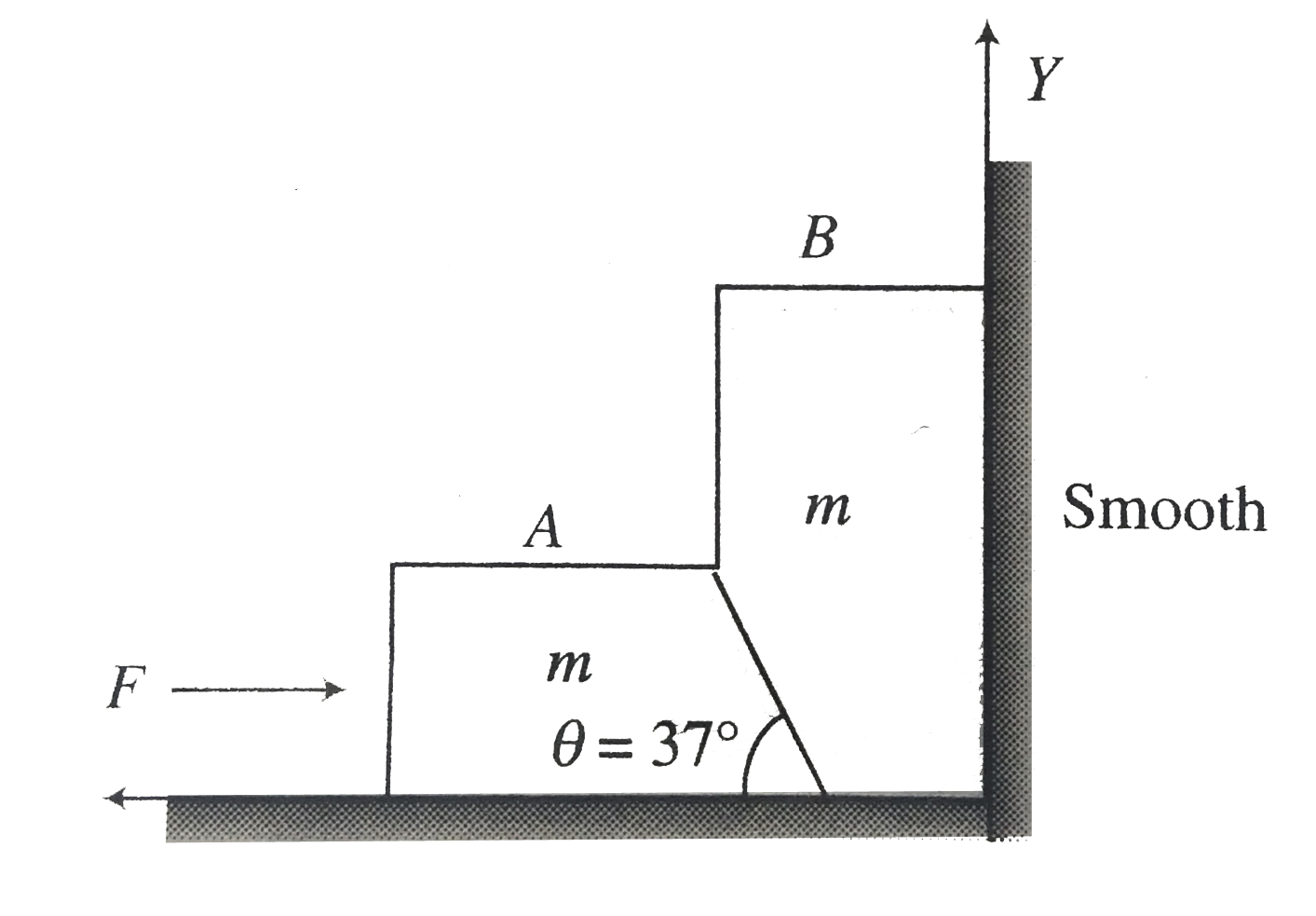
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If the acceleration of block A is a rightwards, then the acceleration of block B will be
View SolutionTwo containers of sand are arranged like the block as shown in fig. the containers alone have negligible mass, the sand in them has a total mass `M_("tot")` , the sand in the hanging container H hs mass m.

To measure the magnitude a of the acceleration of the system, a large number of experiments carried out where m varies from experiment to experiment but `M_("tot")` does not, that is, sand in shifted between the containers before each trial .
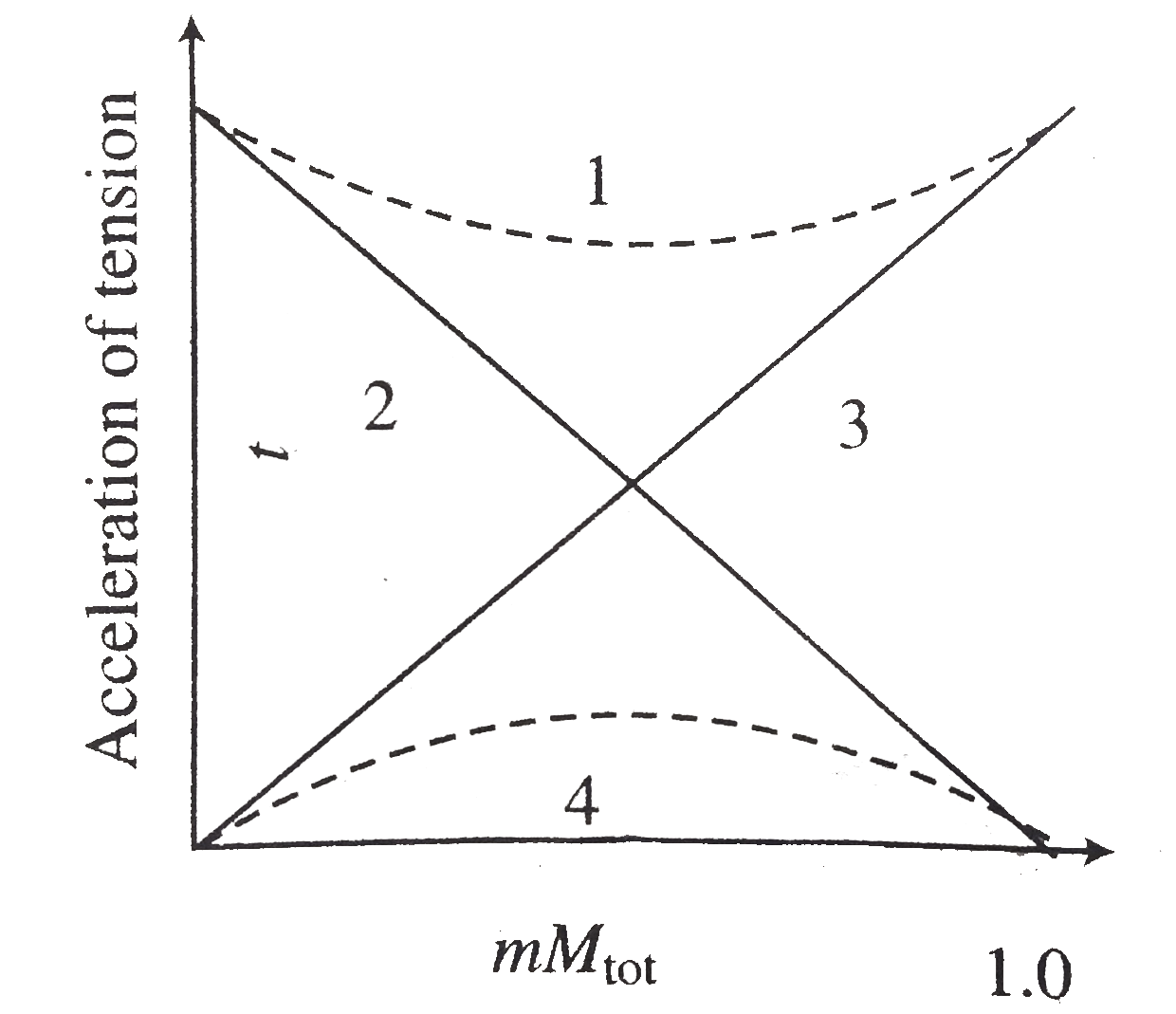
Which of the curves in graph correctly gives acceleration magnitude as a function of the ratio `m//M_("tot")` (vertical axis is for acceleration)?
View SolutionTwo containers of sand are arranged like the block as shown in fig. the containers alone have negligible mass, the sand in them has a total mass `M_("tot")` , the sand in the hanging container H hs mass m.
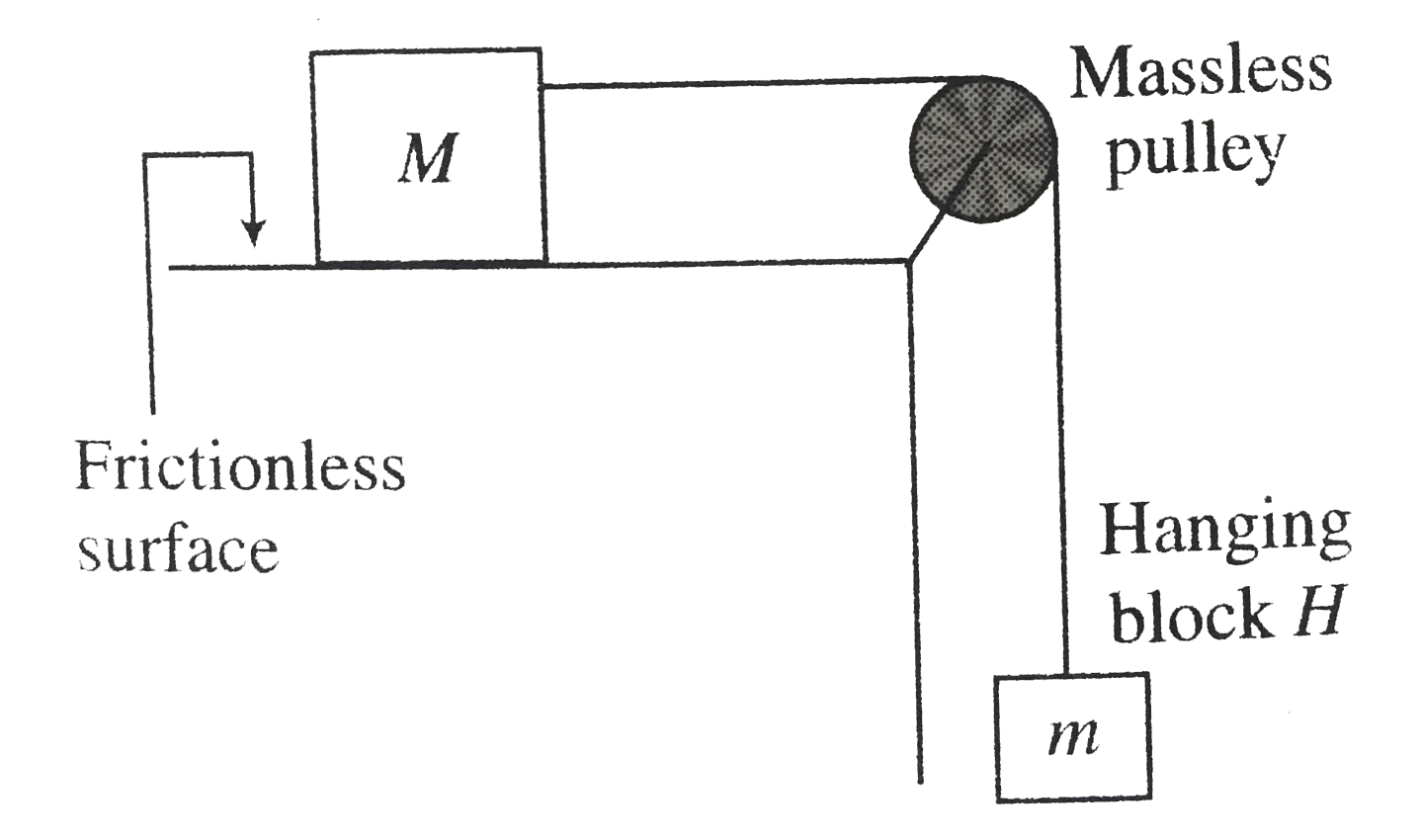
To measure the magnitude a of the acceleration of the system, a large number of experiments carried out where m varies from experiment to experiment but `M_("tot")` does not, that is, sand in shifted between the containers before each trial .
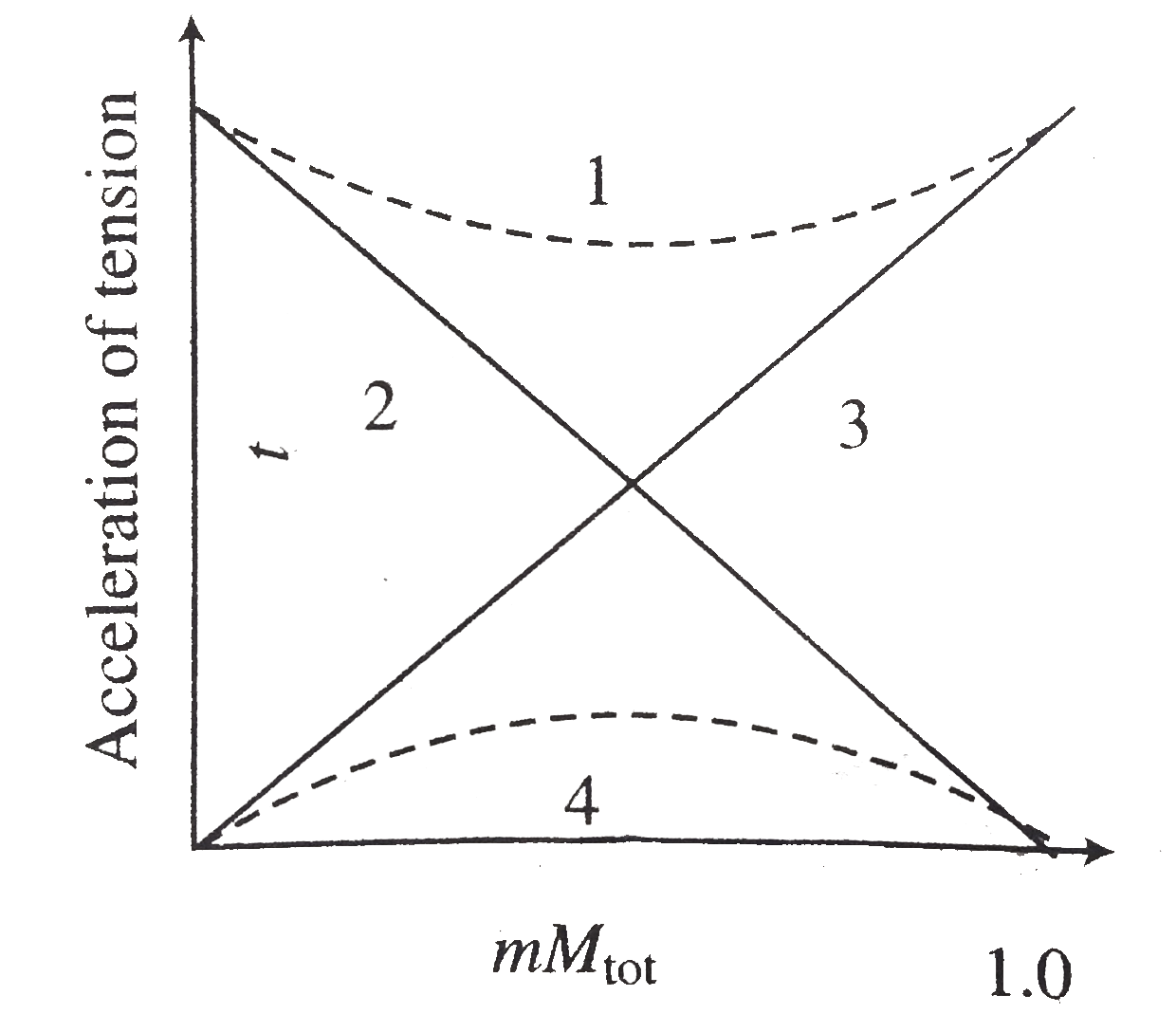
Which of them gives the tension in the connecting cord (vertical axis is for tension) ?
View SolutionA time varying force `F=6t-2t^(2)N`, at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at `t=0` the force `F=0`. Now answer the following:
Find the duration for which the force acts on the body.
View SolutionA time varying force `F=6t-2t^(2)N`, at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at `t=0` the force `F=0`. Now answer the following:
Find the time when the velocity attained by the body is maximum.
View SolutionA time varying force `F=6t-2t^(2)N`, at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at `t=0` the force `F=0`. Now answer the following:
Mark the correct statement:
View SolutionFor the system shown in fig, there is no friction anywhere. Masses `m_(1) and m_(2)` can move up or down in the slots cut in mass M. Two non-zero horizontal force `F_(1)` and `F_(2)` are applied as shown. The pulleys are massles and frictionless. Given `m_(1) != m_(2)`

According to the above passage, which is correct?
View SolutionFor the system shown in fig, there is no friction anywhere. Masses `m_(1) and m_(2)` can move up or down in the slots cut in mass M. Two non-zero horizontal force `F_(1)` and `F_(2)` are applied as shown. The pulleys are massles and frictionless. Given `m_(1) != m_(2)`

Let `F_(1)` and `F_(2)` are applied in such a way that `m_(1) and m_(2)` do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let `m_(1) gt m_(2)`.
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected with a light spring of force constant k and the whole system is kept on a frictionless horizontal surface. The masses are applied forces `F_(1)` and `F_(2)` as shown in fig. At any time the blocks have same acceleration `a_(0)` but in opposite direction. Now answer the following :

the value of spring force is
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
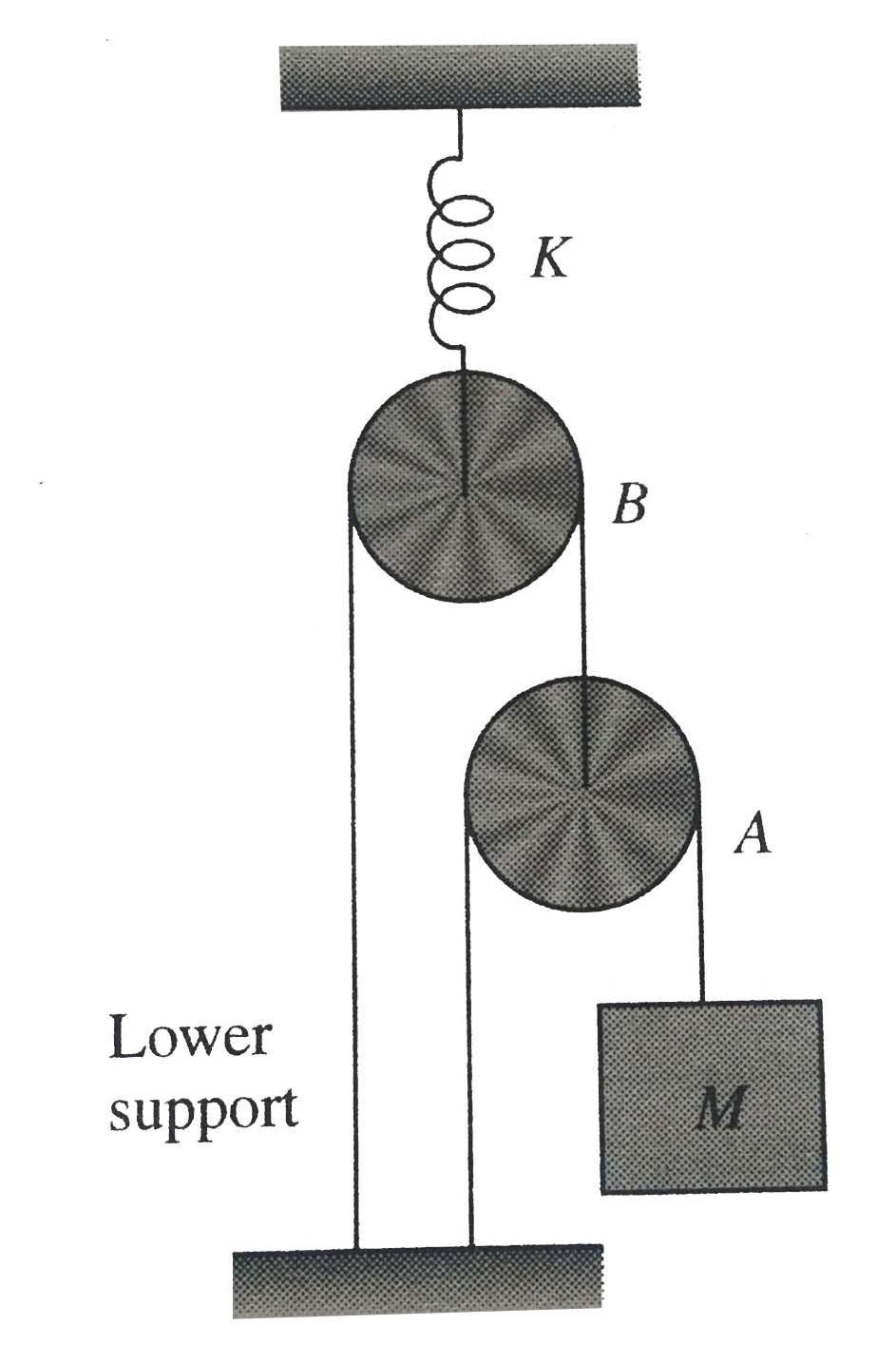
The extension produced in the spring is given by
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
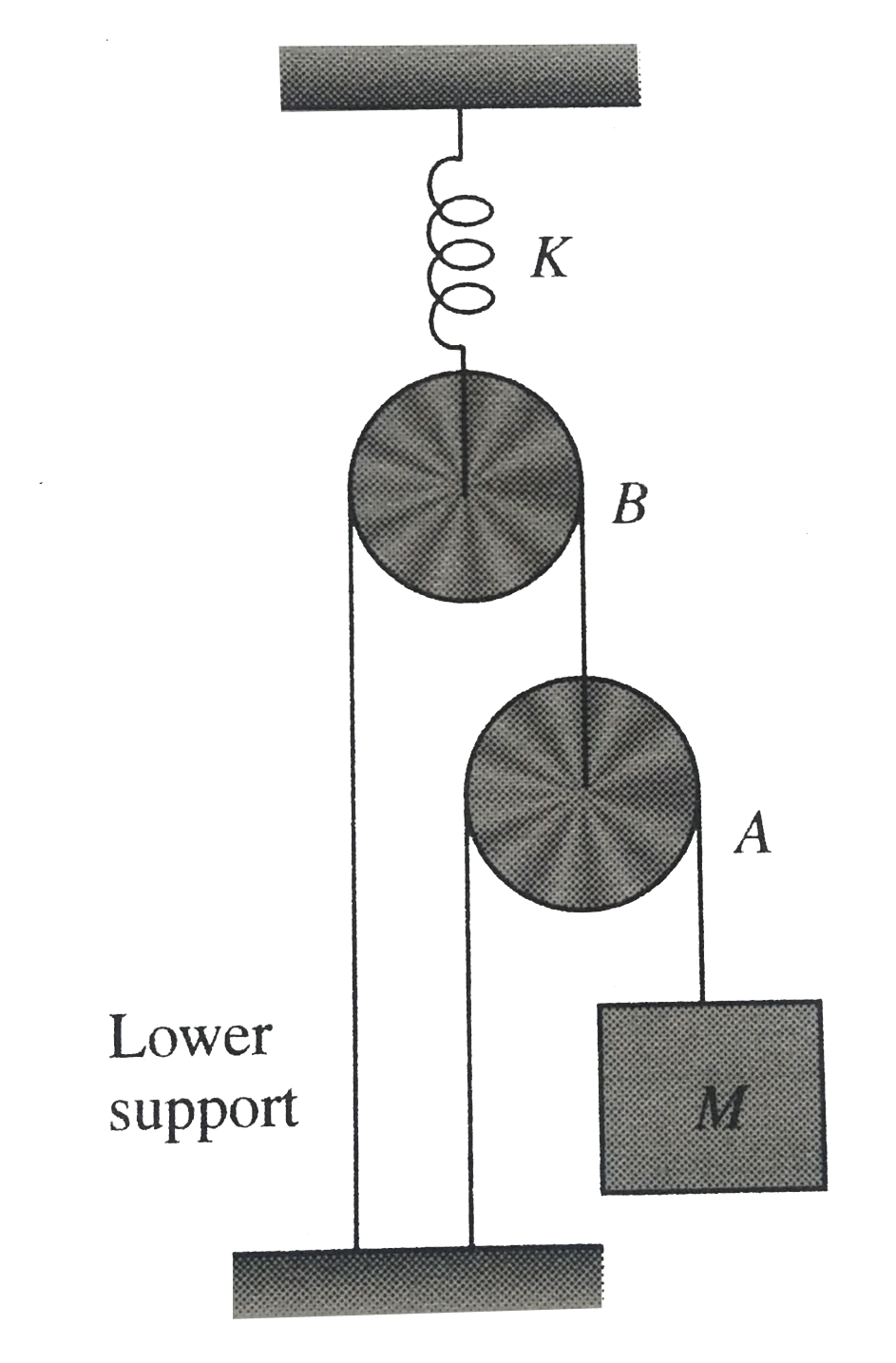
Find the net tension force acting on the lower support.
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.

If each of the pullies A and B has mass M, then find the net tension force acting on the lower support. Asumme pulleys to be frictionaless.
View Solution
Linked Comperhension questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 1 of CENGAGE PHYSICS (HINGLISH) of Class 11