Complete Solutions to Illustrations of chapter NEWTON'S LAWS OF MOTION 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 1 |
| CENGAGE PHYSICS | Illustrations |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
In a paricular crash test, a car of mass 1500 kg collies with a wall as shown in fig. The initial and final velocites on the car are `vec(v_i)=-15.0 hat(i)ms^(-1)` and `vec(v_f)=5.00 hat(i) ms^(-1)`, respectively. If the collision lasts `0.150s`, find the impulse caused by the collision and the average force exerted on the car.

View SolutionA body of mass m=1kg falls from a height h=20m from the ground level .
(a) What is the magnitude of total change in momentum of the body before it strikes the ground?
(b) What is the corresponding average force experienced by it ?`(g=10ms^(-1))`
View SolutionAn iron ball of mass `m=50 g` falls from a height of `(h_1)=5m` and rises upto `h_(2)=3.2m` after colliding with the horizontal surface. If the time of contact with the surface is `Delta t=0.02s`, find the average contact force exerted on the ball by the horizontal surface.
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionTwo particle of masses 10 kg and 35 kg are connected with four strings at points B and D as shown in fig.

Determine the tension in various segments of the string.
View SolutionThree block A,B,and C of mass `m_(1),m_(2)` and `m_(3)`, respectively are resting one on top of the other as shown in fig. A horizontal force F is applied on block B. Assuming all the surfaces are frictionless, calculate (1) acceleration of block A, block B, and block C, (2) normal reactions between A and B, B and C, and between C and ground .

View SolutionThree boys, each of mass 45 kg, pull simlutaneously a block on a smooth surface. The mass of block is 20.0 kg.
(a) Find the acceleration of the block.
(b) Find the acceleration of the boy exerting force `F_(1)` . Assume no friction between the boy and the surface .

(Given `F_(1)=90N, F_(2)=114 N, and F_(3)=128sqrt(2)N]`.
View SolutionA block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle `theta=37^(@)`, with horizontal as shown in fig. find the acceleration of the block at the given instant.

View SolutionTwo block of masses `m_(1) and m_(2)` are placed side by side on a smooth horizontal surface as shown in fig. A horizontal force F is applied on the block .

(a) Find the acceleration of each block.
(b) Find the normal reaction between the two blocks.
View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied on a 1-kg block. Find the force of interaction of the blocks.

View SolutionFind the force of interaction between the bodies as shown in fig. Blocks are in contact.

View SolutionA solid sphere of mass 2 kg is resting inside a cube as shown in fig. The cube is moving with a velocity `vec(v)=(5t hat(i)+2t hat(j))ms^(-1)`. Here t is time in seconds. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force (in N) exerted by the sphere on the cube?

View SolutionIn the arrangement shown in fig. The strings are light and inextensible. The surface over which blocks are placed is smooth. Find:

(a) the acceleration of each block.
(b) the tension in each string.
View SolutionTwo mass `m_(1) and m_(2)` are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

View SolutionIn fig.block A and B are connected together by a string and placed on a smooth inclined plane. B is connected to C(which is suspended vertically) by another string which passes over a smooth pulley fixed to th plane. The mass A is `m_(A)=1` kg and mass of B is `m_(B)=2 kg`.

(a) If the system is at rest, find the mass of C.
(b) If the mass of C is twice the mass calculate in (a) then find the acceleration of the system.
View SolutionBlock A of mass `m//2` is connected to one end of light rope which passes over a pulley as shown in fig. A man of mass m climbs the other end of rope with a relative acceleration of `g//6` with respect to rope. Find the acceleration of block A and tension in the rope.

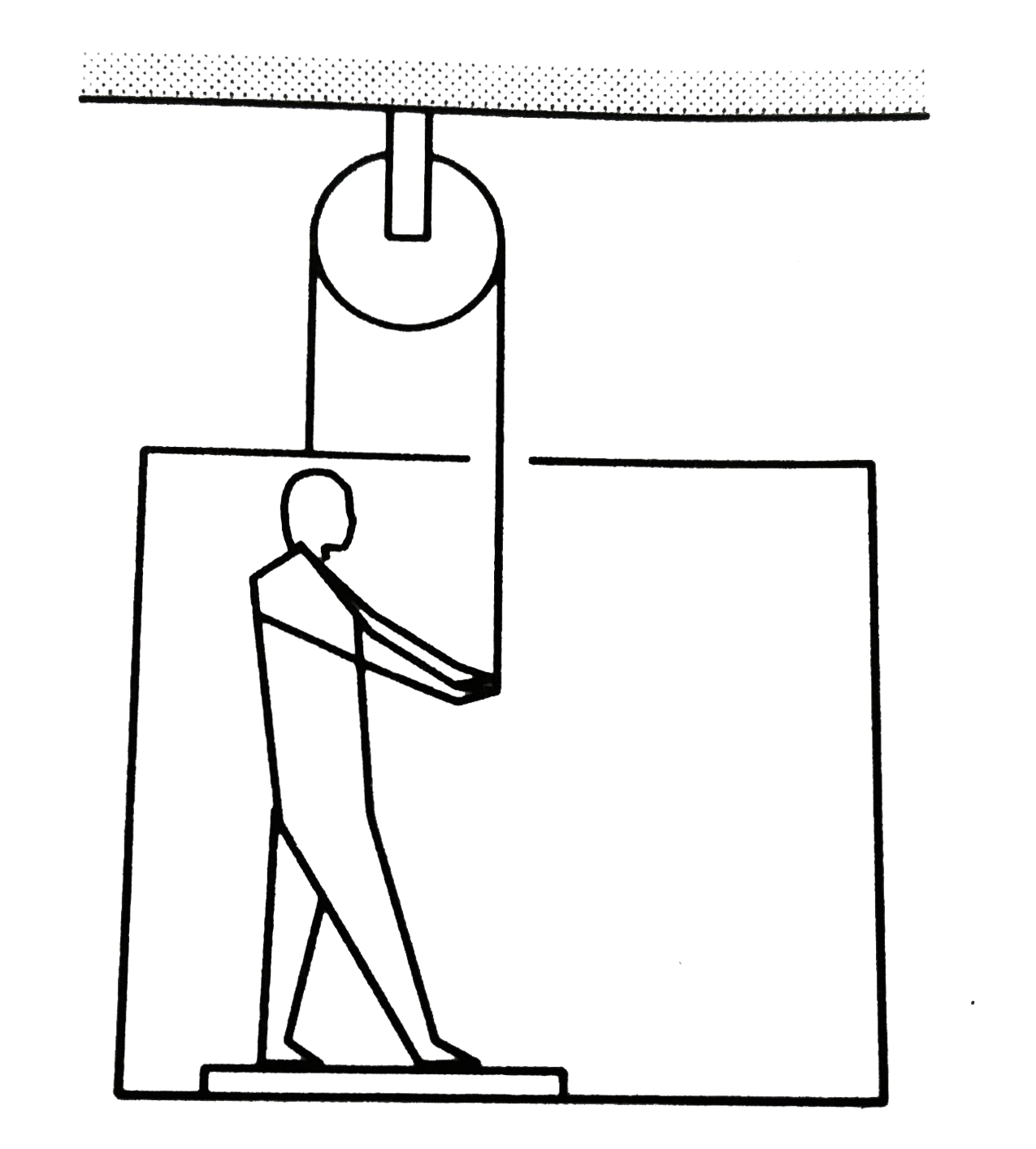
View SolutionFigure shows a man of mass 60 kg standing on a light weighting machine kept in a box of mass 30 kg. The box is haning from a pulley fixed to the ceiling through a light rope, the other end of which is held by the man himswelf. If the man manages to keepthe box at rest, what is the weight shown by the man manages to keep the box at rest, what is the weight shown by the machine? What force should he exert on the rope to get his correct weight on the machine?
View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

View SolutionA homogeneous flexible rope rests on a wedge whose side edges make angles `alpha` and `beta` with the horizontal. The central part of the rope lies on the upper rib C of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge? [Consider all surfaces to be smooth]

View SolutionThe block of mass m is in equilibrium relative to the smooth wedge of mass M which is pushed by a horizontal force F. Find pseudo force acting on (a) m, (b)M as viewed by the observer sitting on the wedge. Will these pseudo forces (c ) equal and opposite, action reaction pairs? Explain.

View SolutionA rail-road car is moving towards right with acceleration a. A man accelerating toward left with an acceleration of magnitude `a//3` w.r.t to car. A dog of mass m is following man A with an acceleration `a//3` relative to the car. Observer B on ground is observing the dog and man A. Find the
(a) net force experienced by the dog as seen by observer B standing on ground.
(b) rate of change of linear momentum of the dog relative to the man A moving on trolley.
(c ) pseudo-free on the dog as seen from man A.

View SolutionA man of mass M stands on a weighing machine in an elevator accelerating upwards with an acceleration a. Draw the free-body diagram of the man as observed by the observer A (stationary on the ground) and observer B (stationary on the elevator). Also, calculate the reading of the weighing machine.

View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle `thata=37^(@)` with the vertical. Find the acceleration of the trolley.

View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration `a_(0)` in direction forming angle `alpha` with the rod as shown. The acceleration of bead with respect to rod is:
`z`
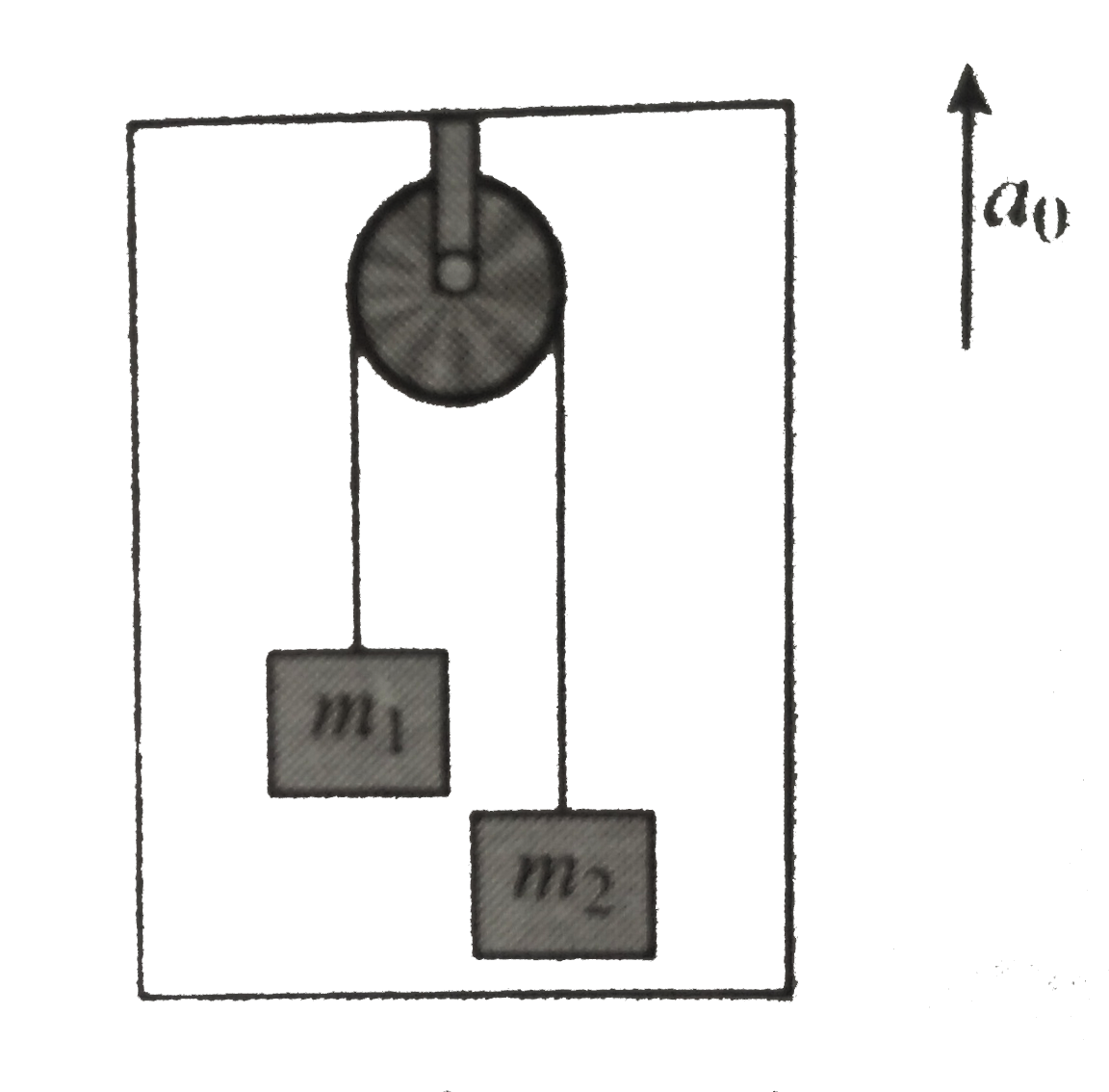
View SolutionIf the pulley is massles and moves with an upward acceleration `a_(0)`. Find the acceleration of `(m_1)and (m_2)` w.r.t to elevator.
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.

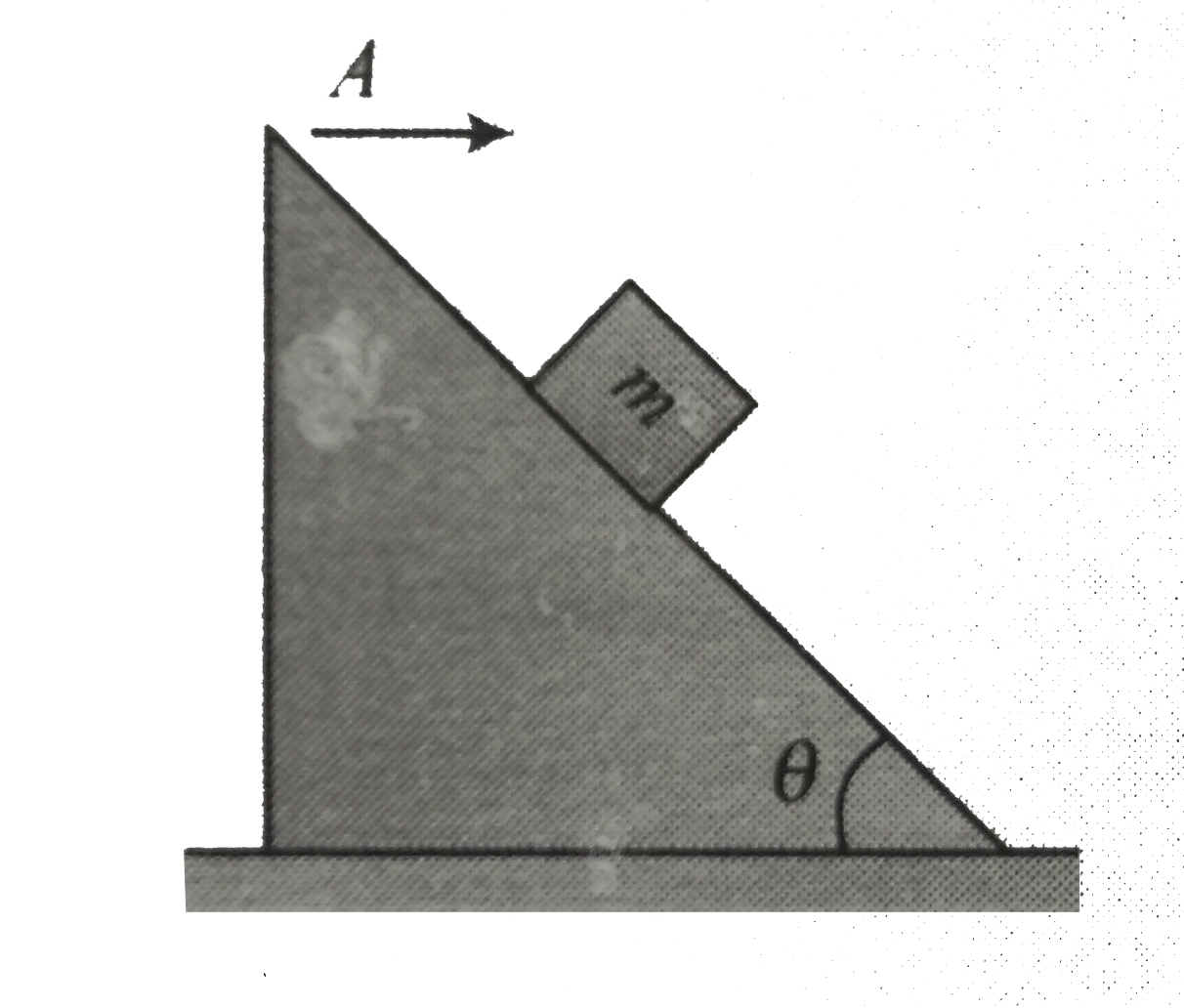
View SolutionA block of mass m is placed on an inclined plane. With what acceleration A towards right should the system move on a horizontal surface so that m does not slide on the surface of inclined plane? Also calculate the force supplied by wedge on the block. Assume all surfaces are smooth.
View SolutionIn the arrangement of three block as shown in fig. the string is inextensible. If the direction of accelerations are as shown in the figure, then determine the constraint relation.

View SolutionA pulley-rope-mass arrangement is shown in fig. Find the acceleration of block `m_(1)` when the masses are set free to move. Assume that the pulley and the ropes are ideal.
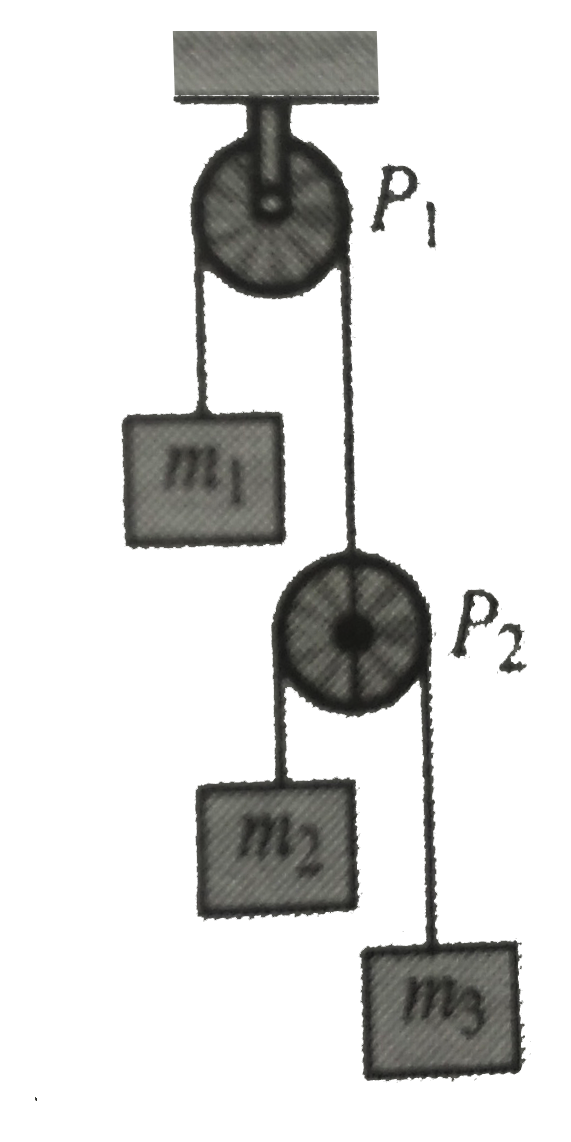
View SolutionA pulley-rope-mass arrangement is shown in fig. Find the acceleration of block `m_(1)` when the masses are set free to move. Assume that the pulley and the ropes are ideal.

View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionIn fig. mass `m` is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

View SolutionA rod of mass m is supported on a wedge of mass M shown in fig. Find the accelerations of rod a and wedge A in the arrangment. The friction between all contact surfaces in negligible.

View SolutionA plank of mass m rests symmetrically on two wedges B and C of mass M. What is the acceleration of the plank? Neglect friction between all the contact surfaces.

View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle `theta` with the horizontal.

View SolutionIn fig. a ball of mass `m_(1)` and a block of mass `m_(2)` are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If `v_(1)` and `v_(2)` are the respective speeds of the ball and the block, then determine the constraint relation between the two.
View SolutionThe ring `M_(1)` and block `M_(2)` are held in the position shown in fig. Now the system is released. If `M_(1) gt M_(2)`, find `V_(1)//V_(2)` wheb the ring `m_(1)` slides down along the smooth fixed vertical rod by the distance h.
View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length `3R//4` is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of `60^@` with the vertical. The spring constant `K=mg//R`. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

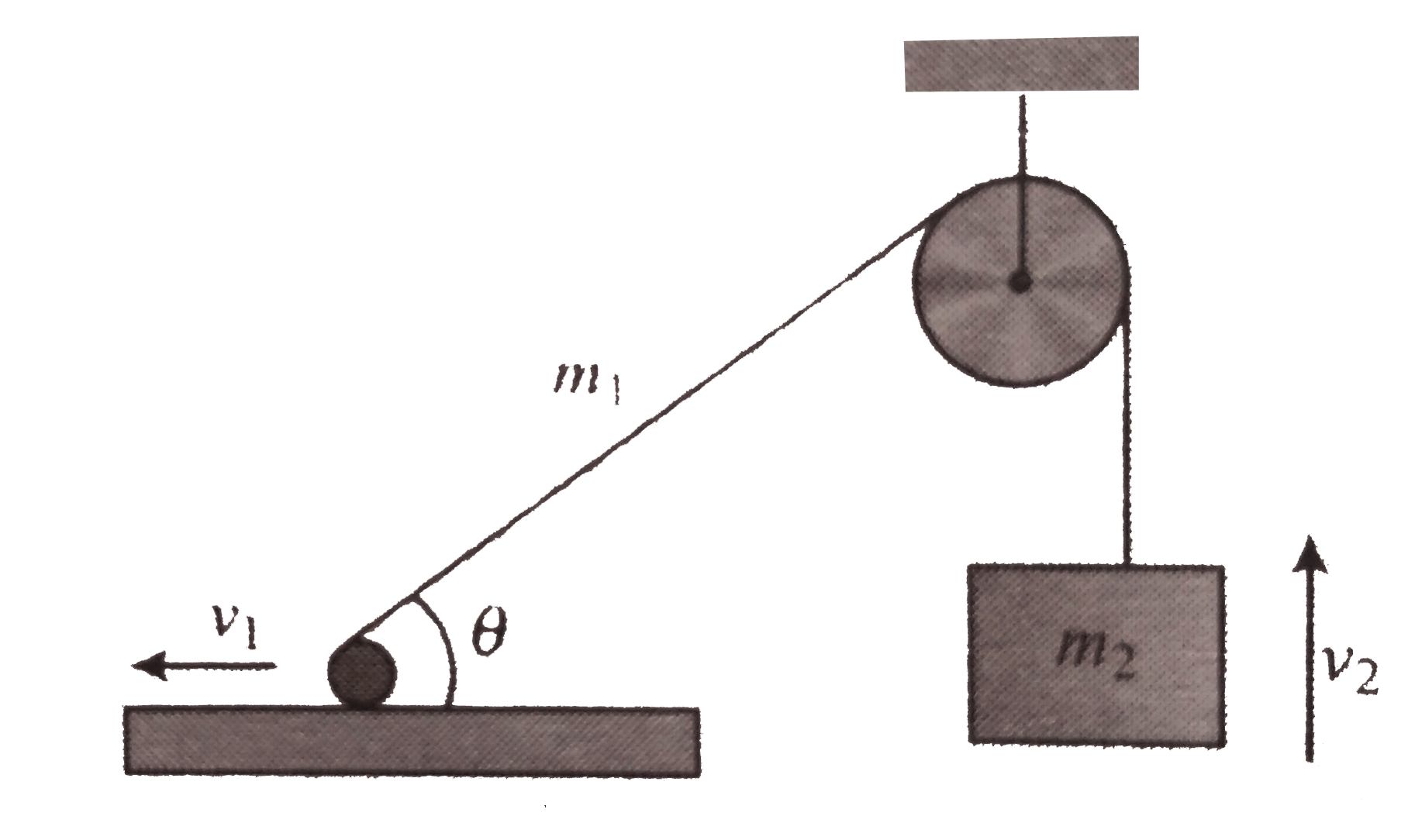
View SolutionTwo disks of masses `m_(1)` and `m_(2)` are connected by a spring of force canstant k. The lower disk of mass `m_(2)`lies on a table and the upper disk is vertically above it. What vertical force F should be applied to the upper disk so that when the force is withdraw, the lower disk is lifted off the table?
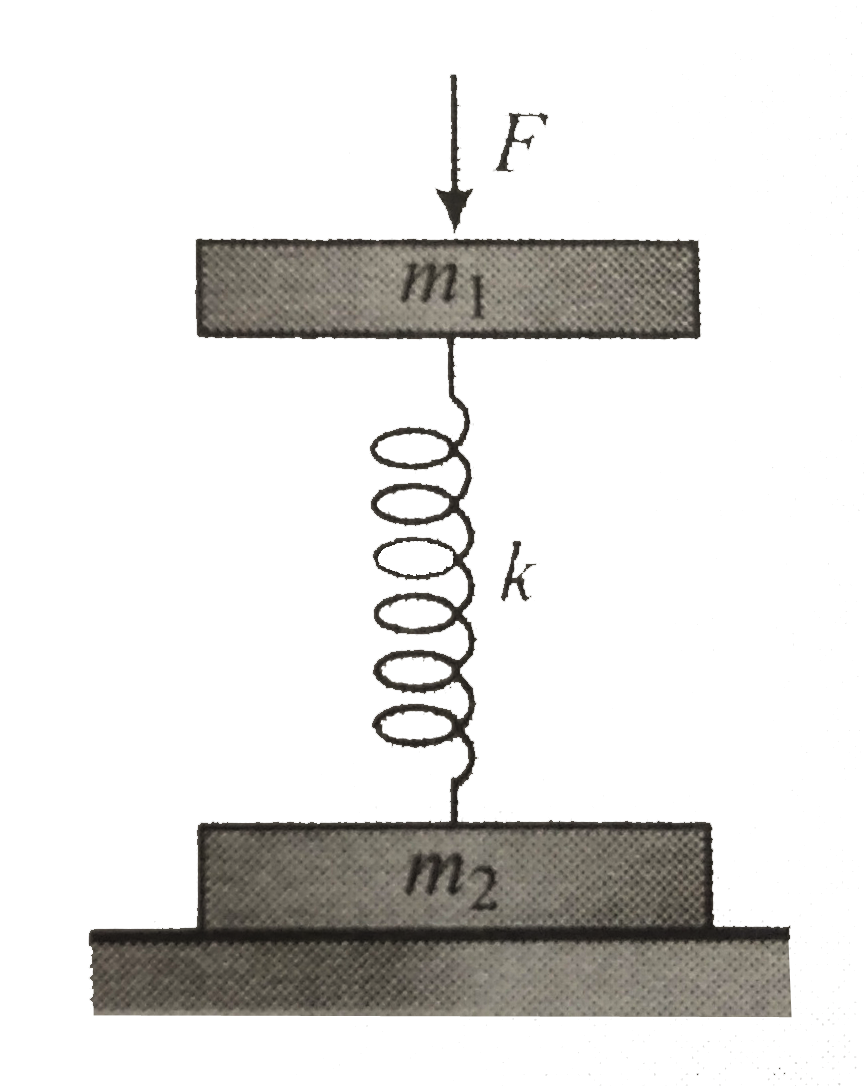
View SolutionOn applying a force F, point P is displaced vertically down by y from equilibrium positionl. Find force F in terms of the force constant k of the spring and displacement y, for the cases (a) and (b), as shown in fig.

View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
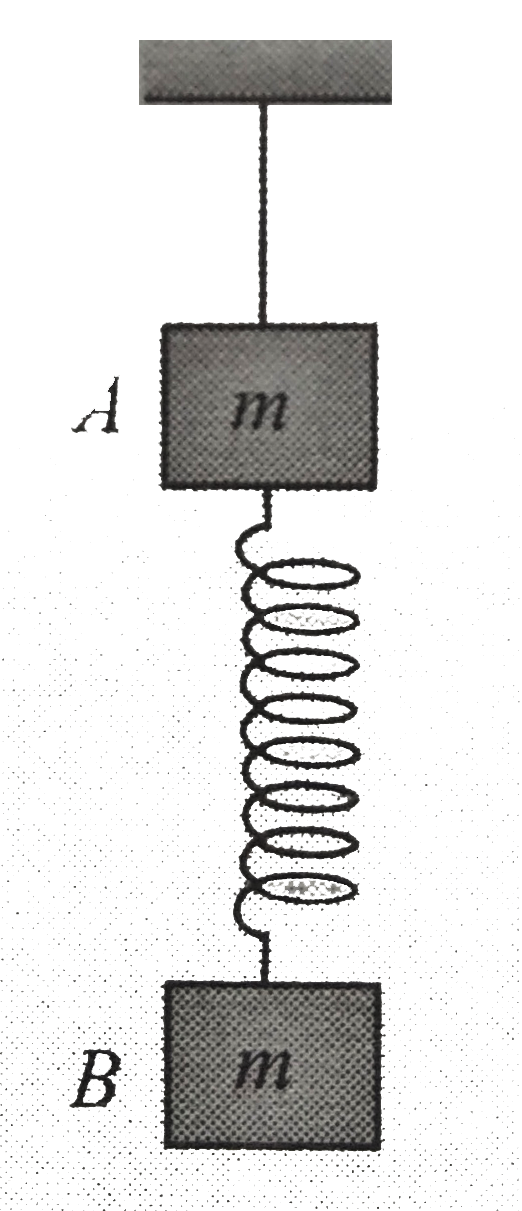
View SolutionThe system of two weights with masses `M_(1)` and `M_(2)` are connected with weightless spring as shown in fig. The system is resting on the support S. Find the acceleration of each of the weights just after the support S is quickly removed.
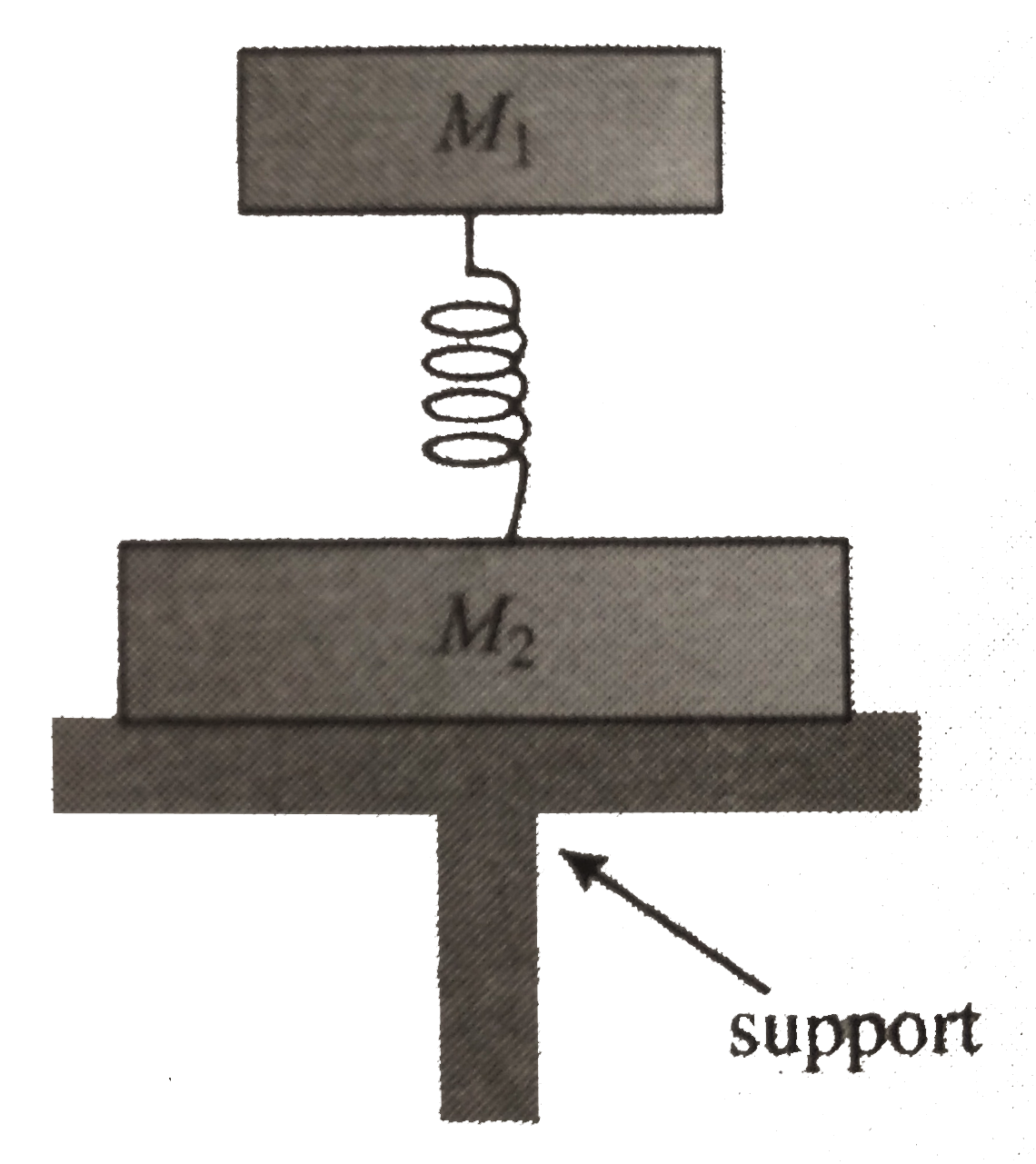
View SolutionFour blocks and two springs are arranged as shown in fig. The system at rest, determine the accelration of all the loads immedialtely after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless, the mass of the pulley is negligible small, and there is no friction at the point of suspension.

View SolutionThree blocks A, B, and C of masses `3M, 2M`, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is `a_(1), a_(2)` and `a_(3)` , respectively, then

The value of acceleration `a_(3)` at the moment spring PQ is cut is
View Solution
Illustrations questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 1 of CENGAGE PHYSICS (HINGLISH) of Class 11