Complete Solutions to Single Correct of chapter NEWTON'S LAWS OF MOTION 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 1 |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
Two skaters have weight in the ratio `4:5` and are 9m apart, on a smooth frictionless surface. They pull on a rope stretched between them. The ratio of the distance covered by them when they meet each other will be
View SolutionWhen forces `F_1`, `F_2`, `F_3`, are acting on a particle of mass m such that `F_2` and `F_3` are mutually perpendicular, then the particle remains stationary. If the force `F_1` is now removed then the acceleration of the particle is
View Solutionn balls each of mass m impinge elastically each second on a surface with velocity u. The average force experienced by the surface will be
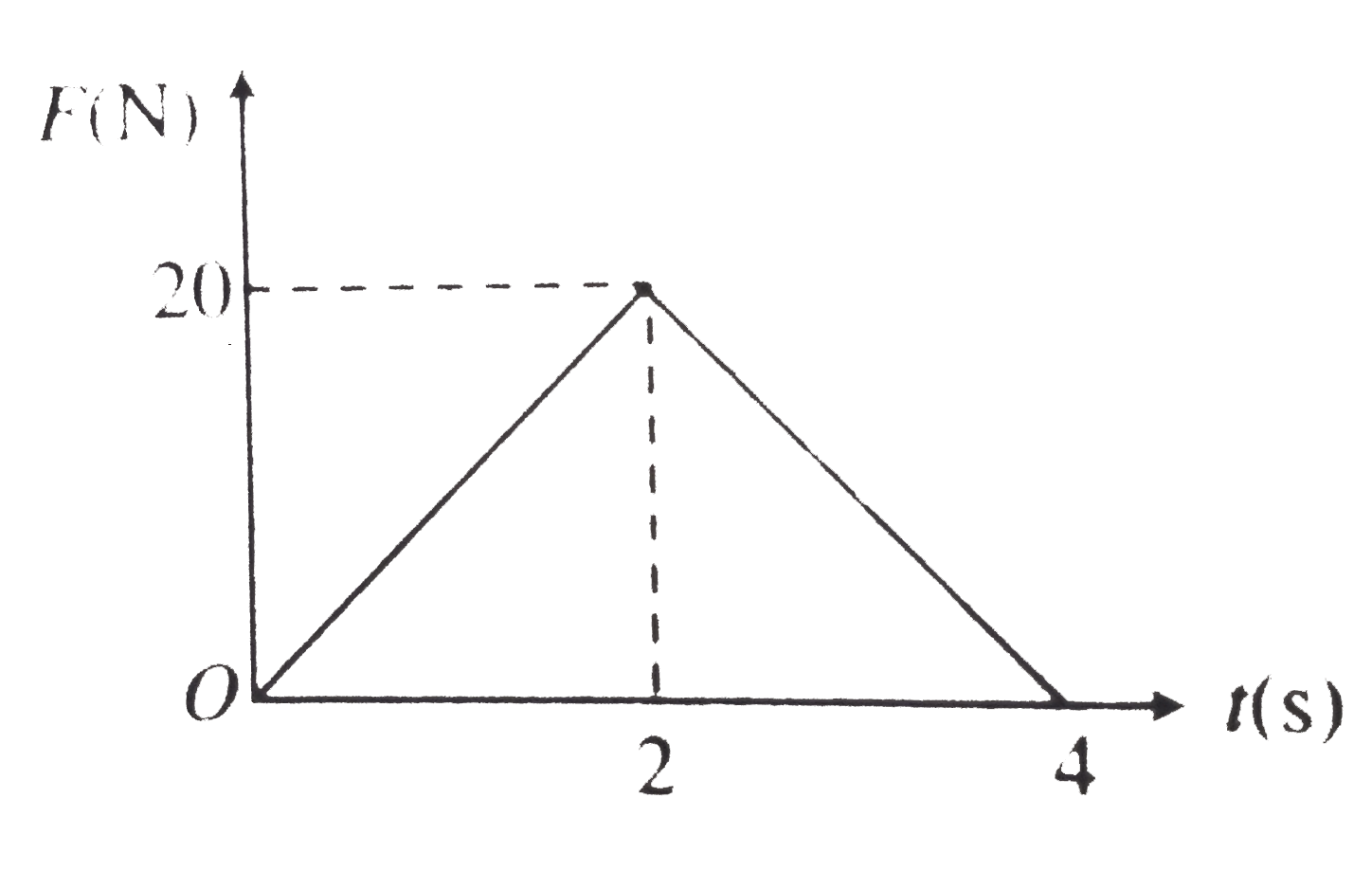
View SolutionA particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass `m`. They come in contact for a very small time `t_0`. Their force of interaction increases from zero to `F_0` linearly in time `0.5t_0`, and decreases linearly to zero in further time `0.5t_0` as shown in figure. The magnitude of `F_0` is
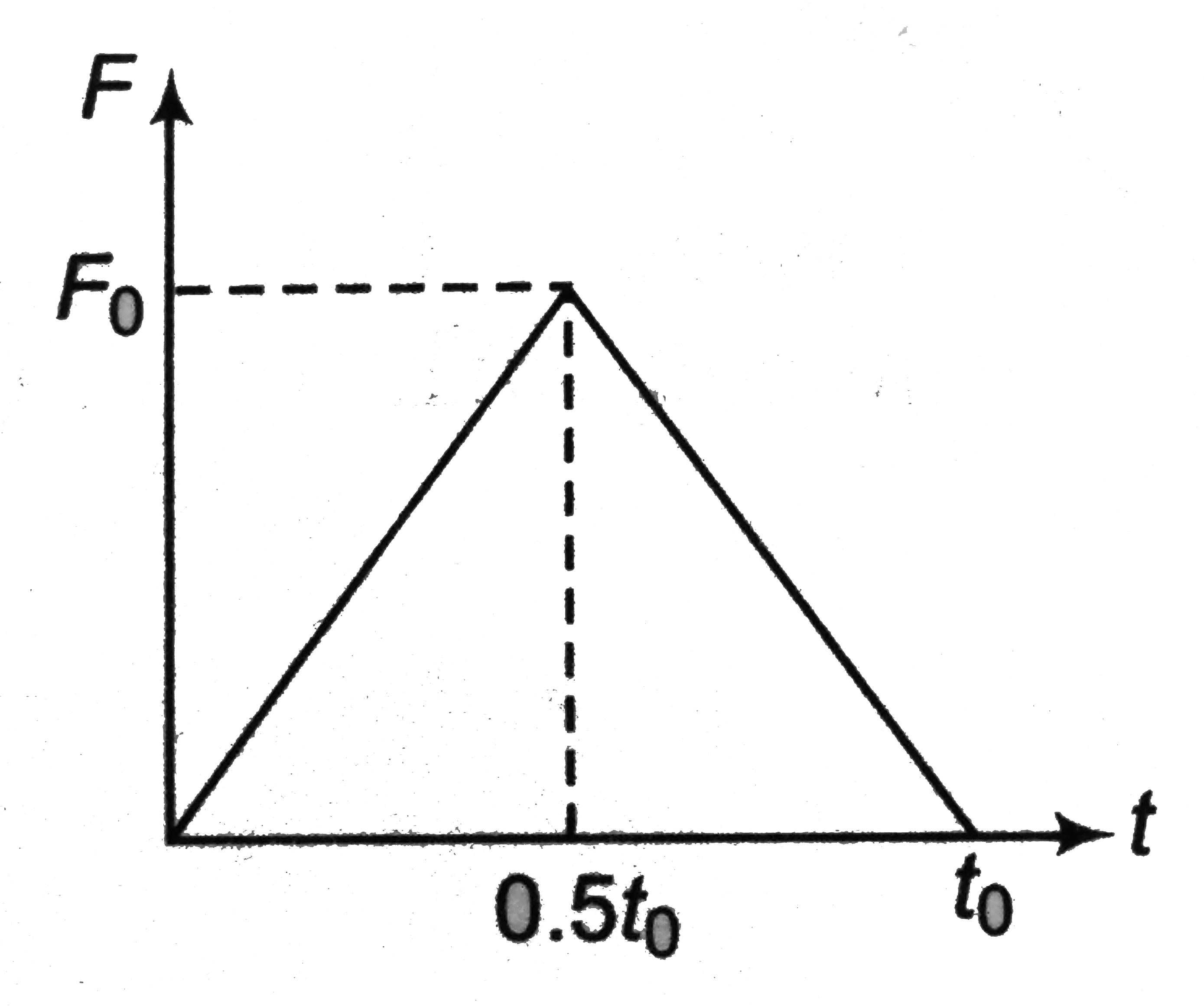
View SolutionIn order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration `5g//4` relative to the rope. The tension in the rope is (take `g=10 ms^(-2)`)

View SolutionA plumb bob of mass `1 kg` is hung from the ceiling of a train compartment.The train moves on an inclined plane with constant velocity. If the angle of inclined is `30^(@)`.Find the angle made by the string with the normal to the ceiling .Also ,Find the tension in the string `(g = 10 m//s^(2))`
View SolutionConsider the system shown in fig. the system is released from rest, find the tension in the cord connected between 1kg and 2 kg blocks.

View SolutionA balloons of mass M is descending at a constant acceleration `alpha`. When a mass m is released from the balloon, it starts rising. With the same acceleration `alpha`. Assuming that its volumes does not change, what is the valule of m?
View SolutionA trolley of mass 5 kg on a horizontal smooth surface is pulled by a load of mass 2 kg by means of uniform rope ABC of length 2 m and mass 1kg. As the load falls from BC=0 to BC=2m. Its accerleration in `m//s^(2)` change-

View SolutionAll surfaces are smooth in following figure. Find `F`, such that block remain stationary with respect to wedge.

View SolutionA Bead of mass `m` is attached to one end of a spring of natural length `'R'` and spring cosntant `'k=((sqrt3+1)mg)/R'`. The other end of the spring is fixed at point `'A'` on a smooth vertical ring of radius `'R'` as shown
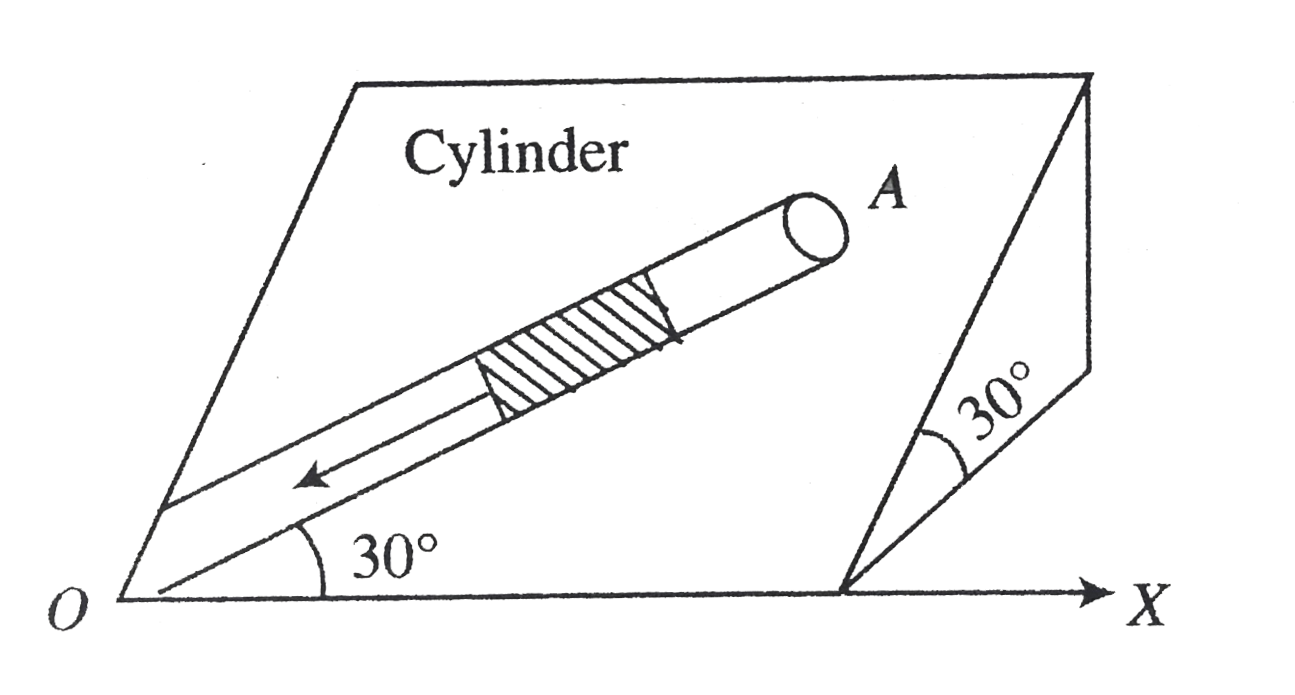
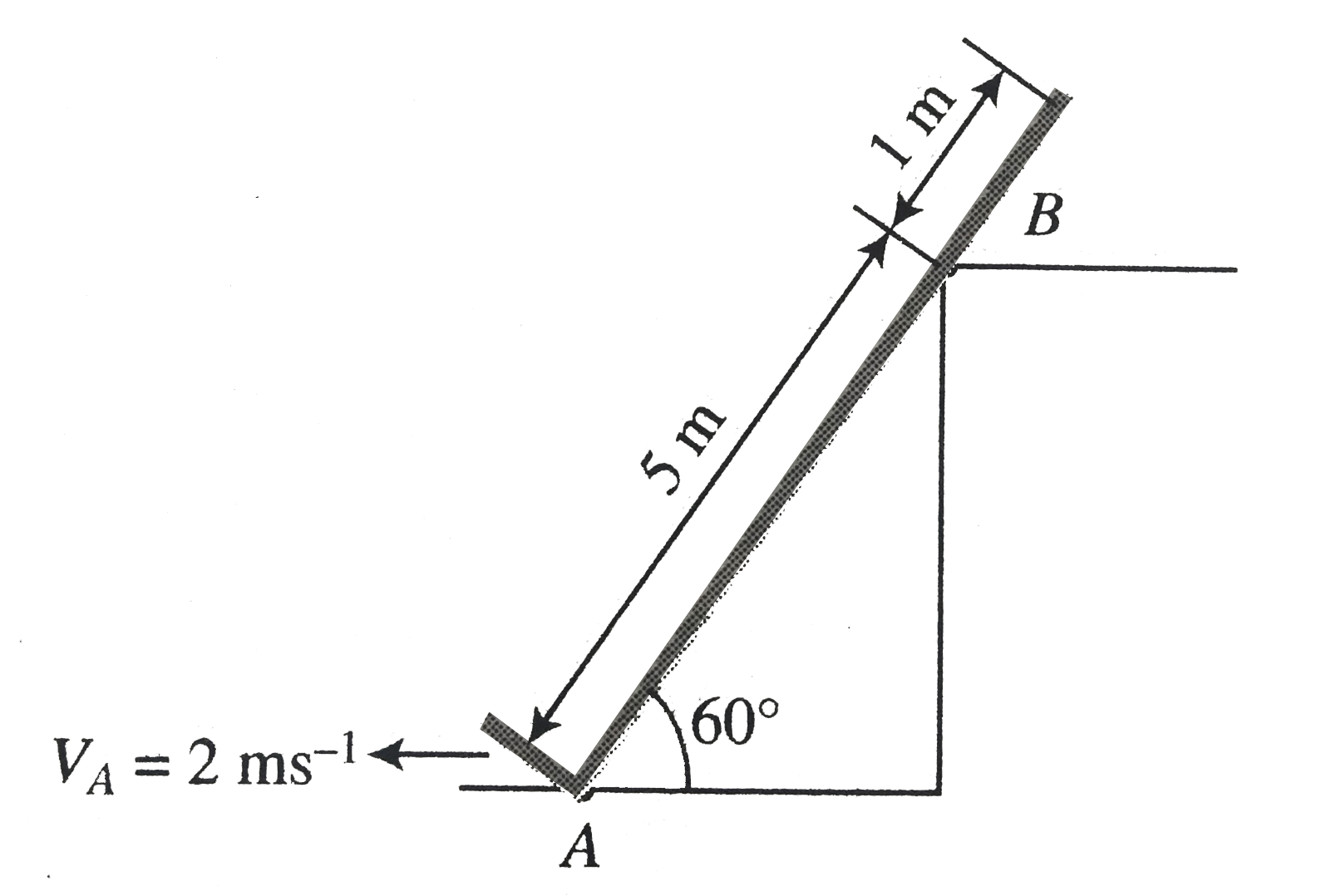
View SolutionAn inclined plane makes an angle `30^(@)` with the horizontal. A groove (OA) of length 5m cut in the plane makes an angle `30^(@)` with OX. A short smooth cylinder is free to slide down under the influence of gravity. The time taken by the cylinder to reach from A to O is `(g=10ms^(-2))`.
View SolutionA man is raising himself and the crate on which he stands with an acceleration of `5ms^(-2)` by a massless rope-and-pulley arrangement. Mass of the man is 100kg and that of the crate is 50 kg. If `g=10ms^(-2)`, then the tension in the rope is
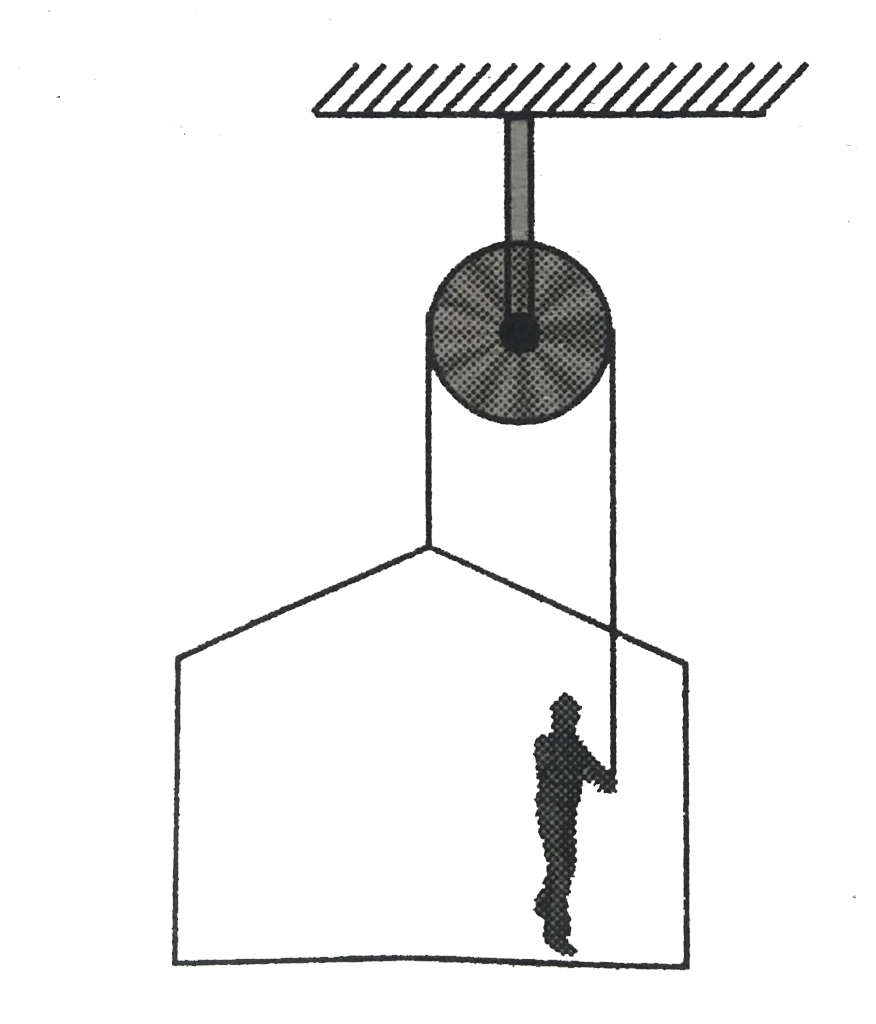
View SolutionIn the above problem, the contact force between the man and the crate is
View SolutionTwo beads of equal masses `m` are attached by a string of length `sqrt2a` and are free to move in a smooth circular ring lying in a vertical plane as shown in figure. Here a is the radius of the ring. Find the tension and acceleration of `B` just after the beads are released to move.

View SolutionBlock A and C starts from rest and move to the right with acceleration `a_(A)=12tms^(-2)` and `a_(C )=3ms^(-2)`. Here t is in second. The time when block B again comes to rest is
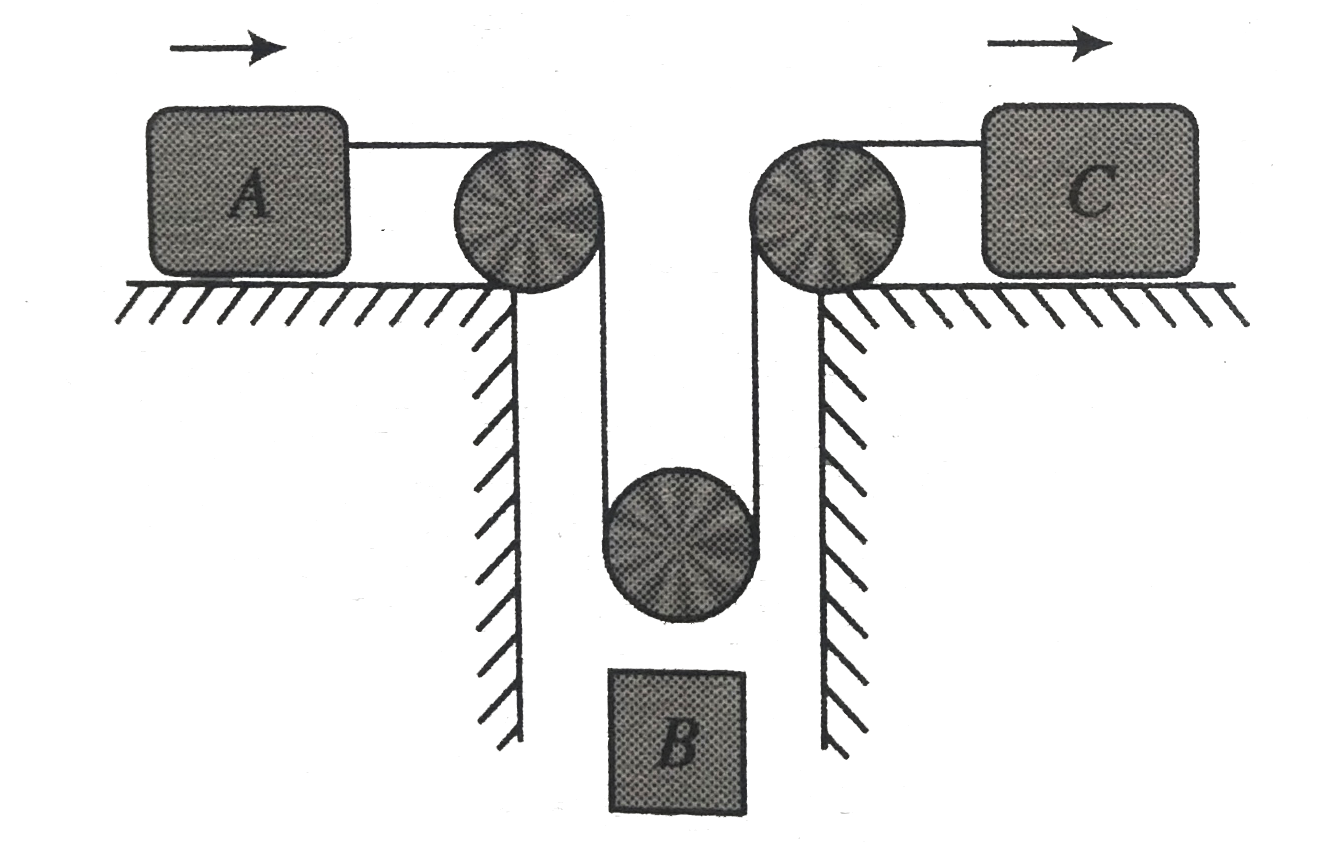
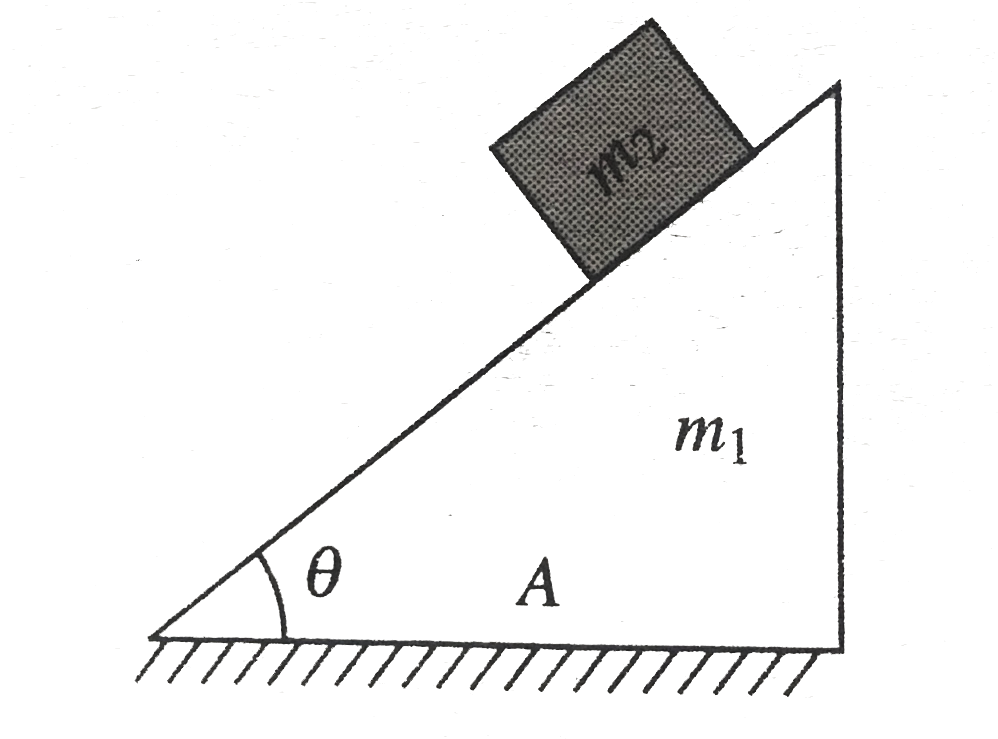
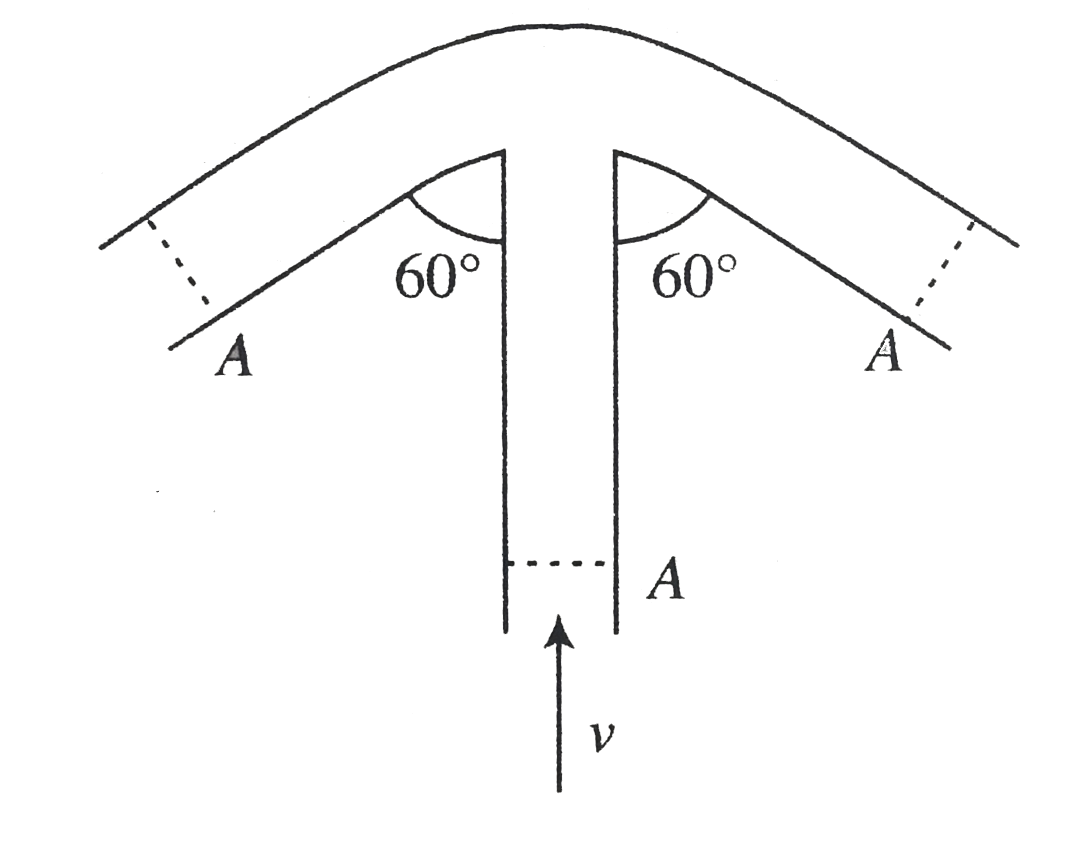
View SolutionIn fig., the mass `m_(2)` starts with velocity `v_(0)` and moves with constant velocity on the surface. During motion, the normal reaction between the horizontal surface and fixed triangle block `m_(1)` is `N`. Then during motion.
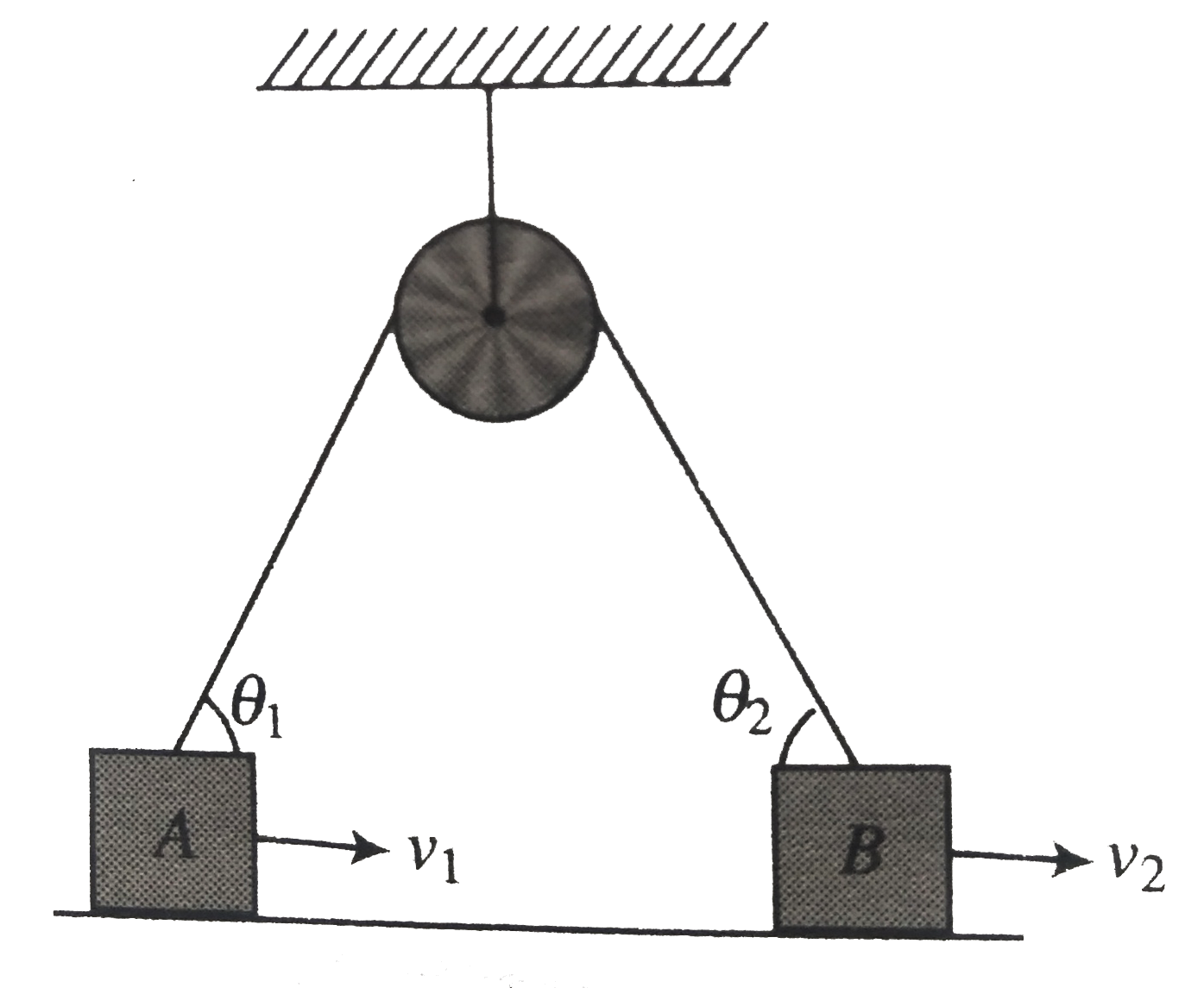
View SolutionIn fig., blocks A and B move with velocities `v_(1)` and `v_(2)` along horizontal direction. Find the ratio of `v_(1)//v_(2)`
View SolutionA rope is strecthed between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has mass of 250kg. Whereas the mass of second boat is double of this mass. If the initial distance between the boats was 100m. The time taken for two boats to meet each other is (neglect water resistance between boats and water)

View SolutionIf block B moves towards right with acceleration b, find the net acceleration of block A.

View SolutionIf the blocks A and B are moving towards each other with accelerations a and b shown in fig. find the net acceleration of block C.

View SolutionA small marble is projected with a velocity of `10 m//s` in a direction `45^(@)`from the y-direction on the smooth inclined plane. Calculate the magnitude `v` of its velocity of after `2 s` (Take `g = 10 m//s^(2))`

View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
View SolutionBlock B has mass m and is released from rest when it is on top of wedge A, which has a mass 3m. Determine the tension in cord CD needed to hold the wedge from moving while B is sliding down A. Neglect friction.

View SolutionA particle of mass 2kg moves with an initial velocity of `vec(v)=4hat(i) +4hat(j) ms^(-1)`. A constant force of `vec(F) =20hat(j)N` is applied on the particle. Initially, the particle was at (0,0). The x-coordinates of the particle when its y-coordinates again becomes zero is given by
View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View SolutionA particle of small m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force on the pulley is
View SolutionAn object is suspended from a spring balance in a lift. The reading is 240 N when the lift is at rest. If the spring balance reading now change to 220N, then the lift is moving
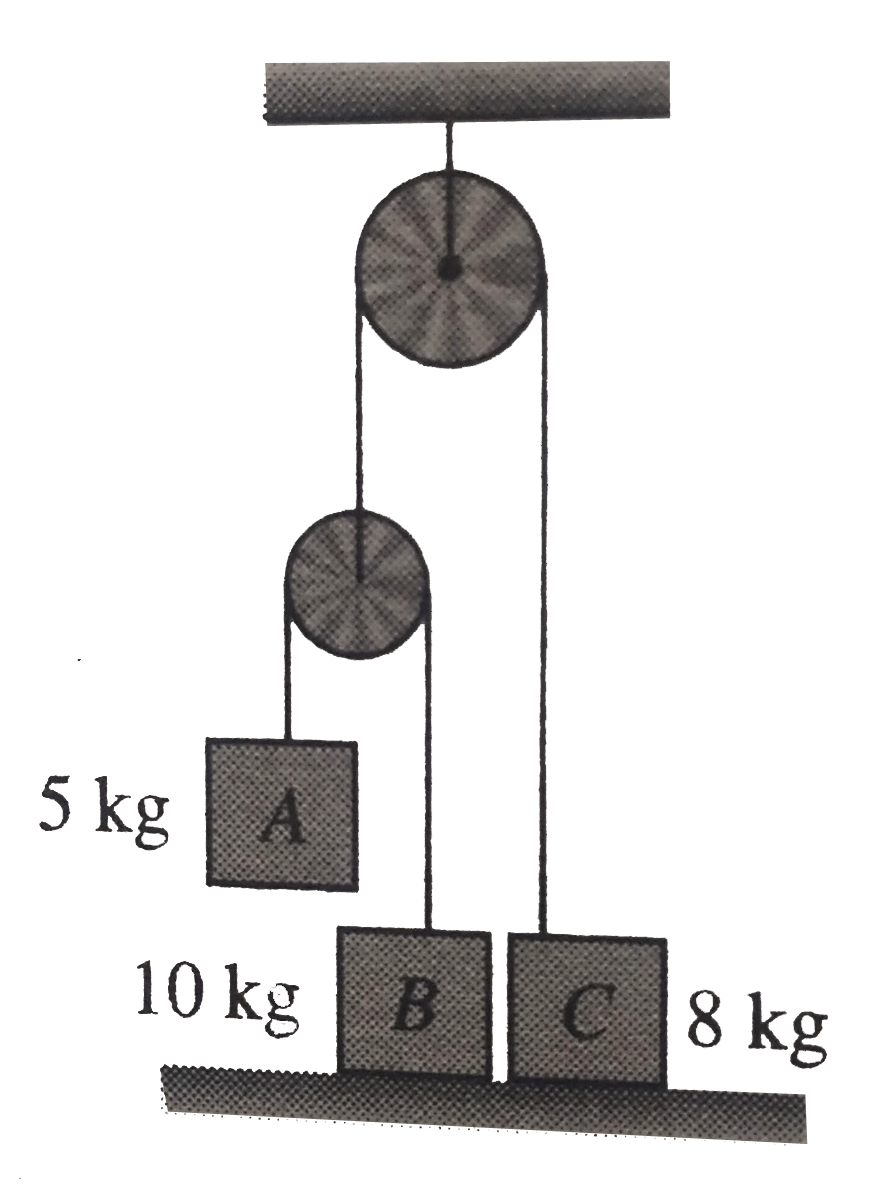
View SolutionIn the following arrangement, the system is initially at rest. The 5-kg block is now released. Assuming the pulley and string to be massless and smooth, the acceleration of block C will be
View SolutionAs shown in fig, if acceleration of M with respect to ground is `2ms^(-2)`, then
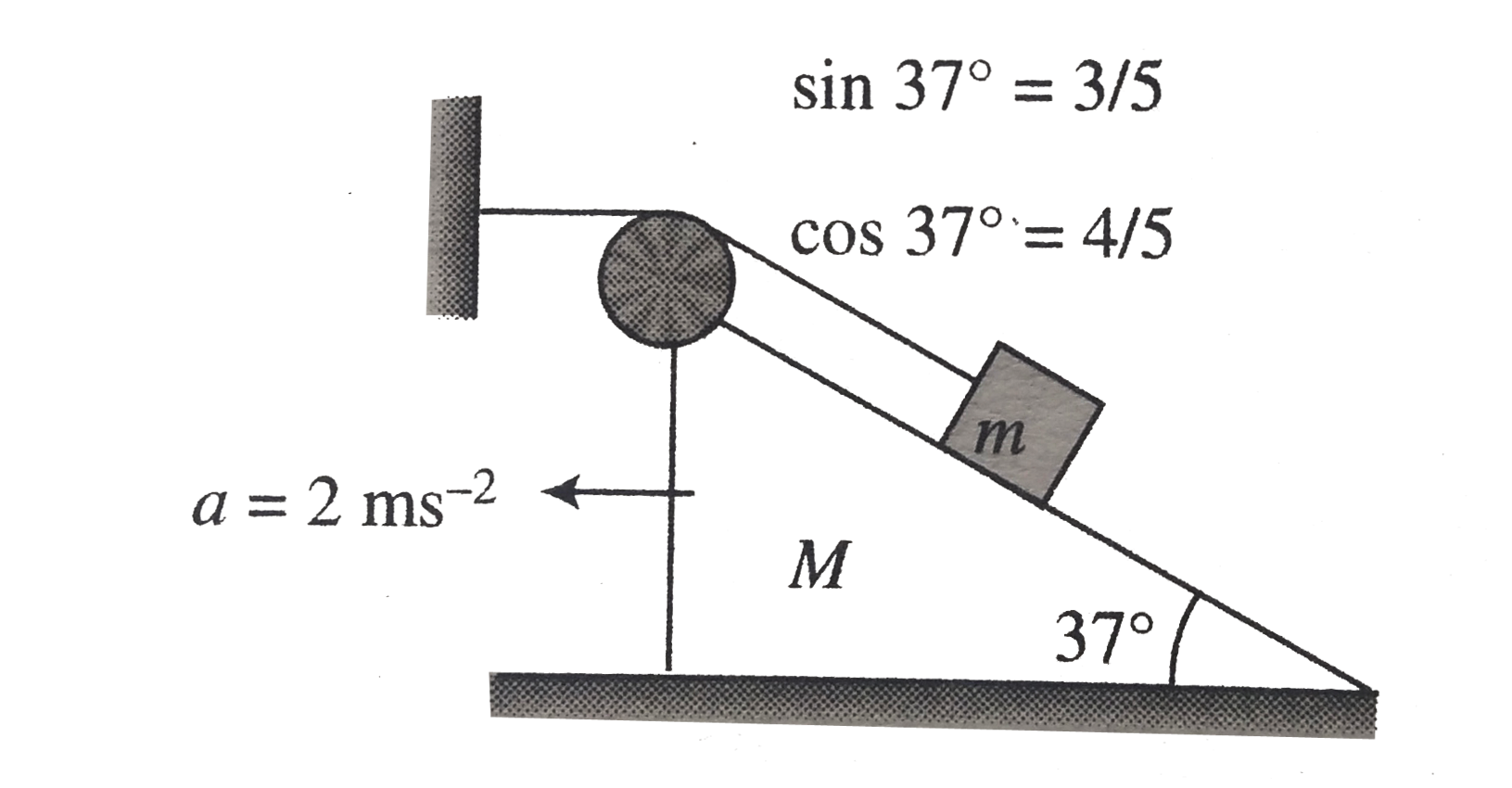
View SolutionA block A has a velocity of `0.6ms^(-1)` the right. Determine the velocity of cylinder B.

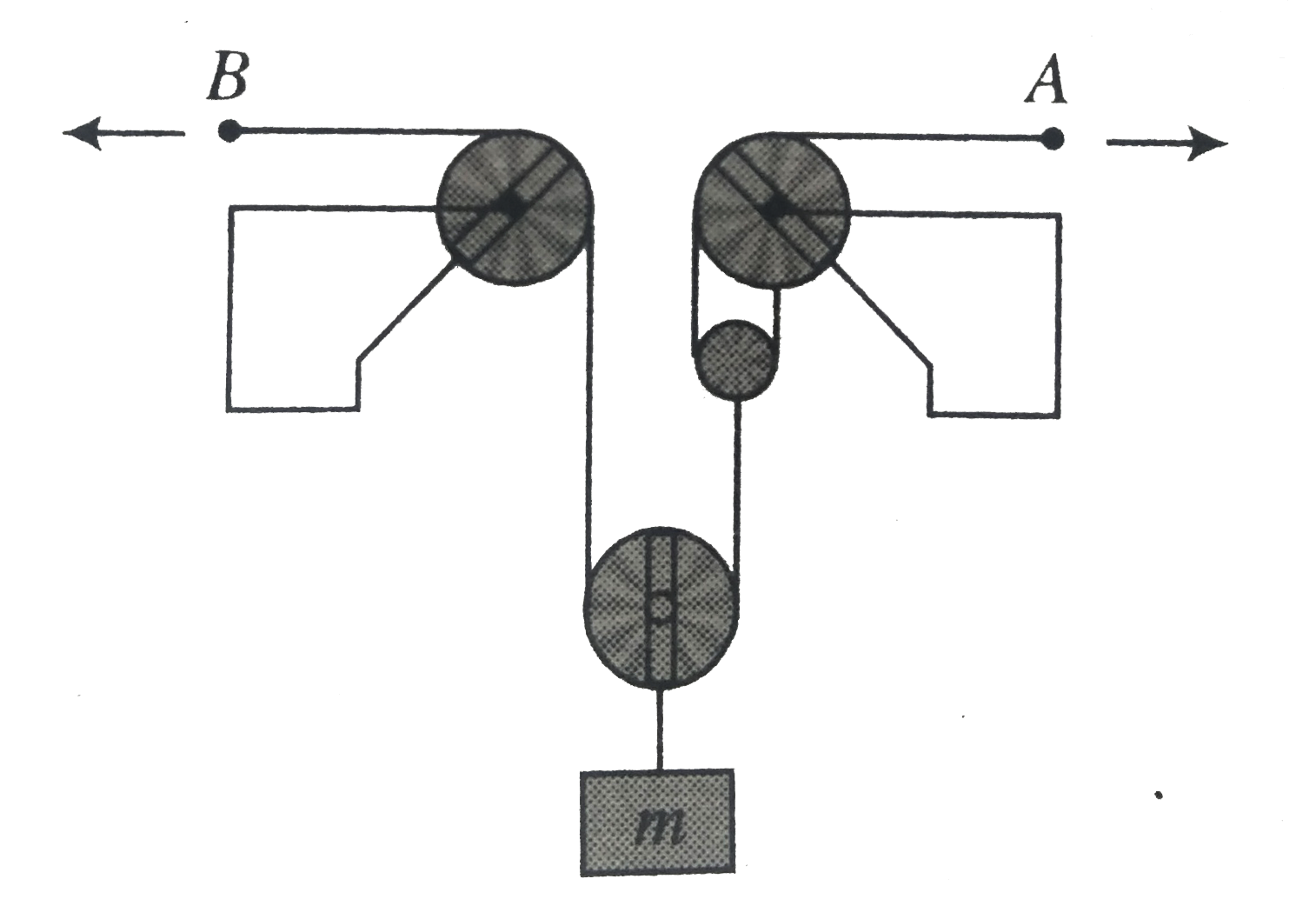
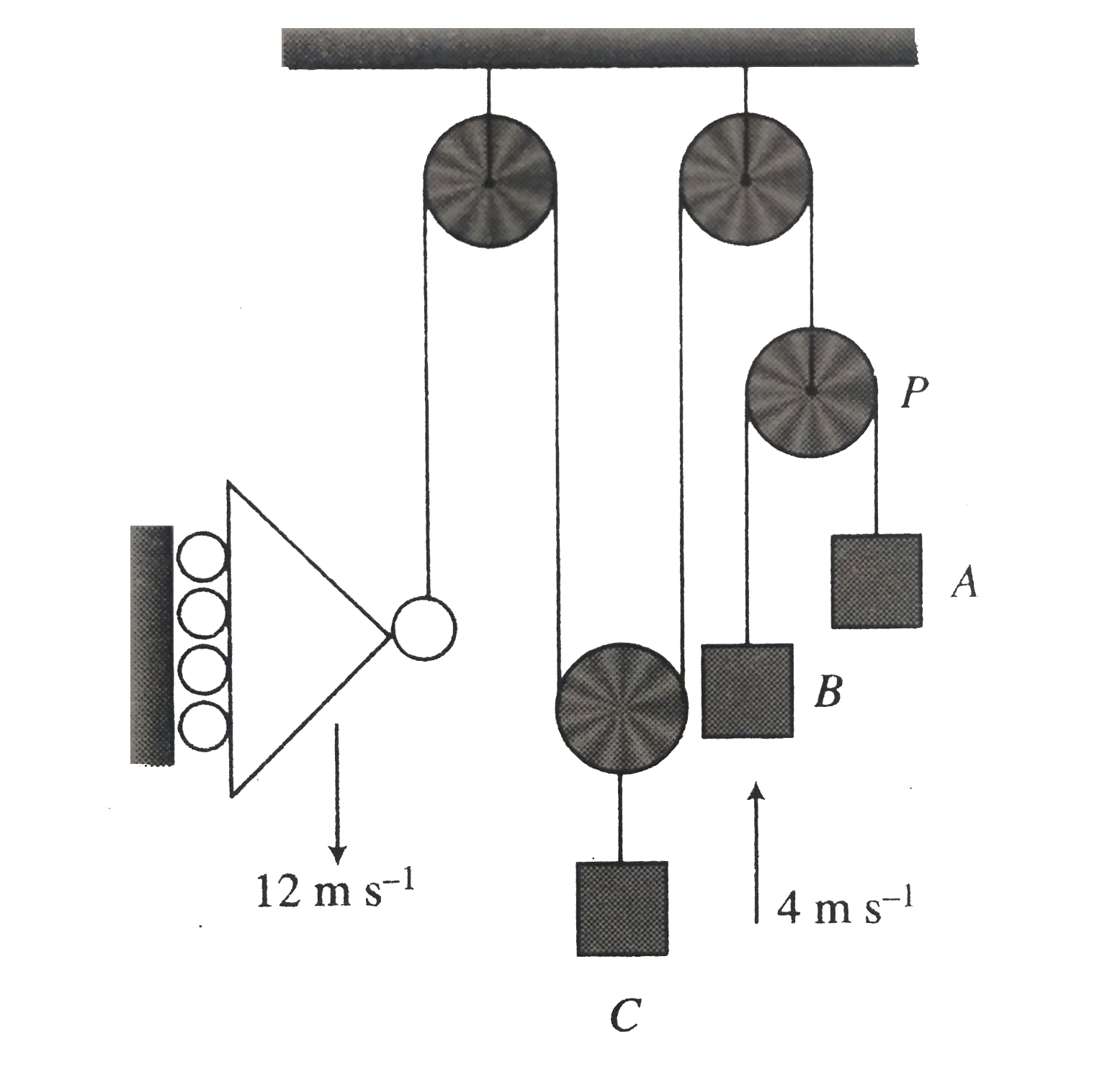
View SolutionFor the pulley system shown in fig. each of the cables at A and B is given a velocity of `2ms^(-1)` in the direction of the arrow. Determine the upward velocity v of the load m.
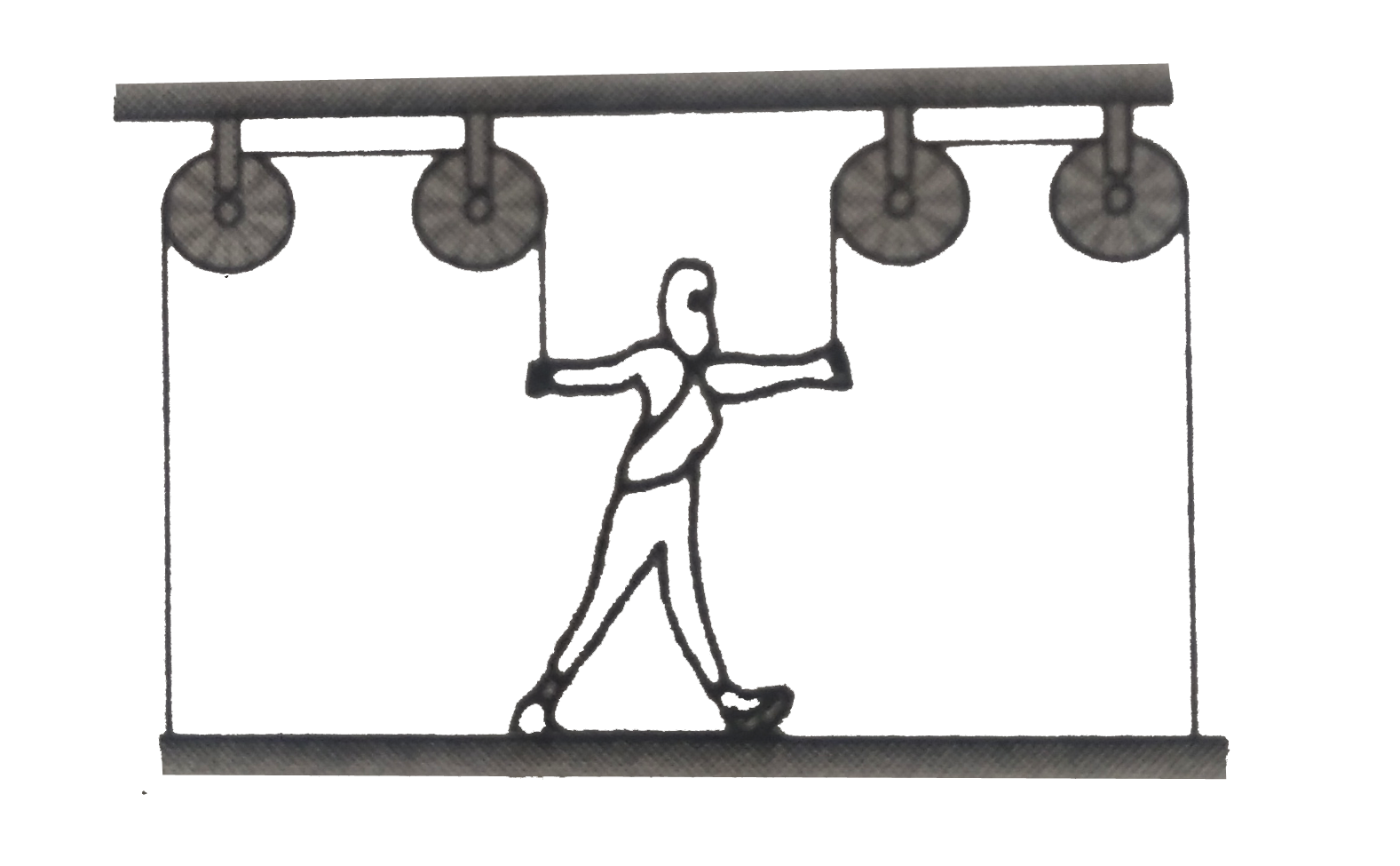
View SolutionA man pulls himself up the `30^(@)` incline by the method shown in fig. if the combined mass of the man and cart is 100kg, determine the acceleration of the cart if the man exerts a pull of 250N on the rope. Neglect all friction and the mass of rope , pulleys and wheels.

View SolutionA painter of mass M stands on a platform of mass m and pulls himself up by two ropes which hang over pulley as shown in fig. He pulls each rope with force F and moves upward with a uniform acceleration a. find a, neglecting the fact that no one could do this for long time.
View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View SolutionA 60kg man stands on a spring scales in a lift. At some instant. He finds that the scale reading has changed from 60kg to 50 kg for a while and then comes back to original mark. What should be concluded?
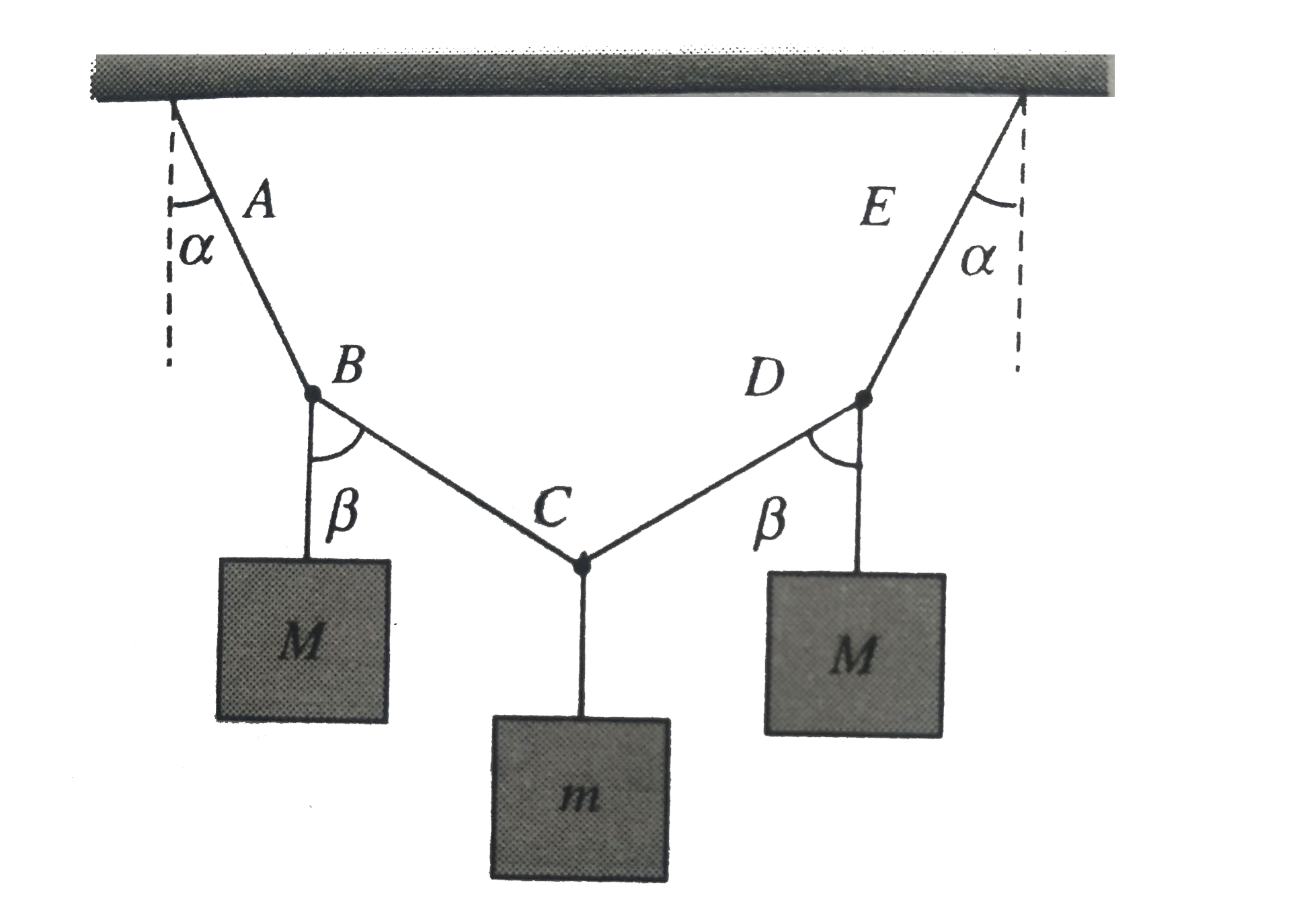
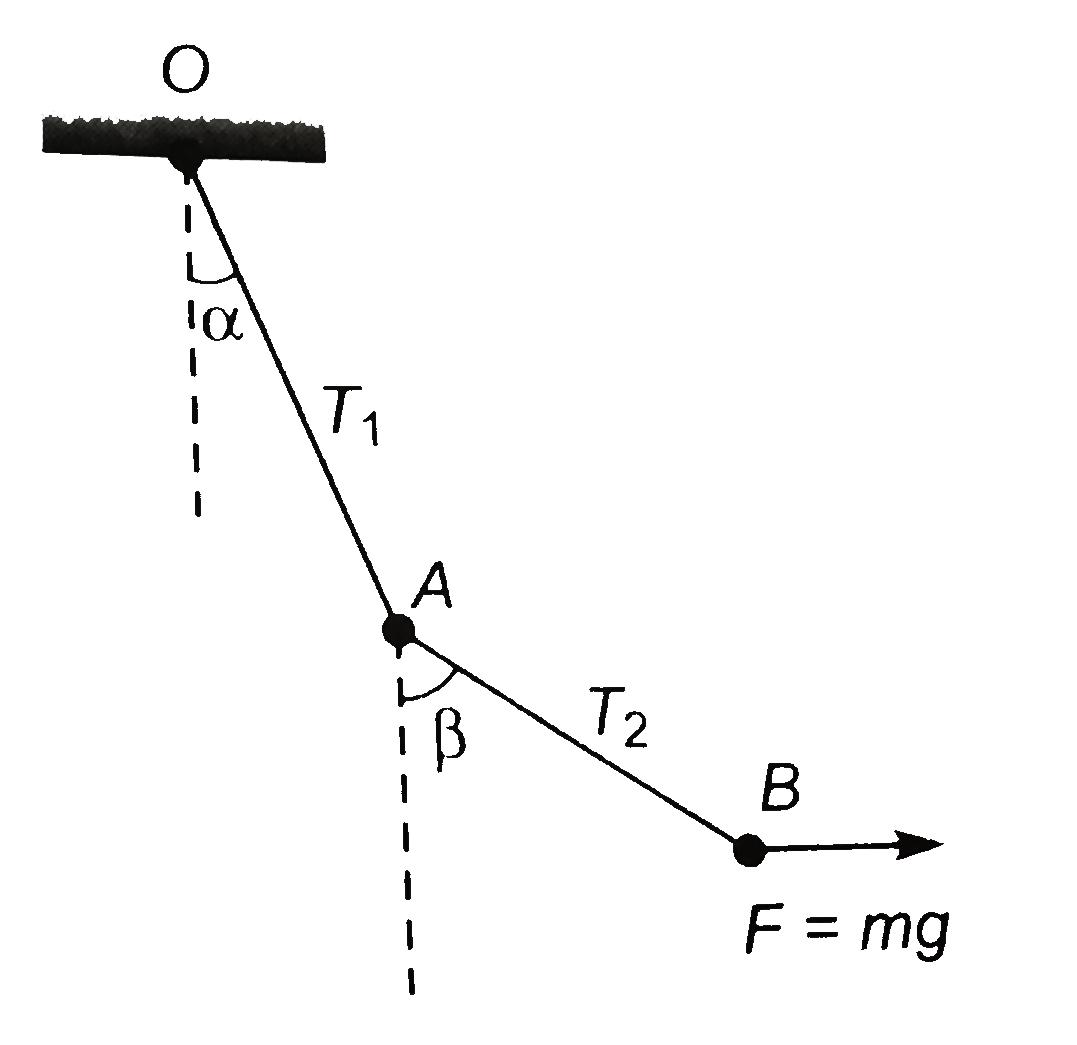
View SolutionFigure, represents a light inextensible string ABCDE in which `AB=BC=CD=DE` and to which are attached masses M,m, and M at the point B,C and D, respectively. The system hangs freely in equilibrium with ends A and E of the string fixed in the same horizontal line. it is given that `tan alpha=3//4` and `tan beta=12//5`. Then the tension in the string BC is
View SolutionIf block A is moving with an acceleration of `5ms^(-2)`, the acceleration of B w.r.t. ground is

View SolutionTwo particles `A` and `B` each of mass `m` are kept stationary by applying a horizontal force `F = mg` on particle `B` as show in figure .Then
View SolutionA block of metal weighing 2kg is resting on a frictionless plane. It is struck by a jet releasing water at a rate of `1kg s^(-1)` and at a speed of `5ms^(_1)`. The initial acceleration of the block is

View SolutionAn ideal liquid of density `rho` is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.
View SolutionTwo uniform solid cylinders A and B each of mass 1 kg are connected by a spring of constant `200Nm^(-1)` at their axles and are placed on a fixed wedge as shown in fig.There is no friction between cylinders and wedge. The angle made by the line AB with the horizontal, in equilibirum is

View SolutionThe velocity of point A on the rod is `2ms^(-1)` (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
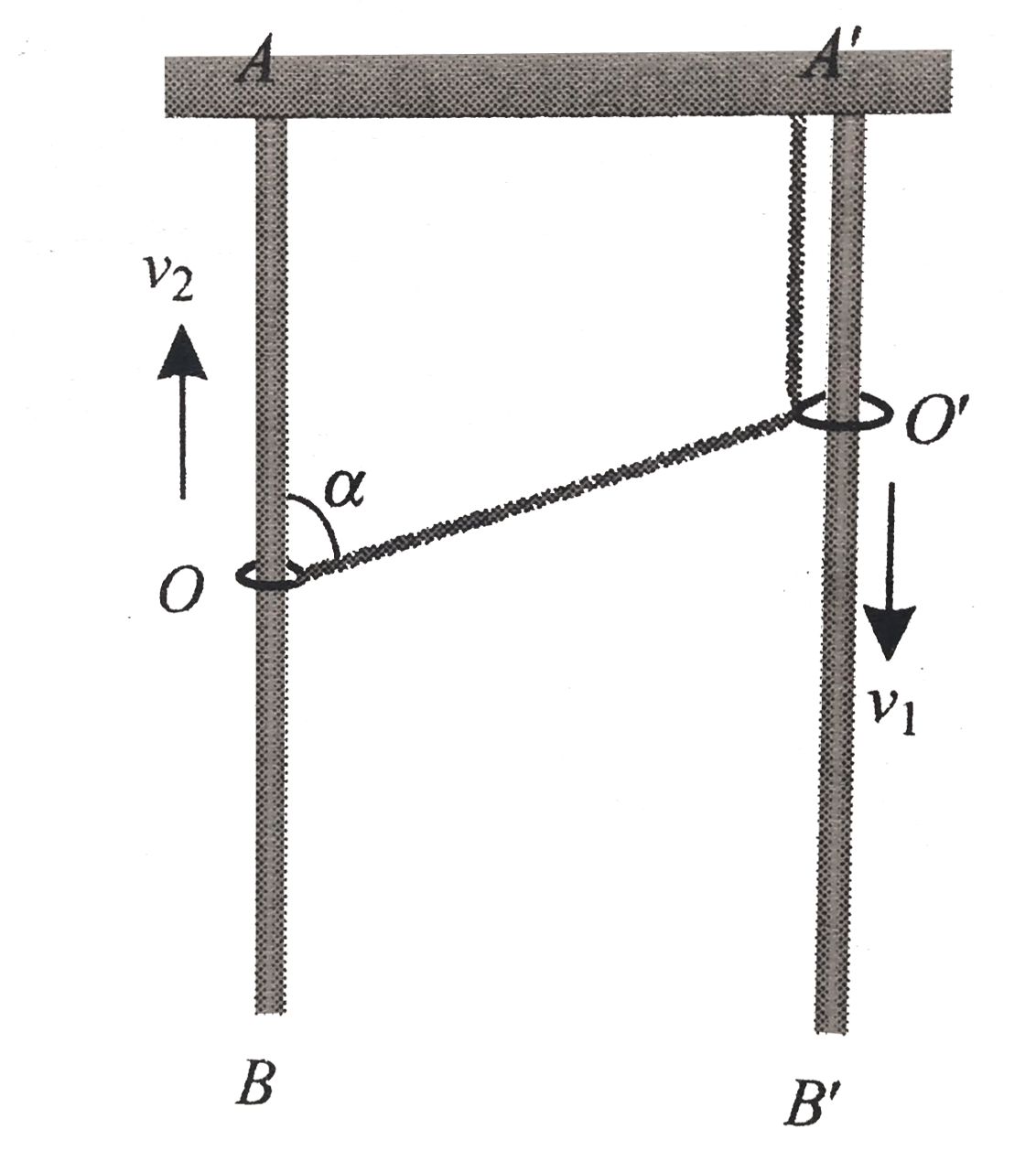
View SolutionTwo small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring `O'` and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity `v_(1)`, then velocity `v_(2)` of the ring O, when `/_AOO'=alpha` is
View SolutionA U-shaped smooth wire has a semi-circular bending between A and B as shown in fig. A bead of mass m moving with uniform speed v through the wire enters the semiculcular bent at A and leaves at B. Find the average force exerted by the bead on the part AB of the wire.

View SolutionTwo identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

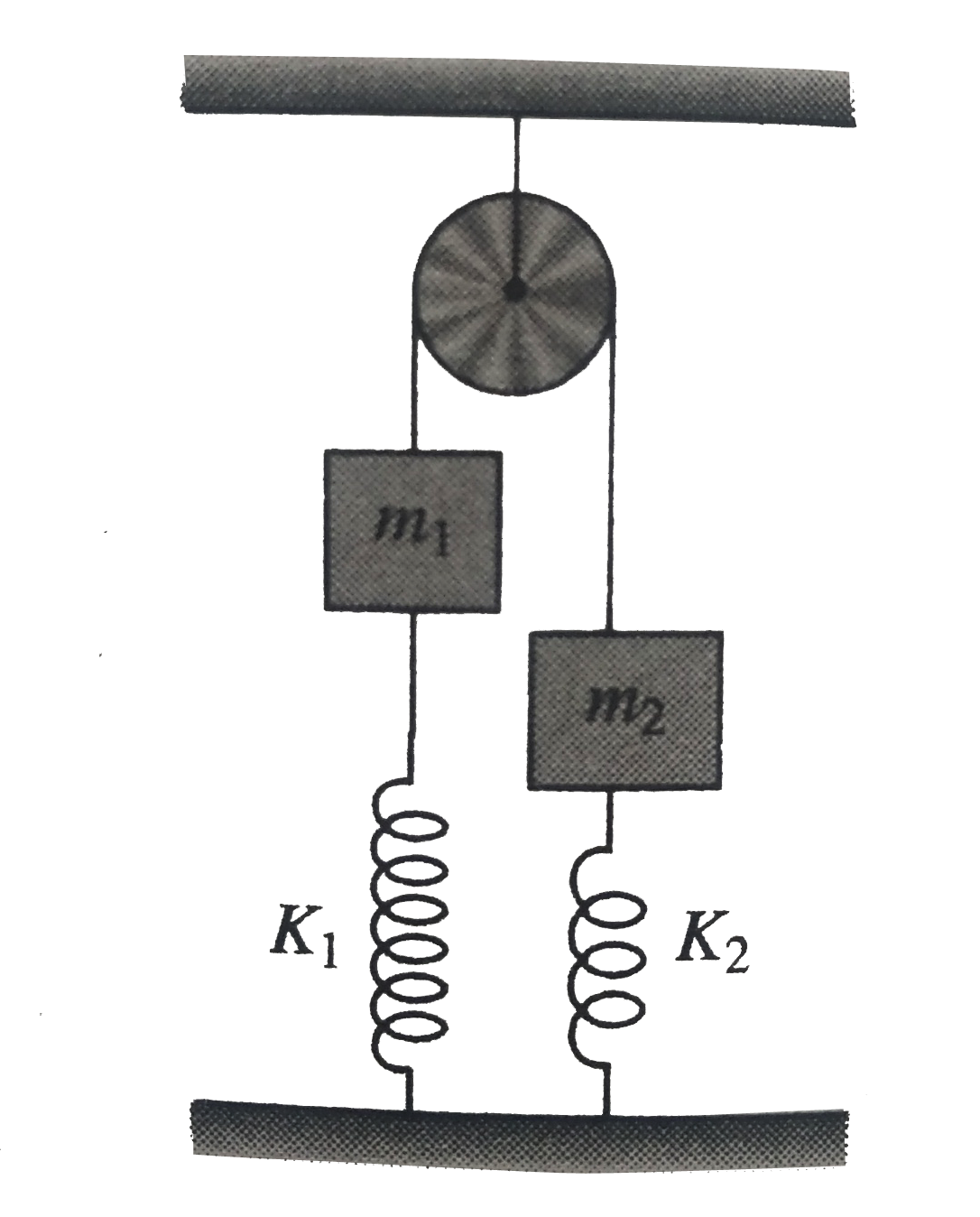
View SolutionThe system shown in fig is in equilibrium . Masses `m_(1) and m_(2)` are 2kg and 8kg, Respectively. Spring constants `k_(1) and k_(2)` are `50Nm^(-1) and 70Nm^(-1)`, respectively. If the compression in second spring is 0.5m. What is the compression in first spring?
View SolutionIn fig. the block of mass M is at rest on the floor . At what acceleration with which should a boy of mass m climb along the rope of negligible mass so as to lift the block from the floor?
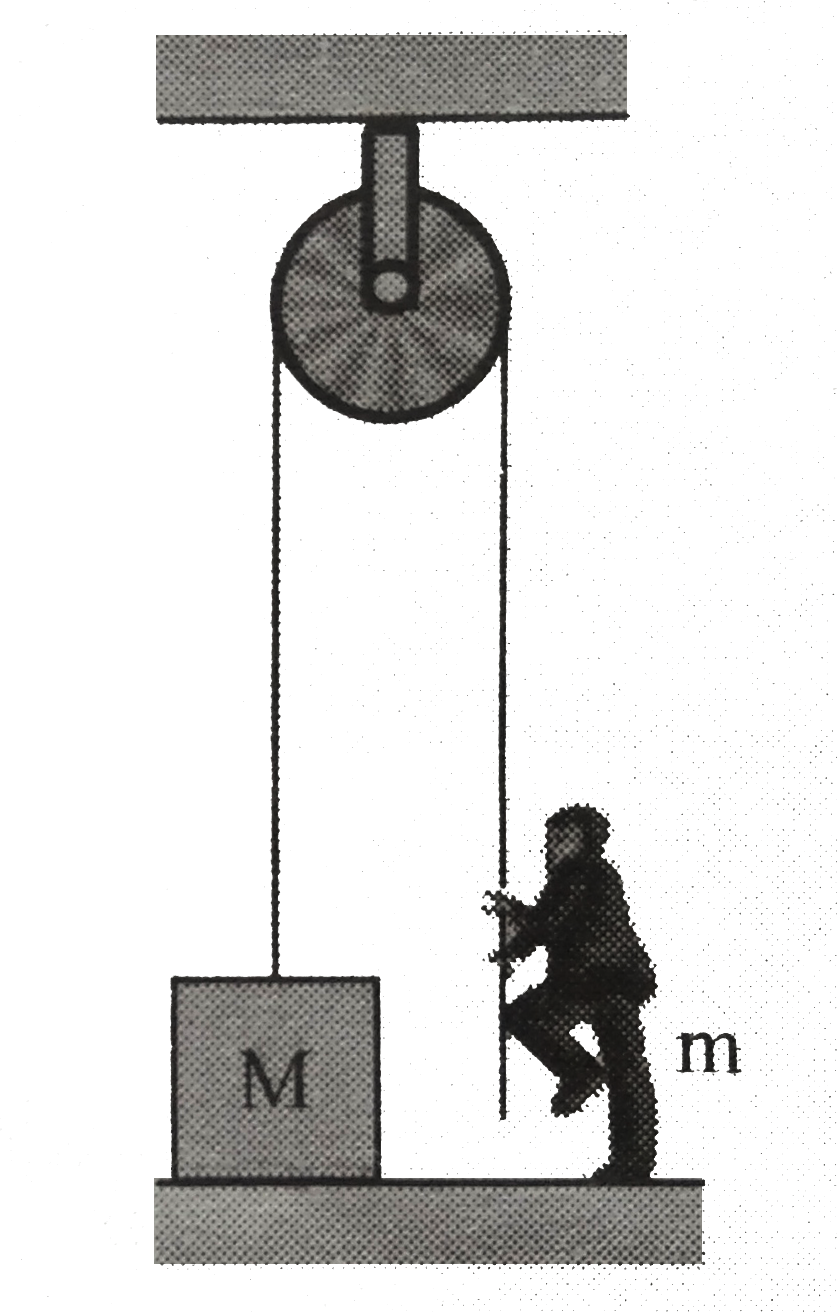
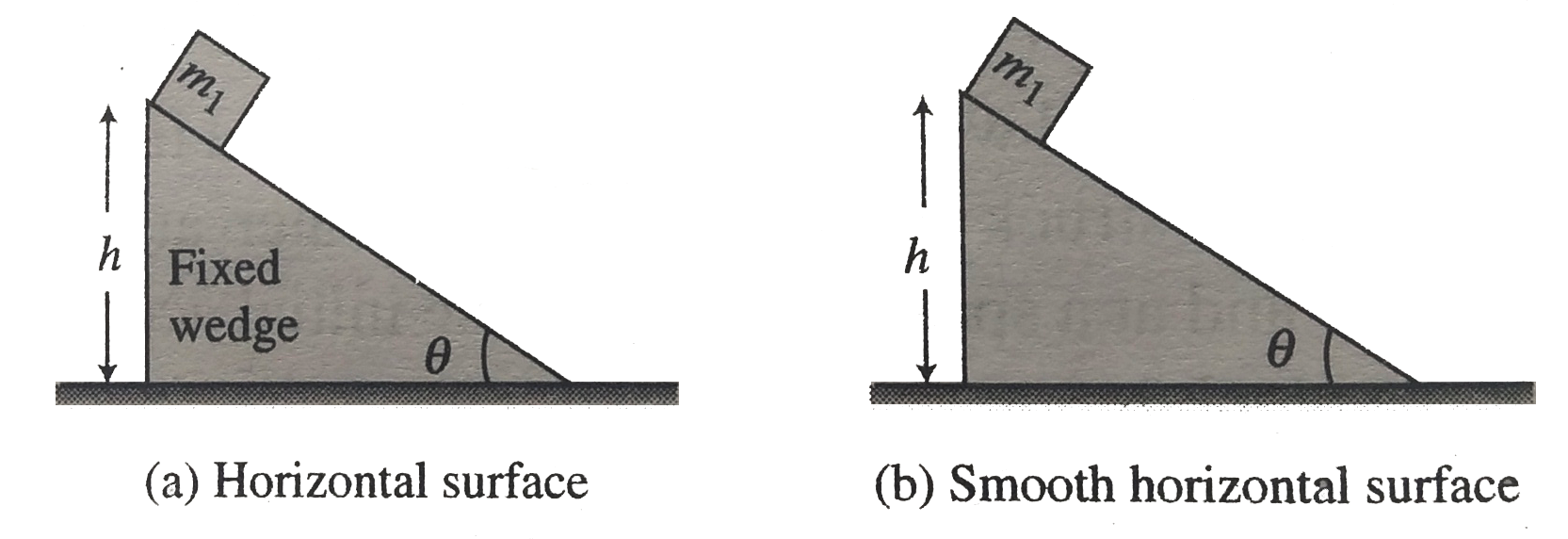
View SolutionA block of mass `m_(1)` lies on the top of fixed wedge as shown in fig. and another block of mass `m_(2)` lies on top of wedge which is free to move as shown in fig. At time t=0 both the blocks are released from rest from a vertical height h above the respective horizontal surface on which the wedge is placed as shown. There is no friction between block and wedge in both the figures. Let `T_(1)` and `T_(2)` be the time taken by the blocks respectively to just reach the horizontal surface. then
View SolutionIn the situation shown in fig., all the strings are light and inextensible and pullies are light. There is no friction at any surface and all blocks are of cuboidal shape. A horizontal force of magnitude F si applied to right most free end of string in both cases shown in the figure. At the instant shown, the tension in all strings are non-zero. Let the magnitudes of acceleration of large blocks (of mass M) in fig. be `a_(1) and a_(2)` respectively. Then,

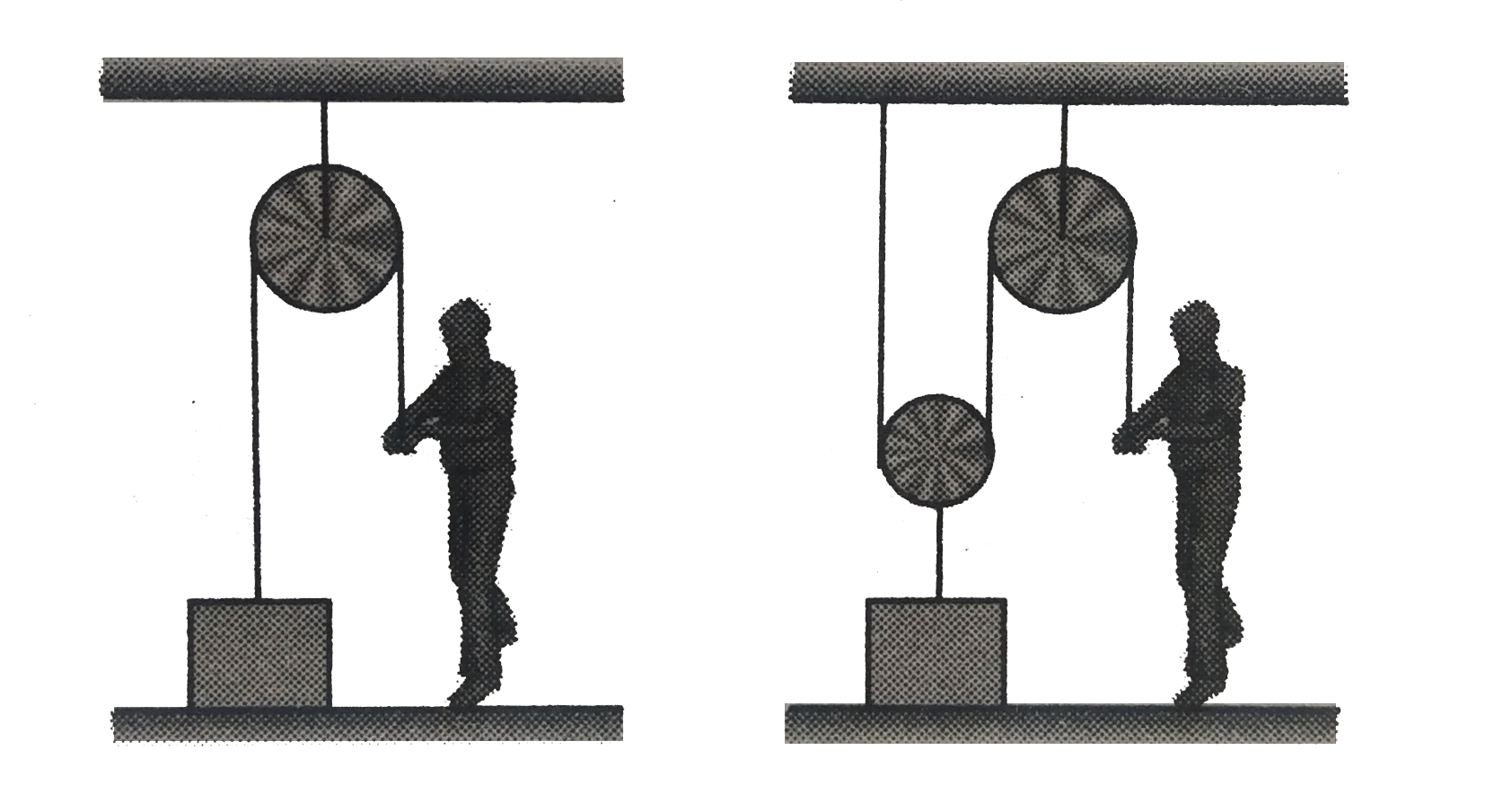
View SolutionIn fig., a person wants to rise a block lying on the ground to a height h. In both the cases, if the time required is same, then in which case he has to exert more force? Assuem pulleys and strigns light.
View SolutionA wooden box is placed on a table. The normal force on the box from the table is `N_(1)`. Now another identical box is kept on first box and the normal force on lower block due to upper block is `N_(2)` and normal force on lower block by the table is `N_(3)`. For this situtation, mark out the correct statement (s).
View SolutionIn the arrangement shown in fig., if the acceleration of B is `vec(a)`. Then find the acceleration of A.

View SolutionIf the acceleration of wedge in the shown arrangement is a `ms^(-2)` towards left, then at this instant, acceleration of the block (magnitude only) would be
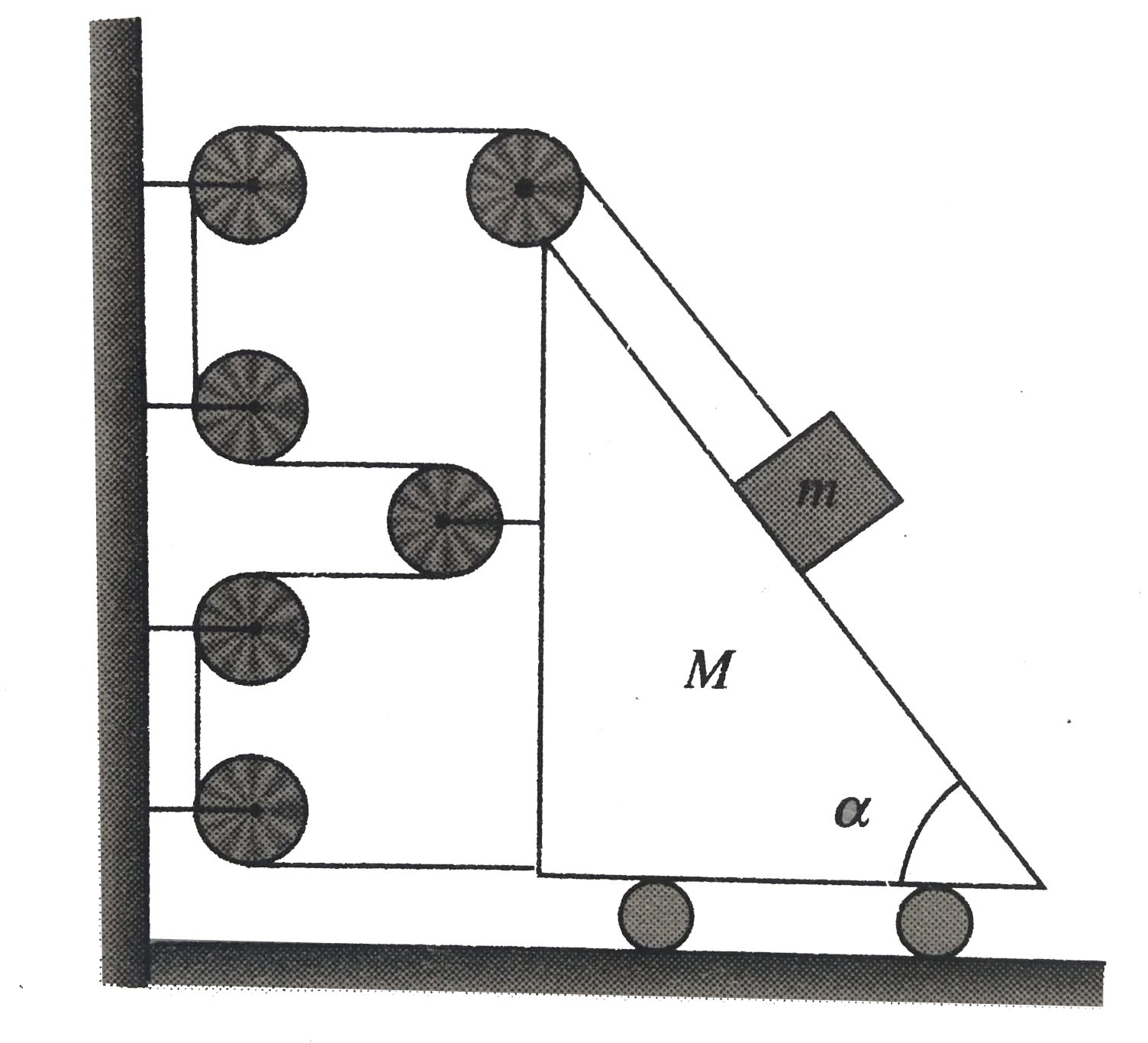
View SolutionIn the arrangement shown in fig., at a particular instant, the roller is coming down with a speed of `12ms^(-1)` and C is moving up with `4ms^(-1)`. At the same instant, it is also known that w.r.t. pulley P, block A is moving down with speed `3ms^(-1)` . Determine the motion of block B (velocity ) w.r.t. ground.
View SolutionA particle of mass 2kg moves with an initial velocity of `(4hat(i)+2hat(j))ms^(-1)` on the x-y plane. A force `vec(F)=(2hat(i)-8hat(j))N` acts on the particle. The initial position of the particle is (2m,3m). Then for `y=3m`,
View SolutionFigure shows the variation of force acting on a boby with time. Assume the body to start from rest, the variation of its momentum with time is best represented by which plot?
View SolutionFor the system shown in fog. `m_(1) gt m_(2) gtm_(3) gt m_(4)`. Initially, the system is at rest in equilibrium condition., if the string joining `m_(4)` and ground is cut, then just after the string is cut.
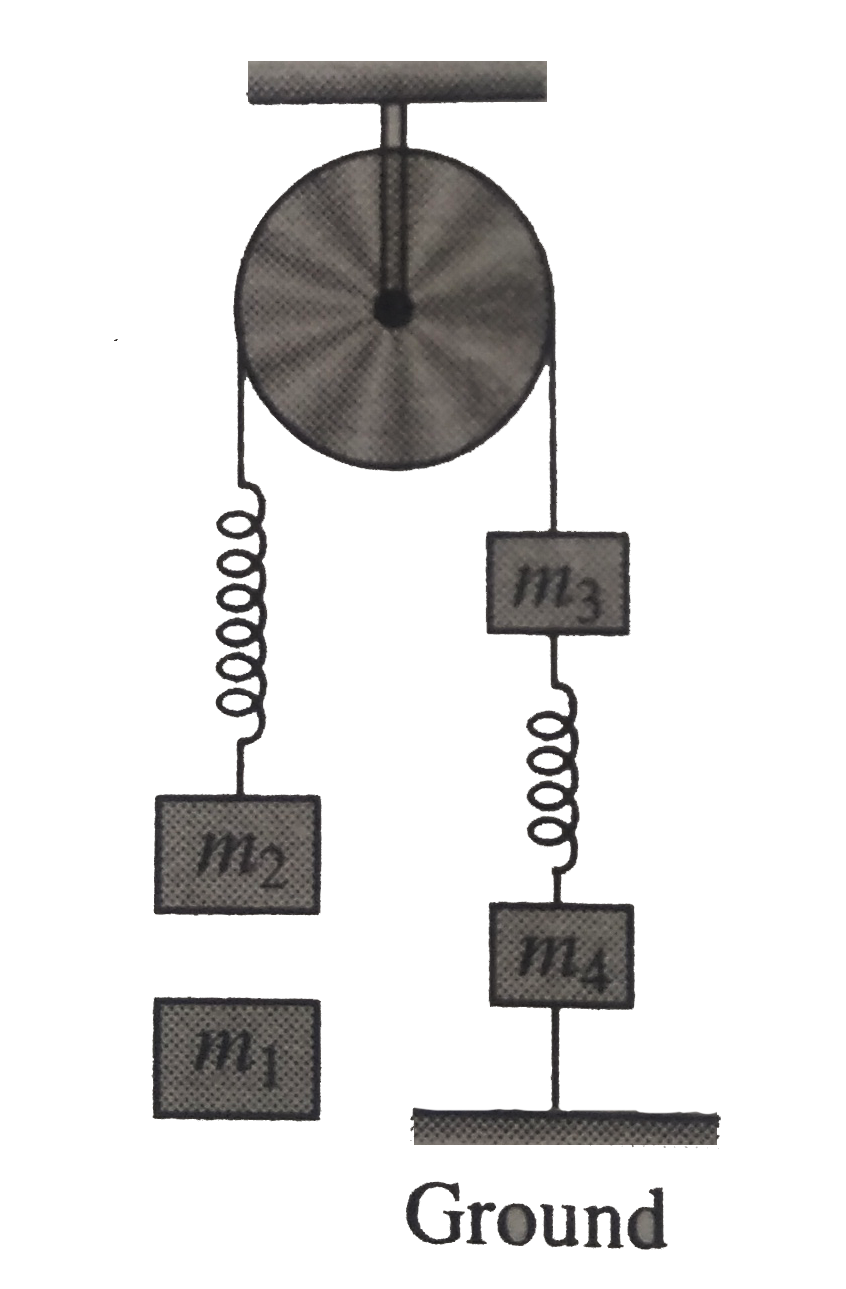
Statement I: `m_(1), m_(2), m_(3)` remain stationary.
Statement II: The value of acceleration of all the four blocks can be determined.
Statement III: Only `m_(4)` remain stationary.
Statement IV: Only `m_(4)` accelerates.
View SolutionA particle is moving in the x-y plane. At certain instant of time, the components of its velocity and acceleration are as follows: `v_(x)=3ms^(-1), v_(y)=4ms^(-1), a_(x)=2ms^(-2) and a_(y)=1ms^(-2)`. The rate of change of speed at this moment is
View SolutionFigure shows two blocks each of mass m system is released from rest. If acceleration of blocks A and B at any instant (not initially) are `a_(1)` and `a_(2)`, respectively. Then
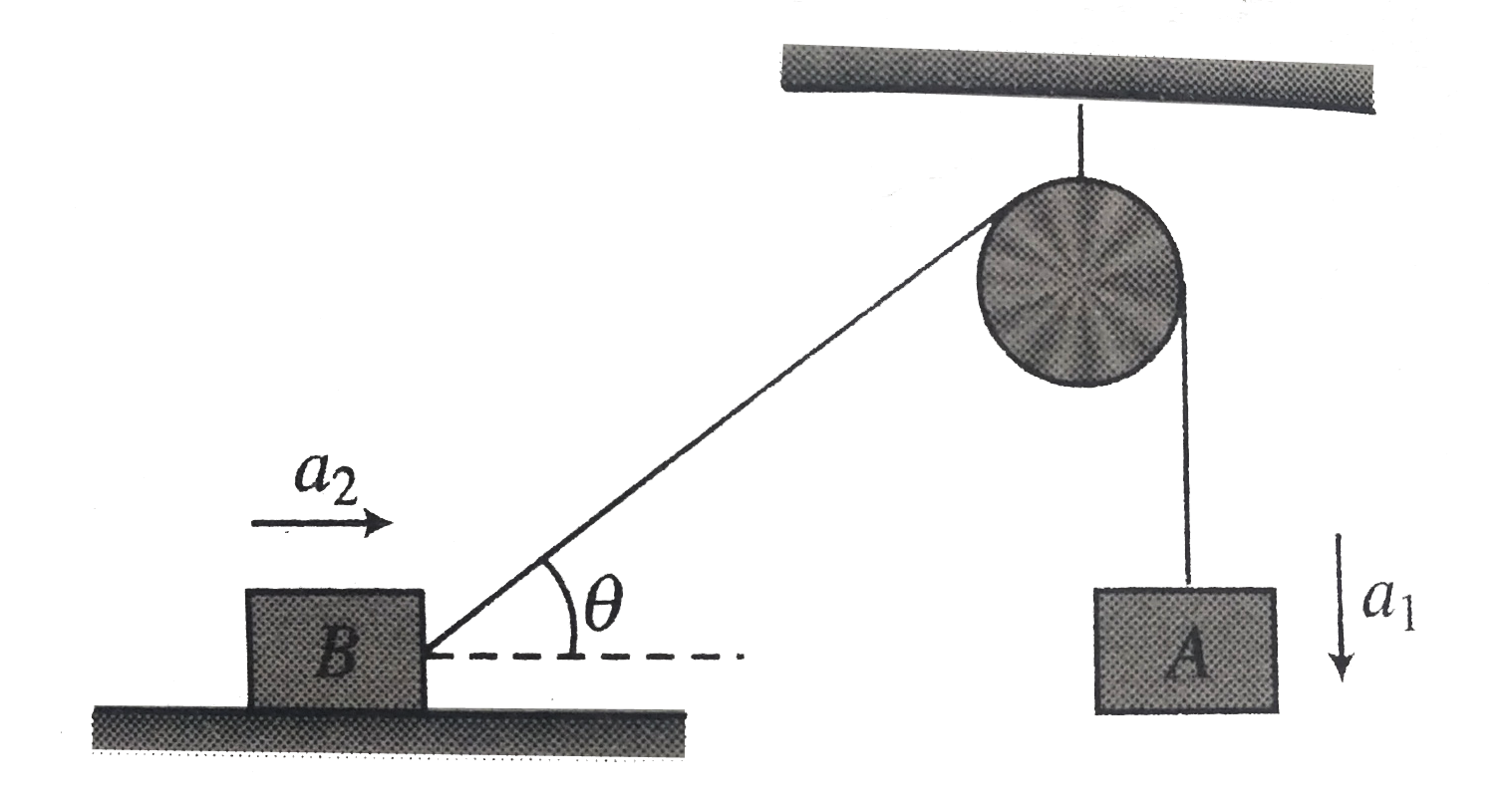
View SolutionIf block A is moving horizontally with velocity `v_(A)`, then find the velocity of block B at the instant as shown in fig.
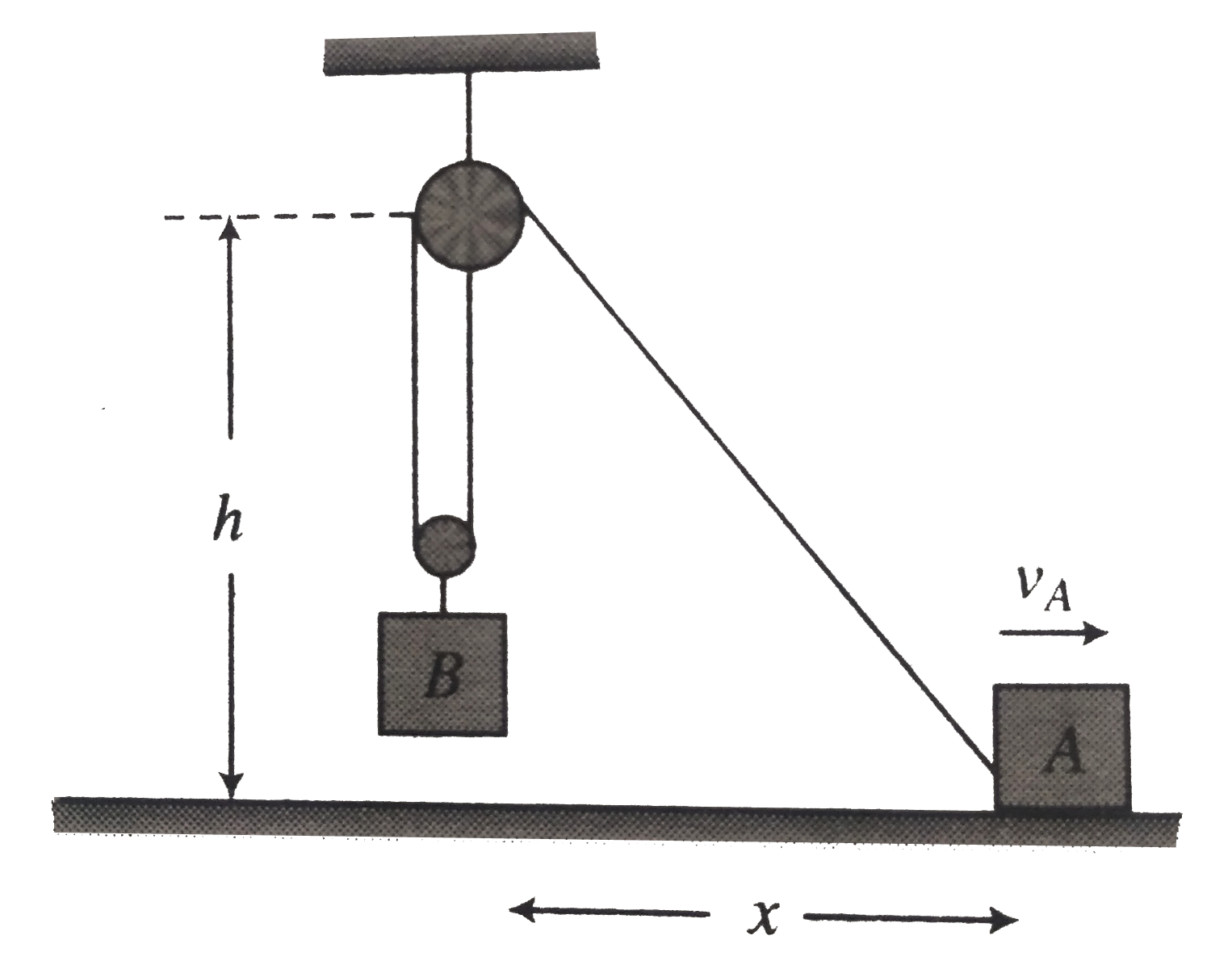
View SolutionA small block of mass m rests on a smooth wedge of angle `theta`. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?
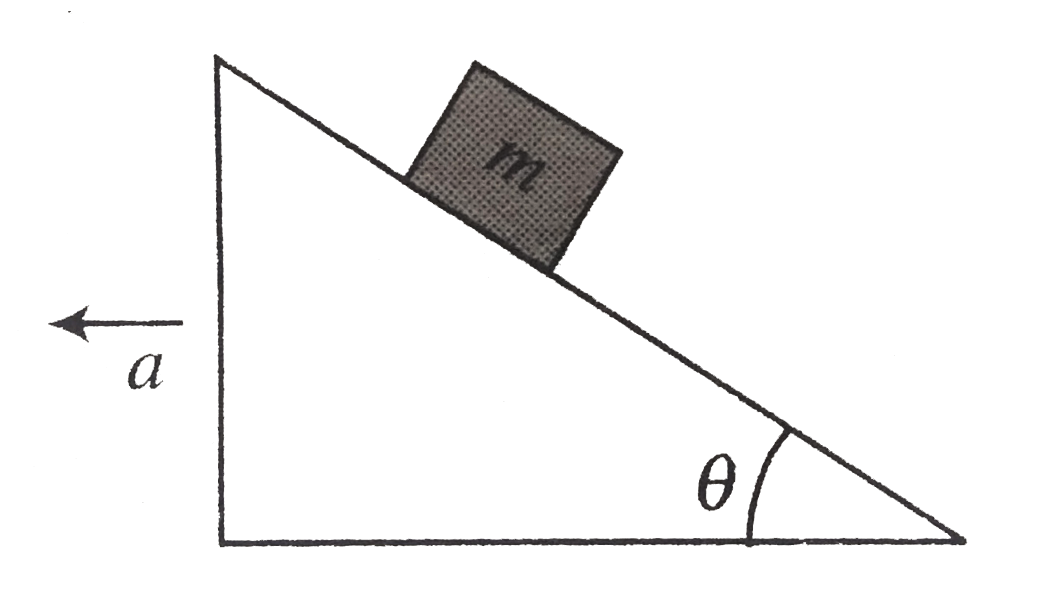
View SolutionIn fig. man A is standing on a movable plank while man B is standing on a stationary platform. Both are pulling the string down such that the plank moves slowly up. As a result of this the string slops through the hands of the men, find the ratio of length of the string that slips through the hands of A and B.

View SolutionTwo trolley 1 and 2 are moving with acceleration `a_(1)` and `a_(2)` respectively, in the same direction. A block of mass m on trolley 1 is in equilibrium from the frame of observer stationary with respect to trolley 2. the magnitude of friction force on block due to trolley is (assume that no horizontal force other than friction force is acting on block).
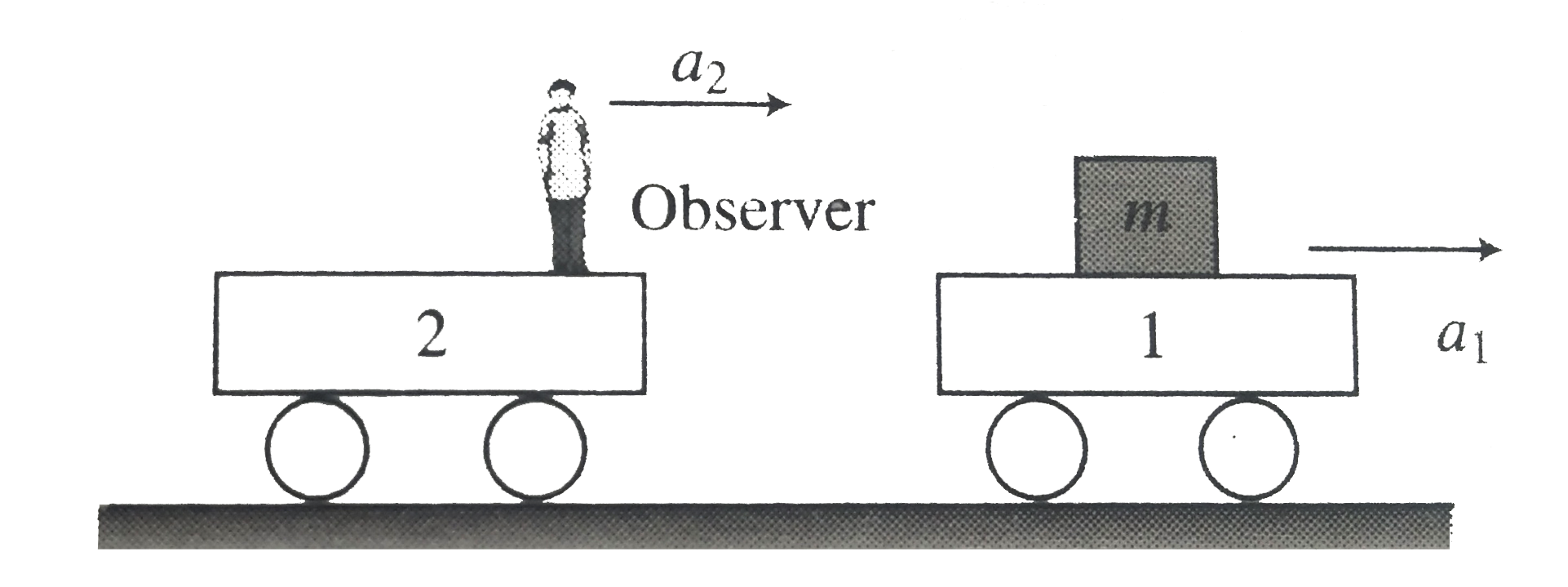
View SolutionIn the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is

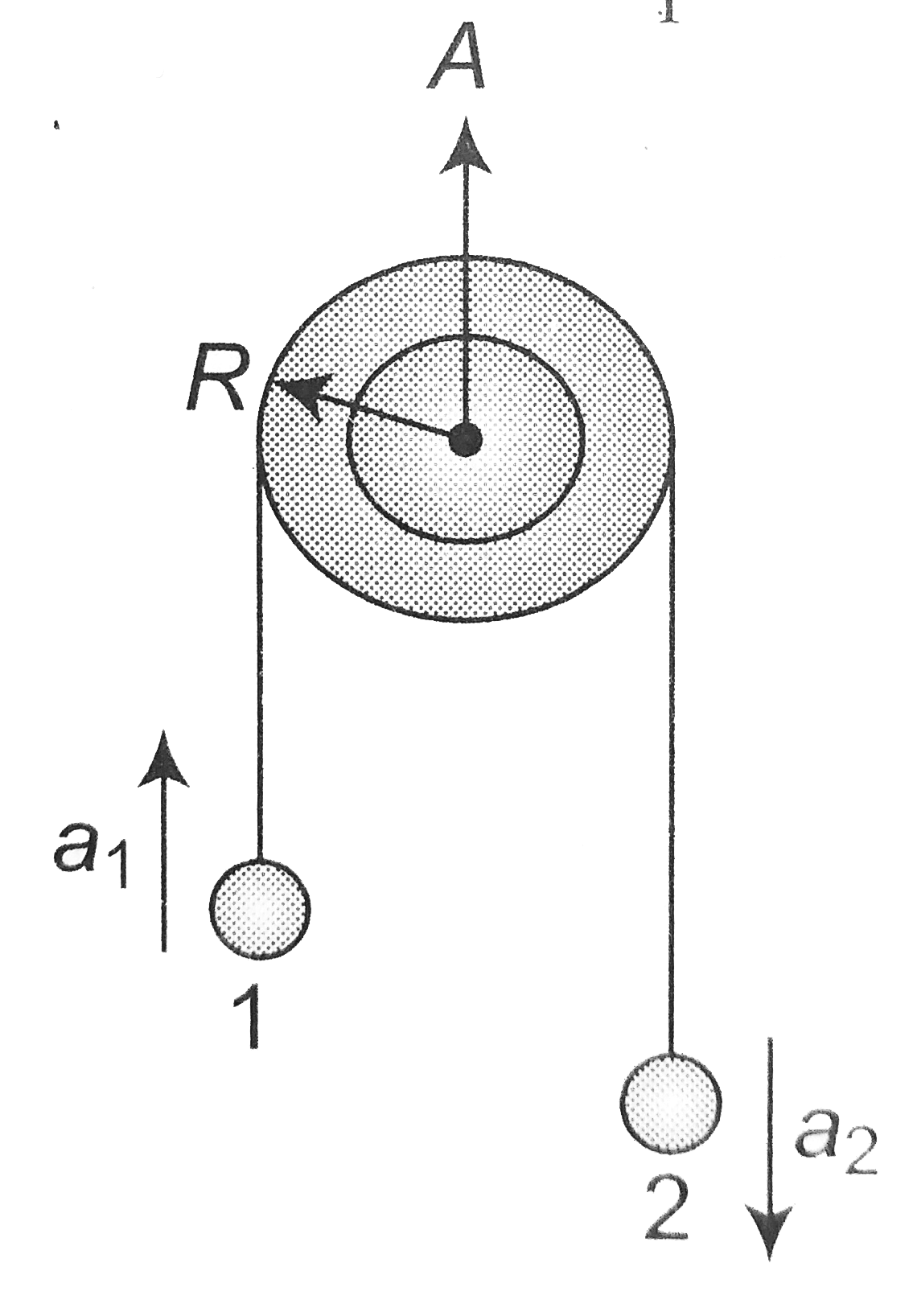
View SolutionTwo masses are connected by a string which passes over a pulley acceleration upward at a rate `A` shown. If `a_(1)` and `a_(2)` be the accelerations of bodies 1 and 2 respectively then,
View SolutionIn fig, the acceleration of A is `vec(a)_(A)=15hat(i)+15hat(j)`. Then the acceleration of B is (A remains in constact with B)
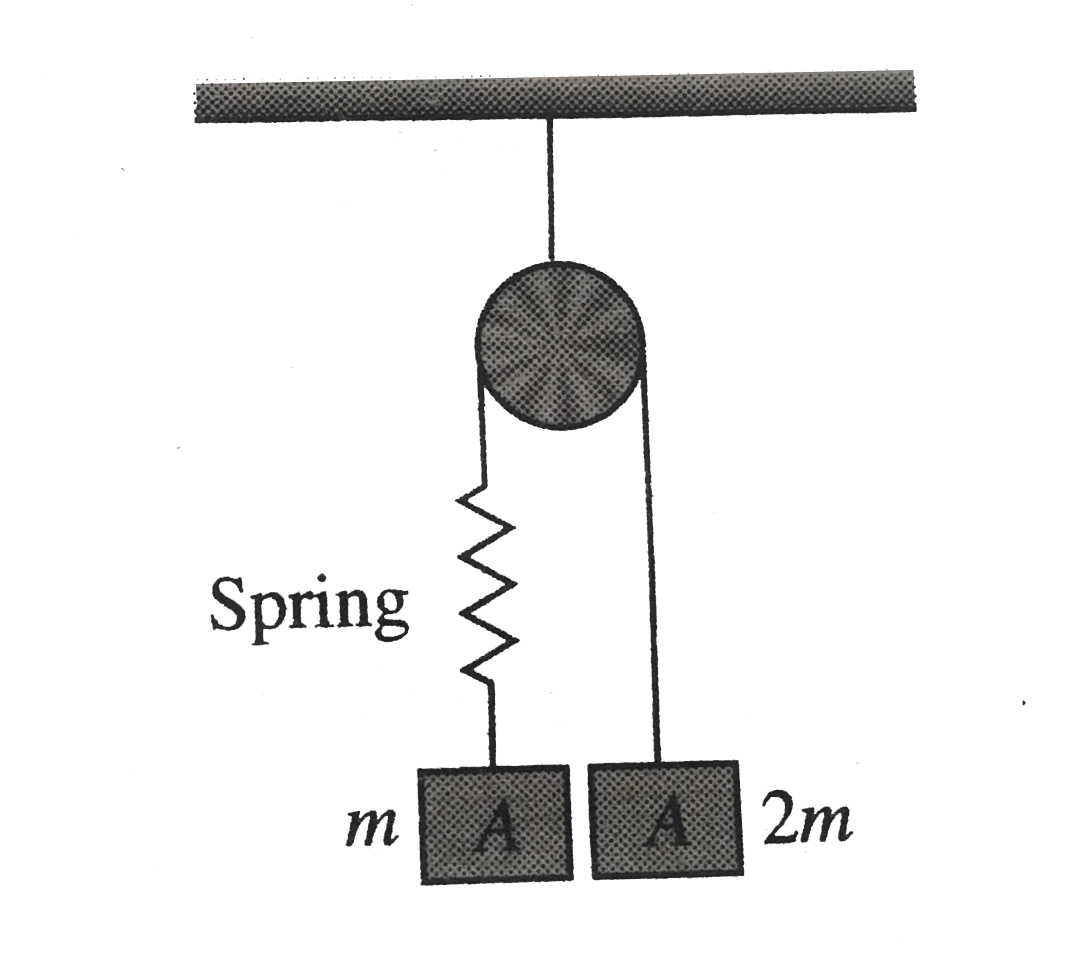
View SolutionTwo blocks A and B of masses m and 2m, respectively , are held at rest such that the spring is in natural length. Find out the acceleration of both the blocks just after relese.
View SolutionA bob is hanging over a pulley inside a car through a string. The second end of the string is in the hands of a person standing in the car. The car is moving with constant acceleration a directed horizontally as shown in fig. The other end of the string is pulled with constant acceleration a vertically. The tension in the string is equal to

View SolutionInside a horizontal moving box, an experimenter finds that when an object is placed on a smooth horizontal table and is released, it moves with an acceleration of `10ms^(-2)`, in this box. If 1-kg body is suspended with a light string. The tension in the string in equilibrium position. (w.r.t. experimenter) will be (take `g=10ms^(-2)`)
View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)
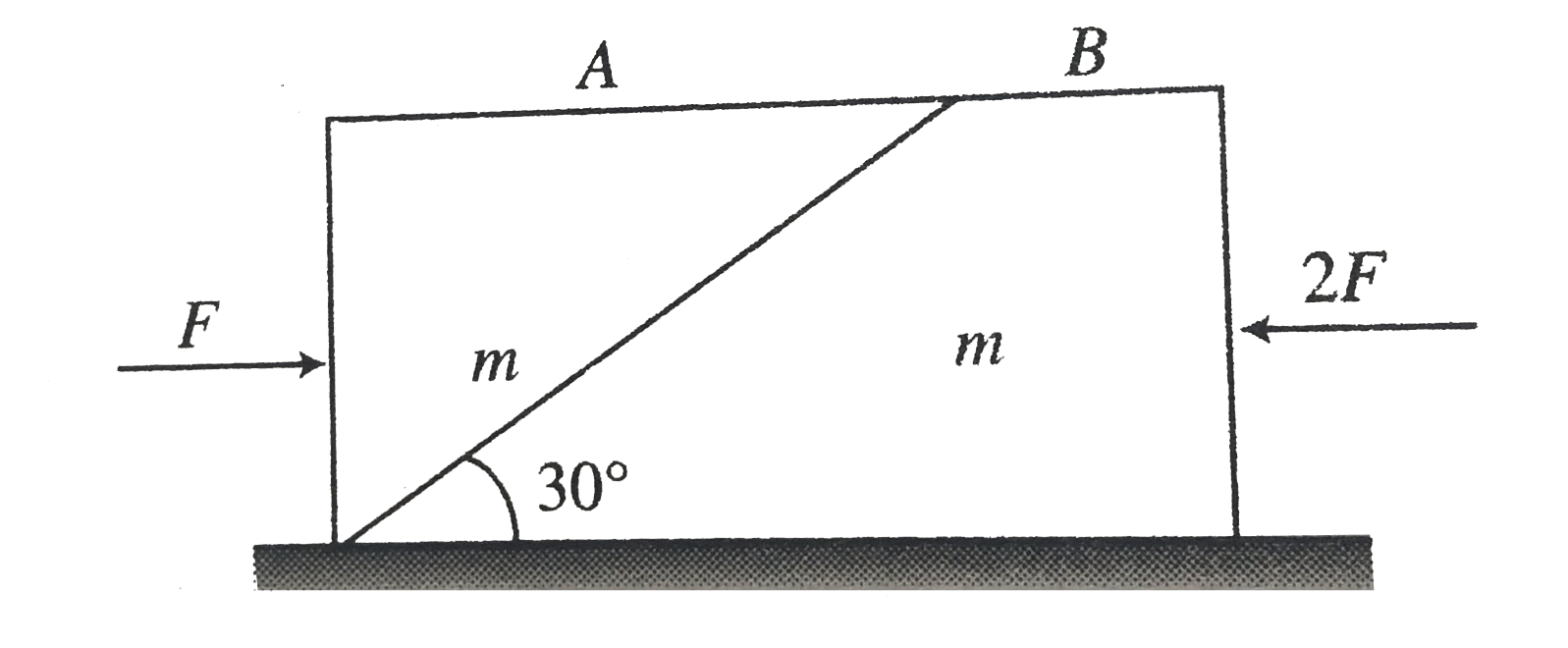
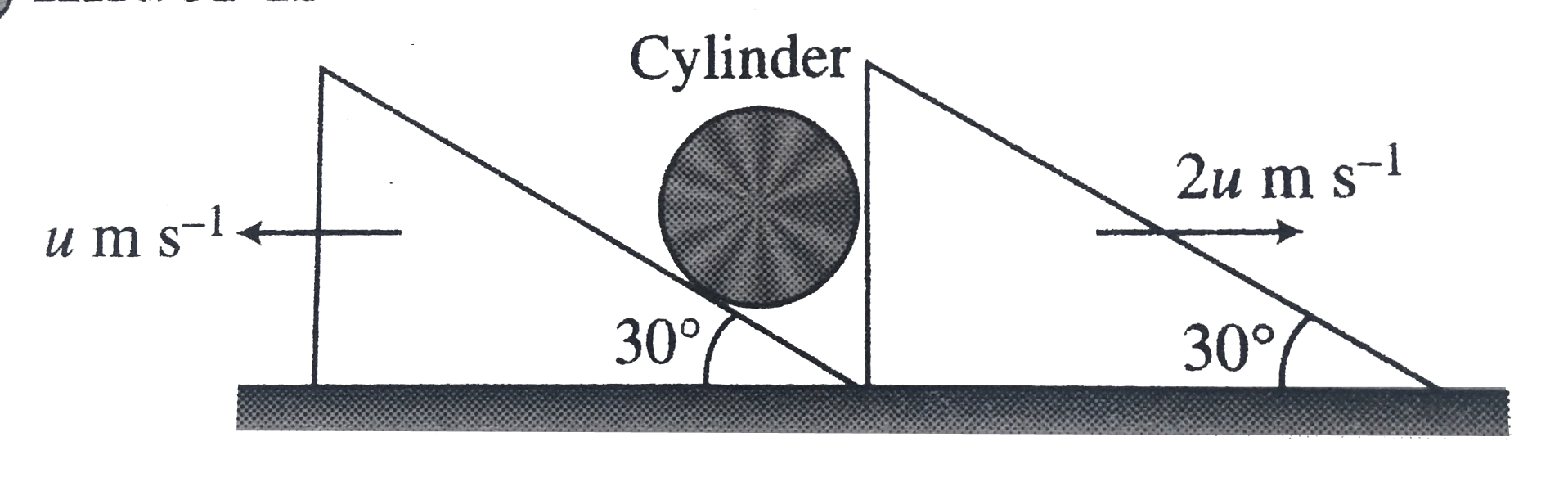
View SolutionA system is shown in fig. Assume that the cylinder remains in contact with the two wedge. Then the velocity of cylinder is
View SolutionA plank is held at an angle `alpha` to the horizontal on two fixed supports A and B. The plank can slide against the supports (without friction) because of the weight Mg `sin alpha`. The acceleration and direction in which a man of mass m should move so that the plank does not move are

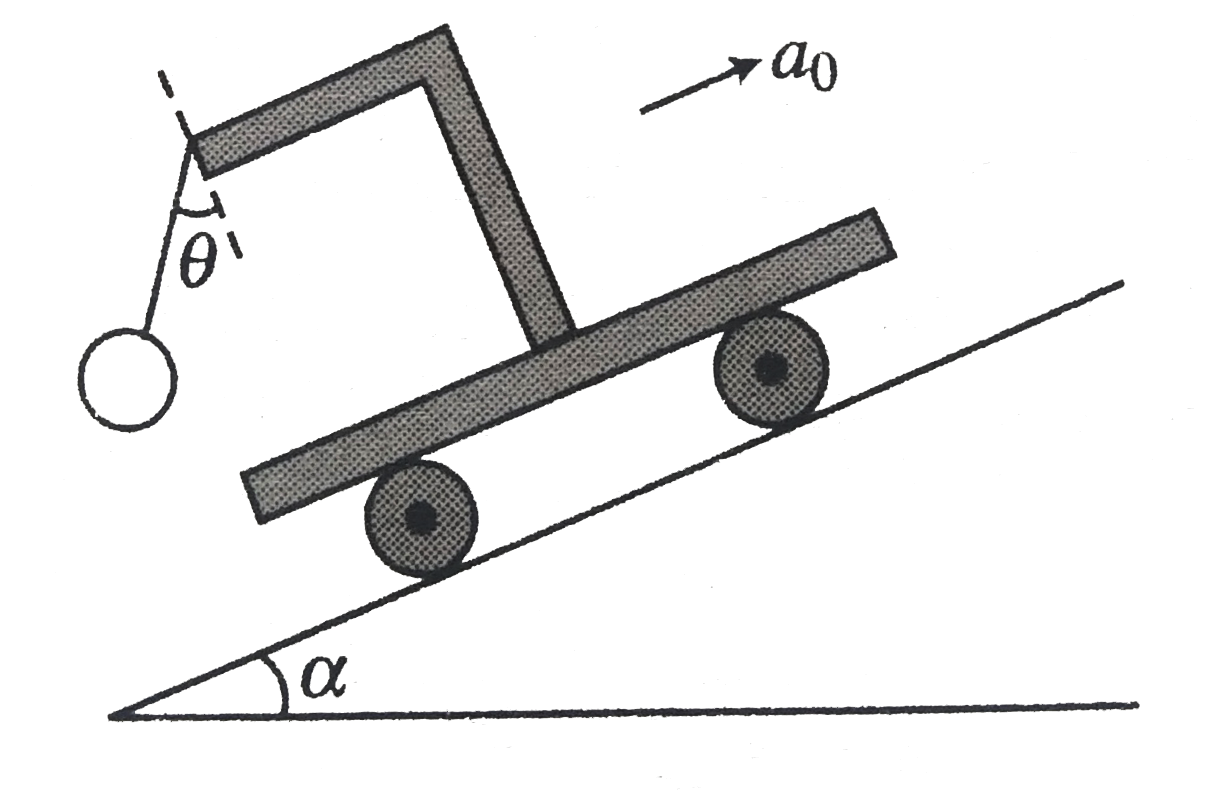
View SolutionA pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination `alpha` with acceleration `a_(0)` is
View SolutionThe acceleration of the block B in fig. Assuming the surfaces and the pulley `P_(1)` and `P_(2)` are all smooth, is

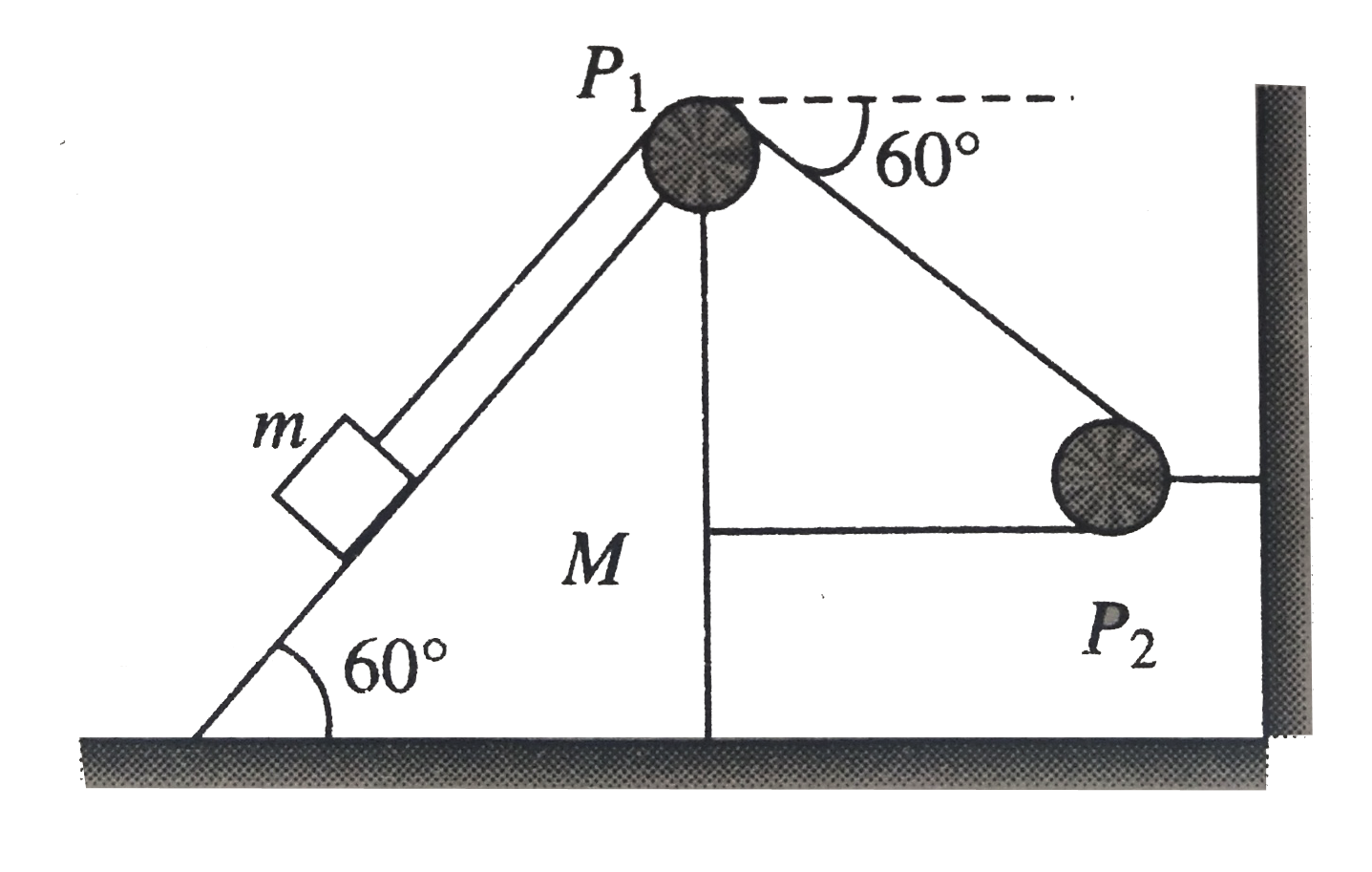
View SolutionIn the arrangement shown in fig. the block of mass `m=2kg` lies on the wedge of mass `M=8kg`. The initial acceleration of the wedge, if the surfaces are smooth, is
View Solution
Single Correct questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 1 of CENGAGE PHYSICS (HINGLISH) of Class 11