Complete Solutions to Exercise 6.3 of chapter NEWTON'S LAWS OF MOTION 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 1 |
| CENGAGE PHYSICS | Exercise 6.3 |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
Block A is given an acceleration `12 ms^(-2)` towards left as shown in fig. Assuming block B always remains horizontal, find the acceleration (in `ms^(-2)`) of B.

View SolutionThe three block shown in fig. move with constant velocities. Find the velocity of blocks A and B. given `V_(P2)=10ms^(-1) darr, V_(C)=2ms^(-1) uarr`.

View SolutionFor the system as shown in fig. find the acceleration of C. the accelerations of A and B with respect to ground are marked.
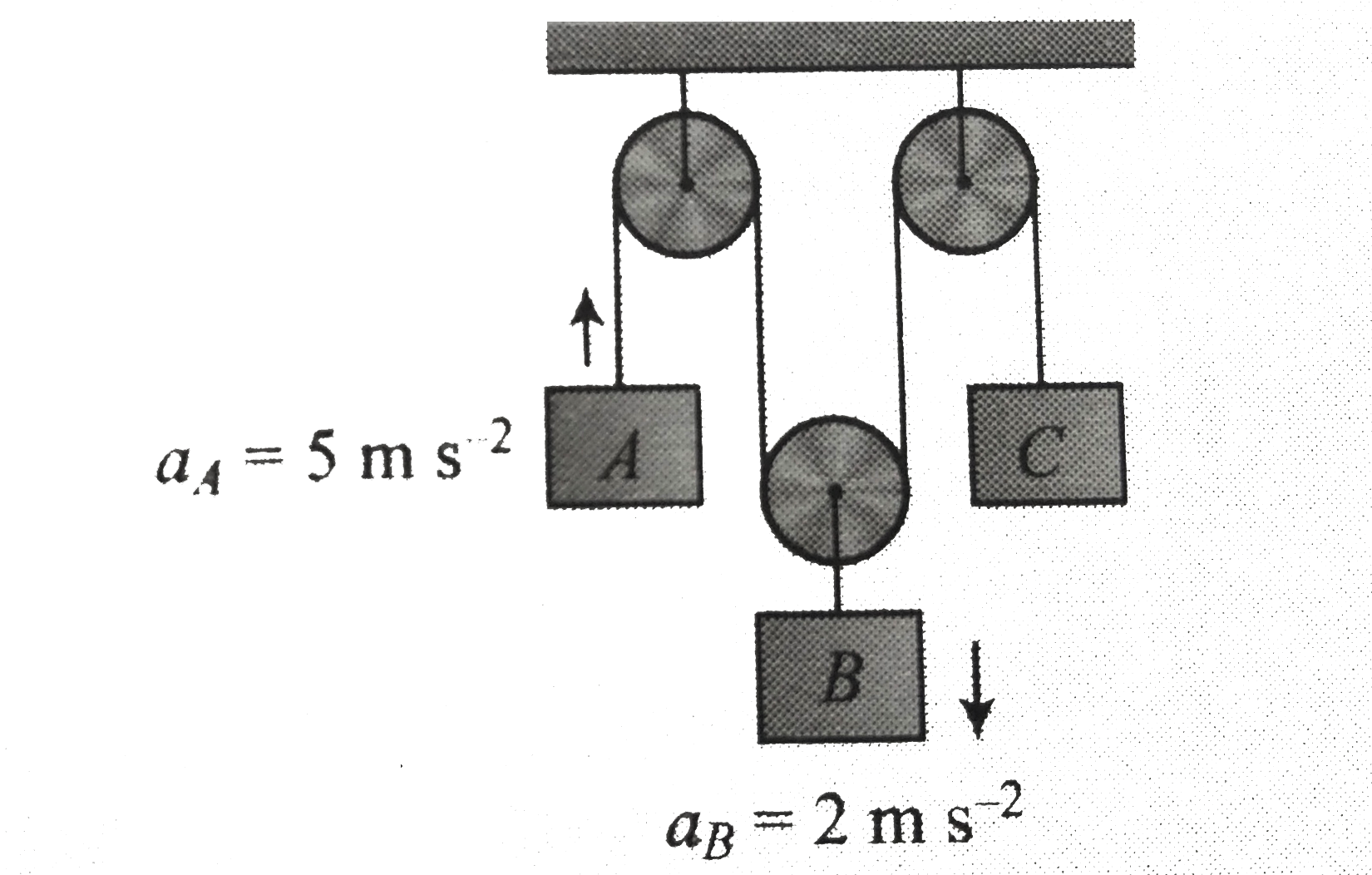
View SolutionSystem is shown in fig. and wedge is moving toward left with speed `2ms^(-1)`. Find the velocity of the block B.

View SolutionIn fig. shown, the speed of the truck is v to the right. Find the speed with which the block is moving up at `theta=60^(@)`.

View SolutionDetermine the speed with which block B rises in fig. if the end of the cord at A is pulled down with a speed of `2ms^(-1)`.

View SolutionAn inextensible string AB is tied to a block B of negligible dimensions and passes over a small pulley C so that free end A hangs h unit above the ground on which the block B rests. In this initial position shown in fig. The free end A is h unit below C. if now end A moves horizontally with a velocity `v_(0)`, obtain an expression for the velocity of the block at any time t.

View SolutionFind the acceleration blocks in fig. The pulley and the string are massless.

View SolutionFigure shows, a system of four pulley with two masses A and B. Find at an instant.

(a) Speed of block A when block B is going up at `1ms^(-1)` and pulley Y is going up at `2 ms^(-1)`.
(b) Acceleration of block A if block B is going up `3 ms^(-2)` and pulley Y is going down at `1 ms^(-2)`.
View SolutionFigure shows a pulley over which is string passes and connected to two masses A and B. Pulley moves up with a velocity `V_(P)` and mass B is also going up at a velocity `V_(B)`.

Find the velocity of mass A if
(a) `V_(P)=5ms^(-1)` and `V_(B)=10ms^(-1)`
(b) `V_(P)=5ms^(-1)` and `V_(B)=-20 ms_(-1)`.
View SolutionFind the relation in the accelerations of the three masses shown in fig.
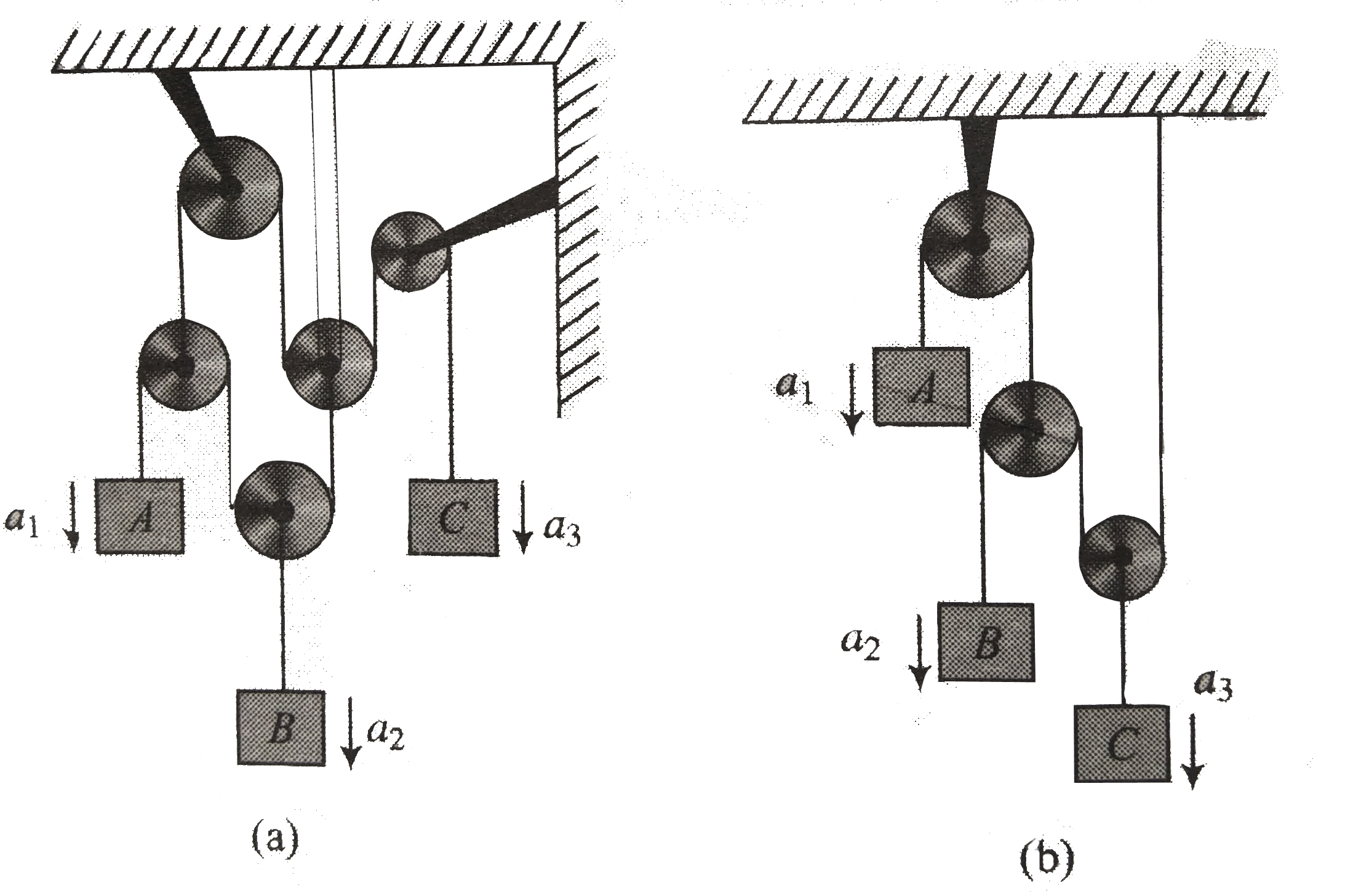
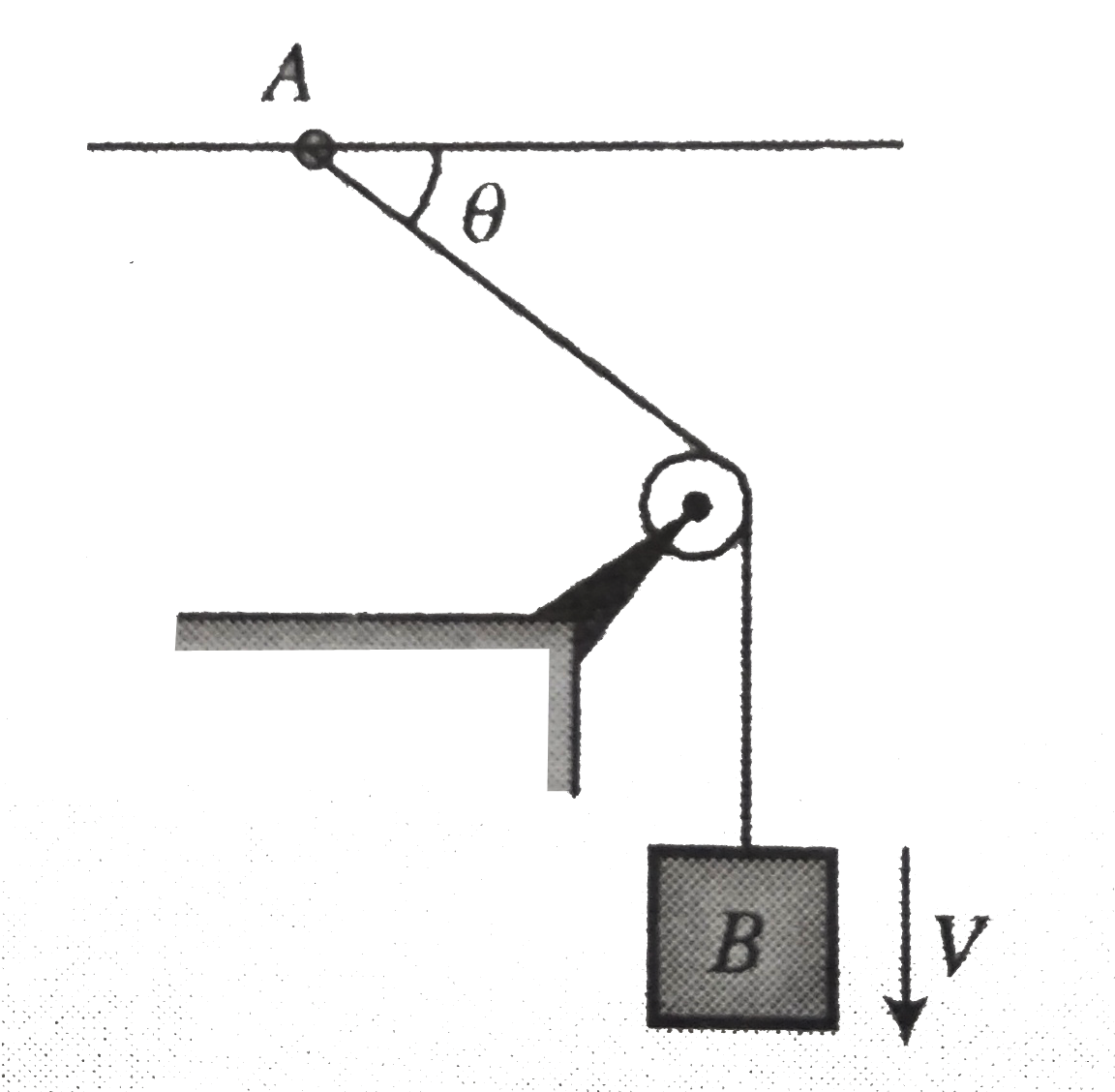
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle `theta` with the wire and mass B is going down with a velocity v.
View SolutionFigure shows a block A constrained to slide along the inclined plane of the wedge B shown. Block A is attached with a string which passes through three ideal pulleys and connected to the wedge B. If wedge is pulled toward right with an acceleration a, find
(a) the acceleration of the block with respect to wedge
(b) the acceleration of the block with respect to ground.

View SolutionFind the acceleration of block B as shown in fig. (a) and (b) relative to block A and relative to ground if block A is moving toward right with acceleration a.

View SolutionIf the string is inextensible, determine the velocity u of each block in terms of v and `theta`.

(a) fig a: u=…
(b) fig.(b): u=….
View SolutionCalculate the acceleration of block A and B in cases (a),(b), and (c ).



View SolutionA rod of mass m is supported on a wedge of mass M shown in fig. Find the accelerations of rod a and wedge A in the arrangment. The friction between all contact surfaces in negligible.

View SolutionIn fig, no relative motion takes place between the wedge and the block placed on it. The rod slides down wards over the wedge and pushes the wedge to move in horizontal direction, The mass of wedge is same as that of the block and is equal to M. If `tan theta=(1//sqrt(3))`, find the mass of rod. (Neglect rotation of the rod).
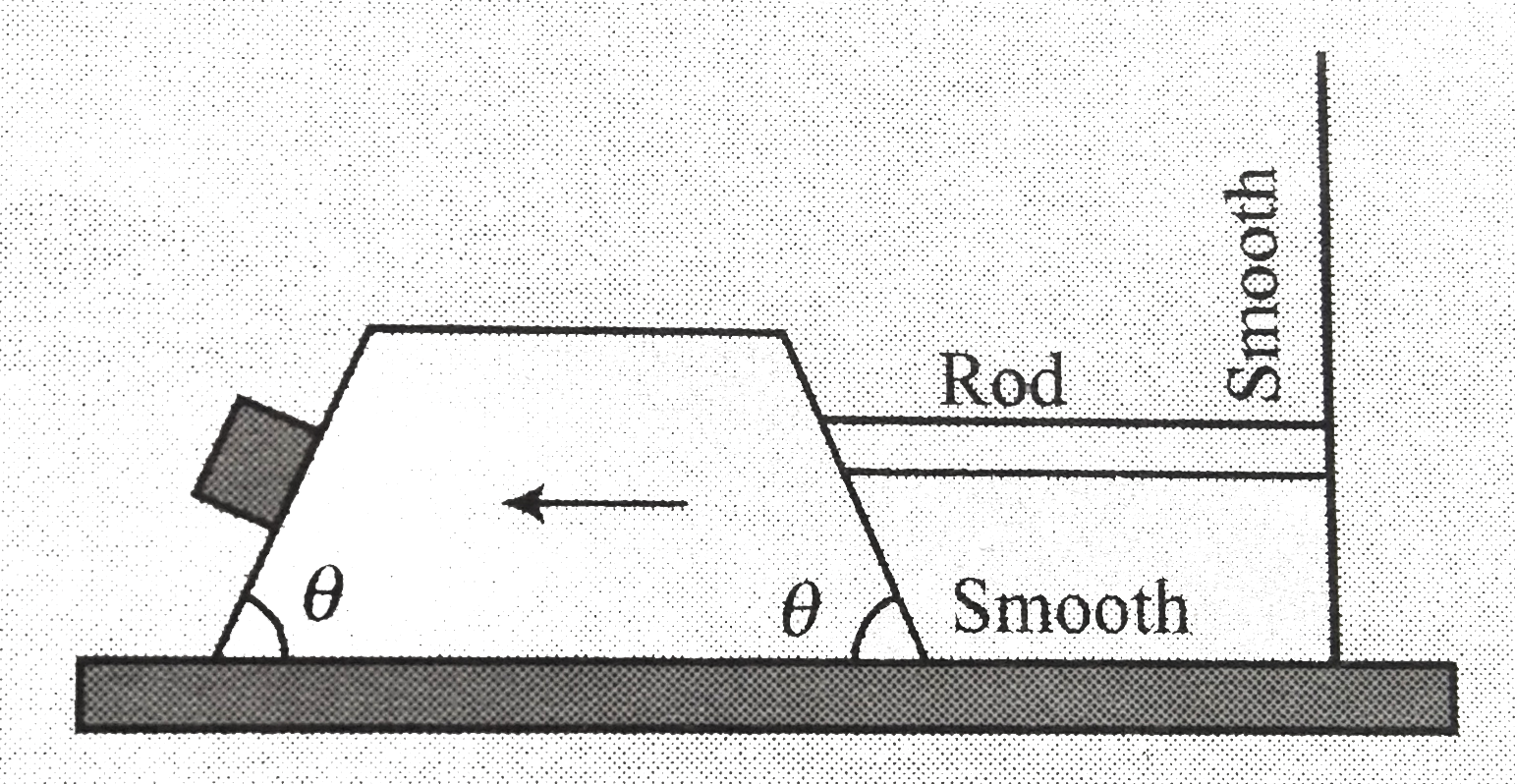
View SolutionThe velocities of A and B shown in fig. Find the speed (in `ms^(-1)`) of block C. (Assume that the pulleys and string are ideal).

View Solution
Exercise 6.3 questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 1 of CENGAGE PHYSICS (HINGLISH) of Class 11