Complete Solutions to Linked Comprehension of chapter WORK, POWER & ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, POWER & ENERGY |
| CENGAGE PHYSICS | Linked Comprehension |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
Two unequal masses are ties together with a cord with a compressed spring in between.
When the cord is burnt with a match releasing the spring, the two masses fly apart with equal
View SolutionTwo unequal masses are ties together with a cord with a compressed spring in between.
Which one is correct?
View SolutionTwo unequal masses are ties together with a cord with a compressed spring in between.
Which of the following energies is conserved for the system?
View SolutionA body of mass
The power exerted on the body at
View SolutionA body of mass
Find average power transferred to the body in first
View SolutionSand particles drop vertically at the rate of
The extra force required to keep the belt moving is
View SolutionSand particles drop vertically at the rate of
The extra force required is
View SolutionSand particles drop vertically at the rate of
The time rate of change of kinetic energy of sand particles is
View SolutionA ladder of length
The potential energy of the man
View SolutionA ladder of length
The potential energy of the balloon
View SolutionA ladder of length
The work done by the man is
View SolutionA single conservative force
What is the mechanical energy of a system?
View SolutionA single conservative force
The maximum and minimum values of x, respectively, are
View SolutionA single conservative force
The maximum kinetic energy of the particle and the value of x at which maximum kinetic energy occurs are
View SolutionA single conservative force
Determine the equation of
View SolutionA
The maximum kinetic energy of the block between
View SolutionA
The maximum positive displacement x is
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where
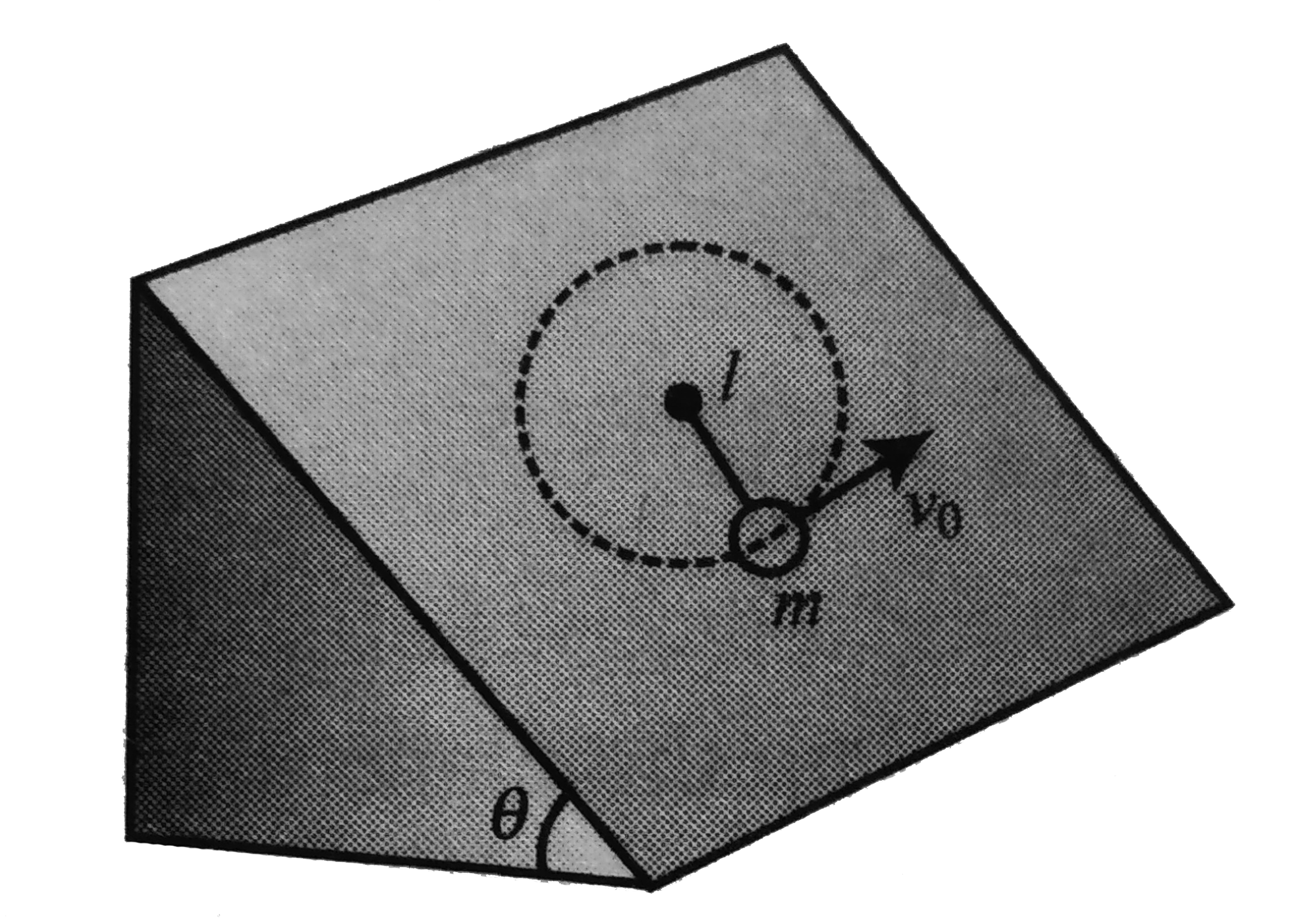
The speed of the bob at the lowest point is
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where
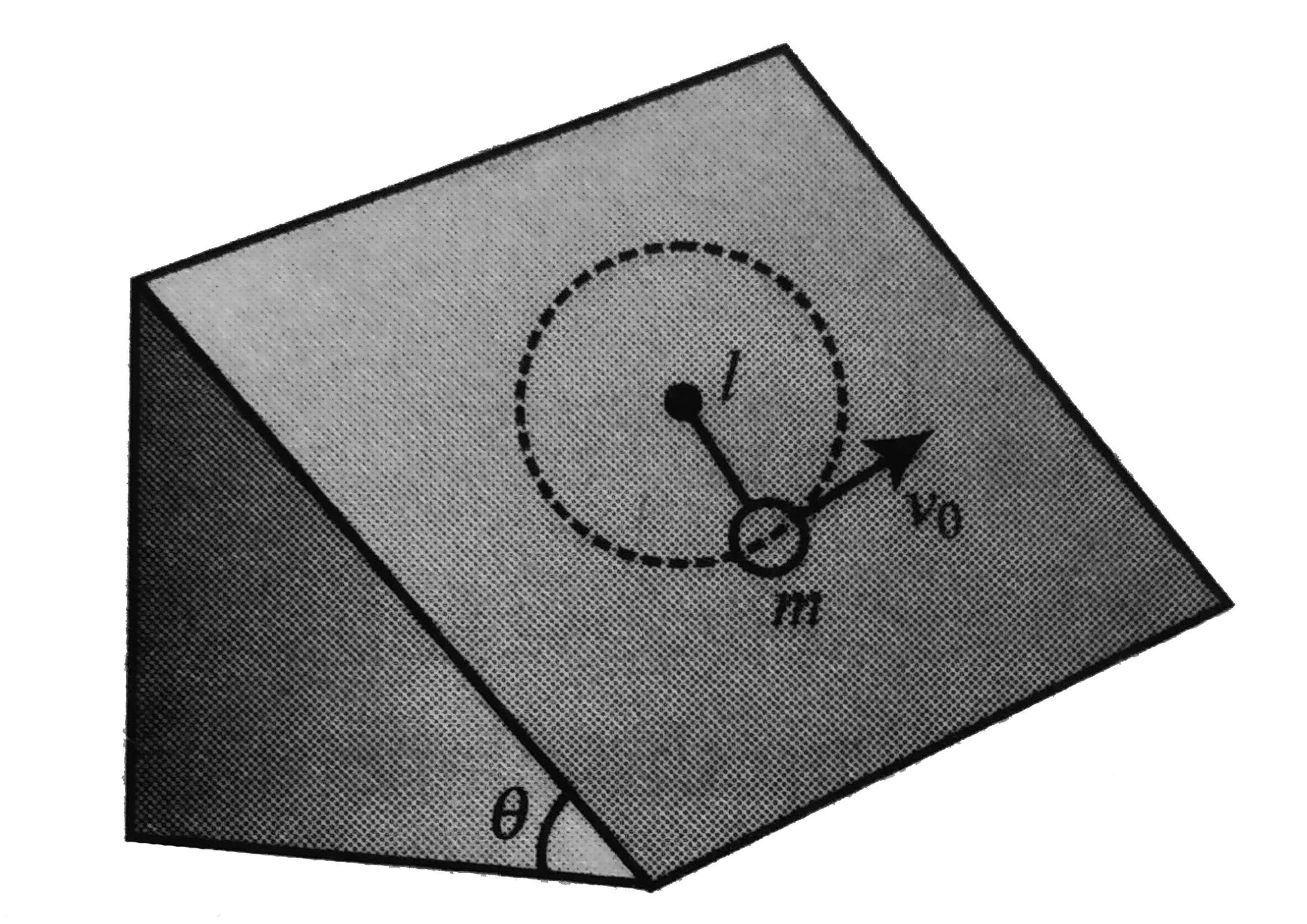
The speed of the bob at the highest point on the circle is
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where
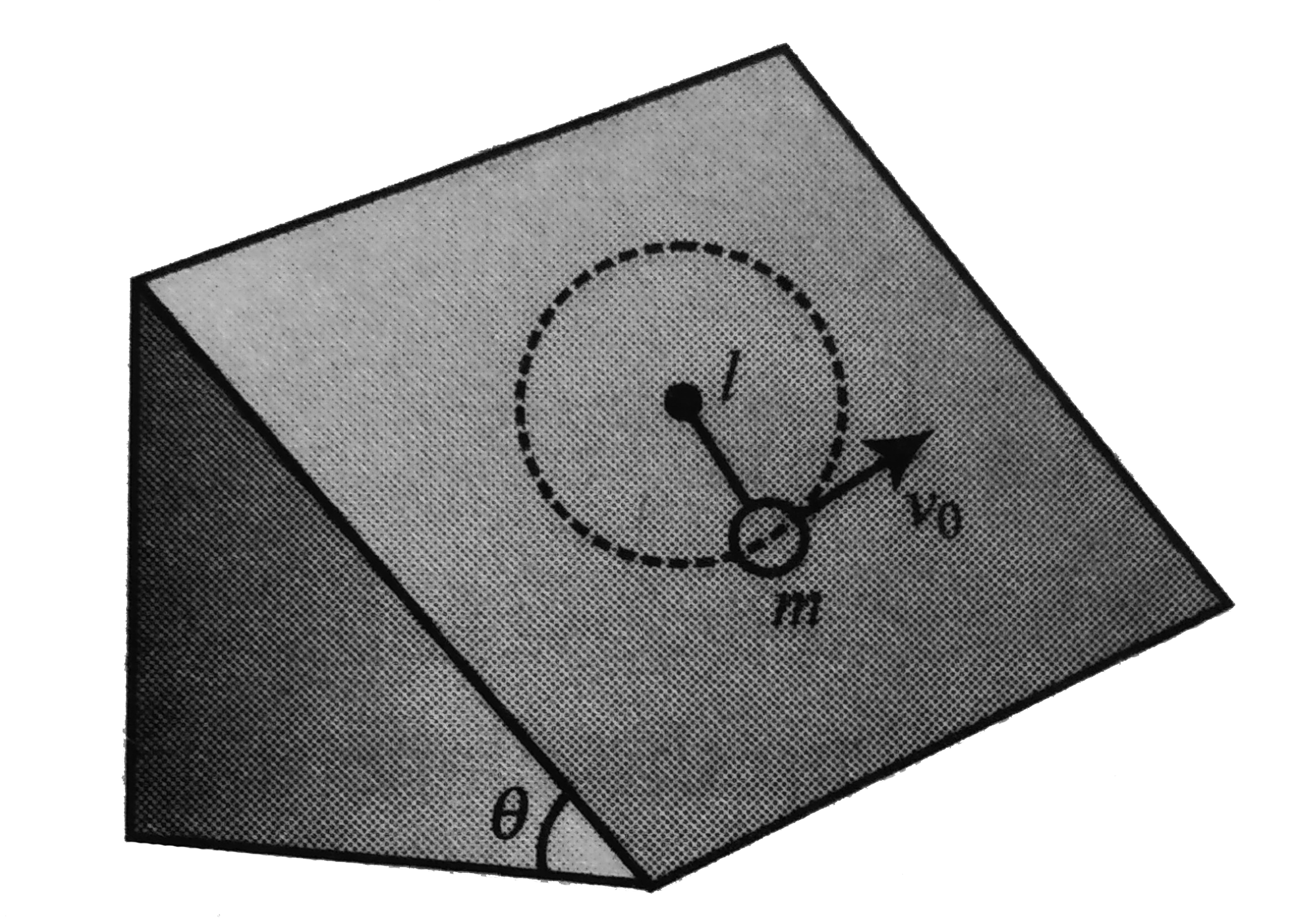
The tension in the string at the highest position is
View SolutionA small ball is rolled with speed

Determine the required speed u so that the ball returns to A, the point of projection after passing through C, the highest point.
View SolutionA small ball is rolled with speed

`What is the minimum value of x for which the ball can reach the point of projection after reaching C?
View SolutionA man of mass
Which of the following options is correct regarding the various work done?
View SolutionA man of mass
If instead of moving up the plane, the man increases his speed to the value v while moving down the inclined plane through the same vertical distance h, then
View SolutionA man of mass
If in the previous problem, we replace the man by a block of mass m and release it from top of the inclined plane, and let it gain a speed v, then
View SolutionA boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is
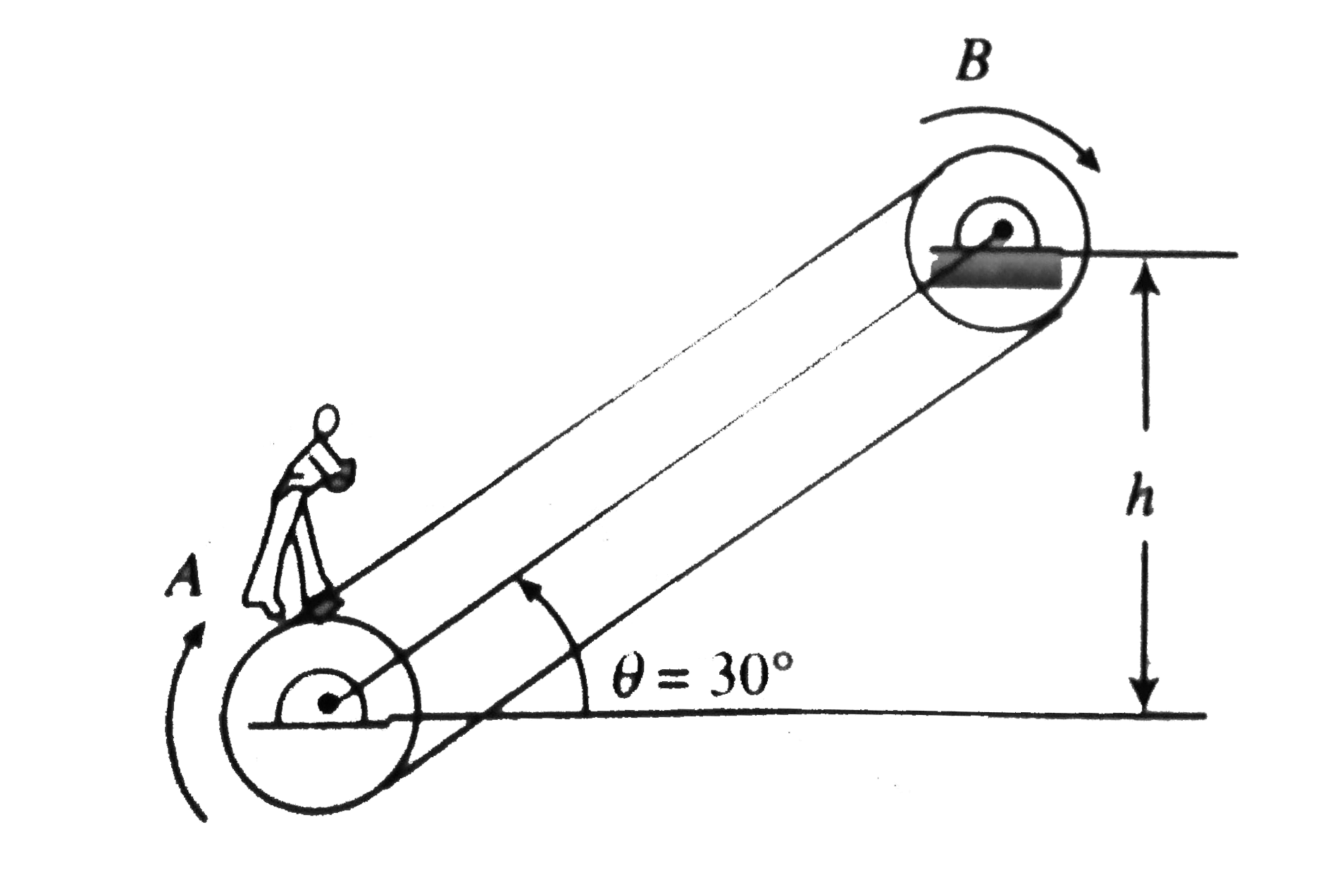
The time taken by the boy to reach the height h is
View SolutionA boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is
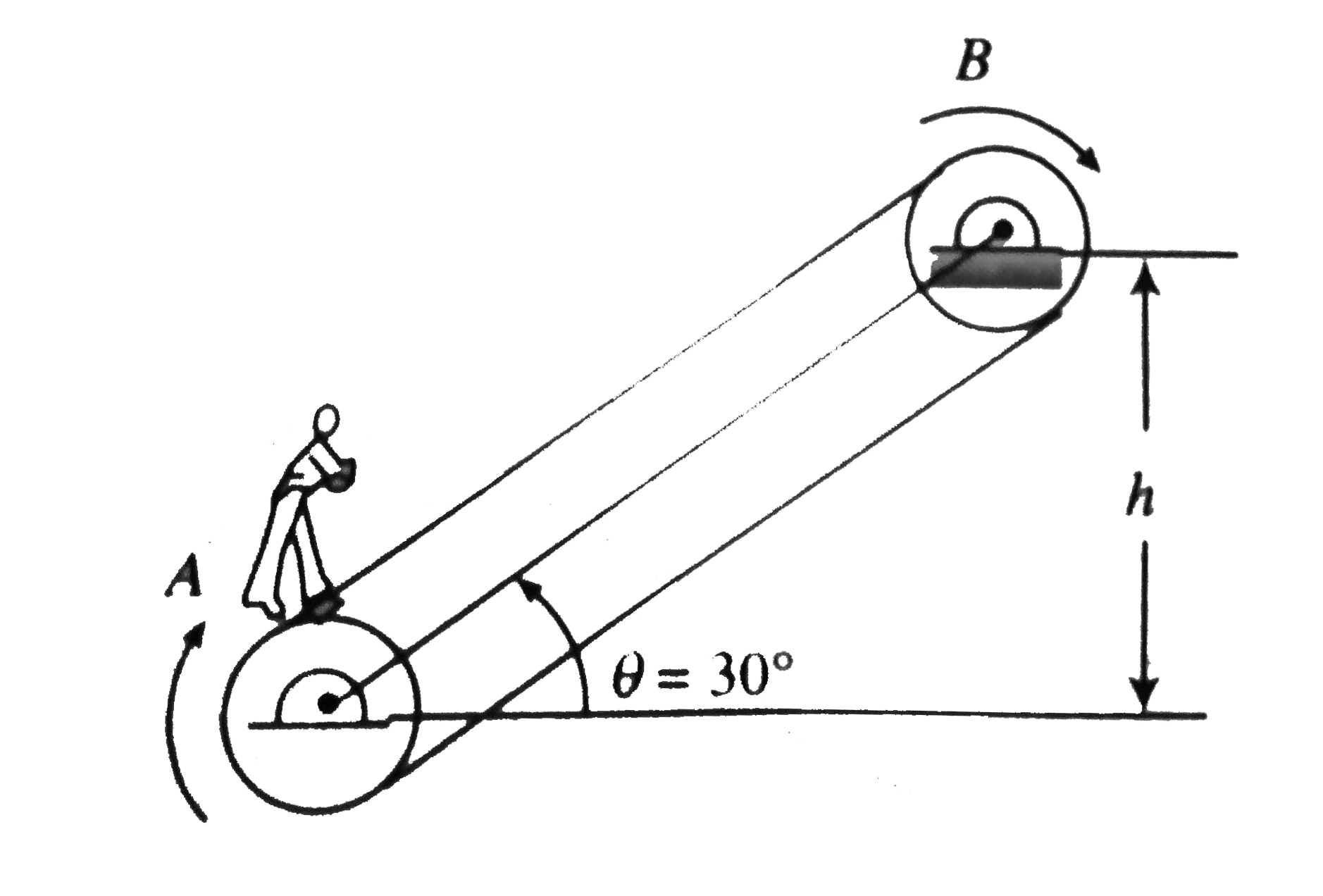
Work done by gravity to w.r.t. the conveyor belt is
View SolutionA boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is

Work done by friction on the boy is
View SolutionA boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is
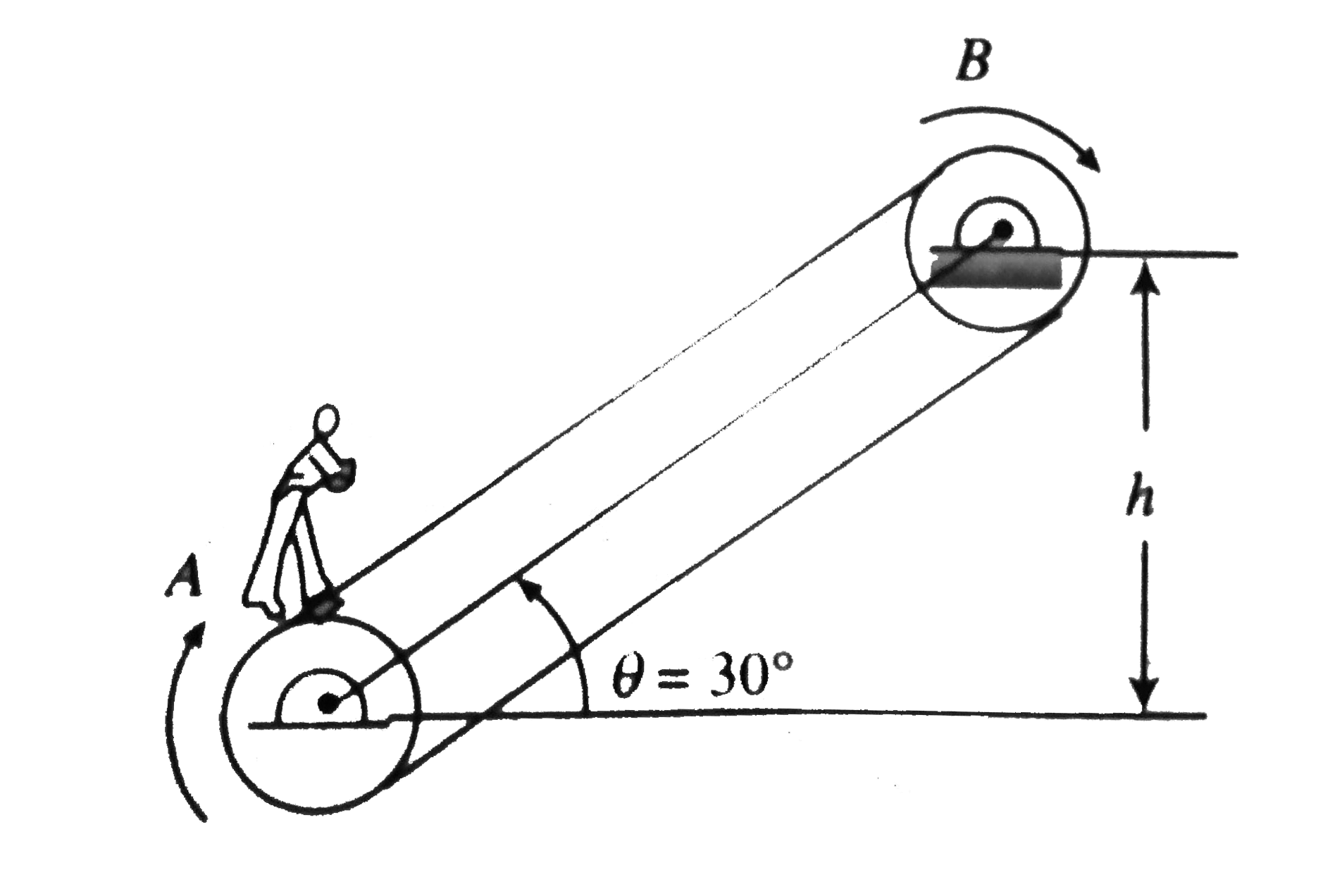
Work done by the boy is
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is
ii. Mass of camel is
iii. Load is accelerated for first
iv. From biological data, the rate of consumption of energy of camel can be expressed as
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively are
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is
ii. Mass of camel is
iii. Load is accelerated for first
iv. From biological data, the rate of consumption of energy of camel can be expressed as
(Assuming that the camel exerts a horizontal force on the load):
The ratio of magnitude of work done by camel on the load during accelerated motion to retarded motion is
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is
ii. Mass of camel is
iii. Load is accelerated for first
iv. From biological data, the rate of consumption of energy of camel can be expressed as
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load is
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is
ii. Mass of camel is
iii. Load is accelerated for first
iv. From biological data, the rate of consumption of energy of camel can be expressed as
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is
ii. Mass of camel is
iii. Load is accelerated for first
iv. From biological data, the rate of consumption of energy of camel can be expressed as
(Assuming that the camel exerts a horizontal force on the load):
The total energy consumed by the camel during the trip of
View SolutionA srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at
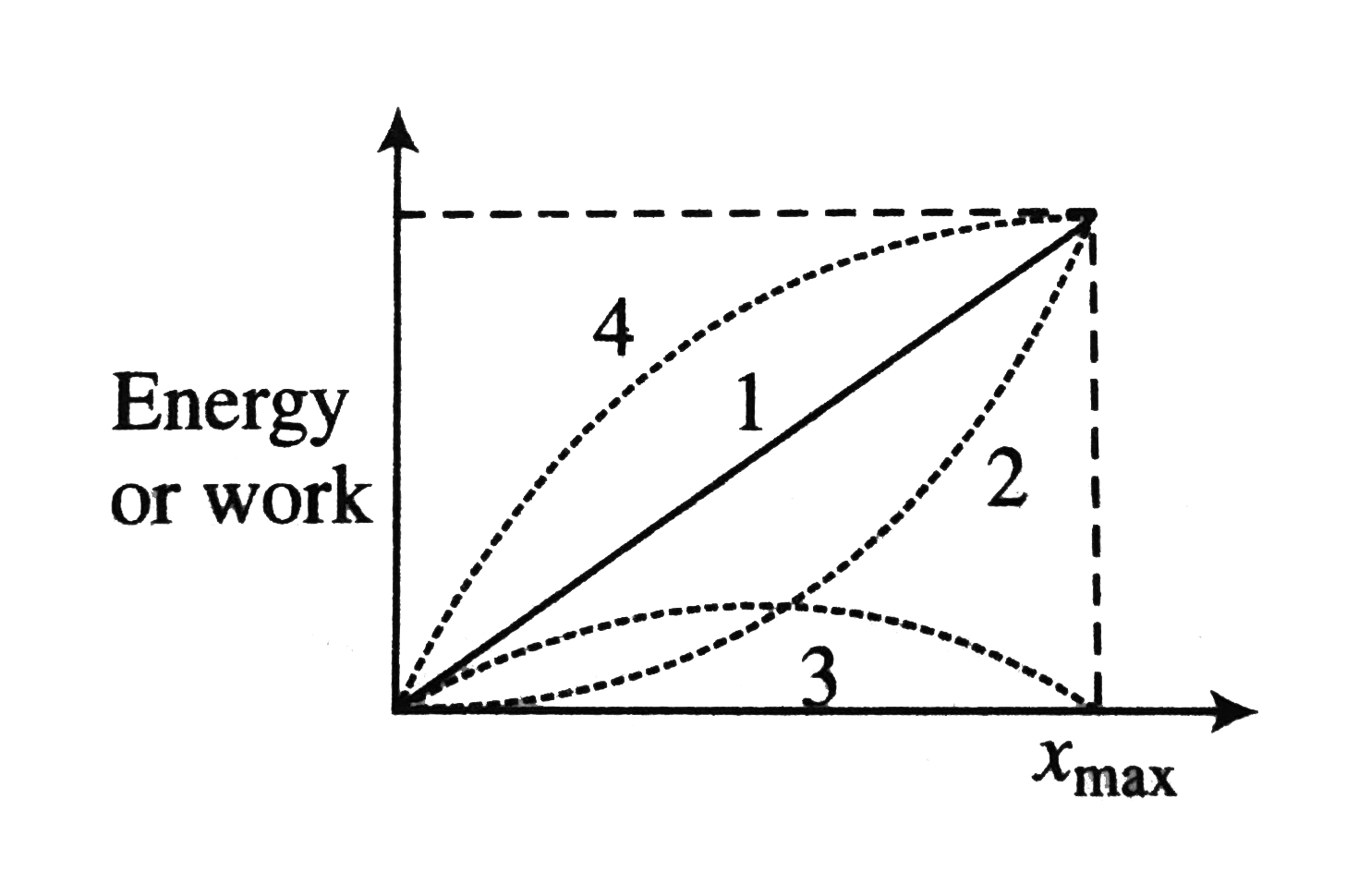
During the displacement, which of the curves shown in the graph best represents the kinetic energy of the block?
View SolutionA srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at
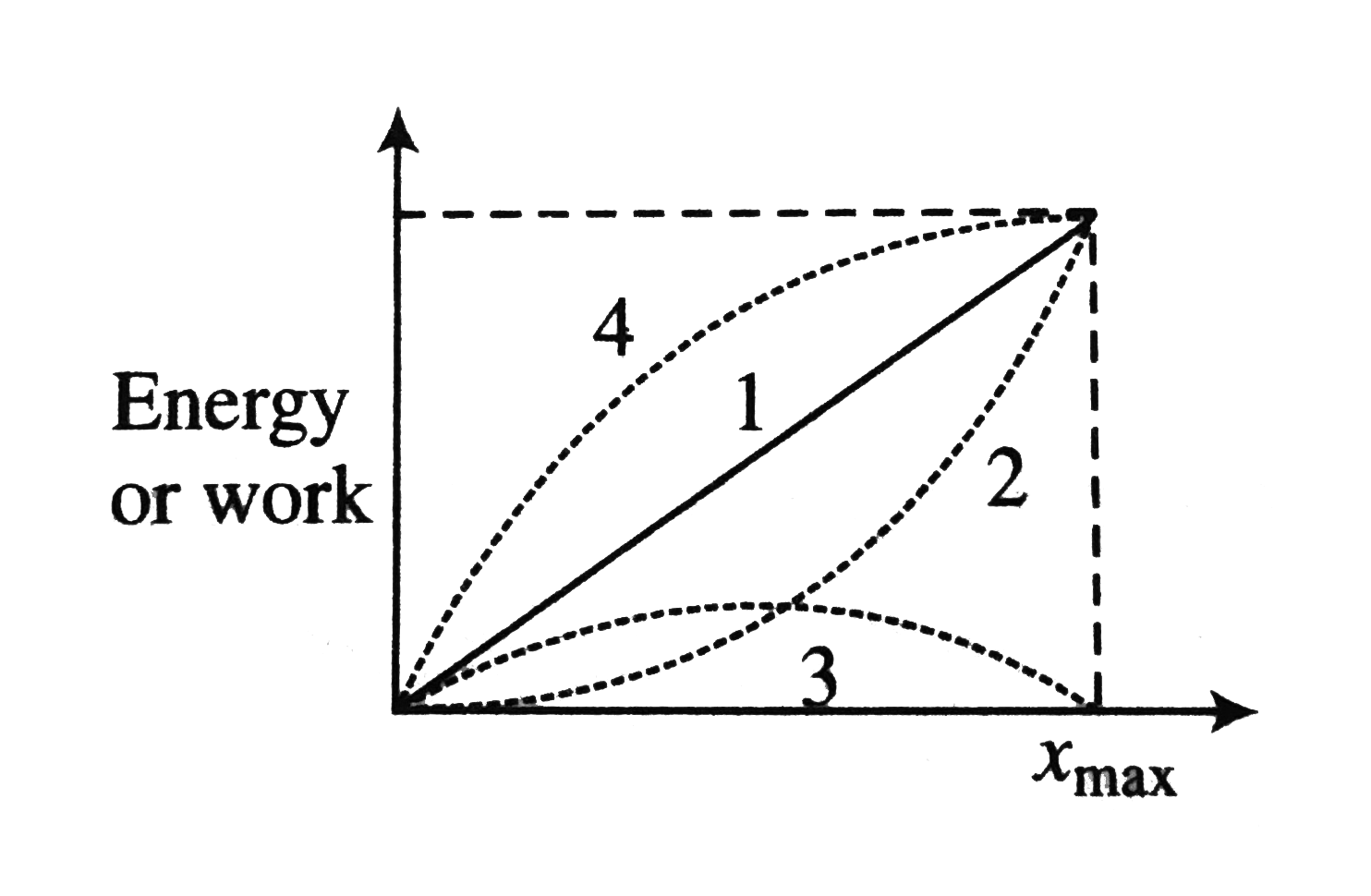
During the displacement, which of the curves shown in the graph best represents the work done on the spring block system by the applied force?
View SolutionA srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at
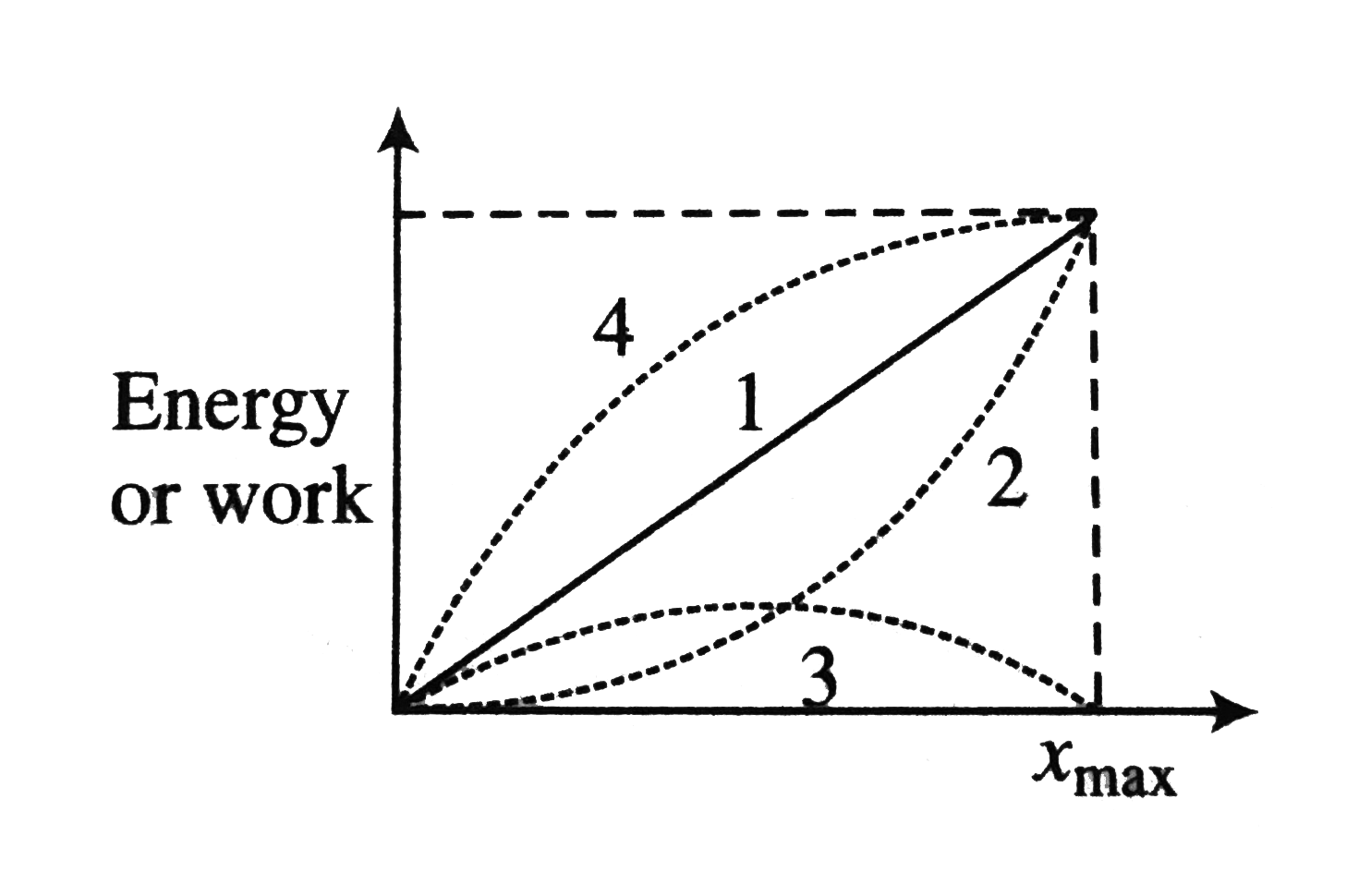
During the first half of the motion, applied force transfers more energy to the
View SolutionA small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width
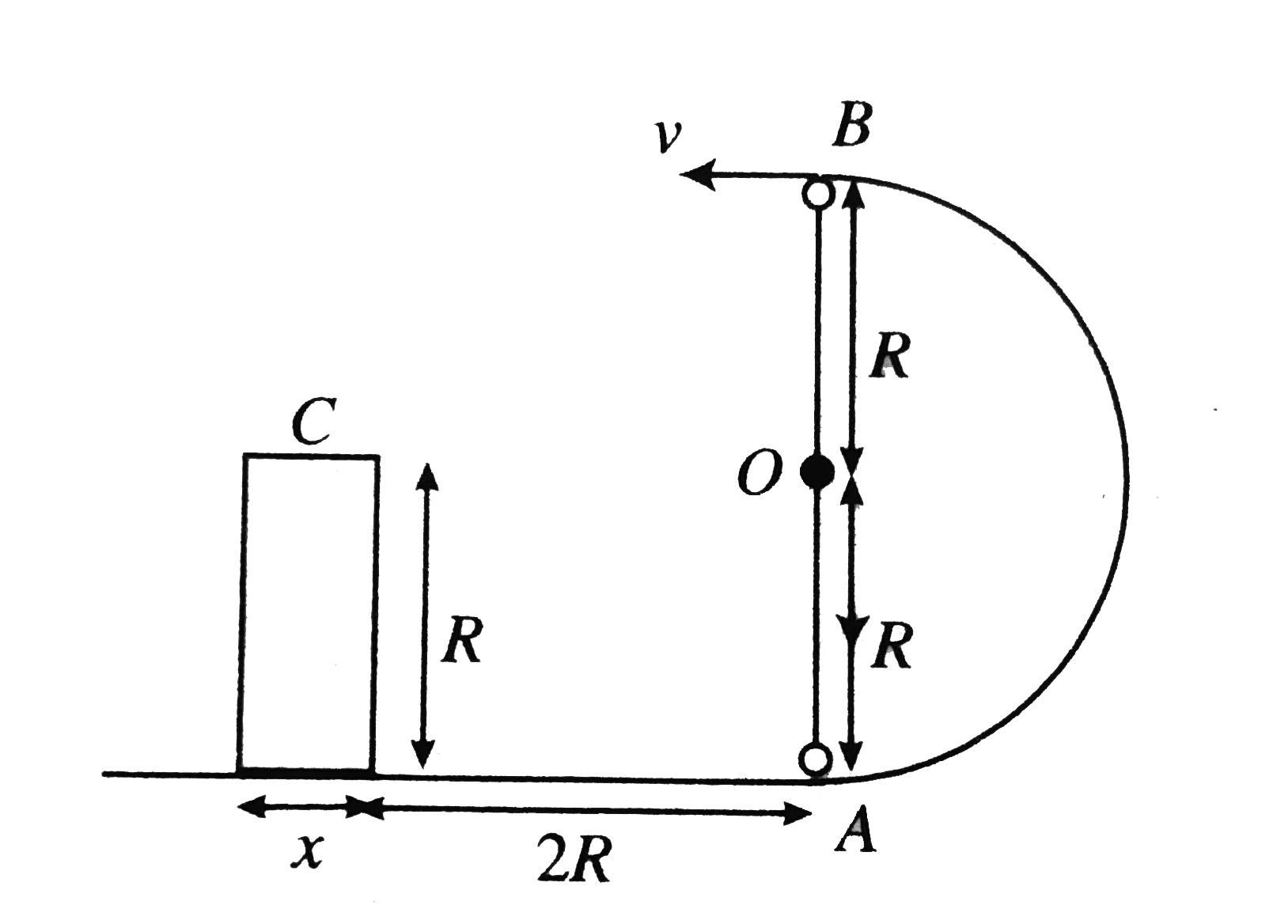
The velocity given to the ball at point A so that it may hit the top of the building is
View SolutionA small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width
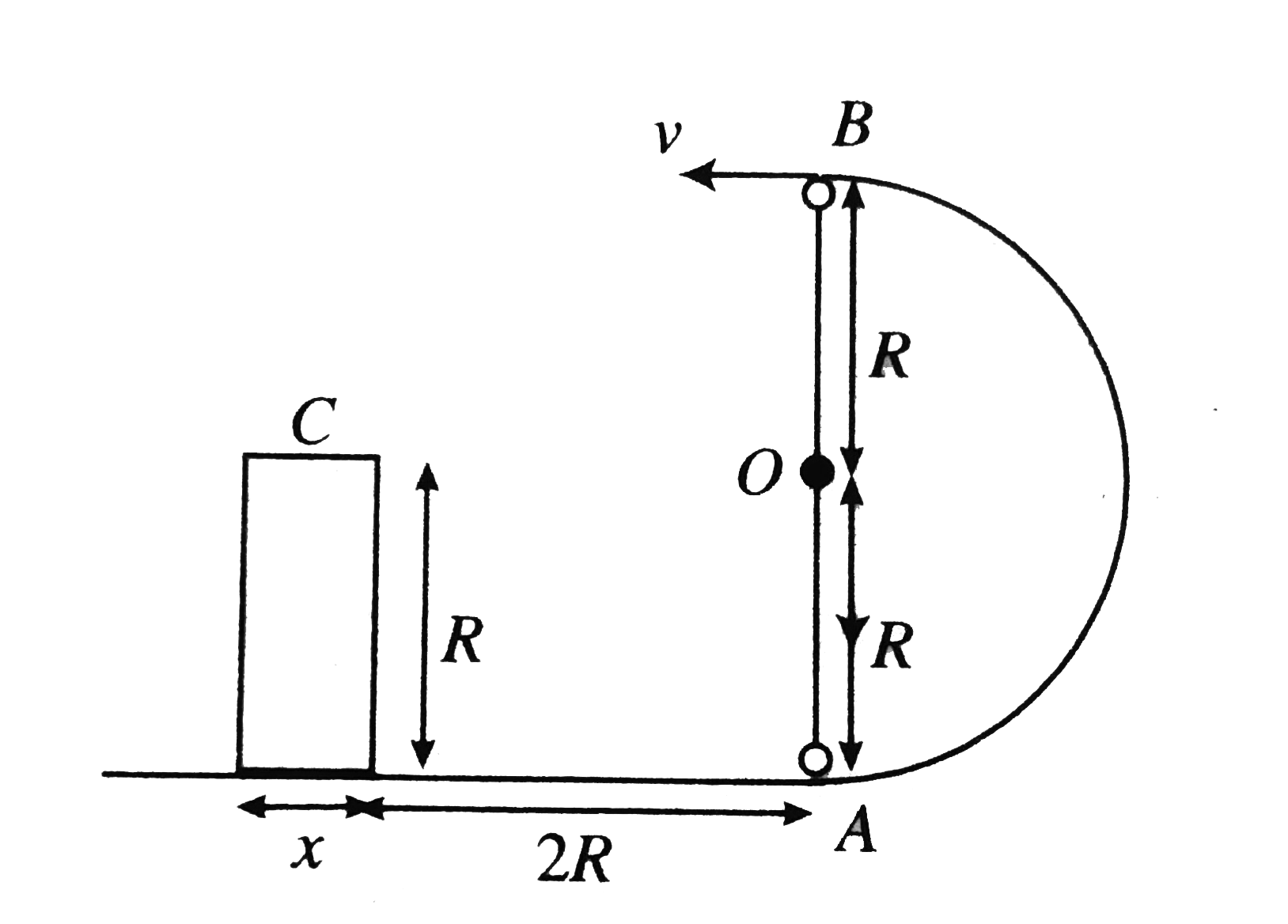
If the collision of ball with the building is elastic, then the angle with the horizontal at which the ball will rebound from the top of the building is
View SolutionA small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width
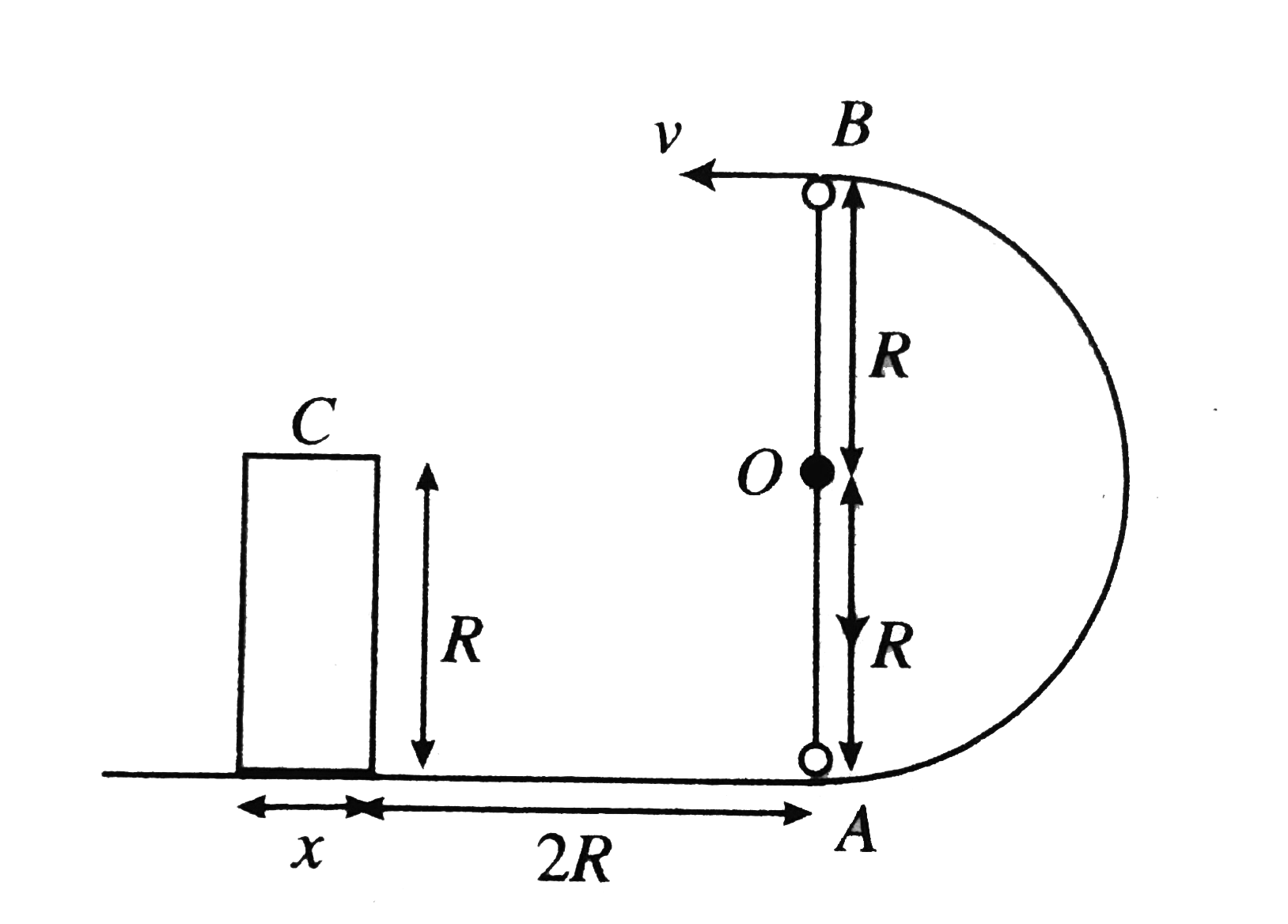
The horizontal distance of the ball from the foot of the builing where the ball strikes the horizontal ground will
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on
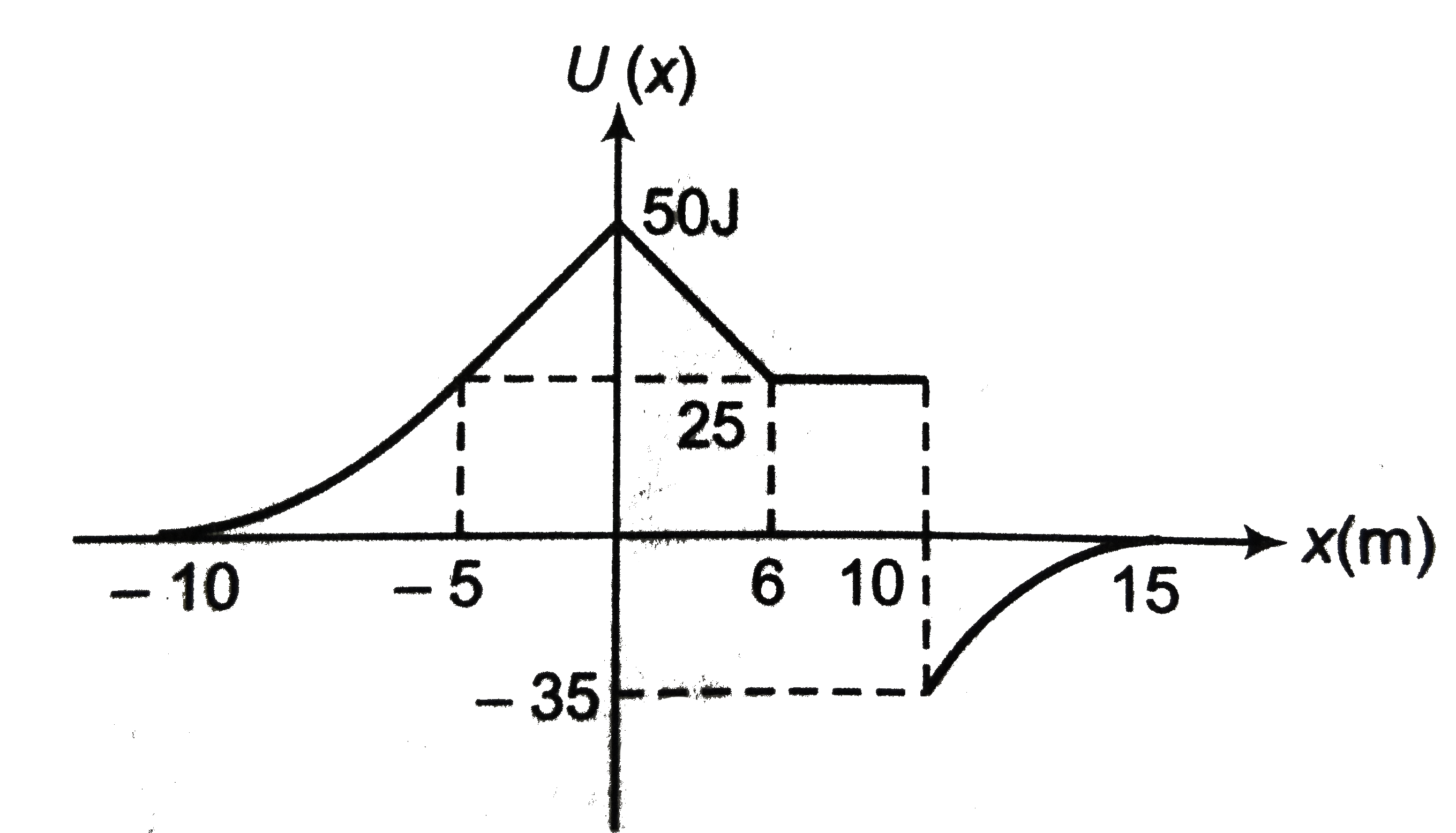
If total mechanical energy of the particle is
View SolutionFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e.,
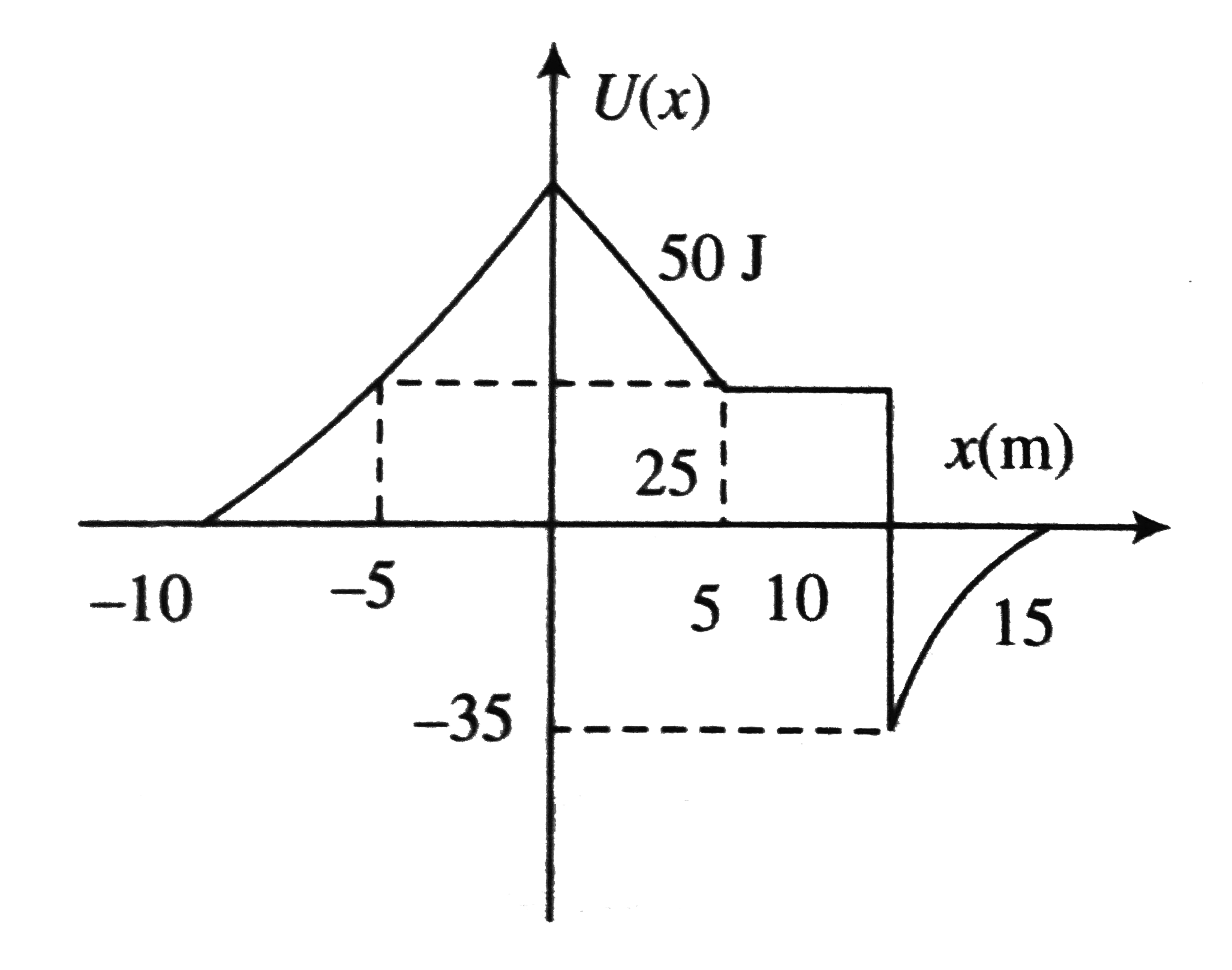
If the total mechanical energy of the particle is
View SolutionFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e.,

If the particle is isolated and its total mechanical energy is
View SolutionForce acting on a particle moving in the x-y plane is
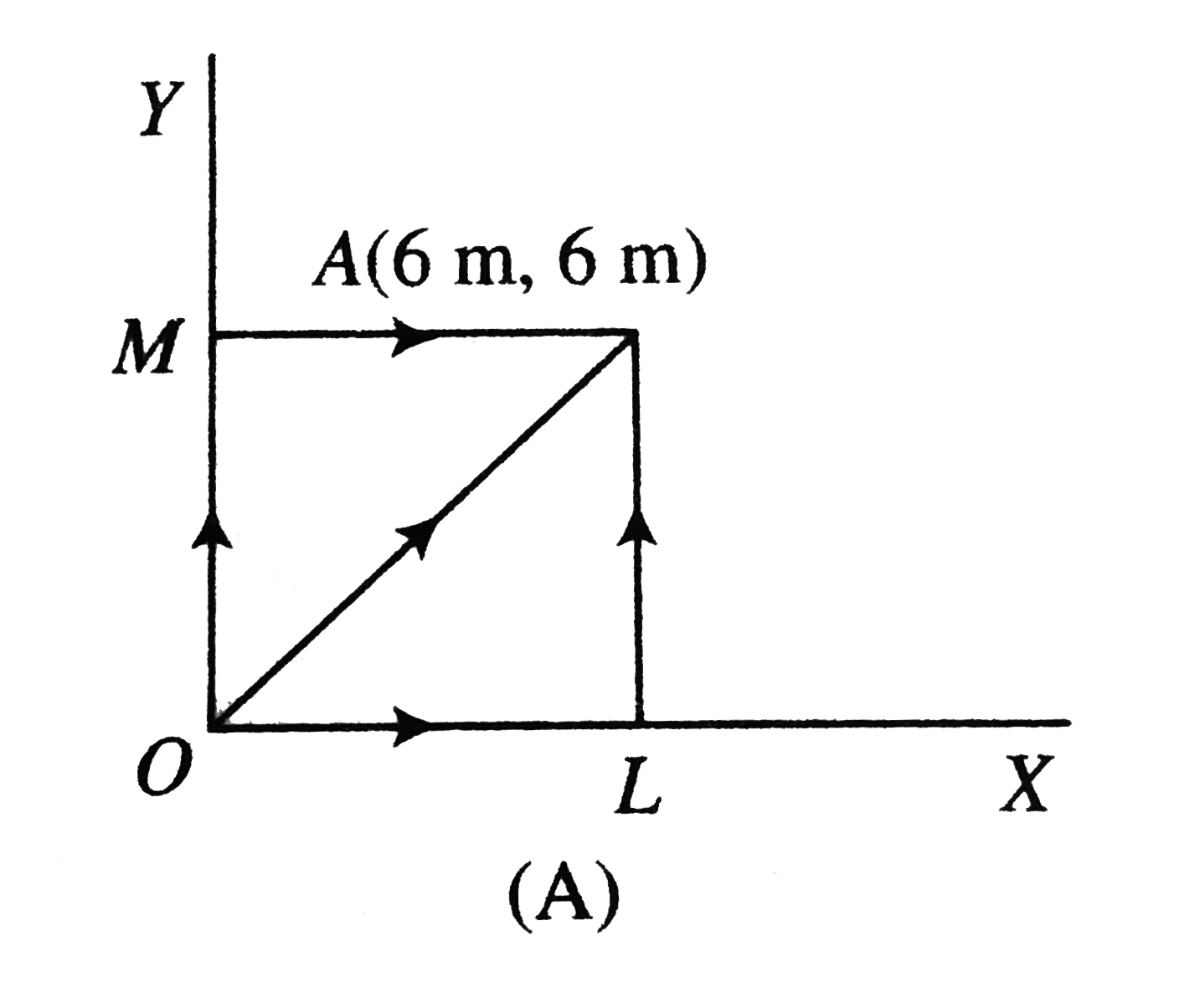
Which of the following is correct?
View SolutionForce acting on a particle moving in the x-y plane is

Which of the following is correct?
View SolutionForce acting on a particle moving in the x-y plane is
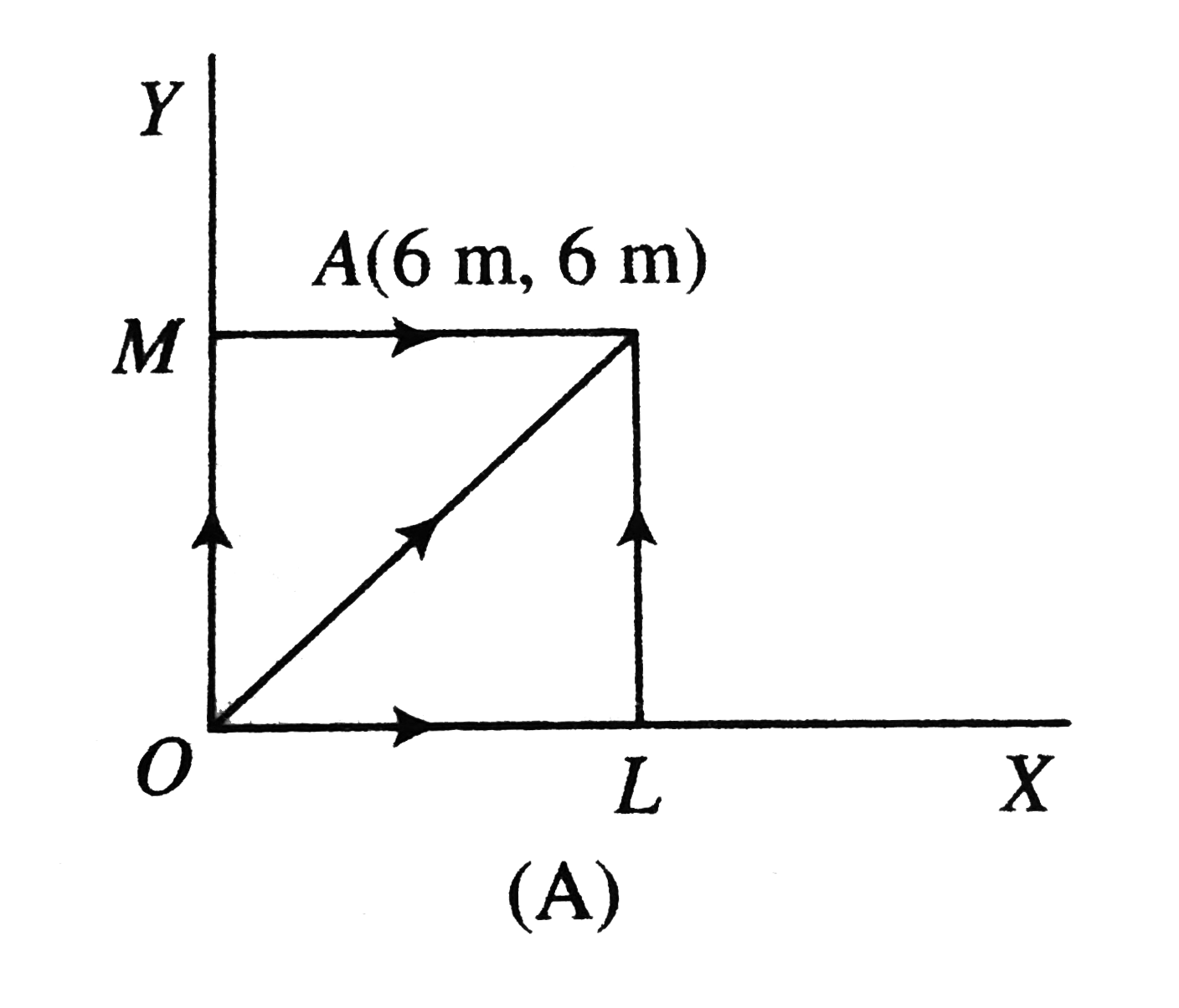
Work done for motion along path OA is nearly
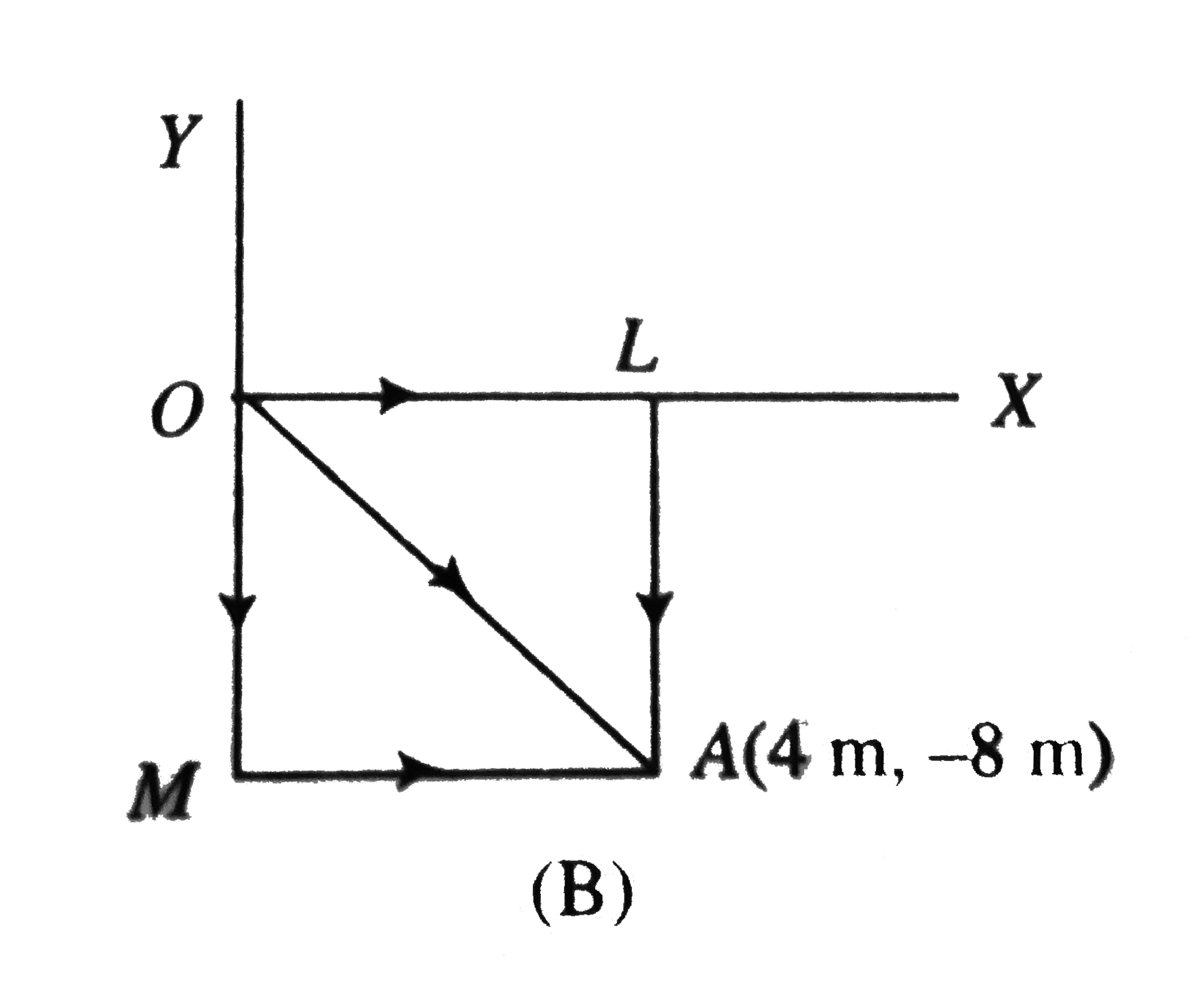
View SolutionForce acting on a particle moving in the x-y plane is

Which of the following is correct?
View SolutionForce acting on a particle moving in the x-y plane is
Now consider another situation. A force

Speed of the particle at A will be nearly
View SolutionForce acting on a particle moving in the x-y plane is
Now consider another situation. A force
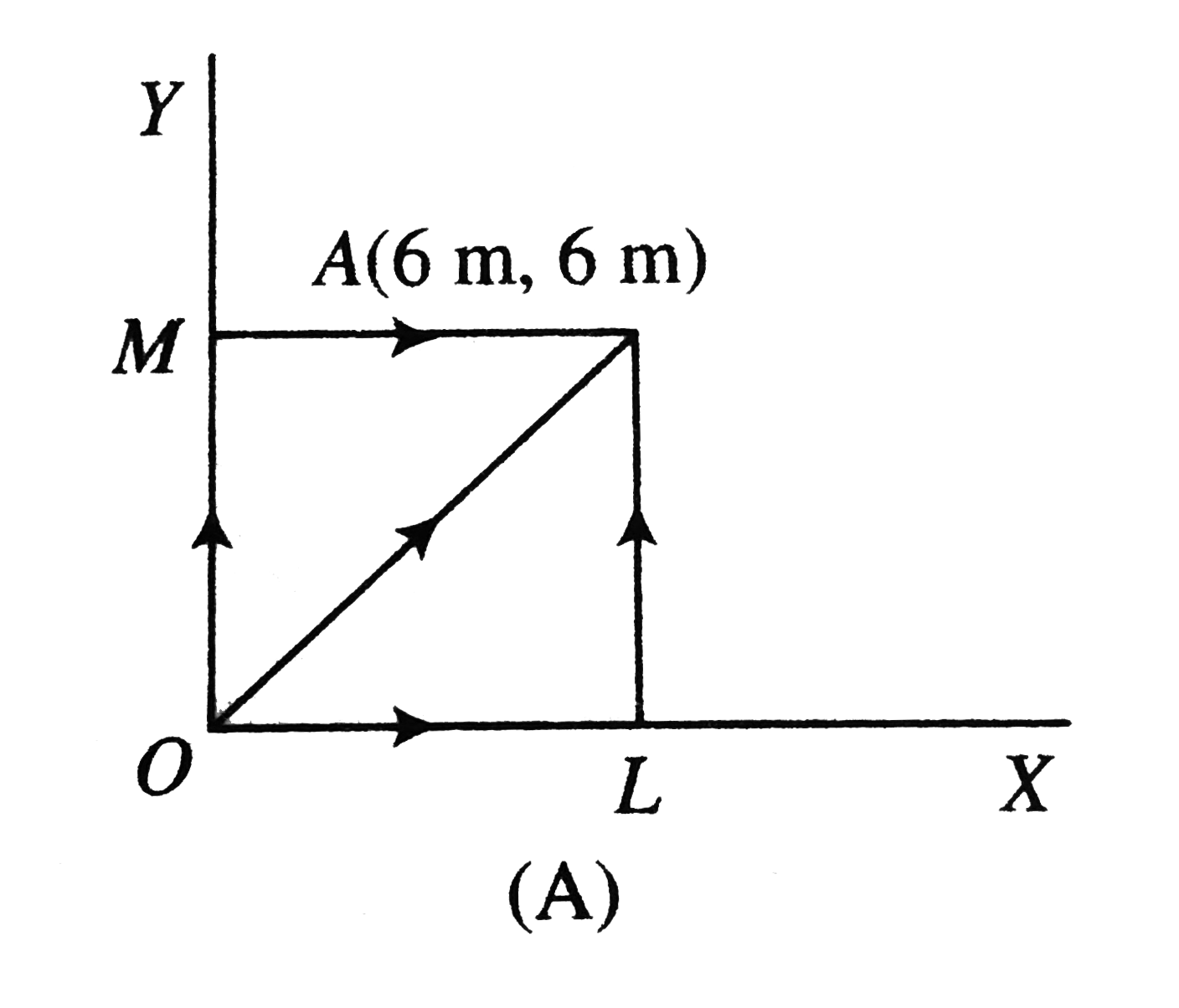
If the potential energy at O is
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity
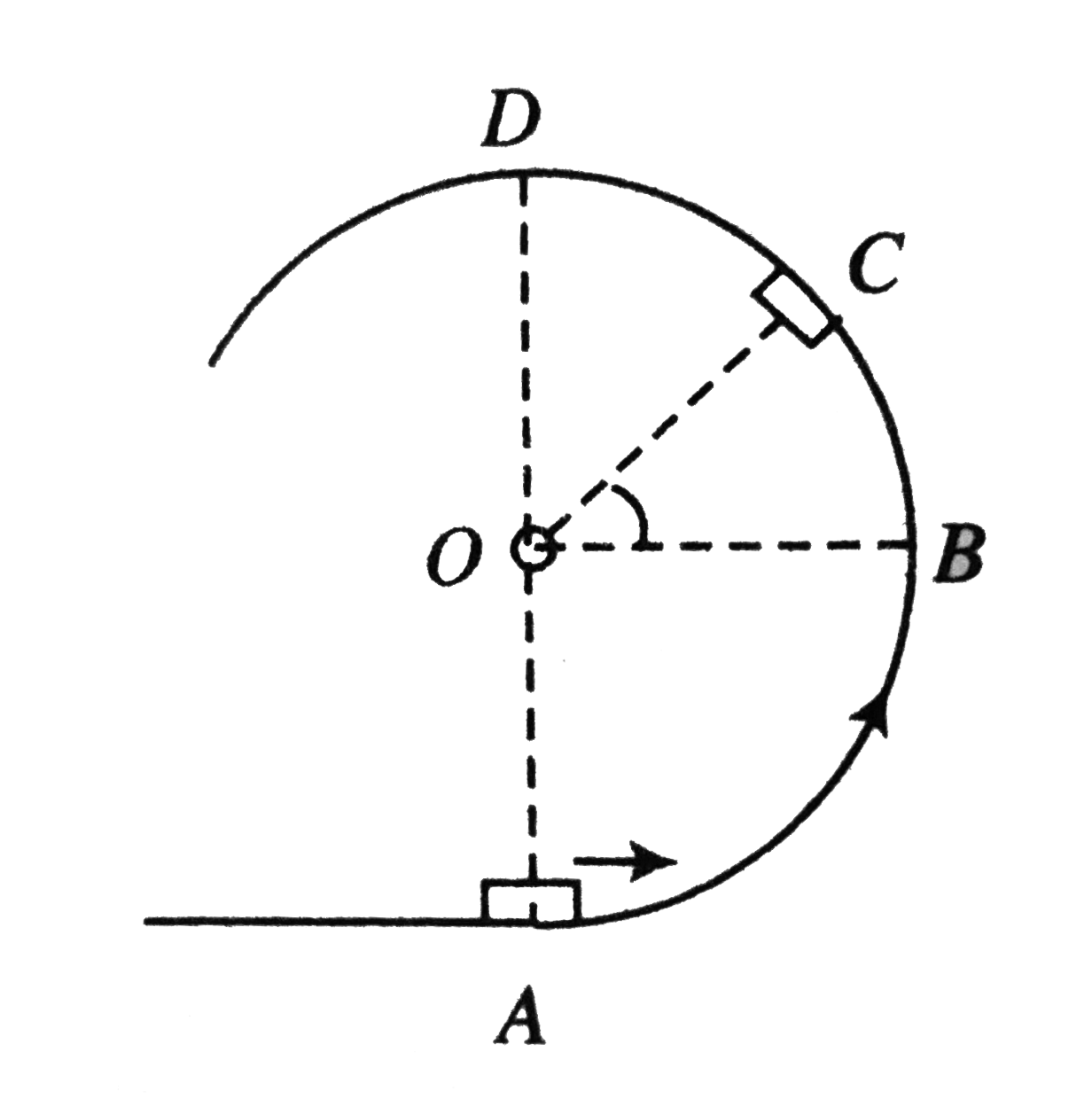
At what angle
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity

At what angle
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity
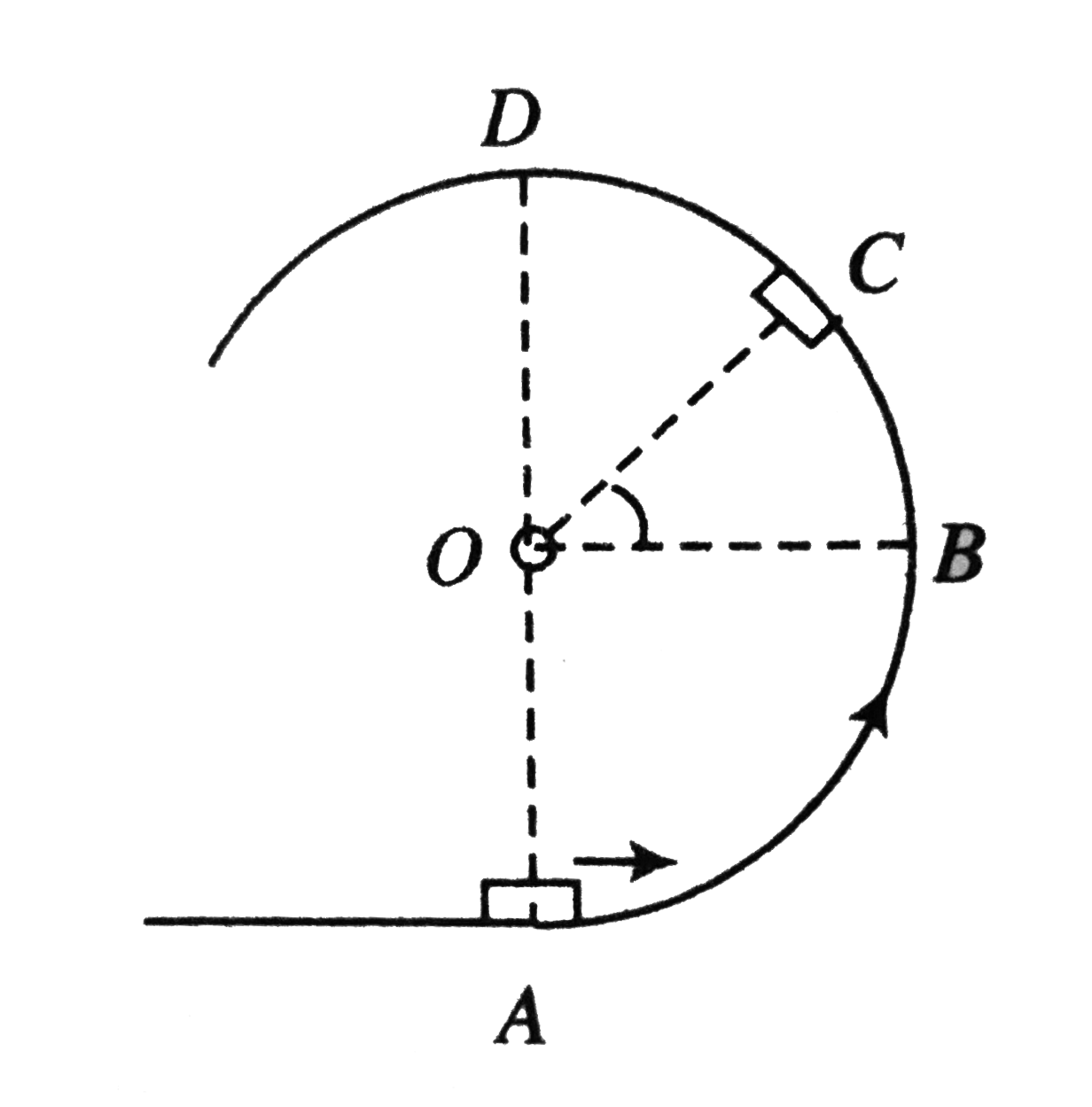
Find where the maximum contact force occurs between the block and the track.
View SolutionA force
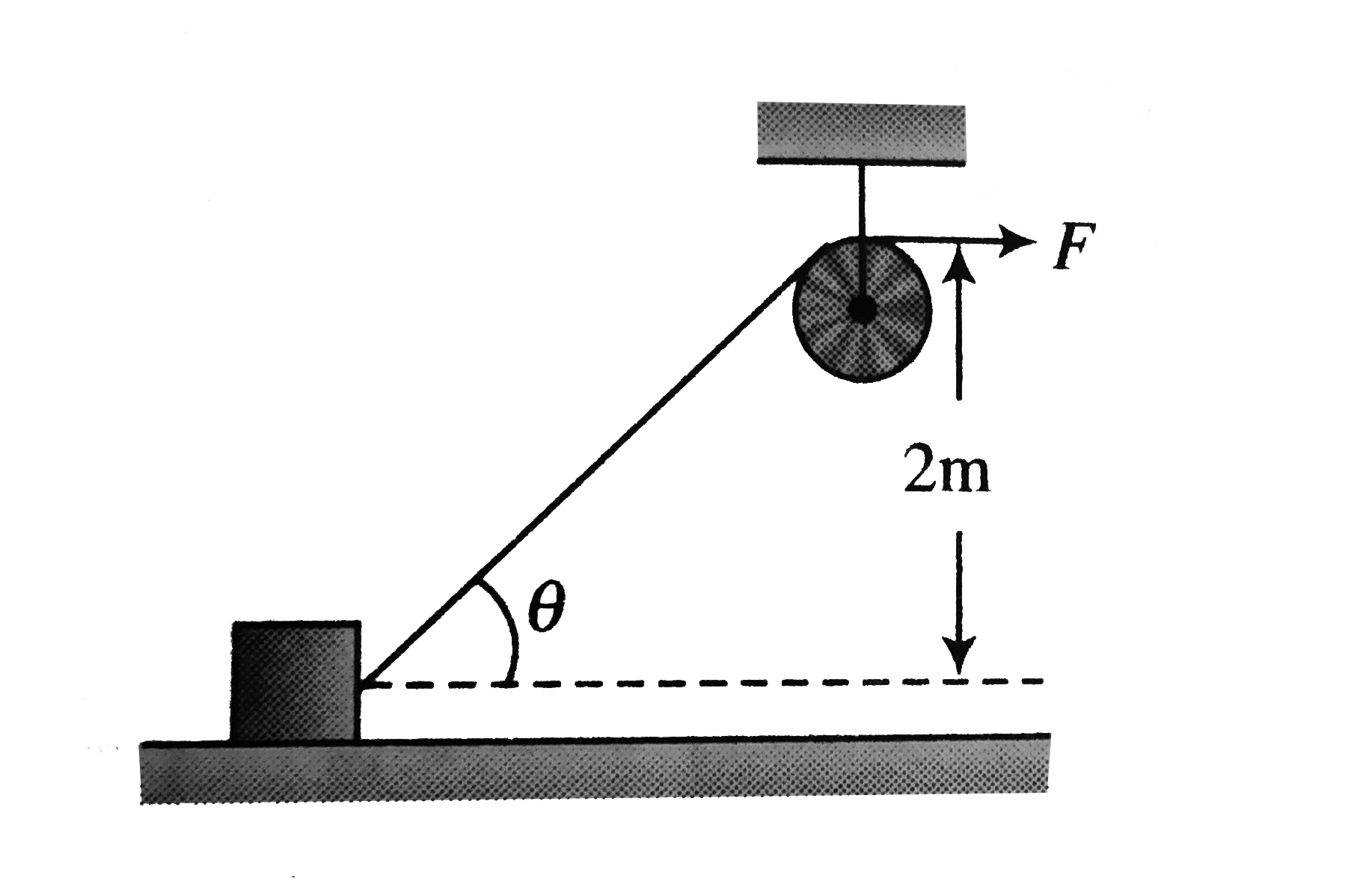
Net work done by the force F on the block is
View SolutionA force
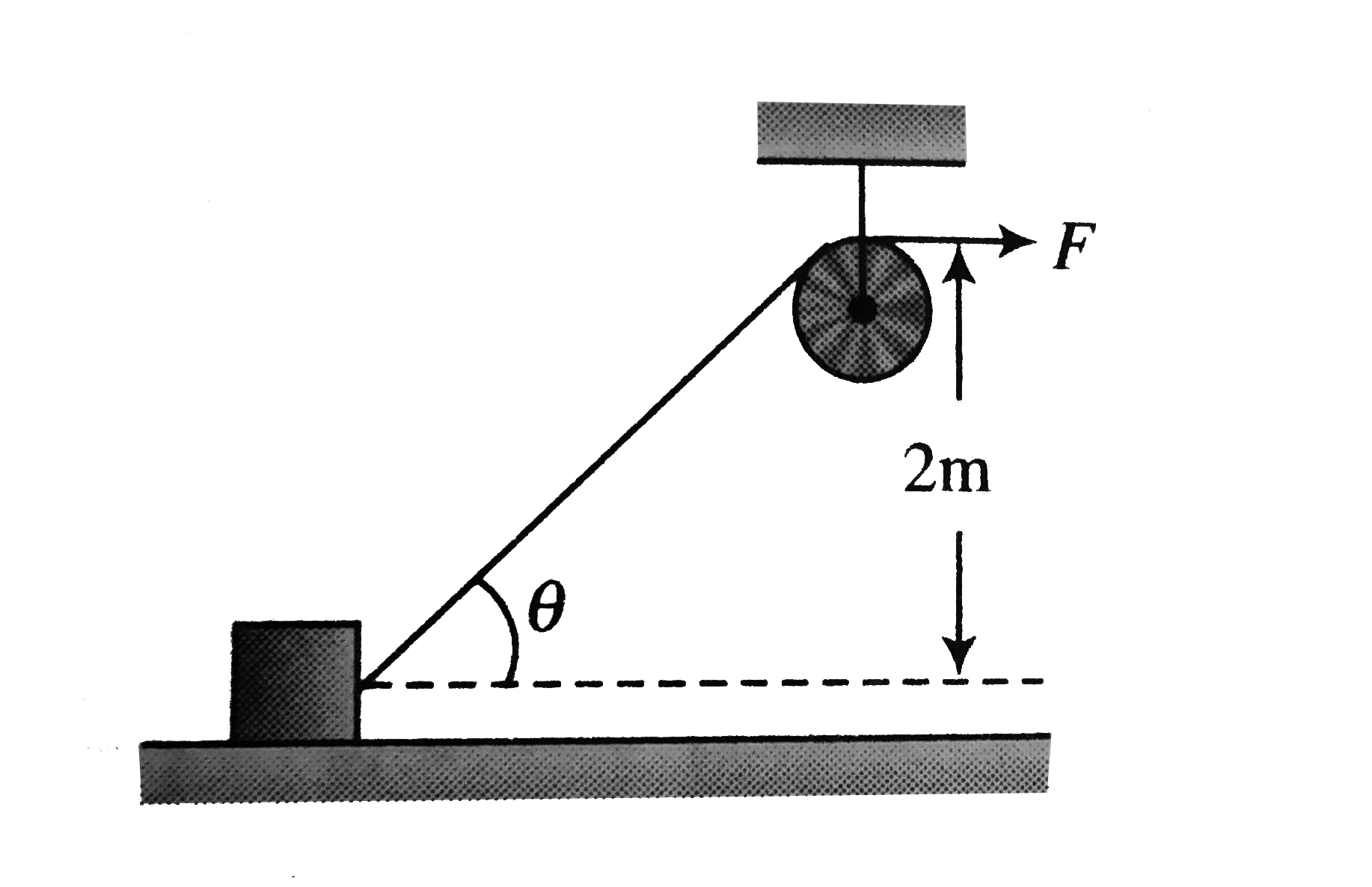
What is the final velocity of the block if initially it was at rest?
View SolutionA force
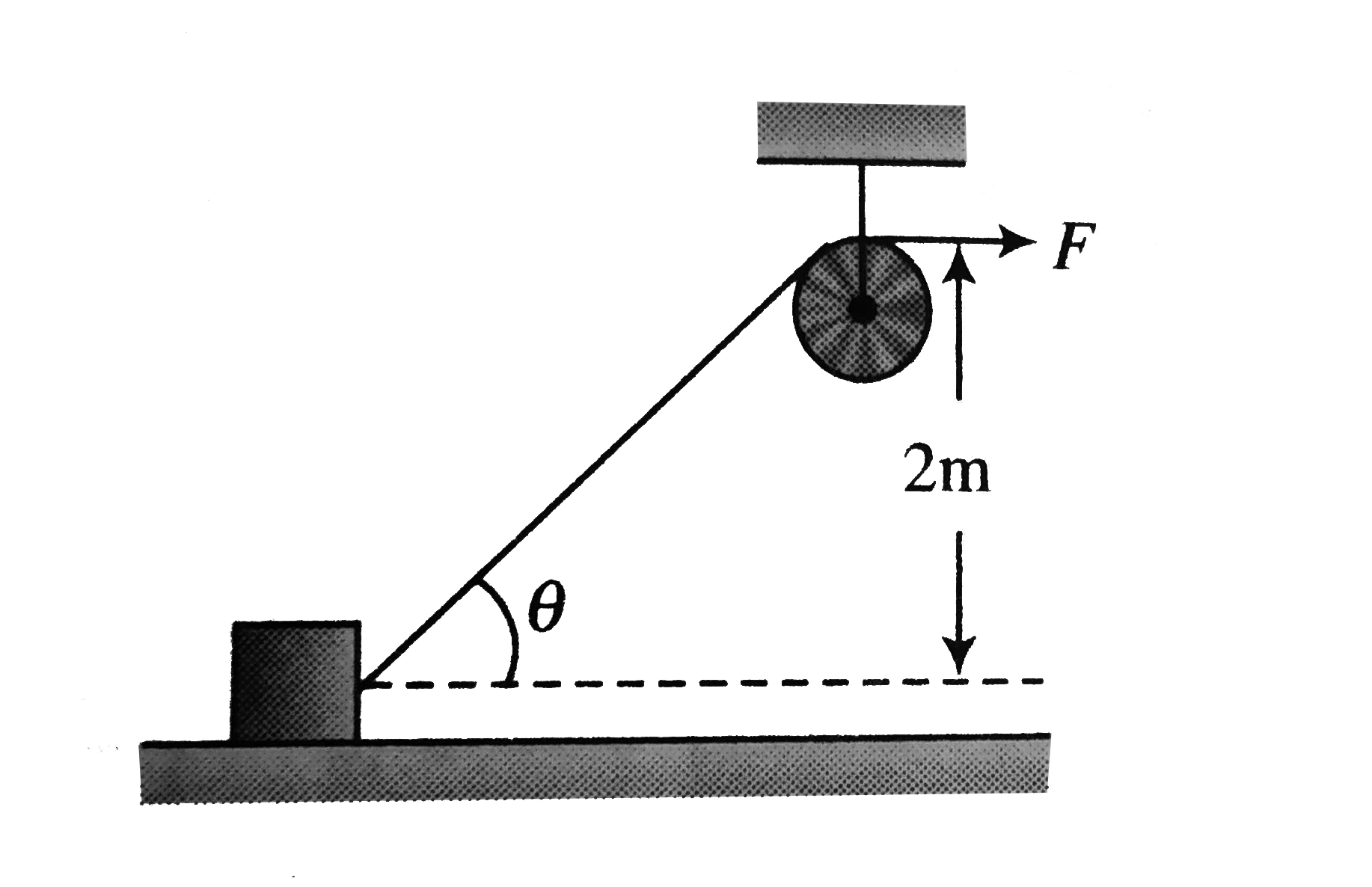
Find the ratio of initial acceleration to final acceleration of the block
View Solution
Linked Comprehension questions and complete solutions for chapter WORK, POWER & ENERGY of CENGAGE PHYSICS (HINGLISH) of Class 11