Complete Solutions to Single Correct of chapter WORK, POWER & ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, POWER & ENERGY |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The displacement x in meter of a particle of mass
View SolutionA mass M is lowered with the help of a string by a distance h at a distance acceleration
View SolutionA force of
View SolutionTwo identical
View SolutionIf we shift a body in equilibrium from A to C in a gravitational field via path AC or ABC,

View SolutionIn which of the following cases can the work done increase the potential energy?
View SolutionWork done by the conservative force on a system is equal to :
View SolutionWhich of the following statements is correct?
View SolutionA man
View SolutionAn engine pumps up
View SolutionA pump motor is used to deliver water at a certain rate from a given pipe. To obtain 'n' times water from the same pipe in the same time by what amount (a) the force and (b) power of the motor should be increased ?
View SolutionAn engine pumps water continously through a hose. Water leave the hose with a velocity
View SolutionA bus can be stopped by applying a retarding force F when it is moving with speed v on a level road. The distance covered by it before coming to rest is
View SolutionA heavy weight is suspended from a spring . A person raises the weight till the spring becomes slack . The done by him is
View SolutionThe speed v reached by a car of mass m in travelling a distance x, driven with constant power P, is given by
View SolutionPower supplied to a mass
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is

View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time
View SolutionA car drives along a straight level frictionless road by an engine delivering constant power. Then velocity is directly proportional to
View SolutionFigure shows the vertical section of a frictionless surface. A block of mass
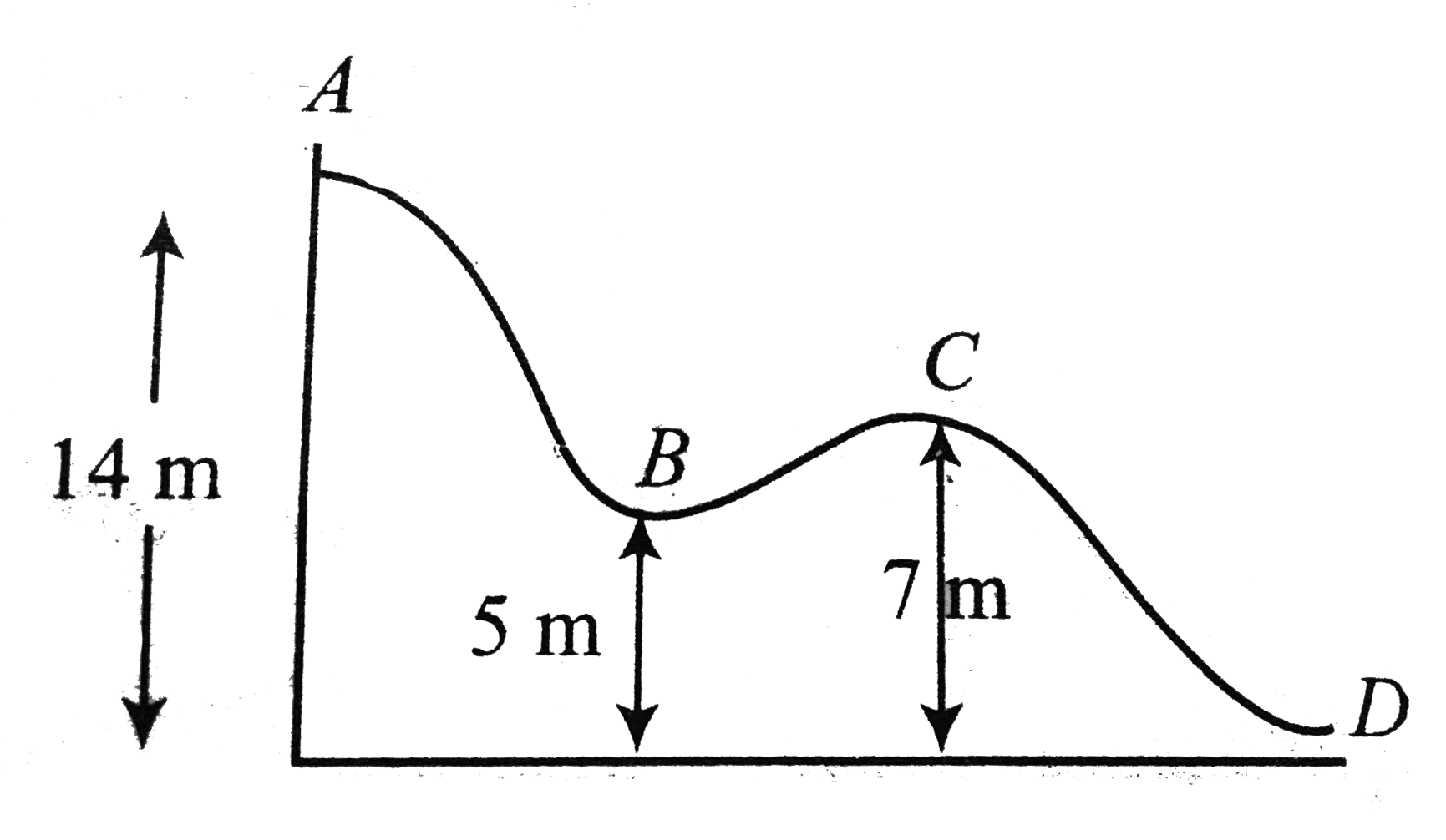
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as
View SolutionA particle of mass in is moving in a circular with of constant radius
View SolutionAn object of mass
View SolutionA toy gun a spring of force constant
View SolutionA block of
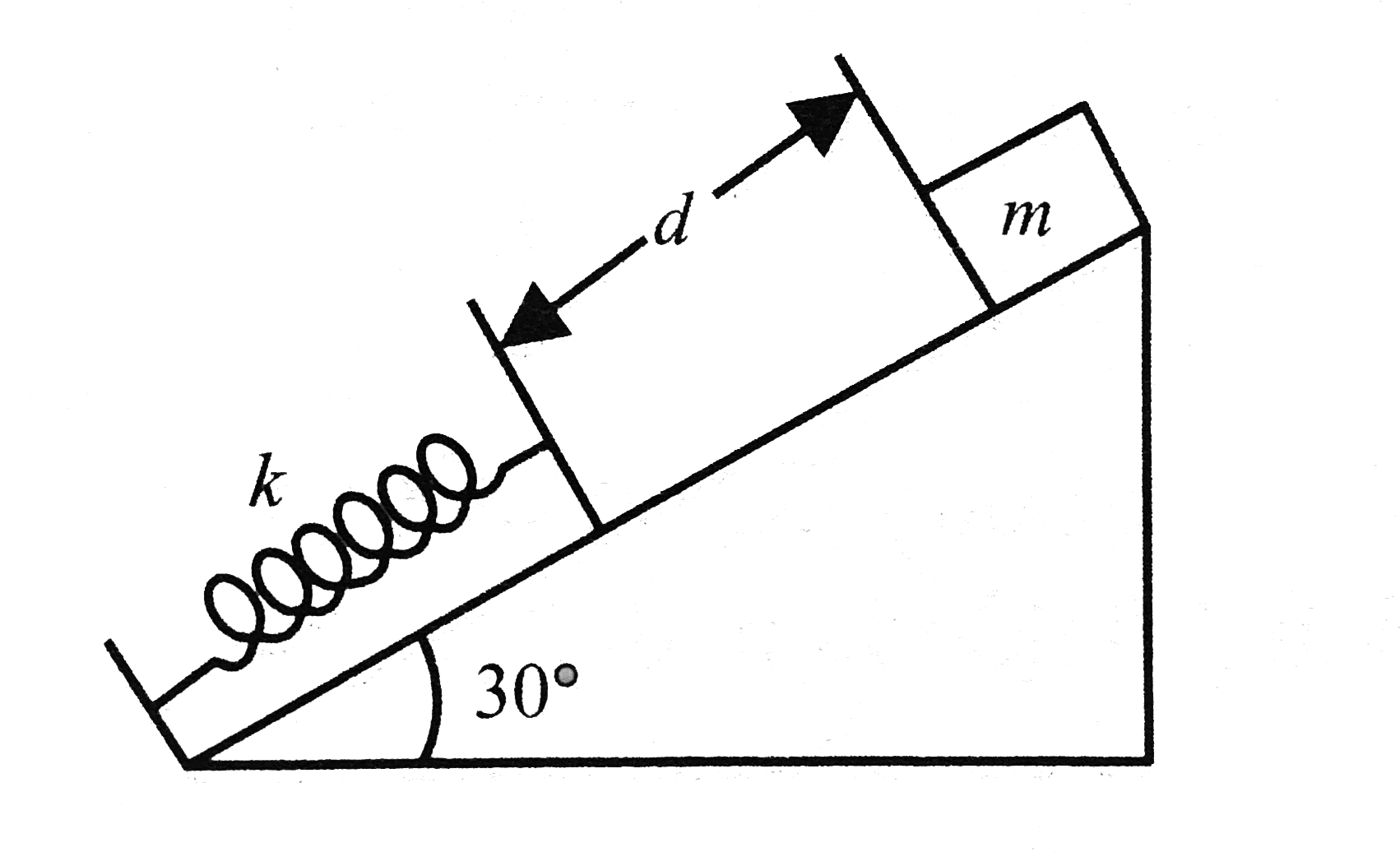
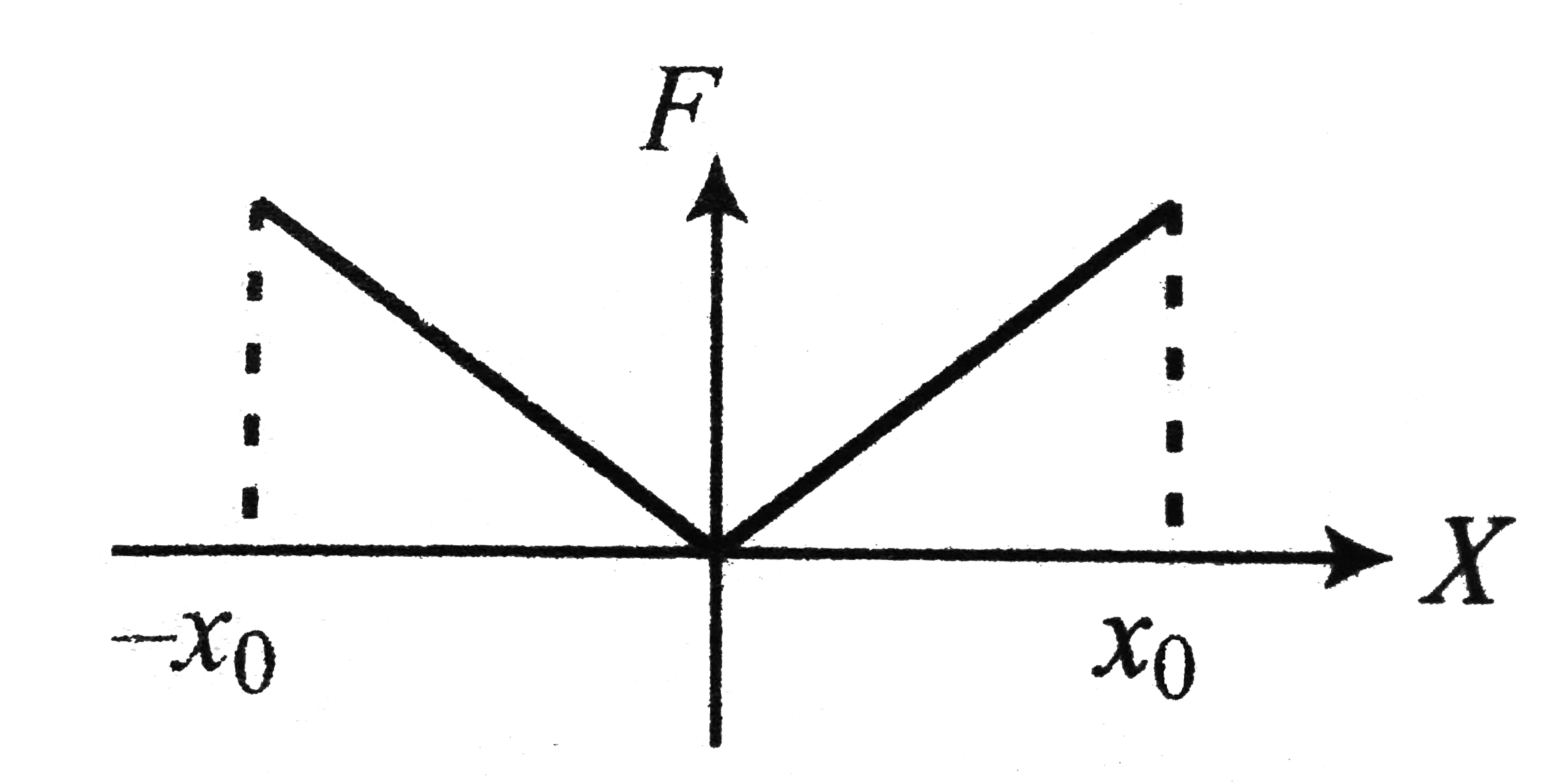
View SolutionFigure shows a plot of the conservative force F in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is
View SolutionA spring is compressed between two toy carts to masses
View SolutionA massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?
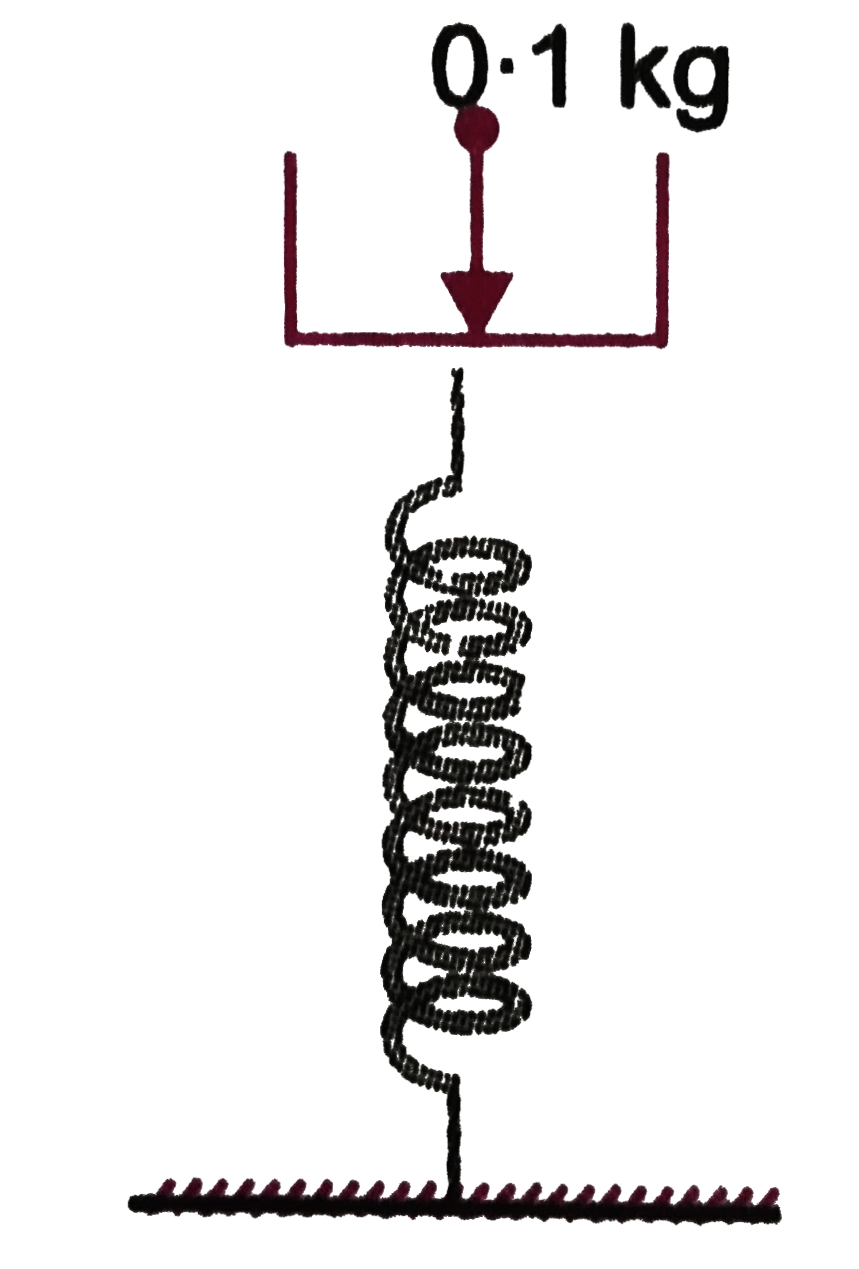
View SolutionA partical is realeased from the top of two inclined rought surface of height
View SolutionSystem shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of

View SolutionWhen a person stands on a weighing balance, working on the principle of Hooke's law, it shows a reading of
View SolutionA particle of mass
View SolutionIn the above question, the average power delivered by gravity is
View SolutionA person of mass
View SolutionA particle located in a one-dimensional potential field has its potential energy function as
View SolutionA large slab of mass

View SolutionA small block of mass
View SolutionA particle of mass
View SolutionA particle of mass m moves along a circular path of radius r with a centripetal acceleration
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius

View SolutionTwo discs, each having mass
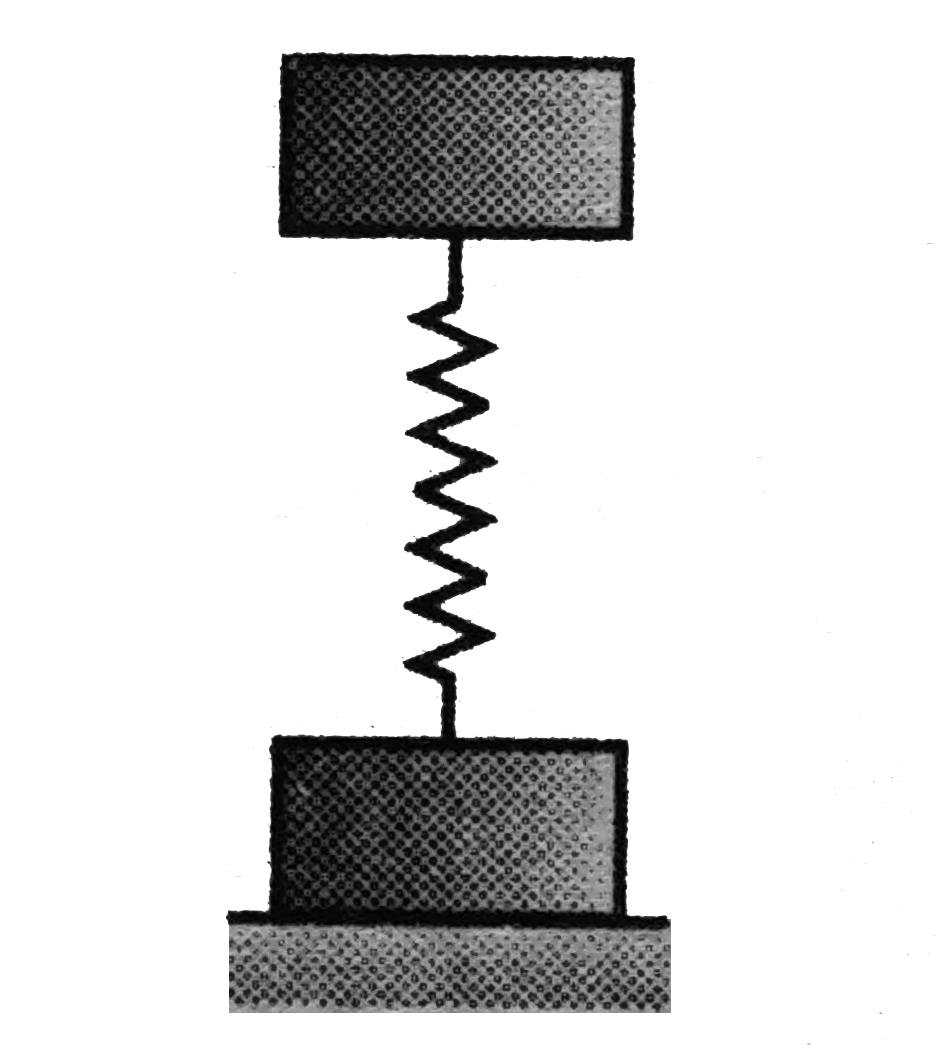
View SolutionTwo ends A and B of a smooth chain of mass
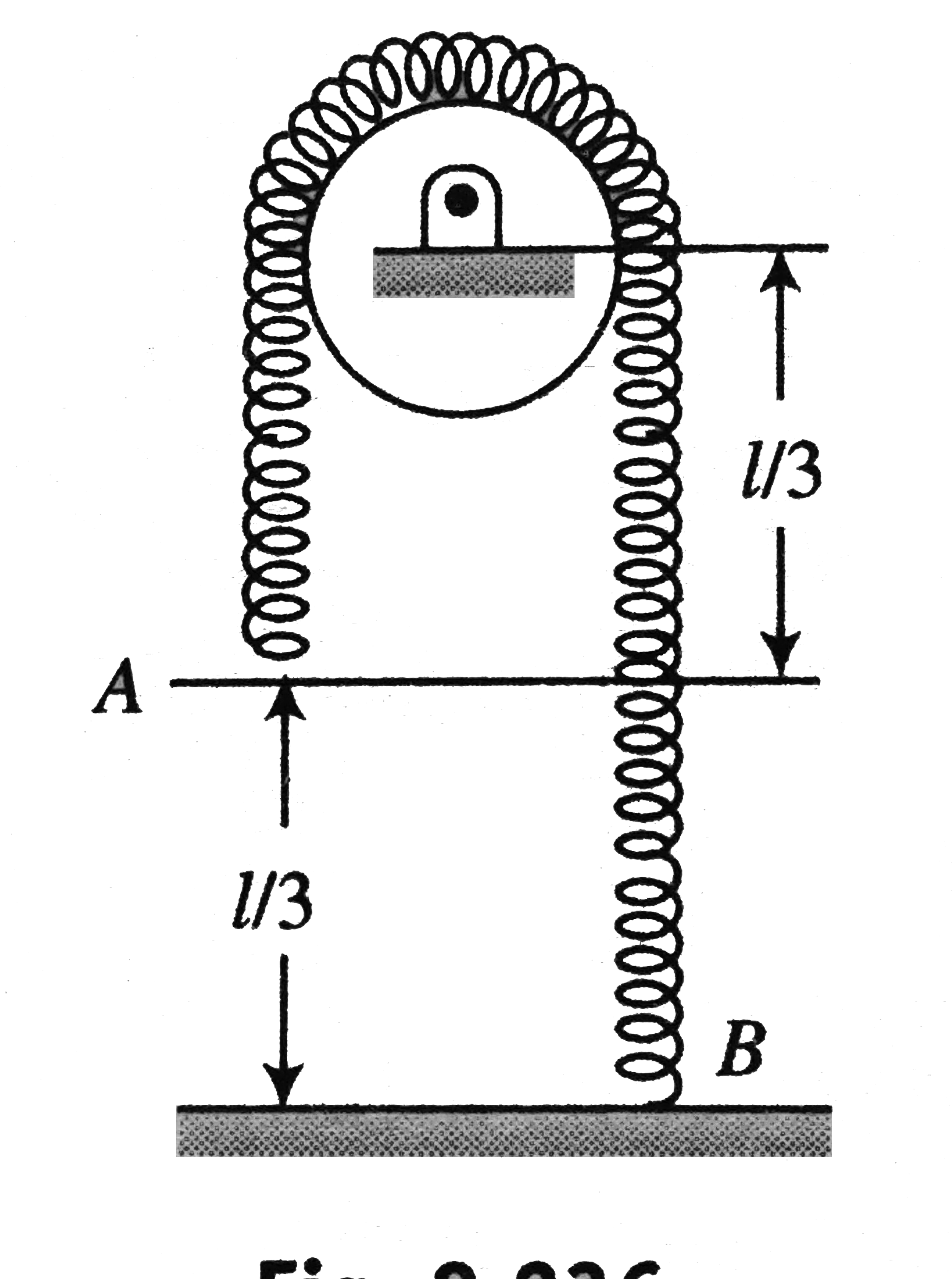
View SolutionA block

i. Normal reaction performs positive work on the block.
ii. Frictional work done on the block is negative.
iii. No net work is done by normal reaction and friction on the block.
Now mark the correct answer.
View SolutionA man places a chain (of mass
View SolutionThe potential energy of a particle of mass
View SolutionThe blocks A and B shown in figure have masses
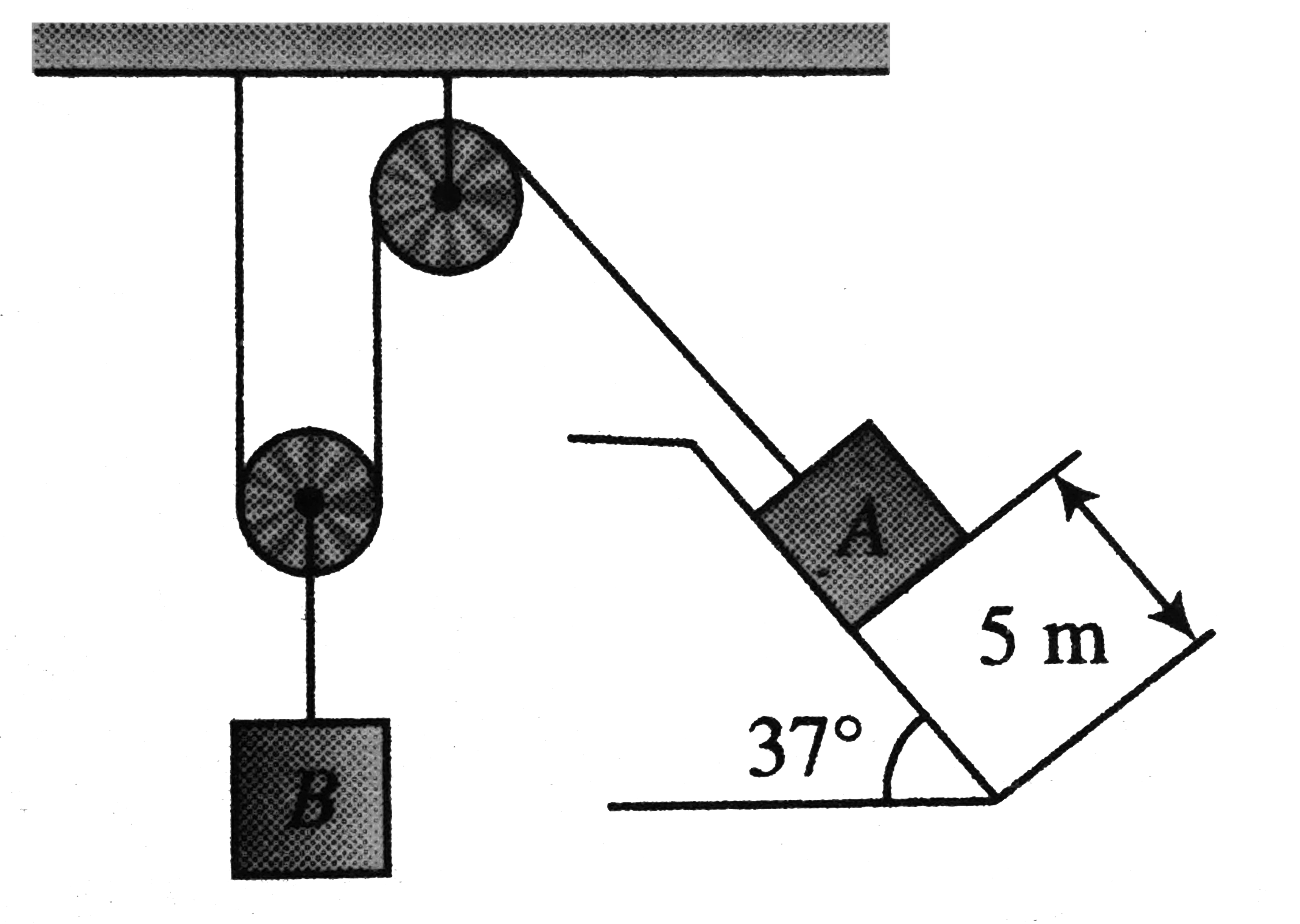
View SolutionA collar B of mass
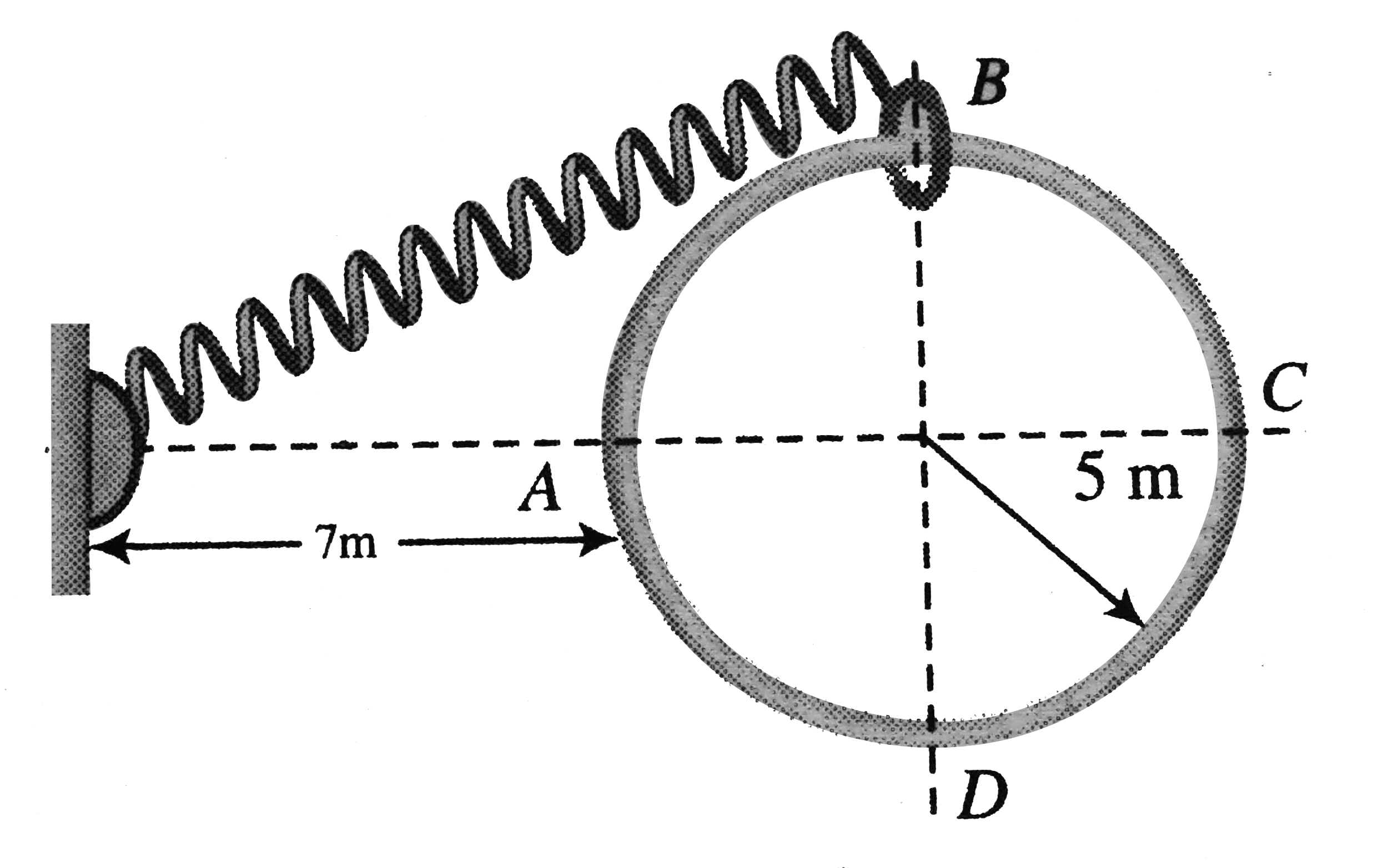
View SolutionA block attached to a spring, pulled by a constant horizontal force, is kept on a smooth surface as shown in figure. Initially, the spring is in the natural length state. Then the maximum positive work that the applied force F can do is (give that string does not break)

View SolutionA particle is projected along a horizontal field whose coefficient of friction varies as
View SolutionTwo identical blocks A and B are placed on two inclined planes as shown in figure. Neglect resistance and other friction.
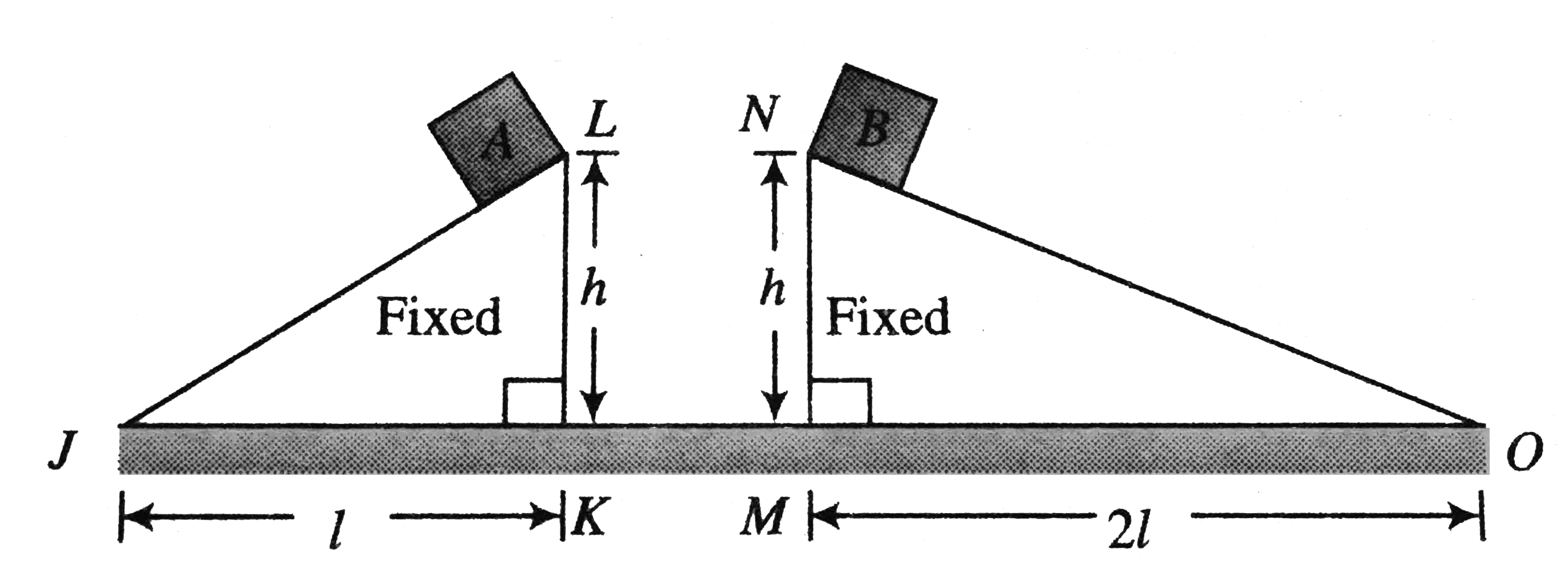
Read the following statements and choose options.
Statement I: The kinetic energy of A on sliding to J will be greater than the kinetic of B on sliding to O.
Statement II: The acceleration of A will be greater than acceleration of B when both are released on the inclined plane.
Statement III: The work done by external agent to move the block slowly from position B to O is negative.
View SolutionA block of mass
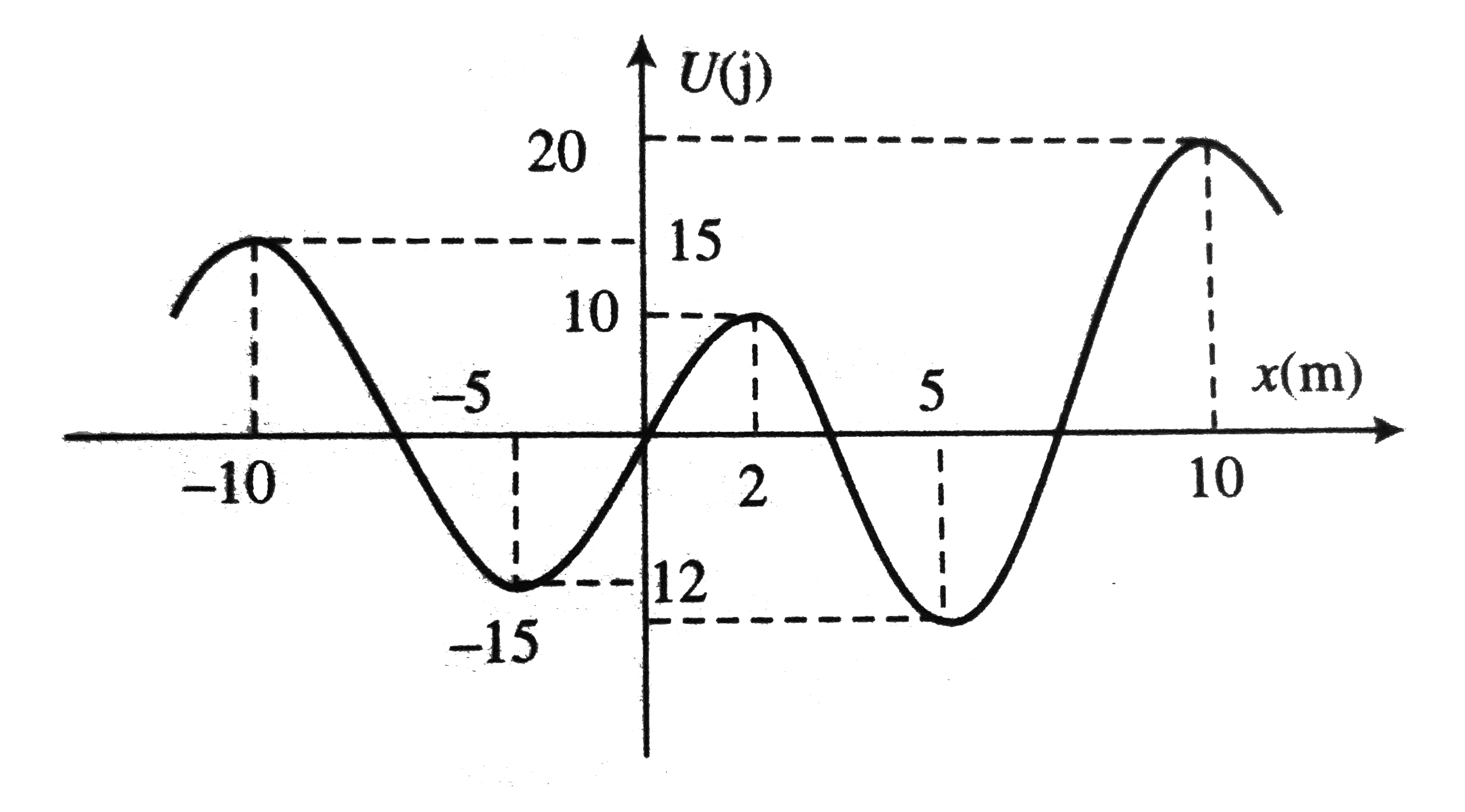
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,

View SolutionOne end of an unstretched vertical spring is attached to the ceiling and an object attached to the other end is slowly lowered to its equilibrium position. If S is the gain in spring energy and G is the loss in gravitational potential energy in the process, then
View SolutionThe potential energy function associated with the force
View SolutionThe potential energy for a force filed
View SolutionA particle is projected with a velocity
View SolutionA block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is
 .
.
View SolutionIn the above question, the maximum power delivered by the agent in pulling up the rope is
View SolutionA particle A of mass

View SolutionA particle is projected vertically upwards with a speed of
View SolutionAn engine can pull four coaches at a maximum speed of
View SolutionIn figure, the variation of potential energy of a particle of mass
View SolutionBlock
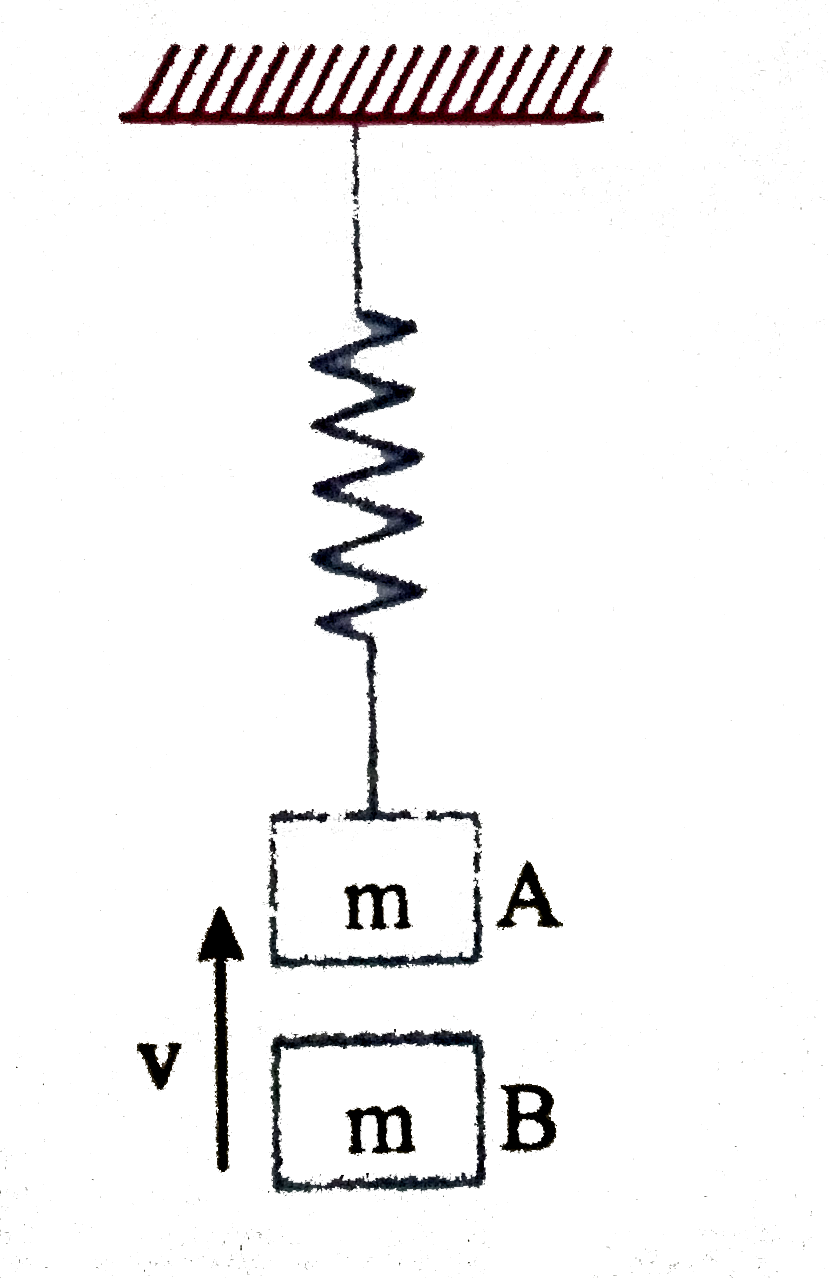
View SolutionA machine delivers power to a body which is proportional to velocity of the body. If the body starts with a velocity which is almost negligible, then the distance covered by the body is proportional to
View SolutionThe kinetic energy acquired by a mass
View SolutionA particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is

View SolutionA projectile is fired with some velocity making certain angle with the horizontal. Which of the following graphs is the best representation for the kinetic energy of a projectile (KE) versus its horizontal displacement(x)?
View SolutionTwo constant forces
View SolutionGiven
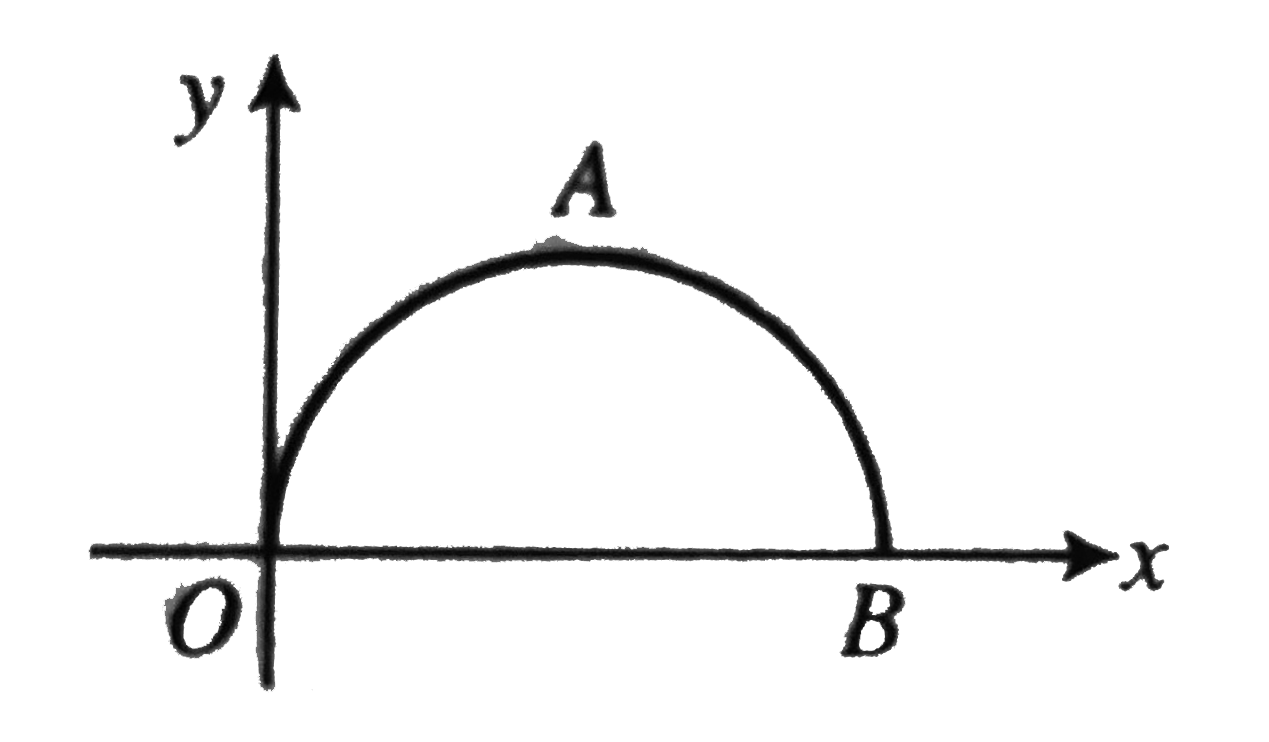
View SolutionA force
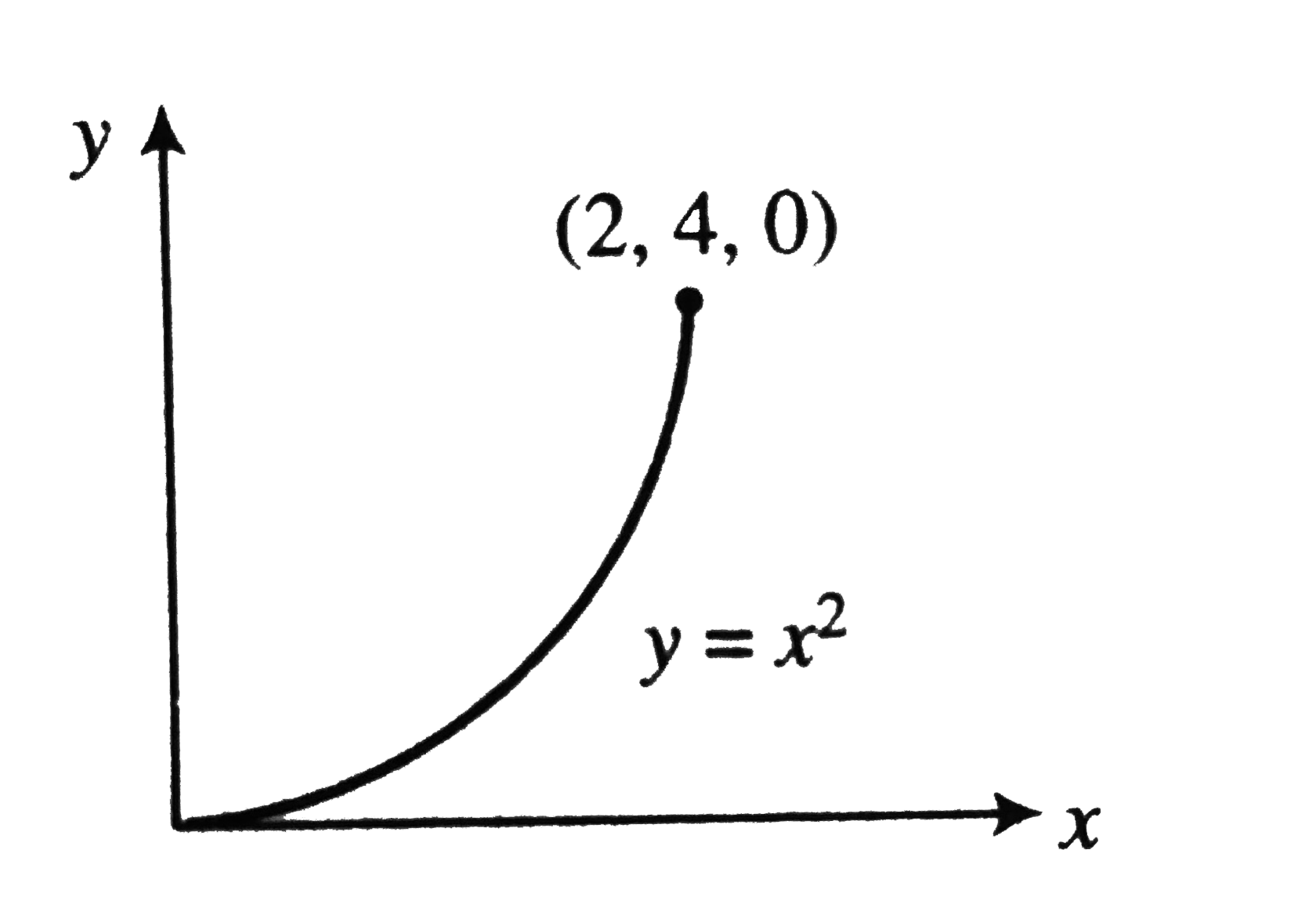
View SolutionThe potential energy of a particle is determined by the expression
View SolutionIn the position shown in figure, the spring is at its natural length. The block of mass
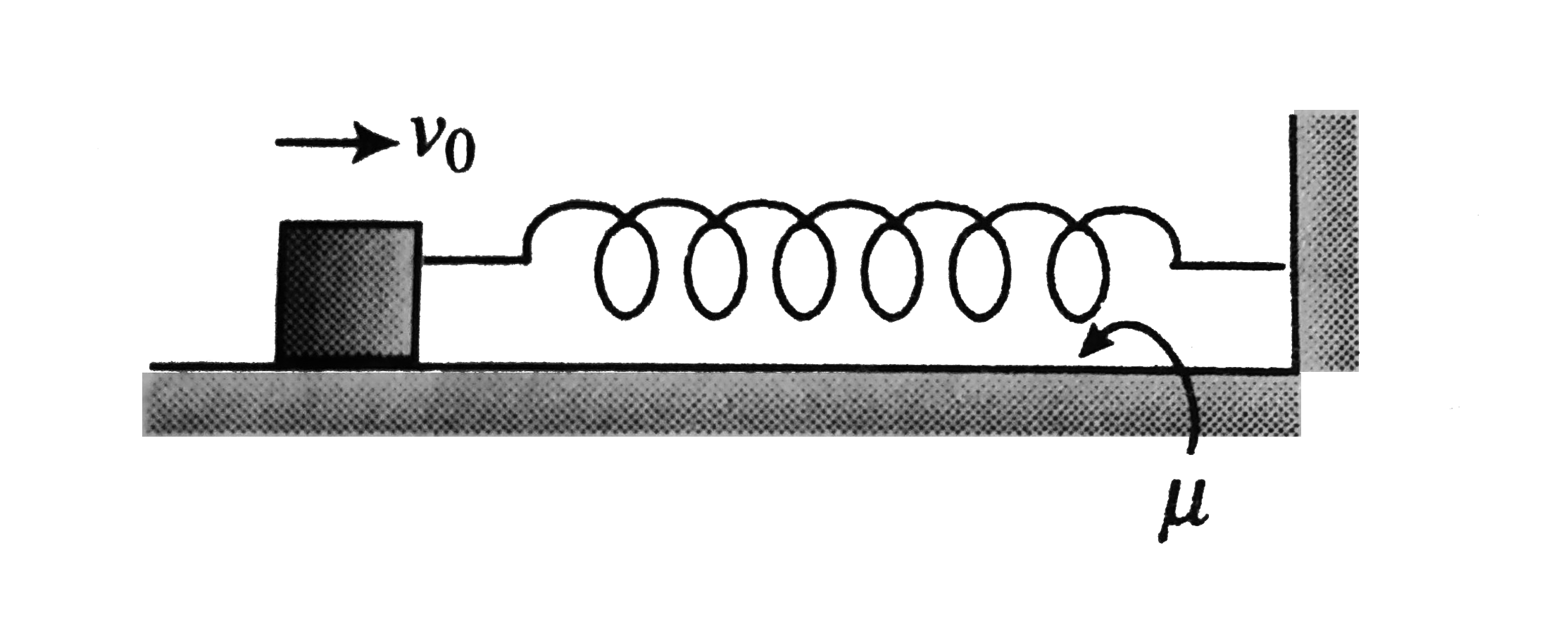
View SolutionIn the figure shown, a spring of spring constant
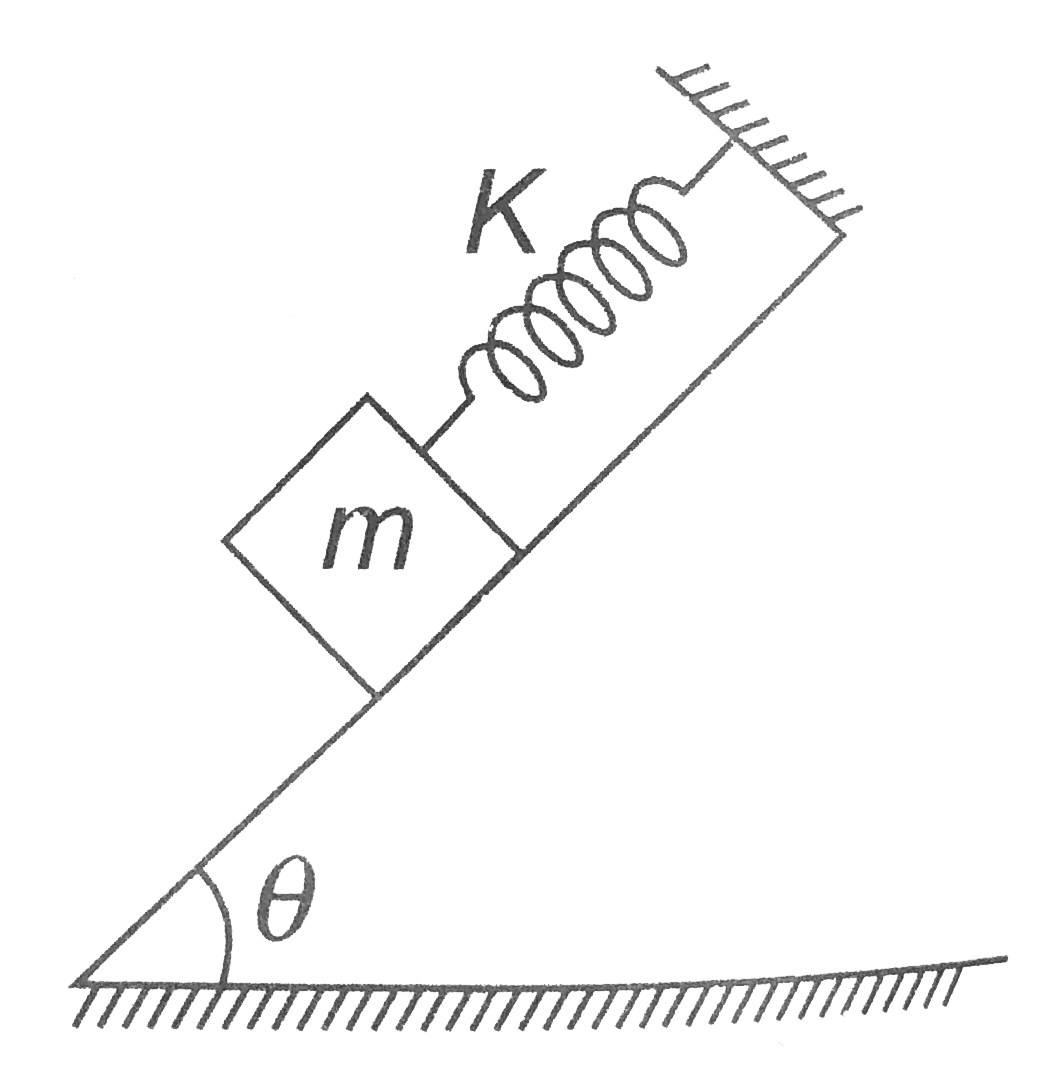
View SolutionLet
View SolutionA mass m starting from A reaches B of a frictionless track. On reaching B, it pushes the track with a force equal to x times its weight, then the applicable relation is
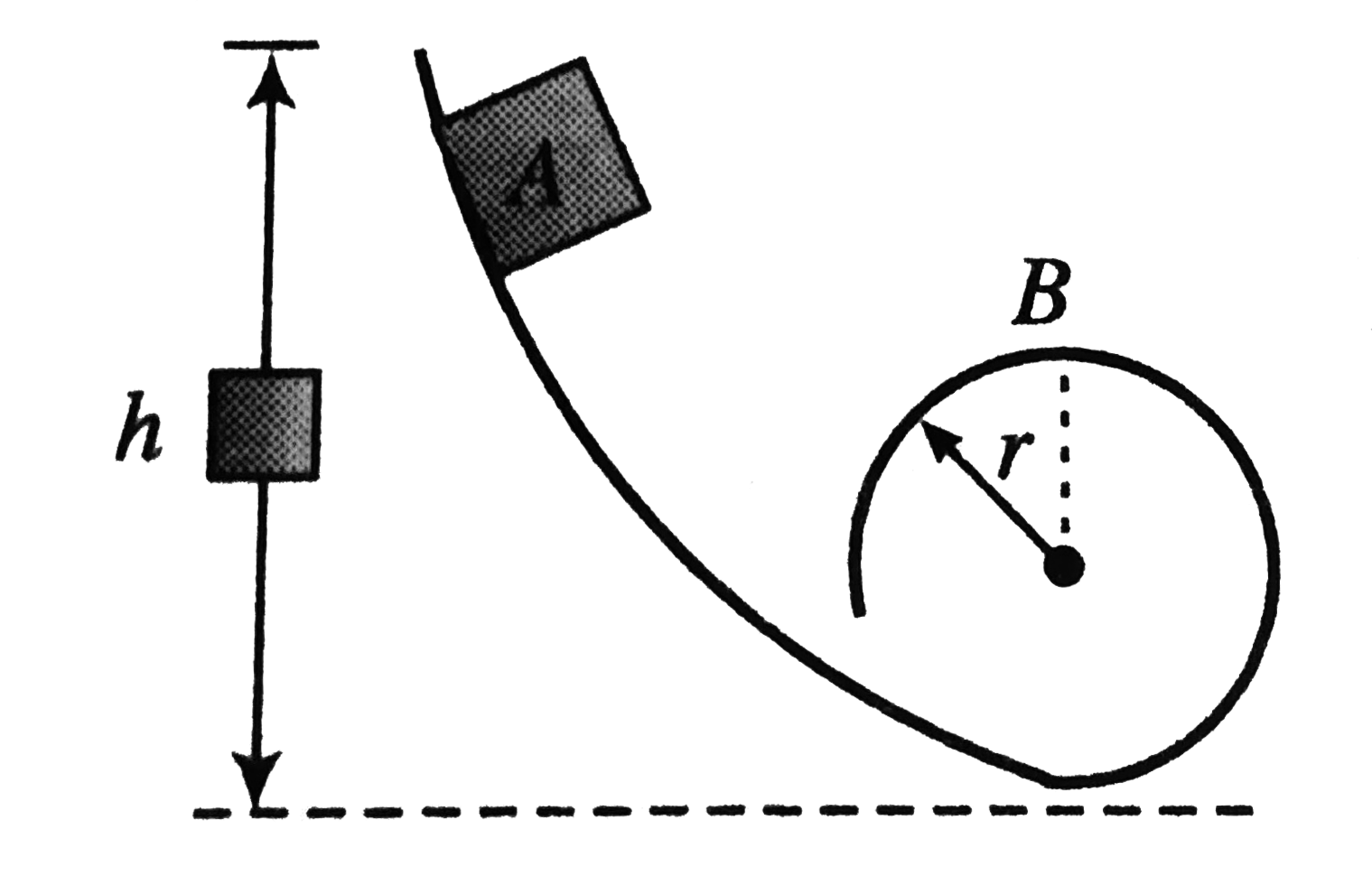
View SolutionA particle of mass
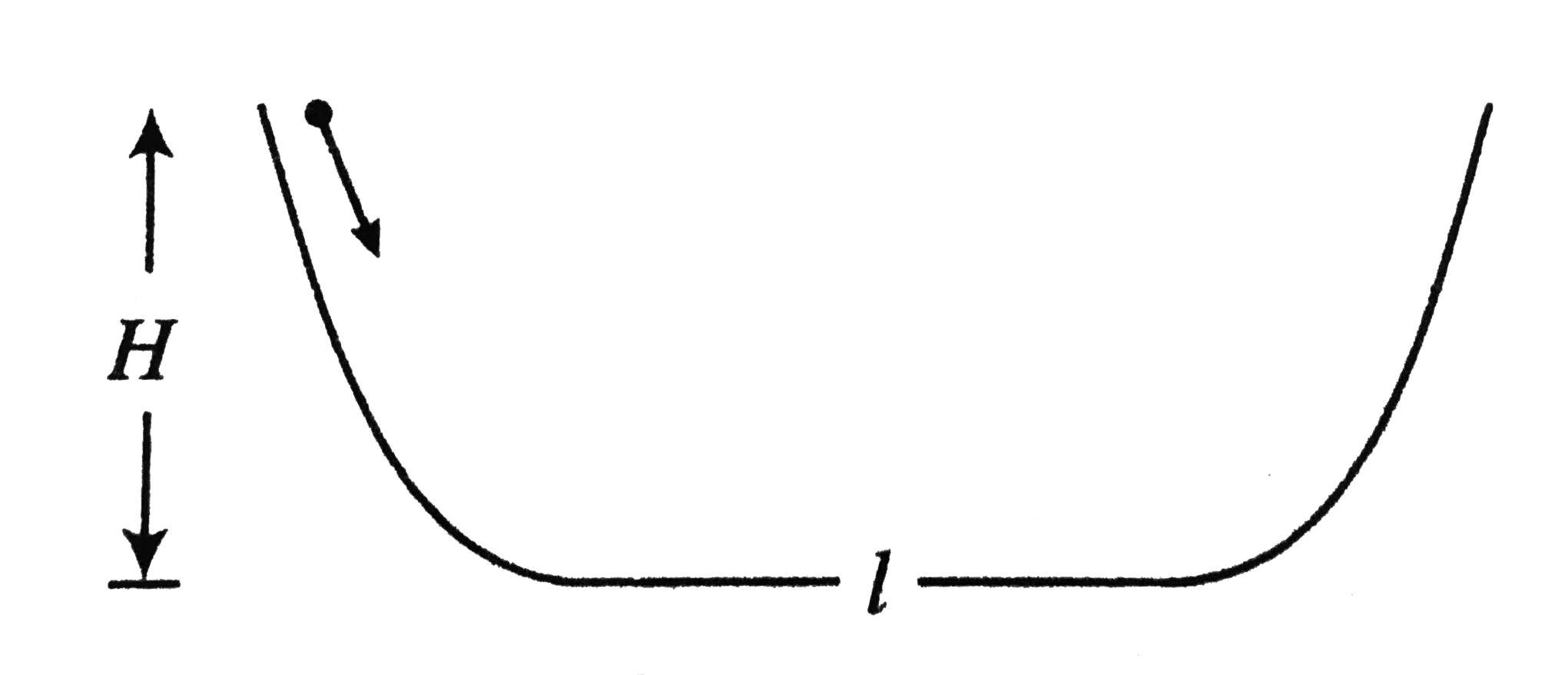
View SolutionA block of mass

View SolutionA moving railway compartment has a spring of constant k fixed to its front wall. A boy stretches this spring by distance x and in the mean time the compartment moves by a distance s. The work done by boy w.r.t. earth is

View SolutionA rope ladder of length L is attached to a balloon of mass M. As the man of mass m climbs the ladder into the balloon basket, the balloon comes down by a vertical distance s. Then the increase in potential energy of man divided by the increase in potential energy of balloon is
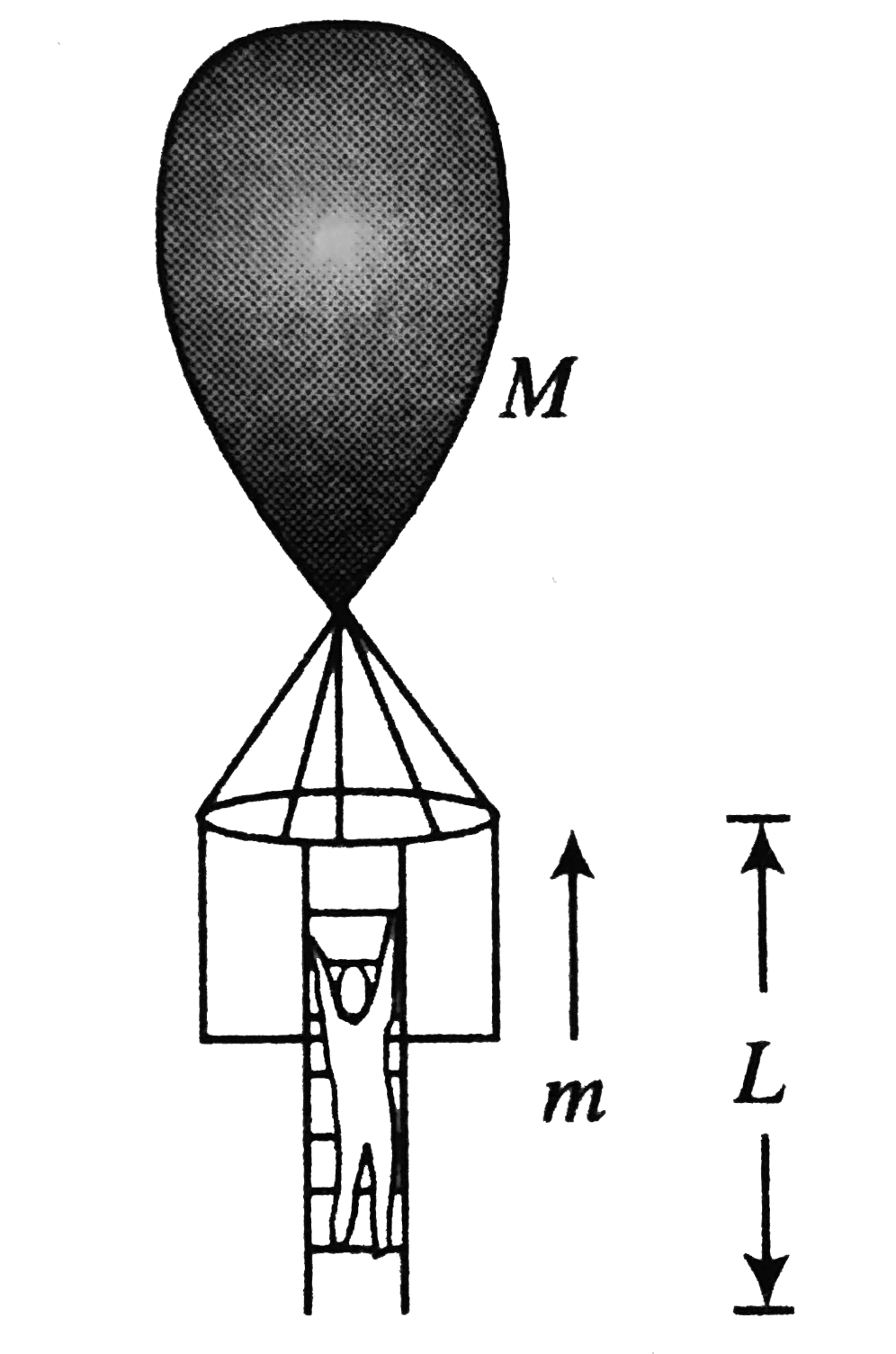
View SolutionA block of mass
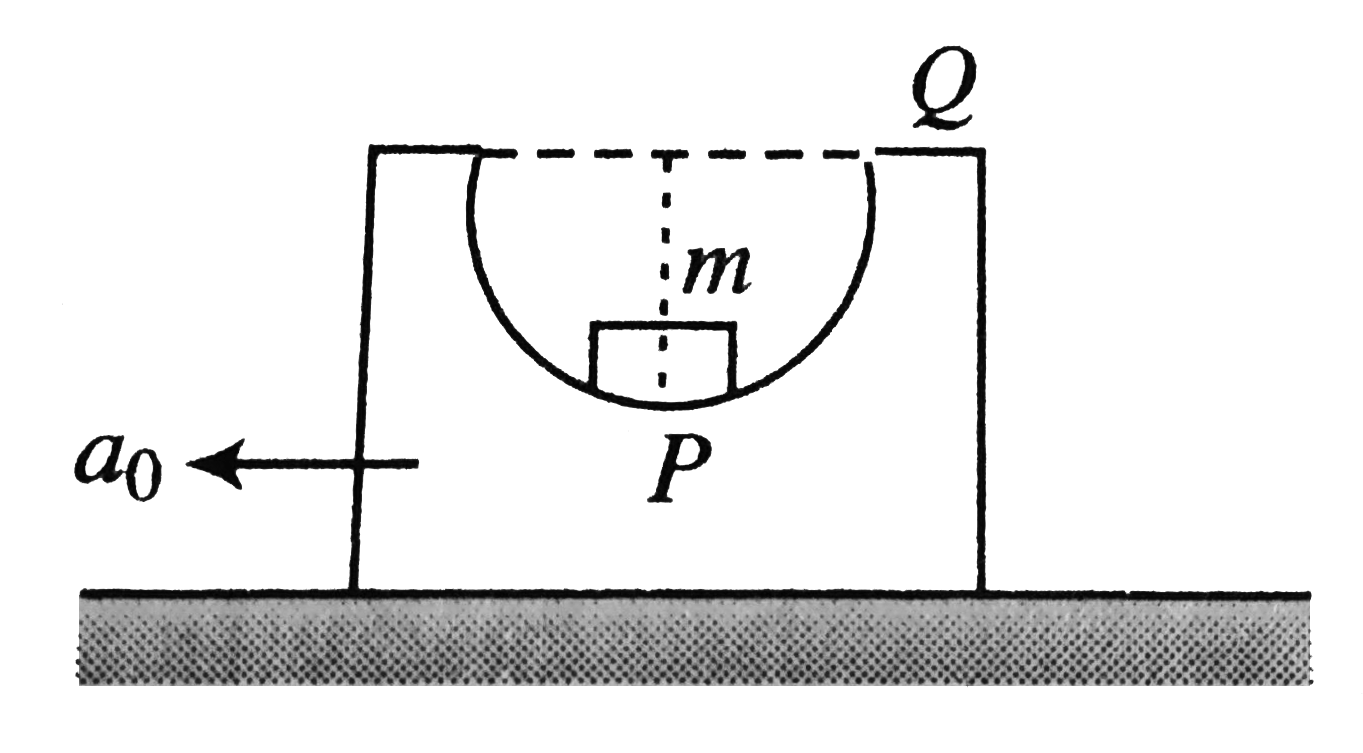
View SolutionFigure shows a smooth vertical circular track AB of radius R. A block slides along the surface AB when it is given a velocity equal to
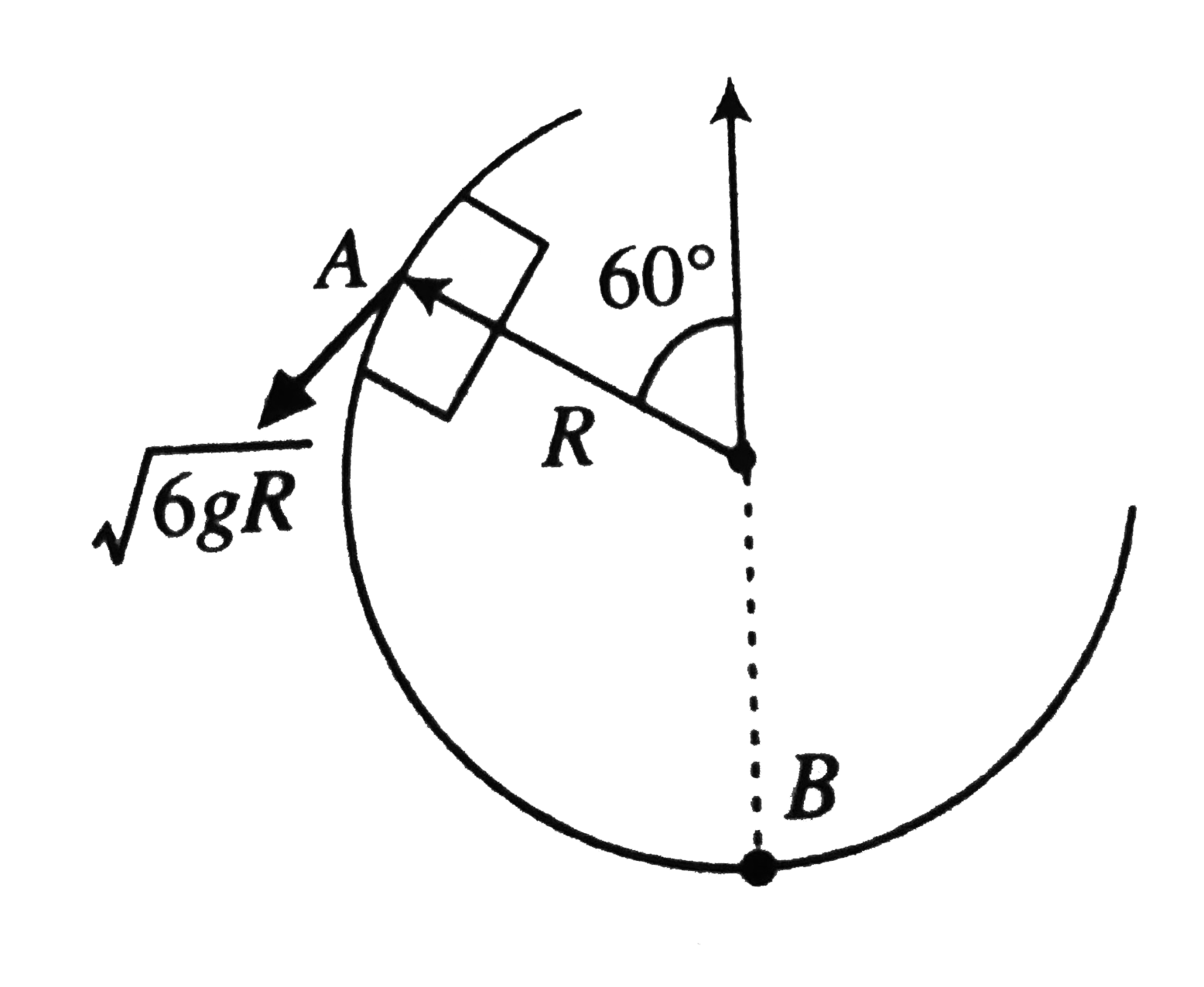
View SolutionA bead of mass m is released from rest at A to move along the fixed smooth circular track as shown in figure. The ratio of magnitudes of centripetal force and normal reaction by the track on the bead at any point

View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle

View SolutionTwo bodies of masses

View SolutionA
View SolutionTwo spring P and Q having stiffness constants
View SolutionIn the above question, if equal forces are applied on two springs, then
View SolutionWater is drawn from a well in a
View SolutionA bead of mass
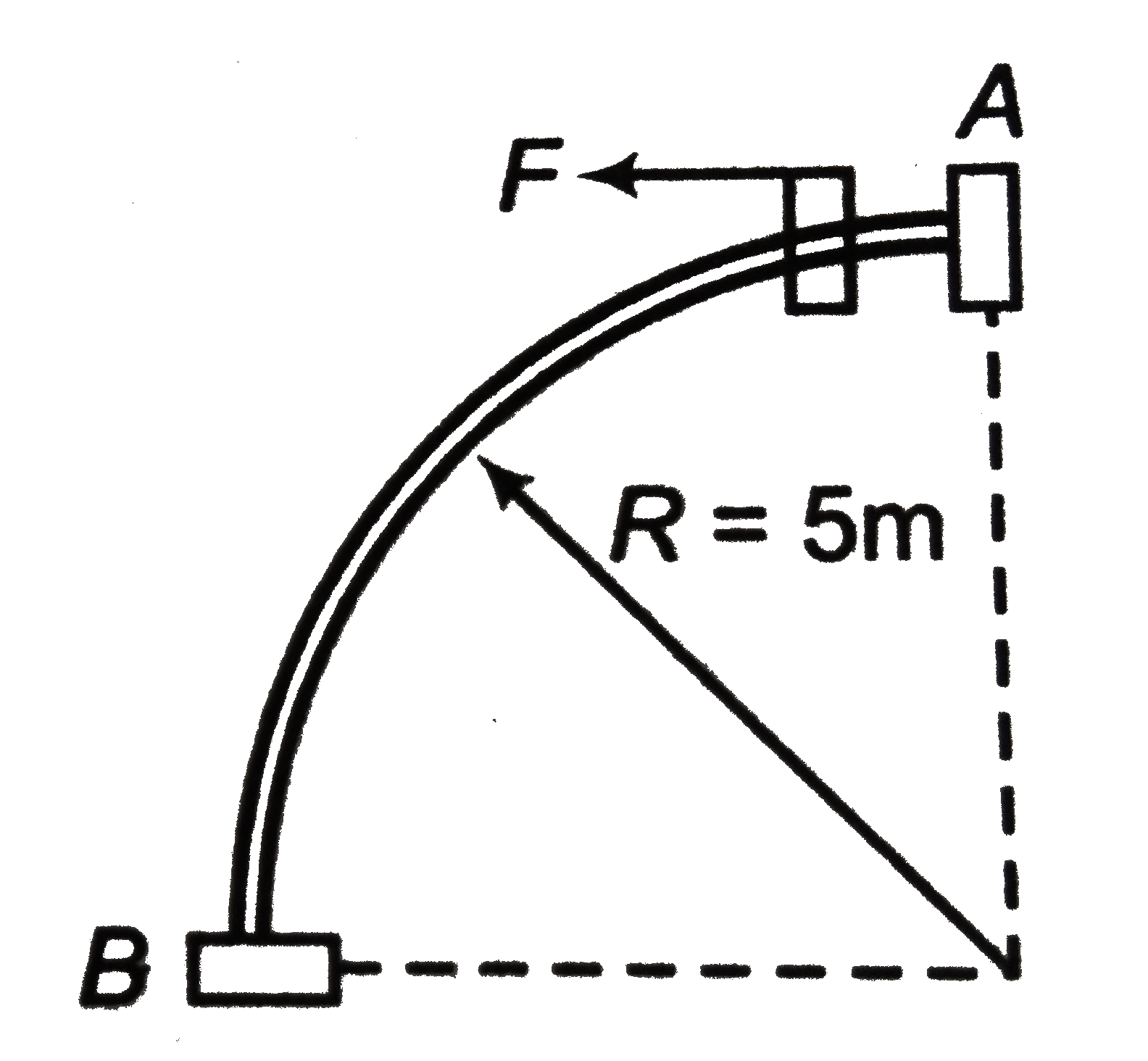
View SolutionA block of mass

View SolutionFigure shows a plot of the potential energy as a function of
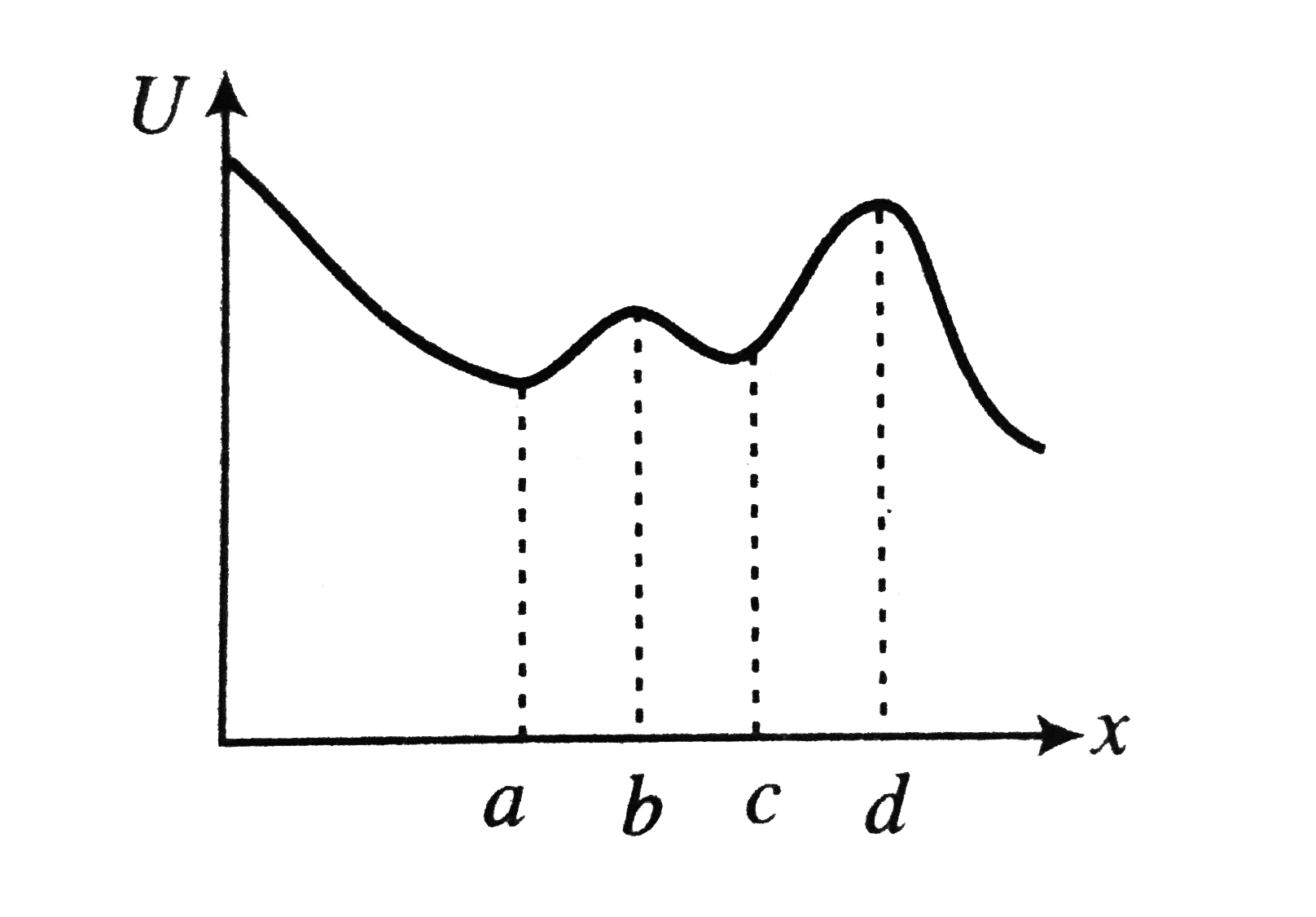
View SolutionA
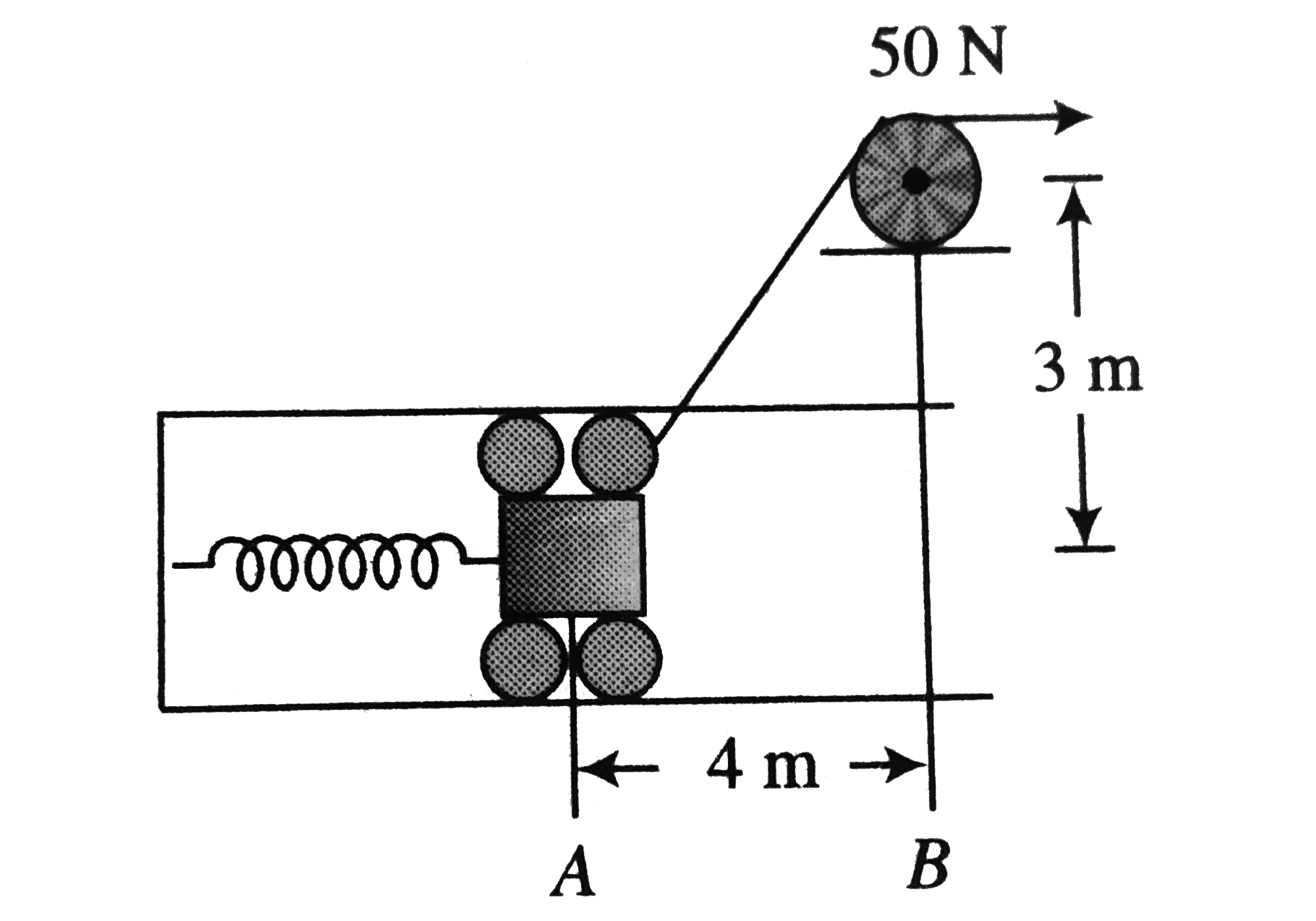
View SolutionTwo identical blocks, each having mass M, are placed as shown in figure. These two blocks A and B are smoothly conjugated, so that when another block C of mass m passes from A to B there is no jerk. All the surfaces are frictionless, and all three blocks are free to move. Block C is released from rest, then
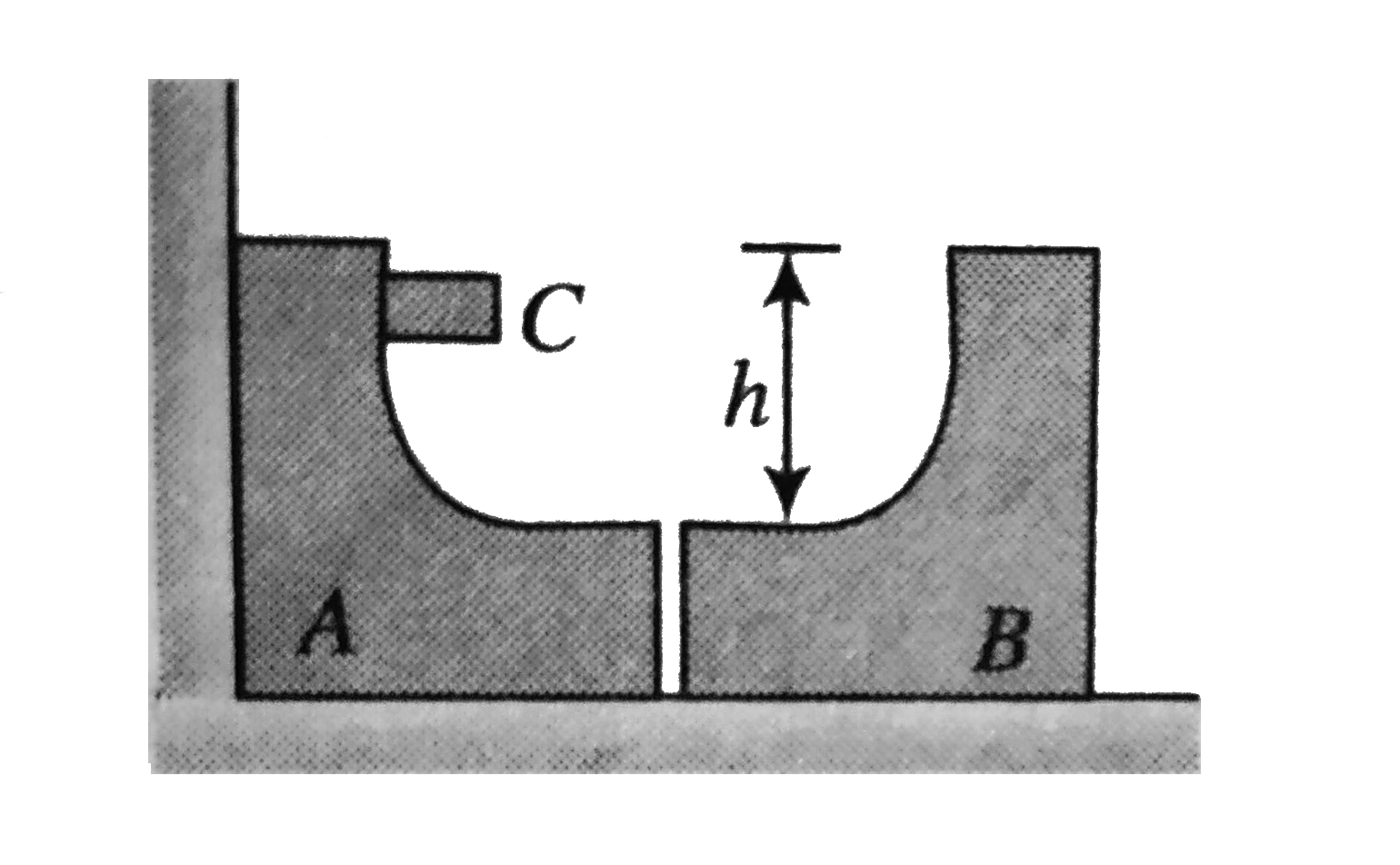
View SolutionA
View SolutionA stone at the end of
View SolutionBall A of mass m, after sliding from an inclined plane, strikes elastically another ball B of same mass at rest. Find the minimum heihgt h so that ball B just completes the circular motion of the surface at C. (All surfaces are smooth).
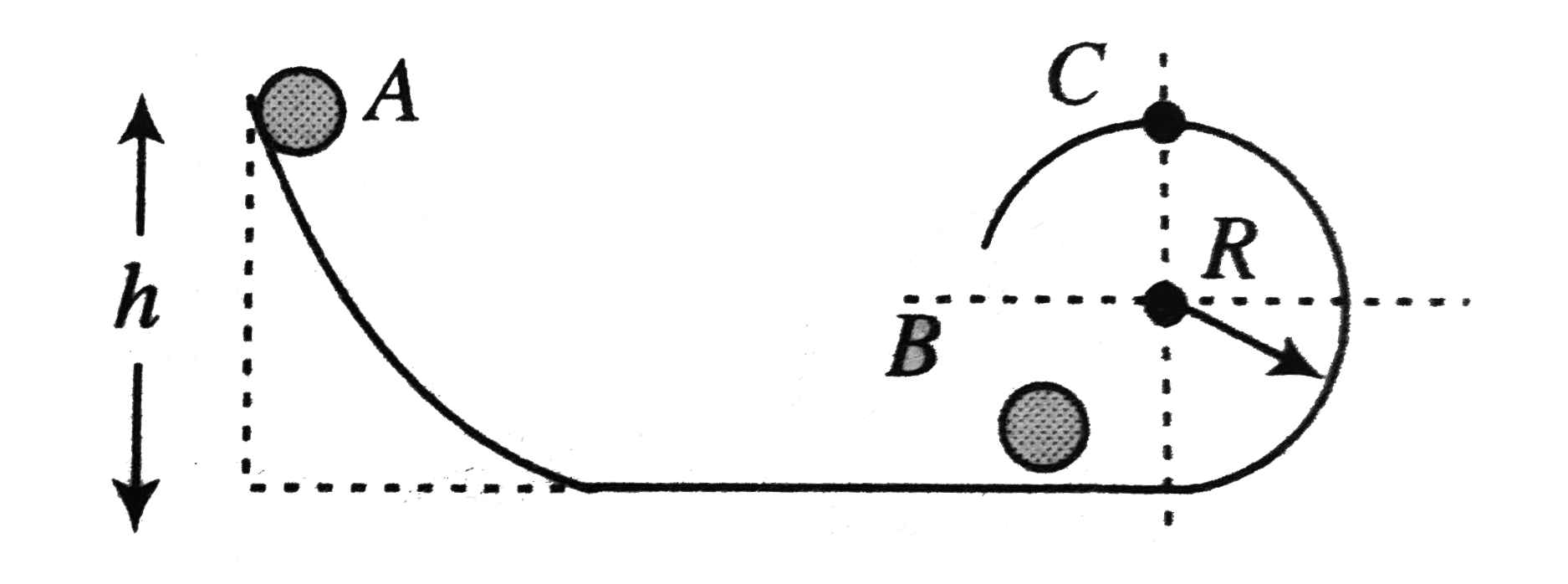
View SolutionA ball of mass
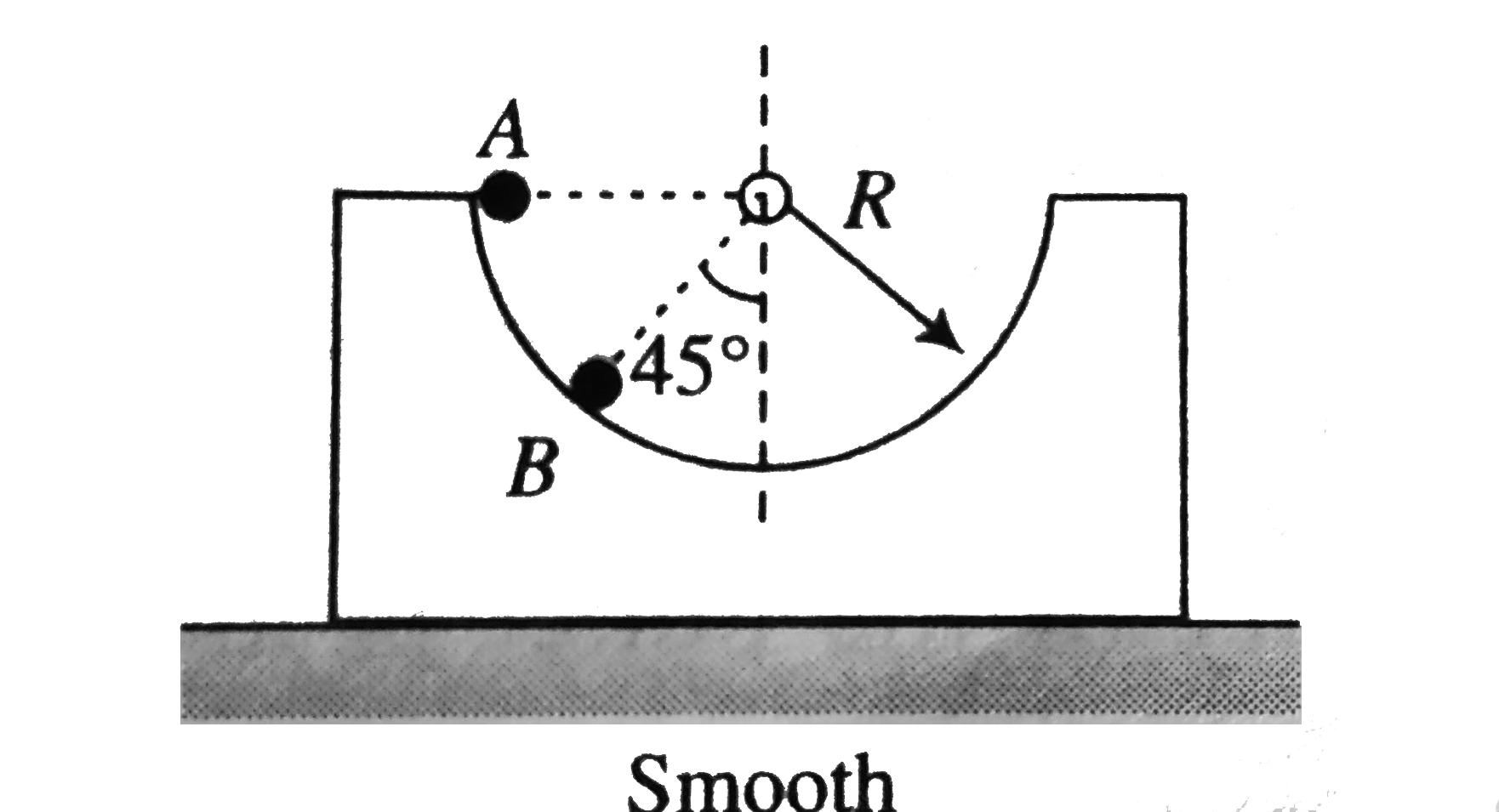
View SolutionA small sphere is given vertical velocity of magnitude
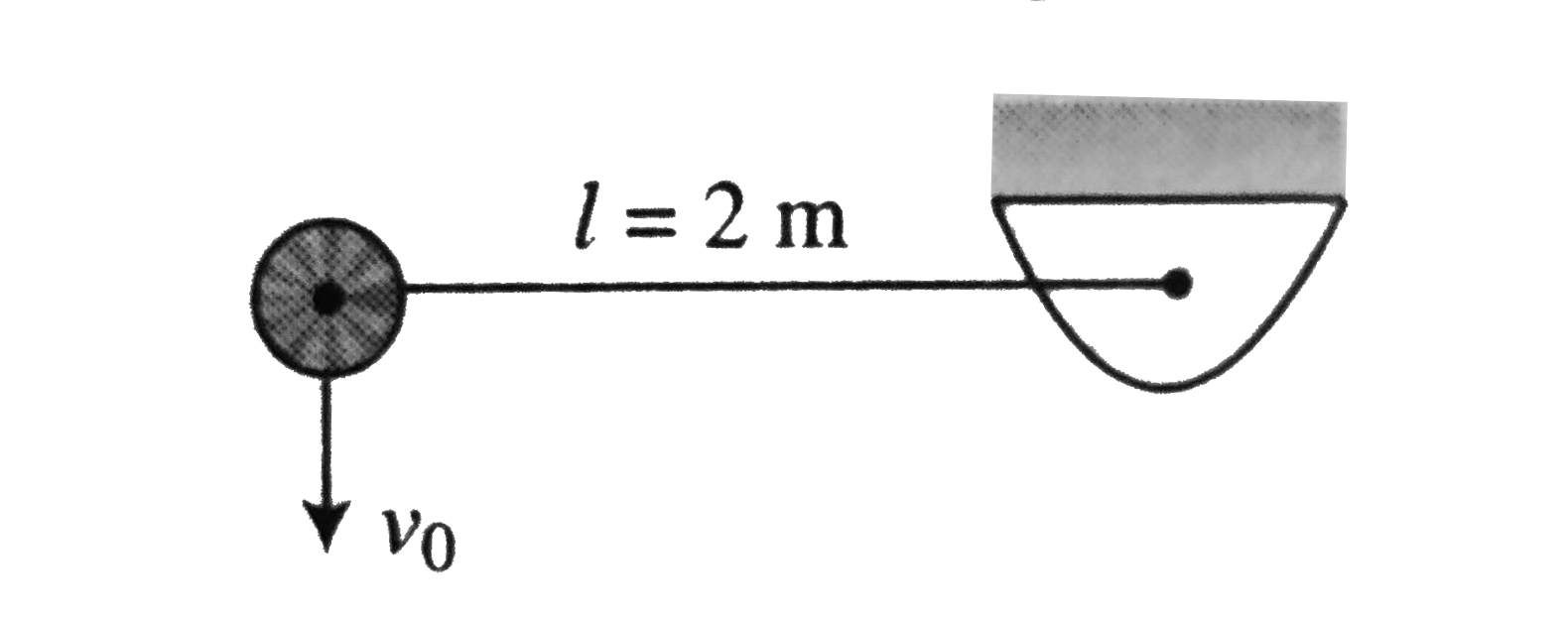
View SolutionIn the figure, block A is released from rest when the spring is its natural length for the block B of mass m to leave contact with the ground at some stage what should be the minimum mass of block A?
 .
.
View SolutionA block of mass
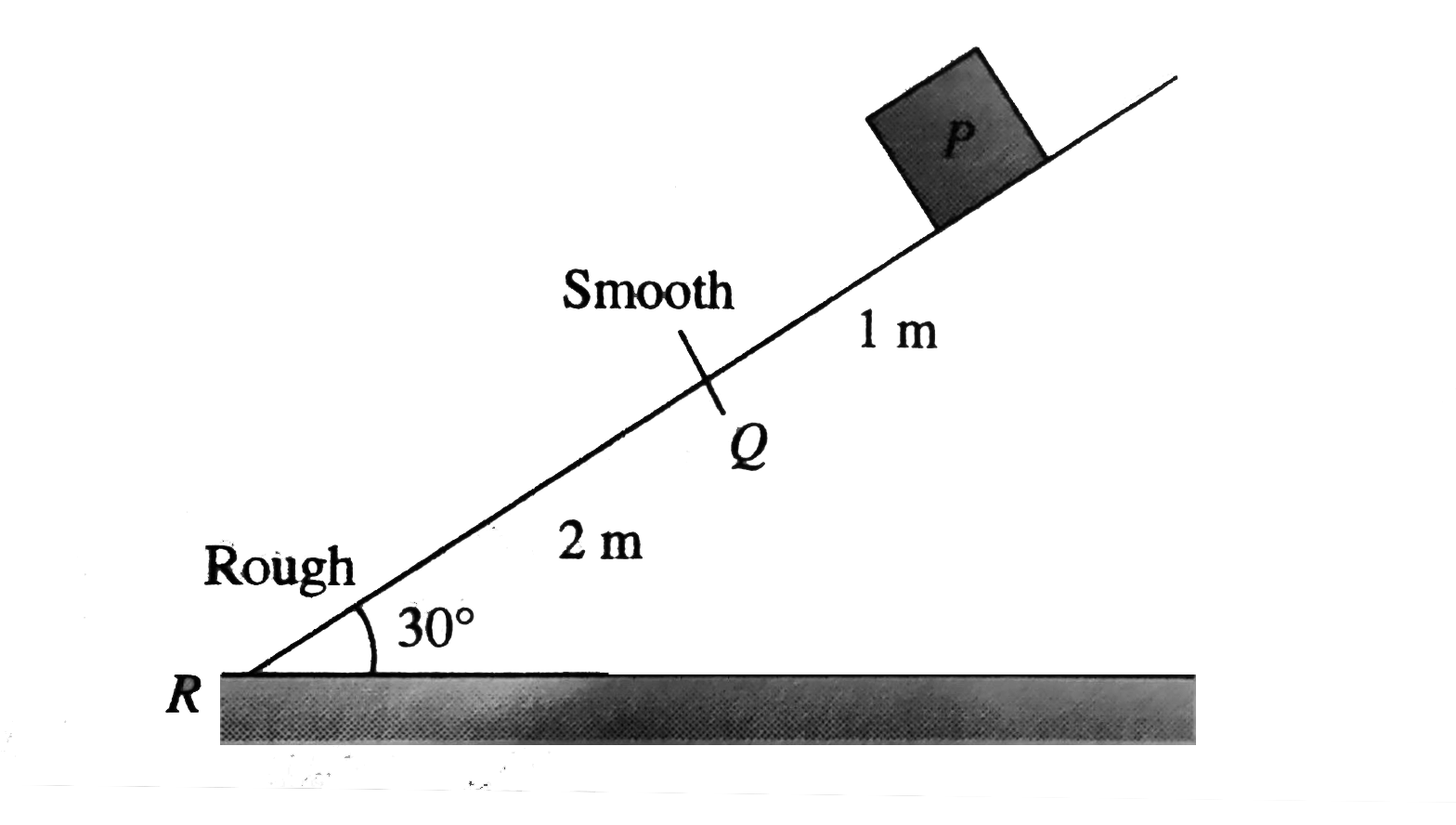
View Solution
Single Correct questions and complete solutions for chapter WORK, POWER & ENERGY of CENGAGE PHYSICS (HINGLISH) of Class 11