Complete Solutions to Example of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| CP SINGH | Example |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
When equal volumes of two substance are mixed, the specific gravity of the mixurie is 4. When equal weights of the same substance are mixed, the specific gravity of the mixture is 3. The soecufuc gravities of the two substance could be
View SolutionA cylinder vessel containing a liquid of density `rho` is closed by a smooth piston of mass `m` as shown. If atmospheric pressure is `P_0`, radius of cylinder is `r` and height of liquid is `h`. Find
(a) Pressure of liquid just below the piston
(b) force at bottom of cylinder.
 .
.
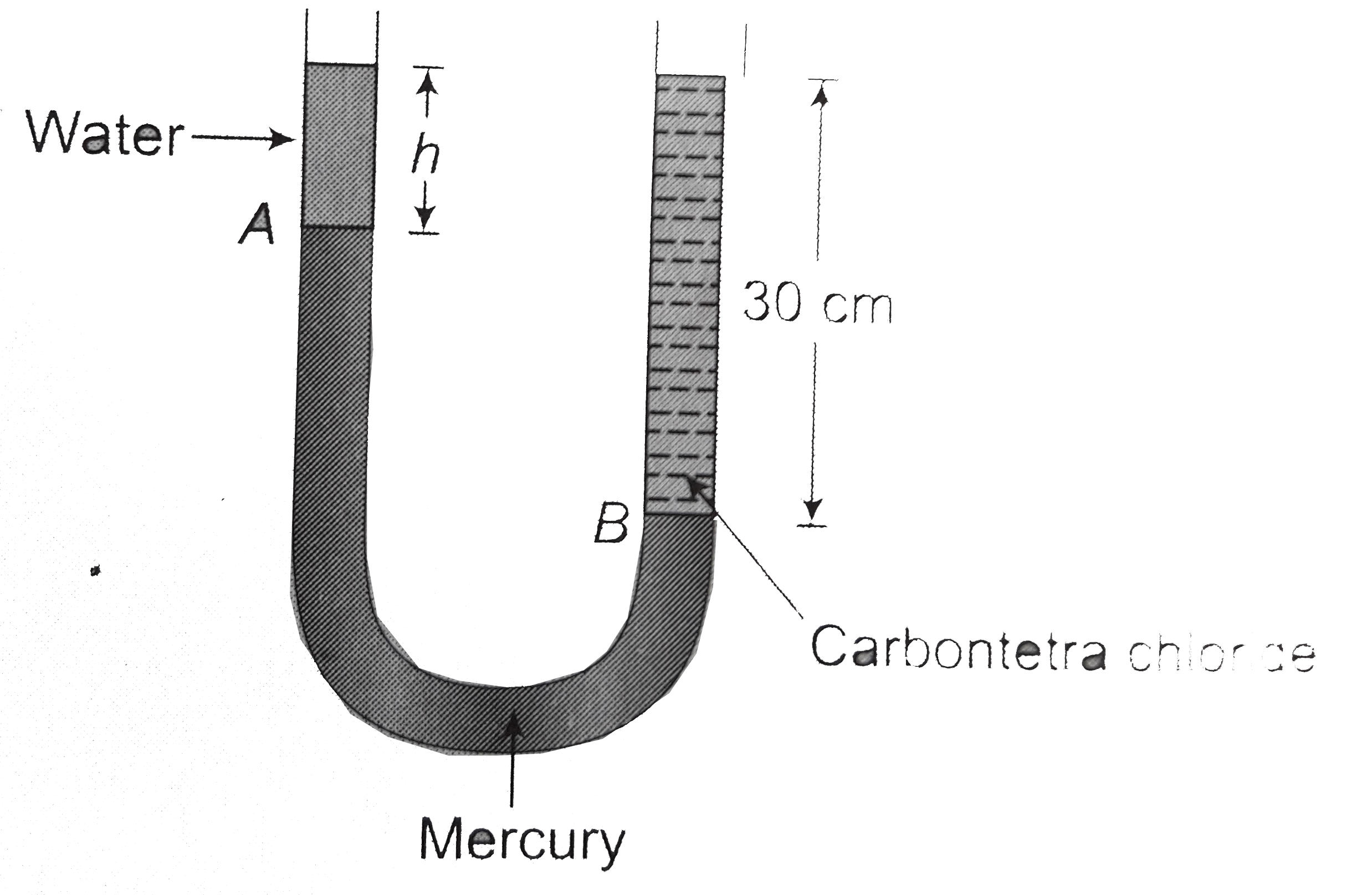
View SolutionConsider the situation shown in diagram. Determine `h`
`rho_omega = 1 g// c c. rho_m = 13.6 g//c c`
`rho_c = 1.6 g// c c`.
 .
.
View SolutionA glass full of water has a bottom of area `20 cm^(2)`, top of area `20 cm`, height `20 cm` and volume half a litre.
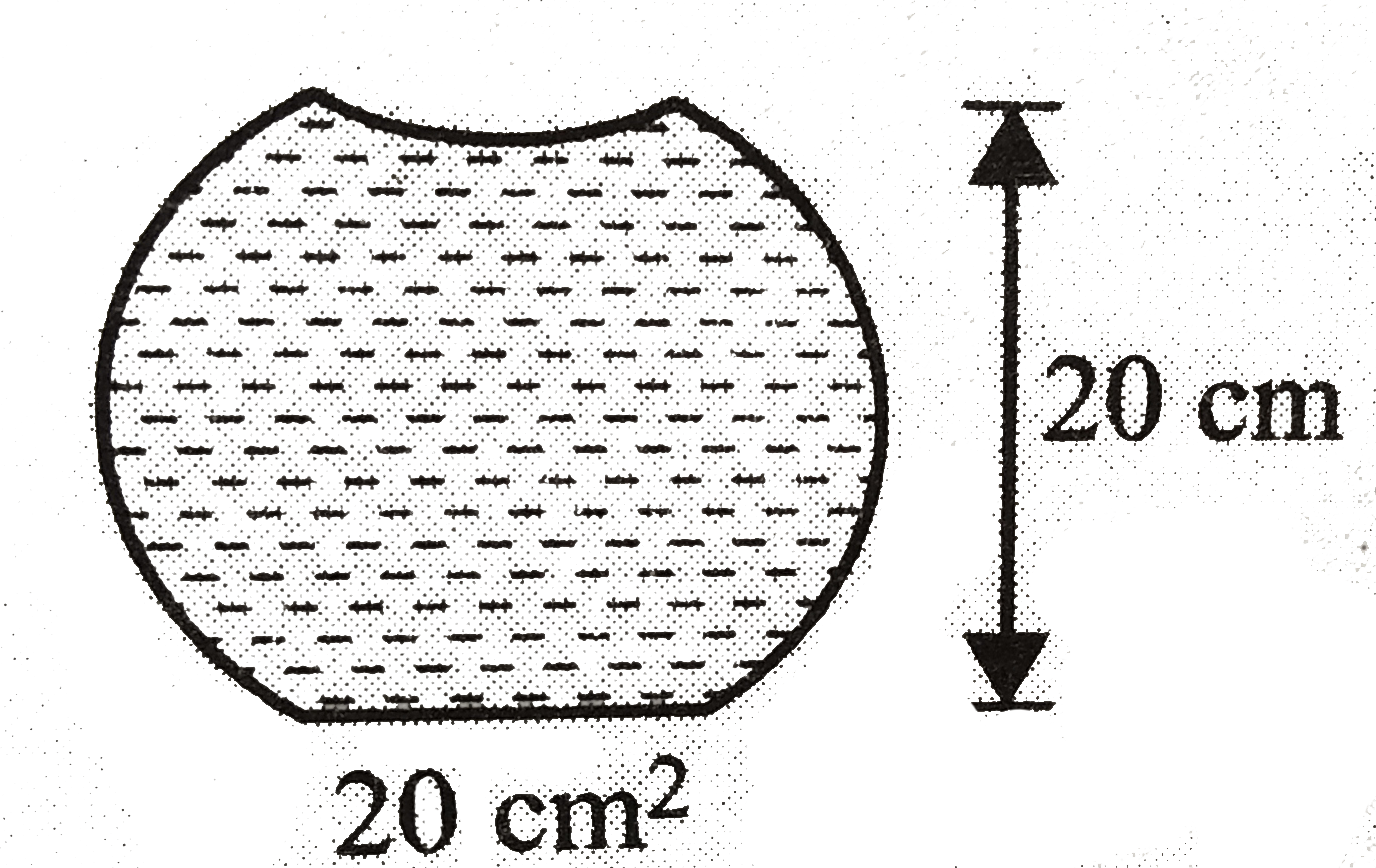
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the `v`, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure `= 1.0 xx 10^(5) N//m^(2)`. Density of water `= 1000 kg//m^(-3)` and `g = 10 m//s^(2)`
View SolutionSuppose the glass of the previous problem is covered by a jar and the air inside the jar is completely pumped out.
(a) What will be the answer to the problem ?
(b) Show that the answers do not change if a glass of different shape is used provided the height, the bottom area and the volume are unchanged.
View SolutionWhat is filled in a rectangular tank of size `3 m xx 2 m xx 1 m`.
(a) Find the total force exerted by the water on the bottom surface of the tank.
(b) Consider a vertical side of area `2 m xx 1 m`. Take a horizontal strip of width `delta x` metre in this side, situated at a depth of `x` metre from the surface of water. Find the force by the water on this strip.
( c) Find the torque of the force calculated in part (b) about the bottom edge of this side.
(d) Find the total force by the water on this side.
( e) Find the total torque by the water on the side about the bottom, edge. Neglect the atmospheric pressure and take `g = 10 m//s^2`.
View SolutionA bucket of water is suspended from a spring balance. What happens to reading of balance
(a) when a piece of stone suspended from a string is immersed in the water without touching the bucket
(b) when a piece of lead or cork is put in the water in the bucket.
View SolutionA beaker containing water is placed on the pan of a spring balance which shows a reading of `W_0`. A lump of sugar of mass `m` and volume `v` is now suspended by a thread (from an independent support). How will the reading change as time passes on ?
View SolutionA boat floating in a water tank is carrying a number of large stones. If the stones are unloaded into water, what will happen to the water level?
View SolutionA solid of density `sigma` floats in a liquid of density `rho`. What will happen to level of liquid if solid melts ?
View SolutionA piece of ice floating in a vessel filled with water. As the ice piece melts, what happens to the water level if
(a) (i) ice melts and (ii) ice piece contains an air bubble
(b) ice piece contains (i) a lead piece and (ii) a cork piece.
View Solution(a) An ornament weighting `36 g` in air, weights only `34 g` in water. Assuming that some copper is mixed with gold to prepare the ornament, find the amount of copper in it. Specific gravity of gold is `19.3` and that of copper is `8.9`.
(b) Refer to the previous problem. Suppose, the goldsmith argues that he has not mixed copper or any other material with gold, rather some cavities might have been left inside the ornament. Calculate the volume of the cavities left that will allow the weights given in that problem.
View SolutionAn ice cube floats in water. What percentage of volume is outside water. Density of water `= 1g// c c`, density of ice `= 0.9 g// c c`.
View SolutionA solid ball of density half that of water falls freely under gravity from a height of `20 m` and then enters water. Up to what depth will the ball go ? How much time will it take to come again to the wate surface ? Neglect air resistance and viscosity effect in water.
View SolutionA cubical block of wood weighing `200 g` has a lead piece fastened underneath. Find the mass of the lead pieces which will just allow the block to float in water. Specific gravity of wood is `0.8` and that of lead is `11.3`.
(b) Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA cube ofice of edge 4 cm is placed in an empty cylindrical glass of inner diameter 6 cm. Assume that the ice melts uniformly from each side so that it always retains its cubical shape. Remembering that ice lighter than water, finding the length of the edge of the ice cube at the instant it just leaves contact with the bottom of the glass.
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle `theta` that the plank makes with the vertical in the equilibrium position. (Exclude the case `theta=theta^@`)

View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =`800 kgm^-3` and spring constant of the spring `=50Nm^-1 Take g=10ms^-2`.
 ,
,
View SolutionA container of a large uniform cross-sectional area `A` resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities `d` and `2d`, each of height `H//2` as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length `L(L lt (H)/(2))`, cross-sectional area `A//5` is immersed such that it floats with its axis vertical of the liquid-liquid interface with length `L//4` denser liquid. Determine
(a) density `D` of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure `= P_0`).
 .
.
View SolutionA solid sphere of mass `m = 2 kg` and specific gravity `s = 0.5` is held stationary relative to a tank filled with water. The tank is accelerating upward with acceleration `2 m//s^2`. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank.
(Density of water `= 1000 kg m^-3, g = 10 ms^-2`).
 .
.
View SolutionA wooden stick of length `L`, radius `R` and density `rho` has a small metal piece of mass `m` ( of negligible volume) attached to its one end. Find the minimum value for the mass `m` (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density `sigma(gtrho)`.
View SolutionA solid sphere of radius `R` is floating in a liquid of density `sigma` with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
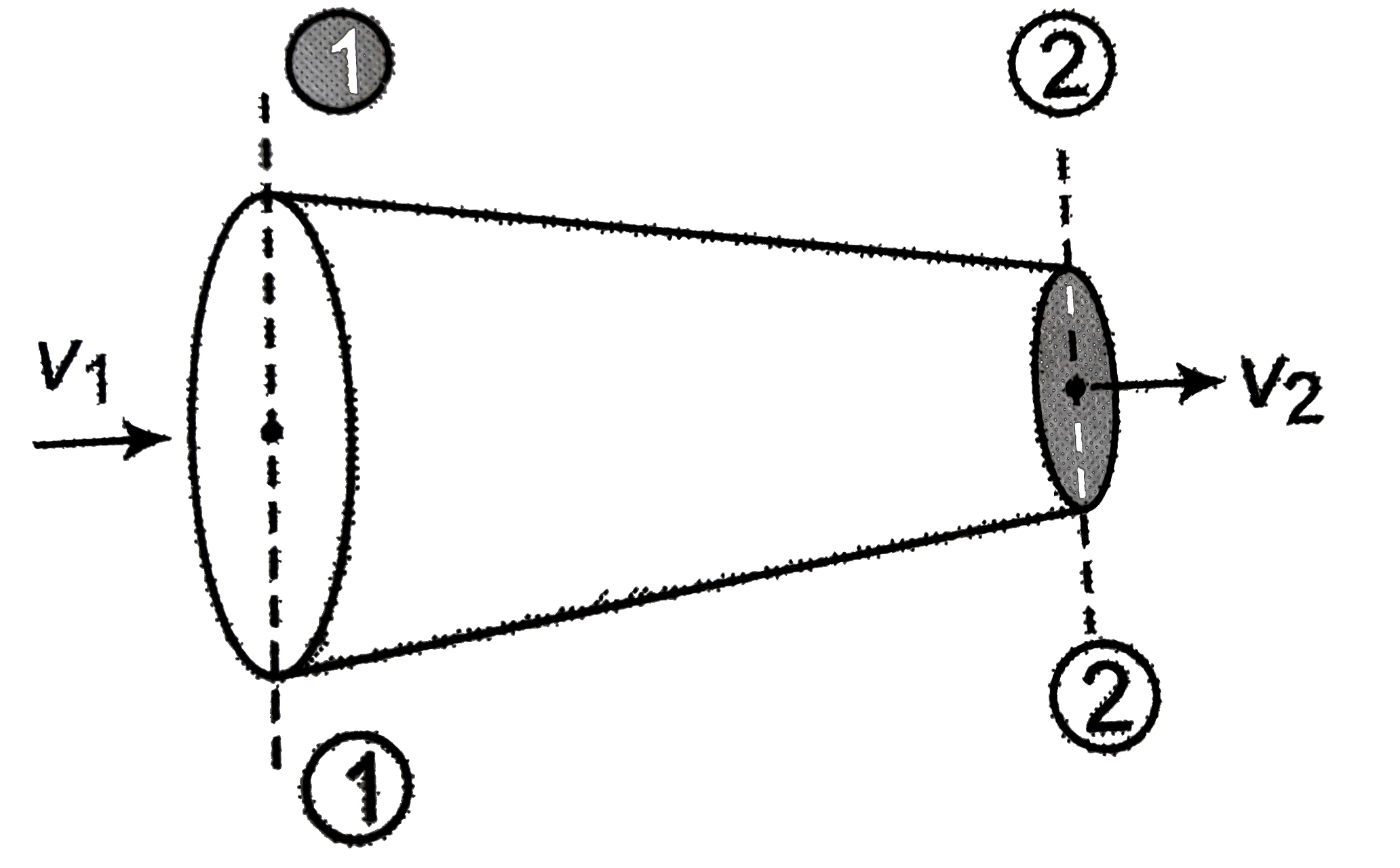
View SolutionA liquid of density `800 kg//m^3` flowing steadily in a tube of varying cross-section. If area of cross-section at `A` is `4 cm^2` and at `B` is `2 cm^2`. If speed of liquid at `A` is `10 cm//s`, calculate
(i) the rate of flow
(ii) the difference in pressures at `A` and `B`.
View SolutionWater is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is `4 xx 10^4 N//m^2` at a point where cross-section is `0.02 m^2` and velocity of flow is `2 m//s`. What is the pressure at a point where cross-section reduces to `0.01 m^2` ?
 .
.
View SolutionAir is streaming past a horizontal air plane wing such that its speed is `120 ms^-1` over the upper surface and `90 ms^-1` at the lower surface. If the density of air is `1.3 kg m^-3`m find the difference in pressure between the top and bottom of the wing. If the wing is `10 m` long and has an average width of `2 m`, calculate the gross lift of the wing.
View SolutionWater is flowing continuously from a tap having an internal diameter `8xx10^(-3)`m. The water velocity as it leves the tap is `0.4 ms^(-1)`. The diameter of the water stream at a distance `2xx10^(-1)`m below the tap is close to `(g=10m//s^(2))`
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are `4cm^2 and 2cm^2` respectively, find the rate of flow of water across any section.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are `5cm^2 and 2cm^2` respectively. The rate of flow of water through the tube is `500 cm^3s^-1` . Find the difference of mercury levels in the U-tube.

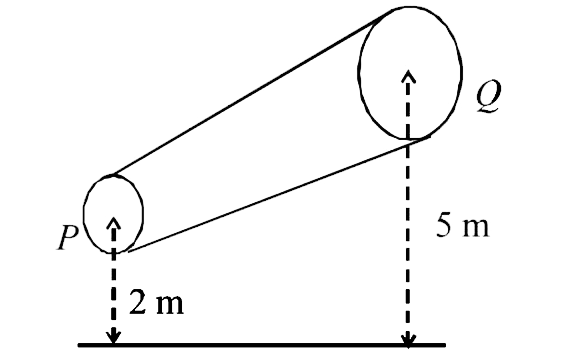
View SolutionA non-viscous liquid of constant density `1000kg//m^3` flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively `4xx10^-3m^2` and `8xx10^-3m^2`. The velocity of the liquid at point P is `1m//s`. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
View SolutionWater stands at a depth `H` in a tank whose side walls are vertical. A hole is made on one of the walls at a depth `h` below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor and for what value of `h` this range is maximum ? What is the maximum possible range ?
View SolutionA cylindrical tank `1 m` in radius rests on a platform `5 m` high. Initially the tank is filled with water to a height of `5 m`. A plug whose area is `10 ^-4 m^2`, is removed from an orifice on the side of the tank at the bottom. Calculate the following :
(a) Initial speed with which the water flows from the orifice.
(b) Initial speed with which the water strikes the ground,
( c) Time taken to empty the tank to half its original value.
View SolutionThe density of liquid contained in the tank of area `0.5 m^2` is `1200 kg//m^2`. It has a hole of area `1 cm^2` near the bottom. A load of `30 g` is applied on the liquid at the top. Find the velocity of efflux when the height of liquid level is `75 cm` above the bottom. Take `g = 10 m//s^2`.
View SolutionConsider a horizontally oriented syringe containing water located of a height of `1.25 m` above the ground. The diameter of plunger is `8 mm` and the diameter if the nozzle is `2 mm`. The plunger is pushed with a constant speed of `0.25 m//s`. Find the horizontal range of water stream on the ground. Take `g = 10 m//s^2`.
 .
.
View SolutionA cylindrical tank has a small hole at bottom. At `t = 0`, a tap starts to supply water into the tank at a constant rate `beta m^3//s`.
(a) Find the maximum level of water `H_(max)` in the tank ?
(b) At what time level of water becomes `h(h lt H_(max))` Given `a` , area of hole, `A` : area of tank.
View SolutionA container of large uniform cross sectional area `A`, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density `d` and `2d`, each of height `H/2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`. A tiny hole of area `(s(sltltA)` is punched on the vertical side of the container at a height `h(hltH/2)`. Determine

a.the initial speed of efflux of the liquid at the hole
b. the horizontal disance `x` travelled by the liquid initially
c. the height `h_m` at which at the hole should be punched so that the liquid travels the maximum distance `x_(m)` initially. also calculate `x_(m)` (neglect air resistance in calculations).
View SolutionOn the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross section area a. The height difference between them is equal to `h`. Find the resultant force of reaction of water flowing out of vessel.
View SolutionA cylindrical vessel filled with water upto a height of `2m` stands on horizontal plane. The side wall of the vessel has a pugged circular hole touching the bottom. If the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed is `(x)/(10sqrt(pi))` meter then `x` will be (if the coefficient of frication between the bottom of the vessel and the plane is `0.4` and total mass of water plus vessel is `100 kg`.)
View SolutionThe fresh water behind a reservoir dam is `15 m` deep. A horizontal pipe `4.0 cm` in diameter passes through the dam `6.0 m` below the water surface as shown in the figure. A plug secures the pipe opening :
(a) Find the friction force between the plug and the pipe wall.
(b) The plug is removed. What volume of water flows out of the pipe in `3.0` hour ? Assume that reservoir is large.
 .
.
View SolutionA liquid of density `rho` is in a vessel rotating with angular velocity `omega` as shown in figure. If `P_0` is the atmospheric pressure, find pressure at a radial distance `r` from the axis.
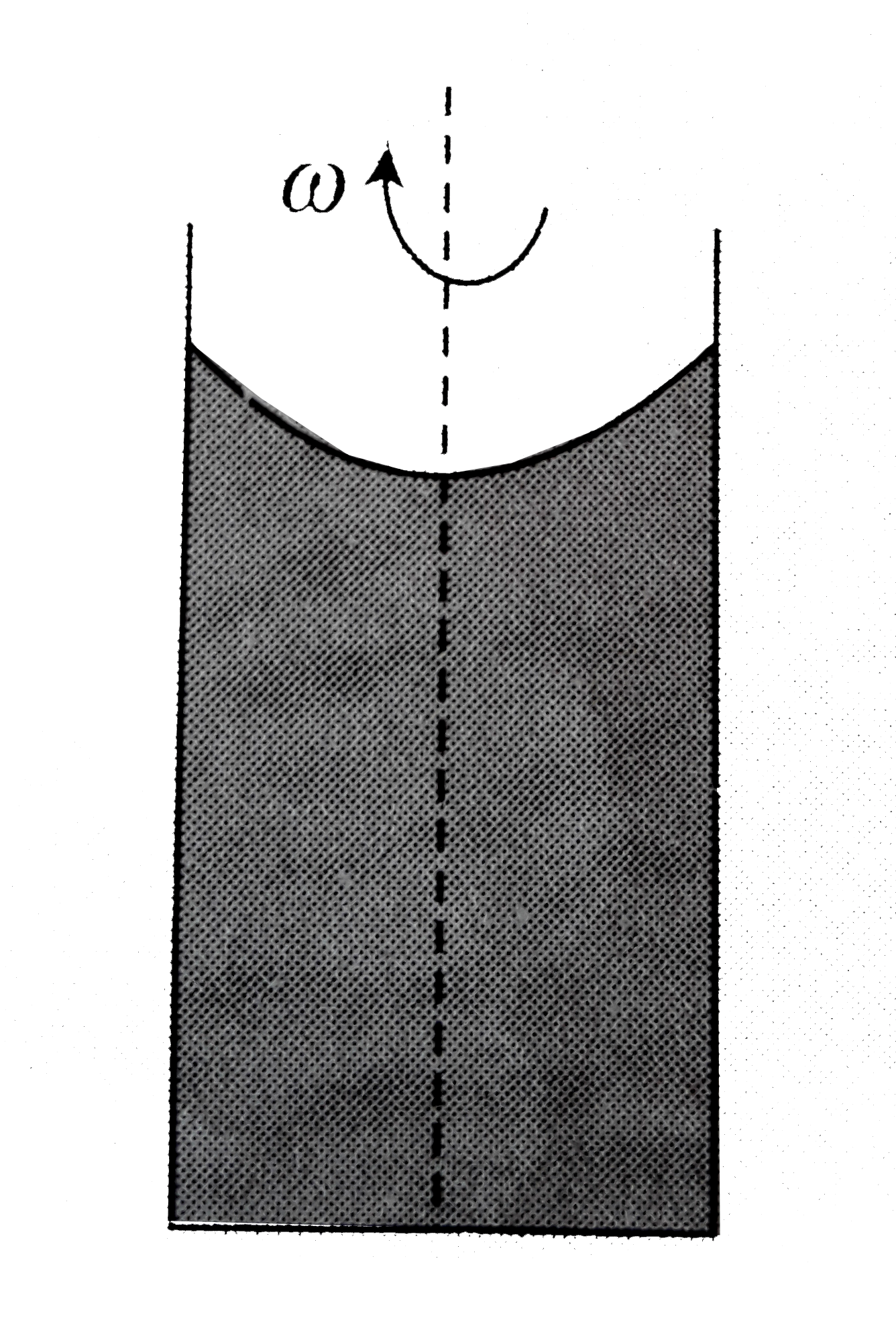 .
.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is ` 0.05 m` and the speed of rotation is `2 rev//s`, find difference in the height of the liquid at the centre of the vessel and its sides.
View Solution
Example questions and complete solutions for chapter FLUID MECHANICS of CP SINGH PHYSICS (HINGLISH) of Class 11